冷原子陀螺仪三维磁场系统的容差设计

李 攀，刘元正，王继良

（西安飞行自动控制研究所，西安 710065）

冷原子陀螺仪三维磁场系统的容差设计

李 攀，刘元正，王继良

（西安飞行自动控制研究所，西安 710065）

磁场系统作为磁光阱的重要组成部分，在高精度冷原子陀螺仪中占有极其重要的地位。随着陀螺体积的不断减小和集成度的不断提高，磁场系统的制造和装调误差对陀螺性能的影响不断增大。这些误差会引起磁场零点漂移和磁场梯度变化，降低捕获效率和原子团的质量，从而影响陀螺性能。从三维磁光阱磁场分布的理论分析出发，结合数学建模和计算机仿真，对三维磁场系统的主要制造和装调误差对磁场的影响进行了分析和比较，并基于预设阈值利用试验设计和数学回归对关键制造和装调参数设计了合理的容差限，为小型化冷原子陀螺仪三维磁场系统的设计和制造提供了理论依据。

冷原子陀螺仪；磁光阱；磁场系统；容差设计

冷原子陀螺是目前已知的理论精度最高的惯性敏感器，在同等干涉环路面积下，其精度可达激光陀螺的～1011倍[1]，纯惯性导航的理论精度达到5 m/h，可以独立完成长时间、远航程的导航任务[2]。2010年，美国 Draper实验室在对远期陀螺技术应用的展望中预测，2020年左右冷原子陀螺将占据超高精度导航领域市场（10−6(°)/h）[3]。美国空军已将冷原子陀螺作为2010～2030年无GPS辅助惯性导航系统唯一惯性传感器[4]。

由于冷原子陀螺具有超高性能和巨大潜力，将对惯性导航领域产生重大影响，世界各国知名机构均投入大量人力物力从事相关研究工作，以期占据原子陀螺技术的至高点，实现惯性导航领导的绝对技术优势和领先地位[5-10]。随着冷原子技术的逐渐成熟，困扰冷原子导航传感器实际应用的稳定性、体积和功耗问题正在逐步得到解决。2008年，美国斯坦福大学利用微晶玻璃真空腔和 π/2-π-π-π/2原子干涉构型显著减小了陀螺体积，形成了全球首款可移动的冷原子陀螺仪[11]；2011年，美国AOSense公司发布了全球首款原子光学传感器商品——商用冷原子重力梯度仪[12]，噪声小于 1×10−6g/Hz1/2。这些成果标志着冷原子惯性传感器已经开始向工程化、小型化迅速发展。

随着冷原子陀螺仪体积的不断减小和集成度的不断提高，制造和装调误差对陀螺性能的影响不断增大。比如，由于随着陀螺体积减小，三维磁光阱的可调节范围也不断减小，此时磁光阱线圈的制造和装调误差将更易引起三维磁光阱性能变化，降低捕获率及捕获原子团的质量。所以，开展容差设计研究、设计合理的容差限对于逐渐走向小型化、工程化的冷原子陀螺仪很有必要。

本文从三维磁光阱磁场分布的理论分析出发，结合数学建模和计算机仿真，对三维磁光阱线圈的主要制造和装调误差对磁场的影响进行了分析和比较，根据预设的阈值设计了合理的容差限，为小型化冷原子陀螺仪三维磁场系统的设计和制造提供了理论依据。

1 三维磁场系统理论分析

1.1 载流环形线圈的磁场

结合图1所示，根据毕奥-萨伐尔-拉普拉斯定律，任一电流元Idl在点P形成的磁场可以表示为

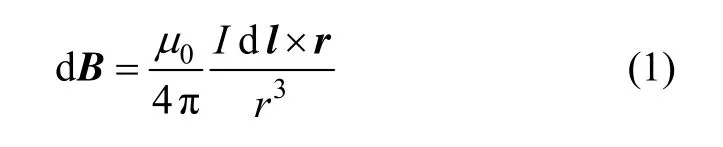
式中，r为元电荷指向点P的矢量，μ0为真空电导率。

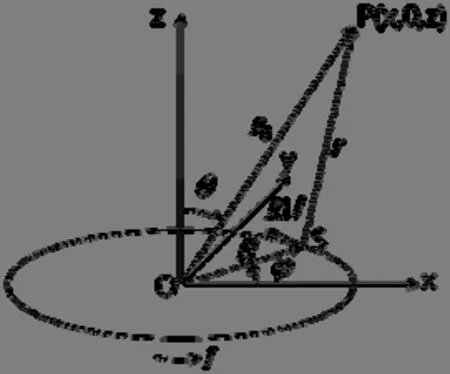
图1 环形电流磁场Fig.1 Ring current magnetic field

由于线圈具有轴对称特性，可将点P放在xz平面上以减少计算步骤。考虑位于S点的电流元Idl，OS与x轴的夹角为φ，则有：

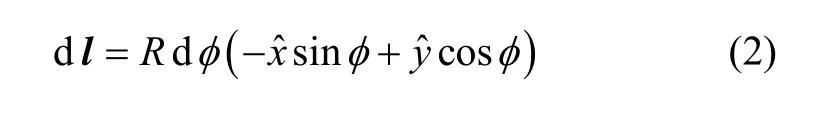
由图1可知，

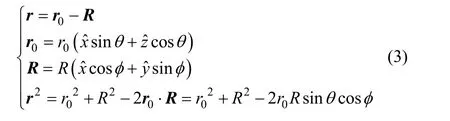
将式(2)(3)代入式(1)可得：

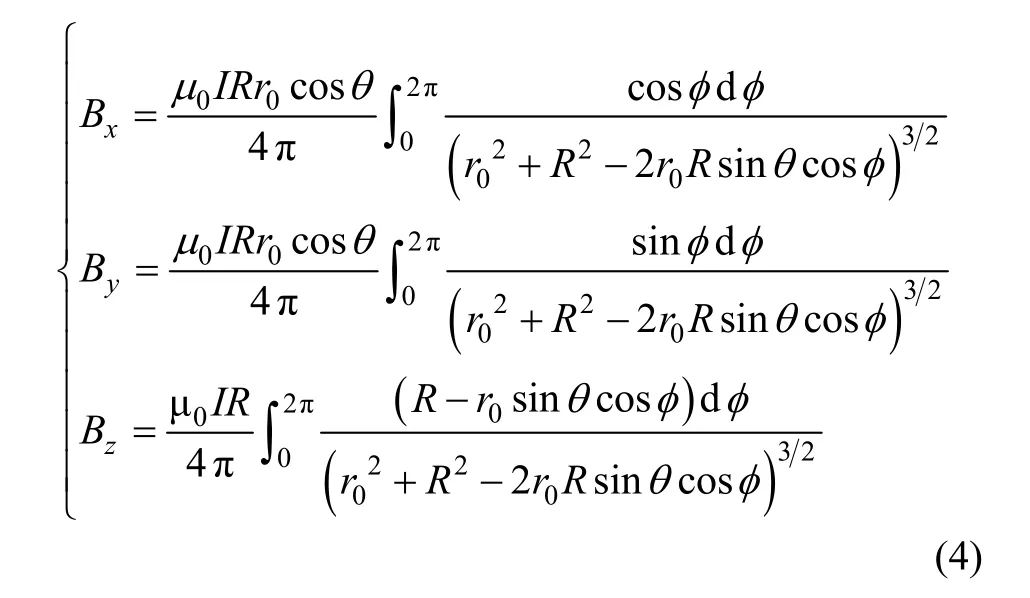
化简，可得：

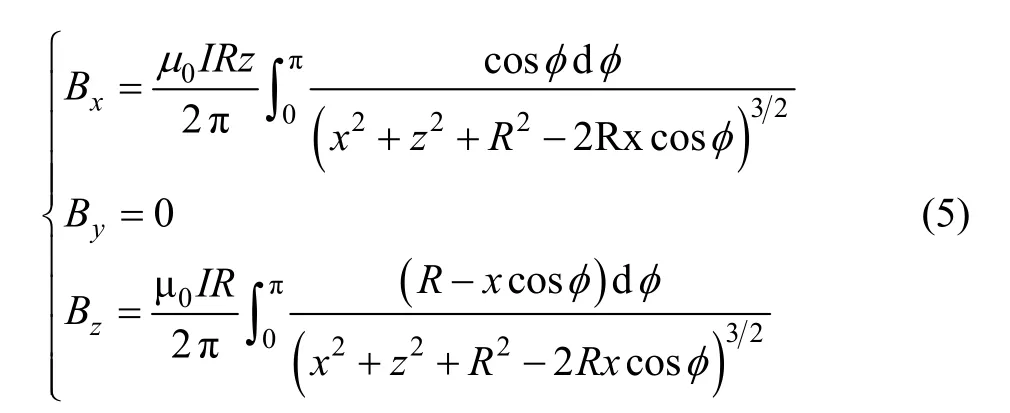
1.2 反亥姆霍兹线圈形成的磁场

现考虑反亥姆霍兹线圈，它由一对间距L的环形线圈构成，两个线圈的载流方向相反，如图2所示。

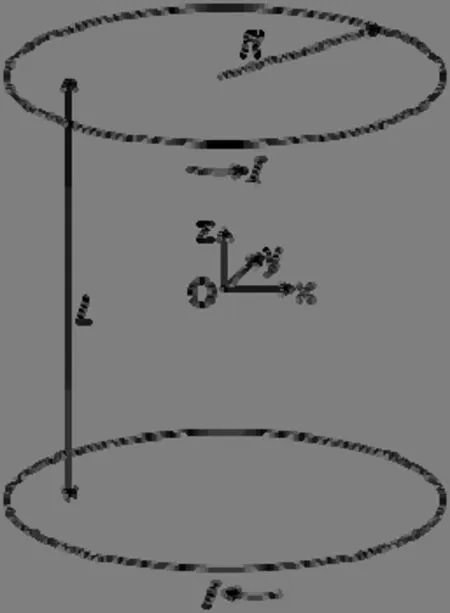
图2 反亥姆霍兹线圈Fig.2 Anti-Helmholtz coils

以两个线圈中心为坐标原点建立坐标系，那么沿x轴和z轴的磁感应强度可以表示为两个线圈的叠加：

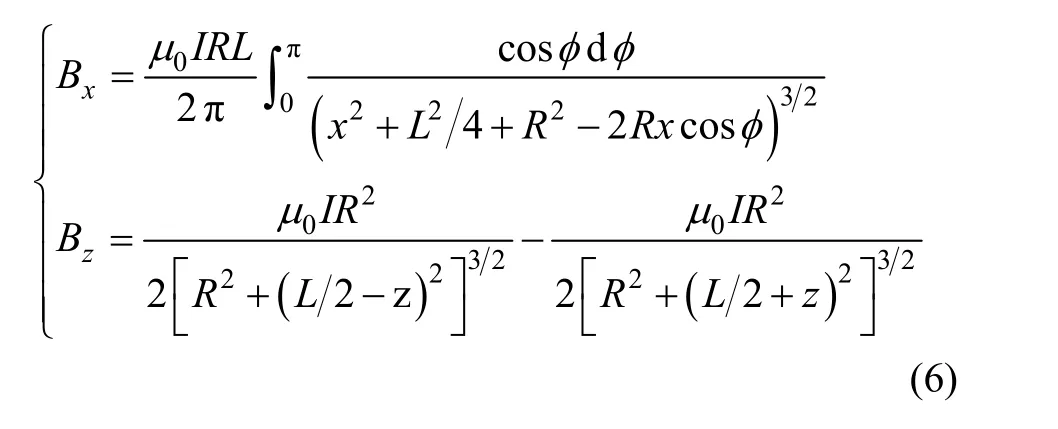
多重反亥姆霍兹线圈可以表示为多组反亥姆霍兹线圈的叠加。设d为导线直径，n1为轴向磁场线圈匝数，n2为径向磁场匝数，R1、R2为线圈内、外径，L0为线圈间距，那么沿x轴和z轴的磁感应强度可以表示为：

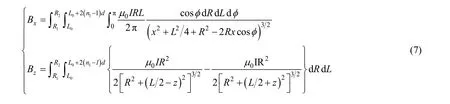
利用Matlab进行仿真计算，可以完成线圈设计（I=2 A，R1=47.5 mm，L0=54 mm，n1=12，n2=13，d=1 mm），并得到其轴向和径向磁场分布（图3）。

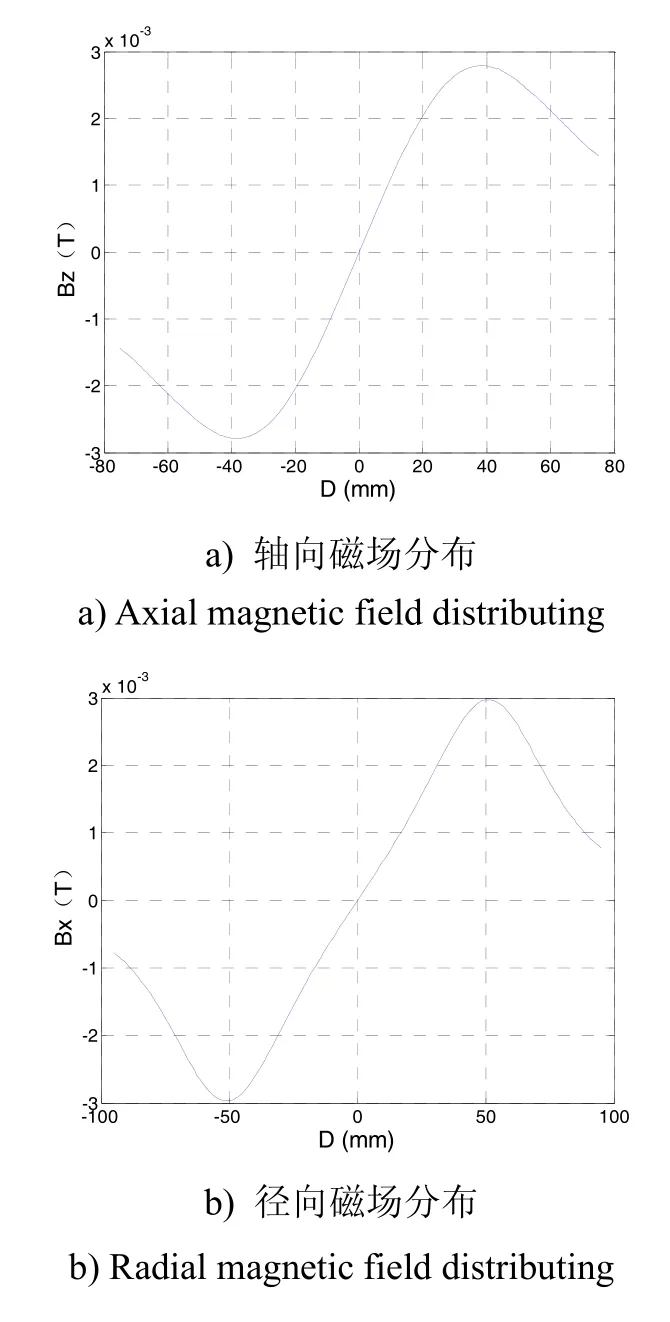
图3 轴向和径向磁场分布Fig.3 Axial and radial magnetic field distributing

图3中D为距磁场中心的距离，Bx、Bz分别为沿x轴和z轴的磁感应强度。考虑到陷俘光直径一般不超过20 mm，所以仅需考虑磁场中心±10 mm范围内的磁场梯度。对±10 mm范围内的磁场进行拟合，可以得到轴向磁场梯度dBz=0.1119 T/m 和径向磁场梯度dBx=dBy=0.0575 T/m，符合三维磁光阱轴向磁场梯度大于0.1 T/m的经验性要求。

2 误差分析

上述磁场设计仅考虑了理想状态，但在实际加工中往往存在着各种制造误差，主要包括：两线圈的对称轴不重合（简称同轴度误差）、两线圈定位面不平行（简称平行度误差）、两线圈匝数不相等（简称线圈不对称）以及线圈龙骨加工误差引起的两线圈内径不相等（简称内径不对称）等。这些误差或引起线圈移位，或引起线圈倾斜，会导致磁场零点漂移和磁场分布变化，所以必须确定这些误差的容差范围，并在设计指标中加以限定。

为统一模型，固定下线圈保持不变，制造误差均体现在上线圈上。利用Matlab在初始坐标系下分别计算线圈组合沿x、y、z轴的磁场分布，根据仿真结果确定磁场零点漂移Δ，然后以新的磁场零点建立坐标系，重新计算磁场分布。

控制阈值选择dBz≥0.1 T/m，磁场零点漂移Δ≤1 mm，以阈值点处的制造误差为容差设计提供参考。

2.1 同轴度误差C

使上线圈沿x轴移动以产生偏心误差C，得到磁场随偏心误差C的变化如图4所示。

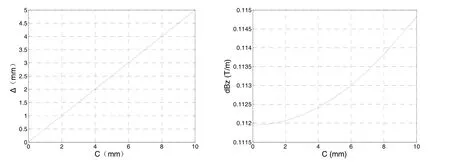
图4 同轴度误差对磁场的影响Fig.4 Effects of coaxiality error on magnetic field

磁场零点会沿着轴对称误差的方向移动，移动距离等于轴对称误差的一半；而磁场梯度随着偏心误差的增加而逐渐加大。考虑到控制阈值，C≤2 mm。

2.2 平行度误差θ

以上、下线圈的下底面作为定位面，绕x轴转动上线圈以产生平行度误差θ，得到的磁场变化如图5所示。

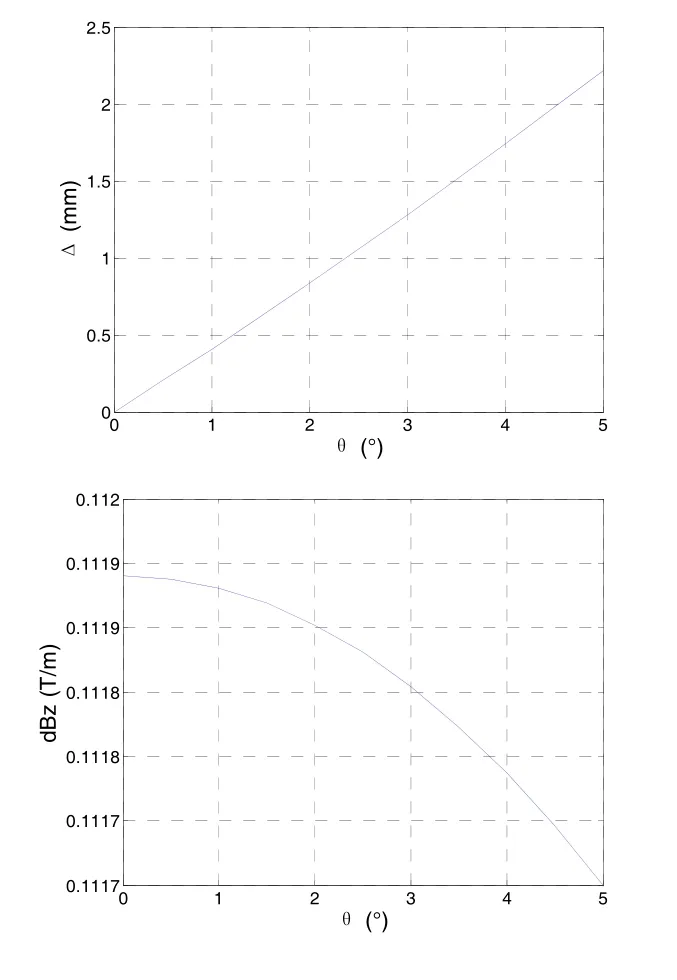
图5 平行度误差对磁场的影响Fig.5 Effects of parallelism error on magnetic field

磁场零点漂移随平行度误差近乎线性增加，主要沿x轴方向，y、z轴方向变化相对不明显；而磁场梯度随着偏心误差的增加而逐渐减小，但幅度不明显。考虑到控制阈值，θ≤2.375°。

2.3 线圈不对称a

定义线圈不对称指标a=ΔN/N，ΔN为上、下线圈的匝数差，N=n1·n2为下线圈的总匝数。减少上线圈匝数以形成线圈不对称，可以得到磁场与线圈不对称指标a之间的关系如图6所示。

线圈不对称会引起磁场零点在z轴方向移动，而在x、y轴方向则保持不变。从图 6中可以看出，线圈不对称会显著降低磁场质量，随着不对称加剧，零点位移增大，磁场梯度也迅速减小。考虑到控制阈值，当a＜0.052时满足Δ≤1 mm，dBz＞0.1 T/m。

通过对上、下线圈分别加不同电流可以使磁场零点沿z轴移动从而对线圈不对称进行补偿。如果上、下线圈所通的总电流保持一致，即使上、下线圈差别相对较大如a=0.1，此时磁场零点漂移仍满足控制指标Δ≈−0.2449 mm＜1 mm。

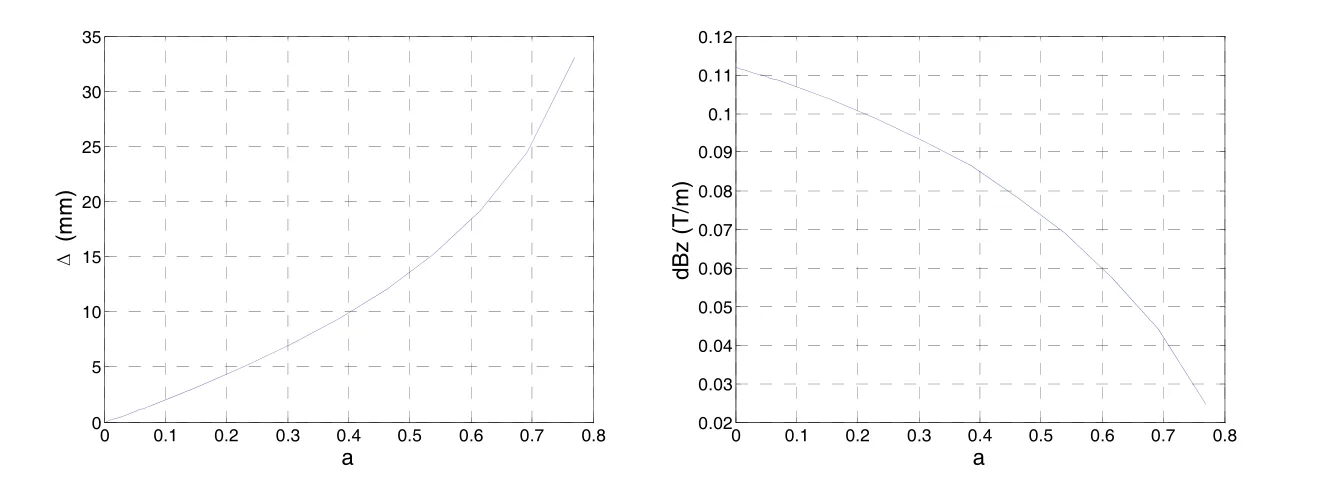
图6 线圈不对称误差对磁场的影响Fig.6 Effects of coils asymmetry on magnetic field

2.4 内径不对称

定义内径不对称指标b=ΔR/R，ΔR为上、下线圈的半径差。减小上线圈内径可以得到磁场与内径不对称b之间的关系如图7所示。

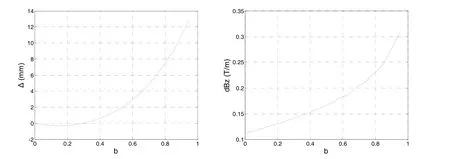
图7 内径不对称误差对磁场的影响Fig.7 Effects of inside diameter asymmetry on magnetic field

内径不对称会引起磁场零点在z轴方向移动，在x、y轴方向则保持不变。从图7中可以看出，当b≤0.44时，Δ＜1 mm；对于R=47.5 mm，这相当于超过13.5 mm的加工误差，几乎不大可能。有趣的是，图7中Δ在b≈0.293的位置又出现一个零点，即ΔR=13.92时磁场零点与ΔR=0时保持一致。拟合得到dBz=0.1399 T/m，也满足阈值控制指标。

3 容差设计

从上述分析可以看出，同轴度误差、平行度误差、线圈匝数不对称、线圈内径不对称都会对磁场产生影响，改变三维磁光阱的性能，所以必须在设计中加以限定。

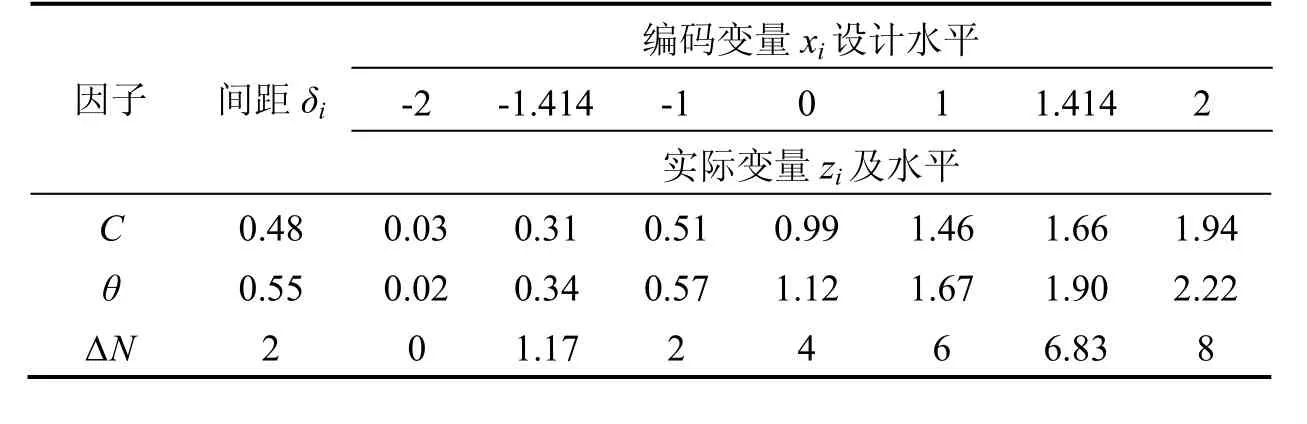
表1 最优近似饱和设计试验因子及水平Tab.1 Optimal approximation saturation design experimental factors and levels

由于各容差参数之间的单位、性质并不完全相同，对磁场参数的影响也不是简单的线性叠加，传统的等公差法、等精度法等容差设计方法并不完全适合。所以下文将采用回归分析的方法建立容差参数与磁场性能参数之间的回归关系，根据现有加工能力和各容差参数加工的难易程度，从中优选出合适的容差参数组合。

为降低计算量并提高回归精度，并考虑到使用简单的一次回归正交设计并不能得到满意的结果，故采用最优近似饱和设计进行二次回归。由于在常规加工条件下，内径不对称误差对磁场的影响可以忽略，故取同轴度C (mm)、平行度θ (°)和线圈匝数差ΔN作为三因子采用最优近似饱和设计（R311D）进行回归设计，各因子的编码自变量（xi）的编码水平j和实际自变量（zi）的实际水平如表1所示。表1中，-2水平代表常规条件下加工能达到的极限精度，对于车加工形成的C和θ，对应标准公差等级7，通过查表可以得到，而绕制的ΔN可以达到最小，即ΔN=0。+2水平代表其它两因子均取-2水平时满足控制指标的极值，可以通过计算得到。实施水平间距δi为：

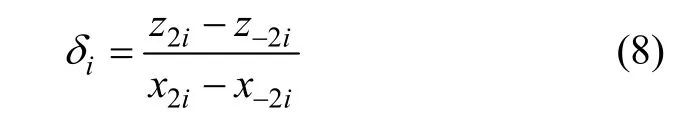
式中，xji和zji下标i代表编码，j代表设计水平。从而编码水平j对应的实际水平为：

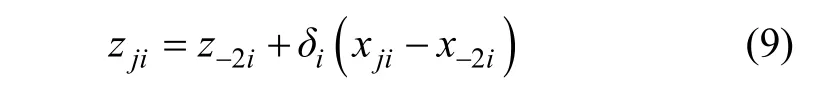
具体数值如表1所示。

使用Matlab进行计算，得到的结果如表2所示。

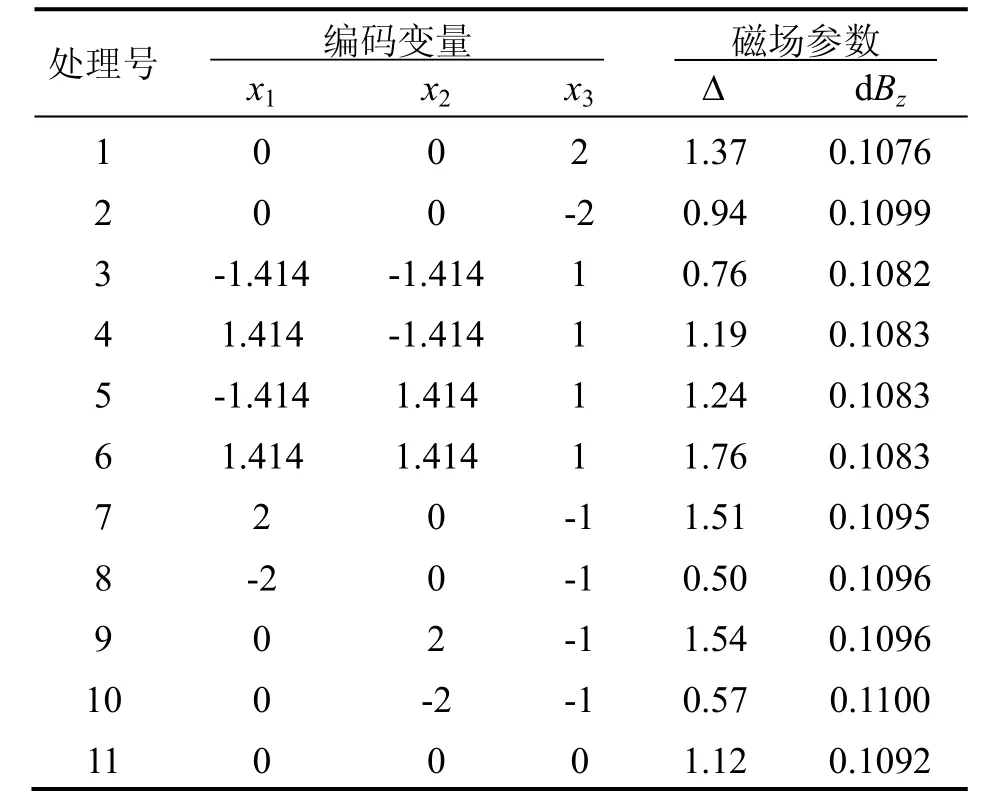
表2 试验方案及结果Tab.2 Experimental scheme and results

从表中可以看出，任意处理均满足 dBz≥0.1 T/m的控制指标，故只需计算Δ。

使用下列模型进行二次回归：

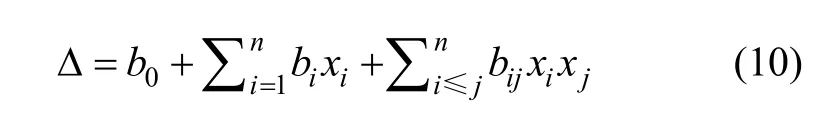
式中，n为自变量的数目，b0为回归方程的常数项，bi为一次项的偏回归系数，bij为二次项的偏回归系数。

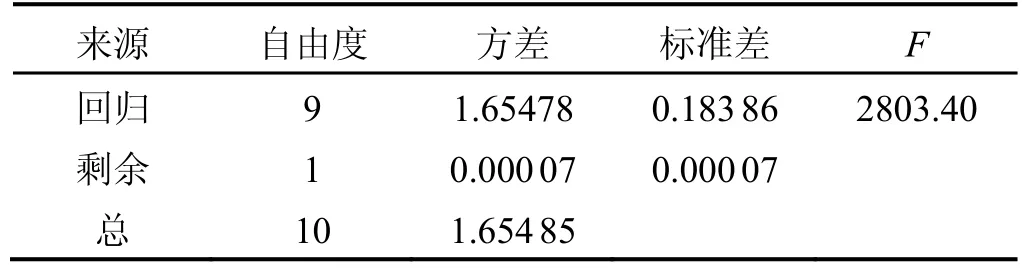
表3 试验方差分析Tab.3 Analysis of variance

使用Minitab进行数学回归。从方差分析表（表3）可以看出，回归达到显著水平（F＞F0.05(9,1)=241），回归方程的复相关系数Rsq=0.999 98；偏回归t检验中，b0、b1、b2达到极显著水平（p＜0.01），b3、b13、b23达到显著水平（p＜0.05），而其它系数未达到显著水平（p＞0.05），如表4所示。

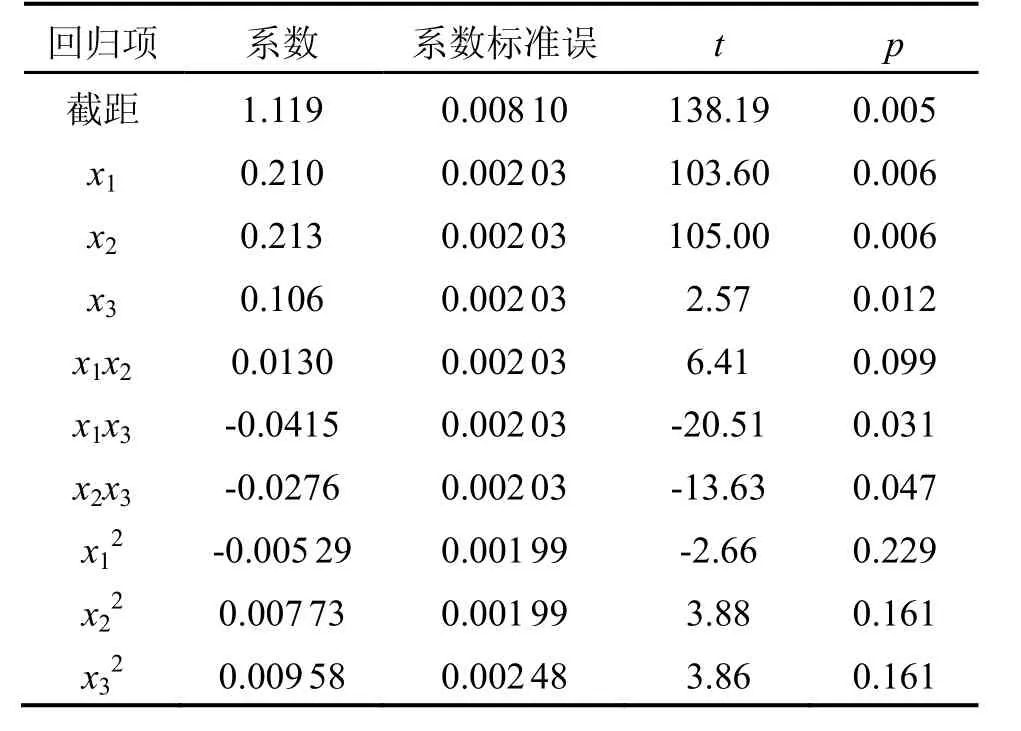
表4 偏回归系数b的t检验Tab.4 T test of partial regression coefficient b

回归方程为：

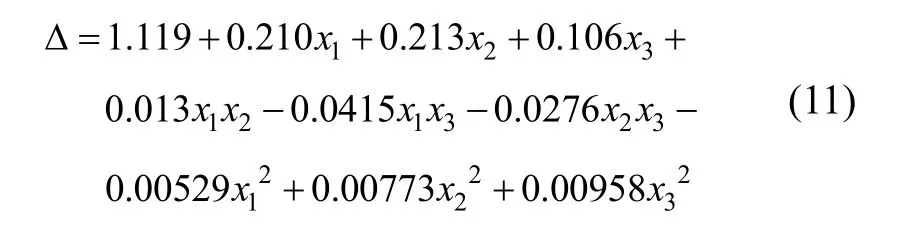
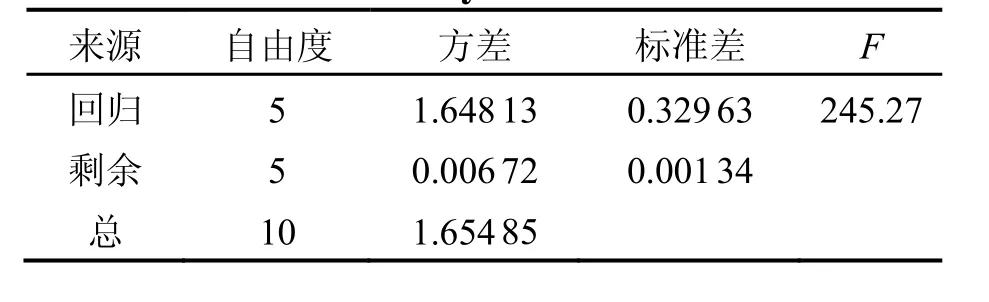
表5 试验方差分析Tab.5 Analysis of variance

将未达到显著水平的系数并入误差项重新进行回归。从表 5中可以看出，回归达到极显著水平（F＞F0.01(5, 5)=10.97），Rsq=0.996；偏回归t检验中，b0、b1、b2、b3、b13达到极显著水平（p＜0.01），b23达到显著水平（p＜0.05），如表6所示。

回归方程为：

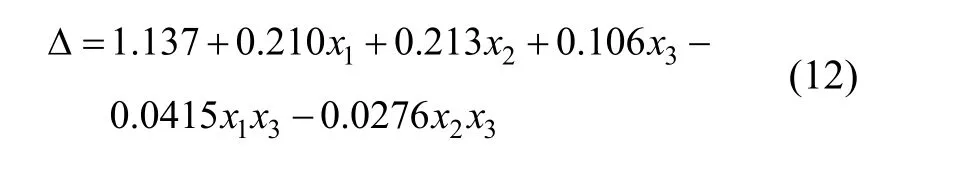
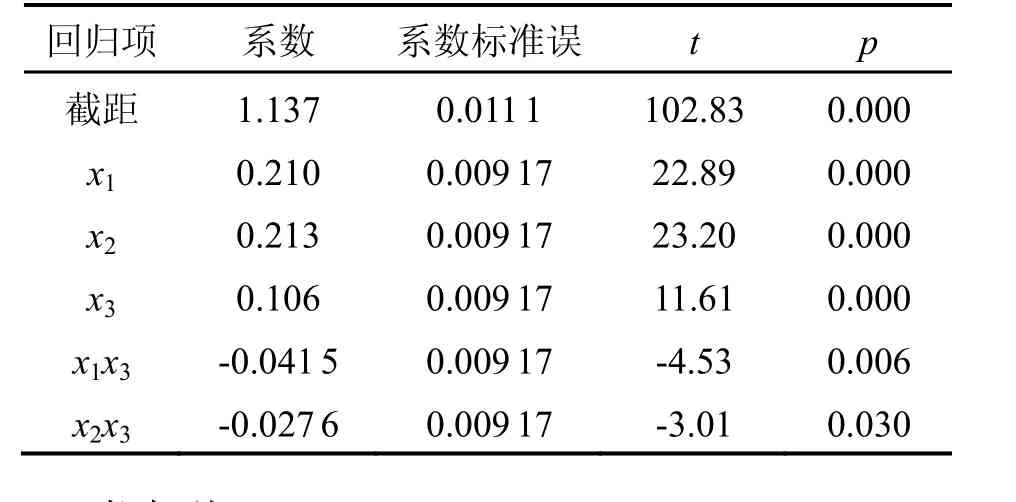
表6 偏回归系数b的t检验Tab.6 T test of partial regression coefficient b

考虑到

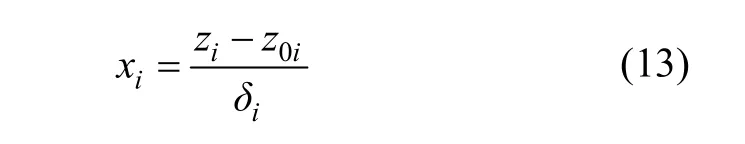
可得

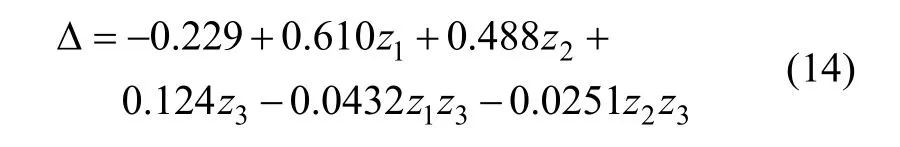
即

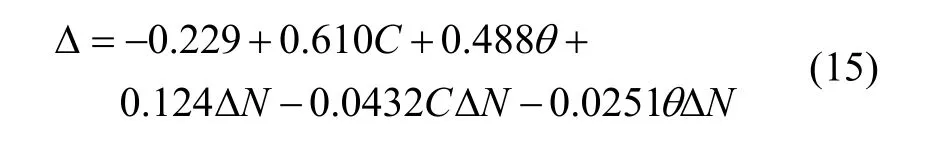
结合回归方程，综合考虑，取C=0.51，θ=0.57，ΔN=6，即(-1, -1, 1)水平。回归结果为Δ=0.89 mm，Matlab计算结果为Δ=0.87 mm，dBz=0.1079 T/m，符合控制指标。

4 结 论

随着冷原子技术的逐渐成熟，困扰冷原子陀螺仪实际应用的稳定性、体积和功耗问题正在逐步得到解决。在欧美大型国家计划的支持下，冷原子陀螺仪正逐渐走向工程化。欧美国家计划于2013～2014年完成冷原子惯性导航系统装机试飞工作，并最早于 2018年正式投入使用[13-14]。这些进展意味着冷原子陀螺仪的工程化、实用化已经迫在眉睫。

本文从环形电流的磁场分布模型出发，建立了三维磁光阱磁场线圈的数学模型；通过计算机仿真，对三维磁场系统的主要制造和装调误差——同轴度误差、平行度误差、线圈不对称和内径不对称——对磁场零点和梯度的影响进行了分析和比较，并利用最优近似饱和设计进行二次数学回归，通过优选得到了关键制造和装调参数的容差限。该工作为小型化冷原子陀螺仪三维磁场系统的工程化设计和制造提供了理论依据和参考价值。

（

）：

[1] Clauser J F. Ultra-high sensitivity accelerometers and gyroscopes using neutral atom matter-wave interferometry [J]. Physica B, 1988, 151: 262-272.

[2] Committee on Universal Radio Frequency System for Special Operations Forces, Standing Committee on Research, Development, Acquisition Options for U.S. Special Operations Command, National Research Council. Toward a universal radio frequency system for special operations forces[M]. Washington: National Academies Press, 2009.

[3] Schmidt G T. INS/GPS technology trends[R]. Massachusetts Institute of Technology, 2010.

[4] United States Air Force Chief Scientist (AF/ST). Report on technology horizons: a vision for air force science & technology during 2010-2030[R]. United States Air Force, 2010.

[5] 张学峰，许江宁，周红进. 原子激光陀螺[J]. 中国惯性技术学报，2006，241(5)：86-88.

ZHANG Xue-feng, XU Jiang-ning, ZHOU Hong-jin. Atom laser gyroscope[J]. Journal of Chinese Inertial Technology, 2006, 241(5): 86-88.

[6] 谢征，刘建业，赖际舟. 基于低温物理效应的新型超高精度陀螺仪研究综述[J]. 中国惯性技术学报，2007，15(5)：606-611.

XIE Zheng, LIU Jian-ye, LAI Ji-zhou. Research status of new high-precision gyroscope based on cryogenic physical effects[J]. Journal of Chinese Inertial Technology, 2007, 15(5): 606-611.

[7] 秦永元，游金川，赵长山. 利用原子干涉仪实现高精度惯性测量[J]. 中国惯性技术学报，2008，16(2)：244-248.

QIN Yong-yuan, YOU Jin-chuan, ZHAO Chang-shan. High accuracy inertial measurement based on atom interferometer[J]. Journal of Chinese Inertial Technology, 2008, 16(2): 244-248.

[8] Fang J C, Qin J. Advances in atomic gyroscopes: a view from inertial navigation applications[J]. sensors, 2012, 12(5): 6331-6346.

[9] Kitching J, Knappe S, Donley E A. Atomic sensors – a review[J]. IEEE Sensors Journal, 2011, 11(9): 1749-1758.

[10] 李攀，李俊，刘元正，等. 基于冷原子技术的导航传感器现状与发展[J]. 激光与光电子学进展，2013(11)：35-43.

LI Pan, LI Jun, LIU Yuan-zheng, et al. Current status and development of navigation sensors based on cold atoms [J]. Laser & Optoelectronics Progress, 2013(11): 35-43.

[11] Takase K. Precision rotation rate measurements with a mobile atom interferometer [D]. USA: Stanford, 2008.

[12] AOSense. Accelerometer for space applications based on light-pulse atom interferometry[EB/OL]. (2011-09-08) [2013-02-02]. https://ehb8.gsfc.nasa.gov/sbir/docs /public/ recent_elections/SBIR_11_P1/SBIR_11_P1_115522/brief chart.pdf.

[13] DARPA. Precision inertial navigation systems(PINS) [EB/OL]. (2010-12-30)[2013-02-02]. http://www. darpa.mil/ Our_Work/DSO/Programs/Precision_Inertial_Navigation _Systems_(PINS).aspx.

[14] Suriano M A. Robust technology to augment or replace the US reliance on the global positioning system[R]. Air University, 2011.

Tolerance design for three-dimension magnetic field system of cold atom gyroscope

LI Pan, LIU Yuan-zheng, WANG Ji-liang
(Flight Automatic Control Research Institute, Xi’an 710065, China)

Magnetic system of magneto-optical trap is an important part of high-precision cold atom gyroscopes. With the continuous decreases of gyroscope volume and improvements of integration, the effects of manufacturing and assembly errors of magnetic system on gyroscope performance are increasing. These errors will cause the field’s bias drift and gradient change, reduce work efficiency and quality of cold atom clouds, and ultimately affect the gyroscope performance. Based on the analysis of field distribution of three-dimension magnetic-optical trap and combined with the mathematical modeling and computer simulation, the effects of main manufacturing and assembly errors on the magnetic fields are analyzed and compared. In view of the present thresholds, the reasonable tolerance limits of key manufacturing and assembly parameters are designed by experimental design and regression analysis. And the theoretical basis for the design and manufacture of three-dimension magnetic system of miniaturized cold atom gyroscope is also provided.

cold atom gyroscope; magneto-optical trap; magnetic field system; tolerance design

1005-6734(2014)05-0671-06

10.13695/j.cnki.12-1222/o3.2014.05.022

U666.1

A

2014-05-13；

2014-09-26

总装十二五航空支撑资助项目（61901060301）

李攀（1983—），男，工程师，从事量子传感器技术研究。E-mail：lp_forever5281@sina.com