船体变形测量中激光陀螺误差的抑制机理

吴 伟，秦石乔，杨云涛，王省书

（国防科学技术大学 光电科学与工程学院，长沙 410073）

船体变形测量中激光陀螺误差的抑制机理

吴 伟，秦石乔，杨云涛，王省书

（国防科学技术大学 光电科学与工程学院，长沙 410073）

针对激光陀螺测量误差对船体自主变形测量精度的影响问题，在角速度匹配方程基础上提出了一种信号同步积分求解变形角的方法。根据船体角运动的周期特性，利用实测船体运动角速度信号产生时序同步信号，并与角速度匹配方程相乘得到新的测量方程，使得包含变形角信息的有用信号通过积分得到增强，而陀螺误差则被调制为随机信号，积分后被抑制，从而提高了测量方程的信噪比。仿真结果表明：当积分时间大于5 min时，变形角测量误差的均方根值（RMS）小于10"，且随着积分时间的增加，测量精度将会提高。这种同步积分方法不需要对陀螺误差建模即可实现对船体变形的高精度测量，而且直观地解释了在激光陀螺误差存在条件下自主变形测量误差不随时间发散的原因。

船体变形；激光陀螺；零偏误差；随机误差；同步积分法

舰船在海浪冲击、载荷变化和日照等因素影响下将产生船体变形[1]。船体变形将使得雷达、光电跟瞄、火炮等武器系统坐标系与中心主惯导参考坐标系之间产生坐标系失调，从而严重影响坞内基准标校效果，导致武器作战基准的精度下降，甚至失效[2-3]。为了消除船体变形对导航坐标基准的影响，目前有局部基准法[3]和激光陀螺自主变形测量[4-5]等方法。局部基准受陀螺和加速度计测量误差的限制，其精度随时间发散，如果提高局部基准的精度，成本也会大大增加。自主变形测量方法[4-5]利用激光陀螺对角度敏感、瞬时角分辨率高的优点，用两套激光陀螺组合体（LGUs）同时测量船体运动角速度，通过比较两套系统输出的角速度测量值的差异，实现船体任意两点变形的高精度测量。该方法具有体积小、自主测量等优点，越来越受到国内外研究者的重视[5-10]。

影响自主变形测量方法精度的因素主要有船体变形模型误差和测量器件误差等，船体变形模型的影响问题已得到初步解决[6,11]，但是测量器件误差的影响问题还有待深入研究。自主变形测量用激光陀螺作为传感器，其误差源包括零偏常值误差、零偏稳定性、随机游走、量化噪声等。在研究中，常通过对陀螺误差建模的方法实现测量噪声与信号的分离[4-12]。文献[4]中用高斯白噪声模型对陀螺随机误差进行建模；文献[5]根据激光陀螺的特性，将陀螺测量误差分为零偏常值误差和随机误差，其中随机误差用一阶马尔科夫模型来描述；文献[12]研究发现，陀螺零偏常值误差对变形测量精度没有影响，但是随机游走误差将导致测量结果在一定误差范围内波动。在应用中，陀螺误差建模法需要预先设置较准确的模型参数，利用观测方程，通过 Kalman滤波实现对陀螺测量误差的最优估计。但是，准确的陀螺模型参数往往无法获得，即使通过标定得到，但是长时间工作之后也会发生变化。

针对激光陀螺误差对自主变形测量精度的影响问题，本文根据船体周期角运动特性，提出一种基于信号同步积分解析求解变形角的方法。这种方法不需要对陀螺误差建模就可以实现对船体变形角的最优估计，而且可以直观地解释自主变形测量中陀螺误差的抑制机理。

1 自主变形测量原理

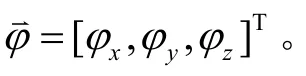
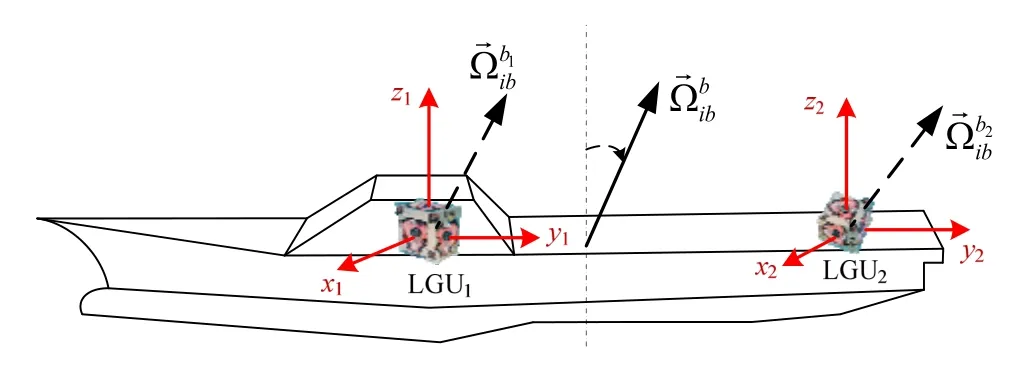
图1 船体自主变形测量原理示意图Fig.1 Measurement schematic of ship deformation

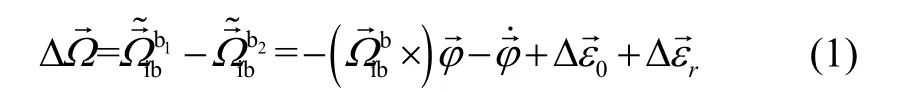
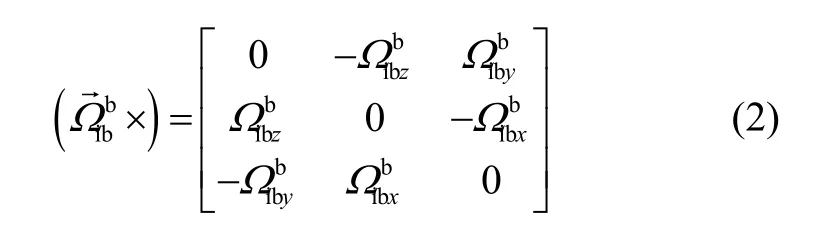
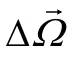
陀螺零偏常值误差模型为：

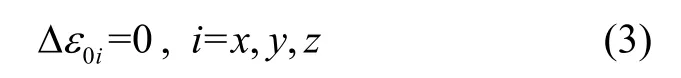
随机误差常用白噪声驱动的一阶微分方程来描述[6]：

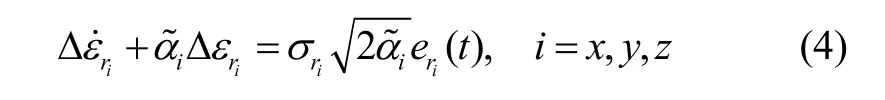
2 陀螺零偏误差抑制原理

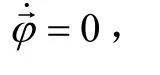
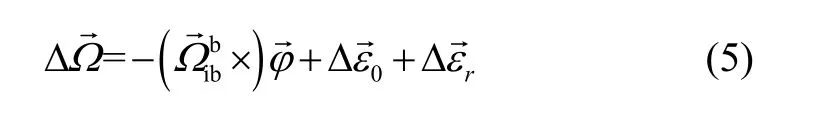
将式(2)代入式(5)，展开得：

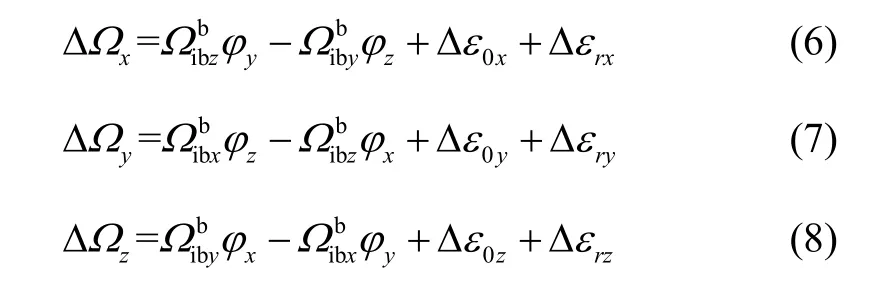
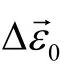
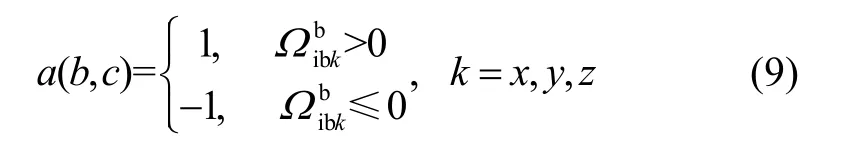
根据式(7)和(8)所示的坐标投影关系，x方向的变形角φx将在y和z方向角速度差值ΔΩy和ΔΩz上产生投影。如果用时序同步信号a与ΔΩy和ΔΩz作点乘，使得原来均值为零的随机信号ΔΩy和ΔΩz变为大于或小于0的倍频信号，正负号由时序同步信号与角速度的初始相位关系决定。经过时序同步后的角速度差值信号再经过累加积分，周期信号得到增强，而陀螺零偏与随机漂移误差与同步信号相乘后的相位是无序的，因此通过累加积分就可以抑制陀螺误差。

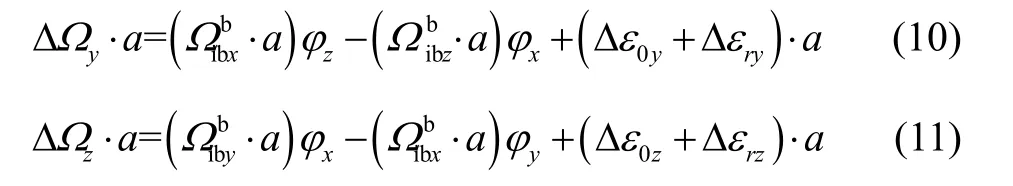
其中，“·”表示信号点乘。

同理，用时序同步信号b乘以方程(6)和(8)，用时序同步信号c乘以方程(6)和(7)，可得：

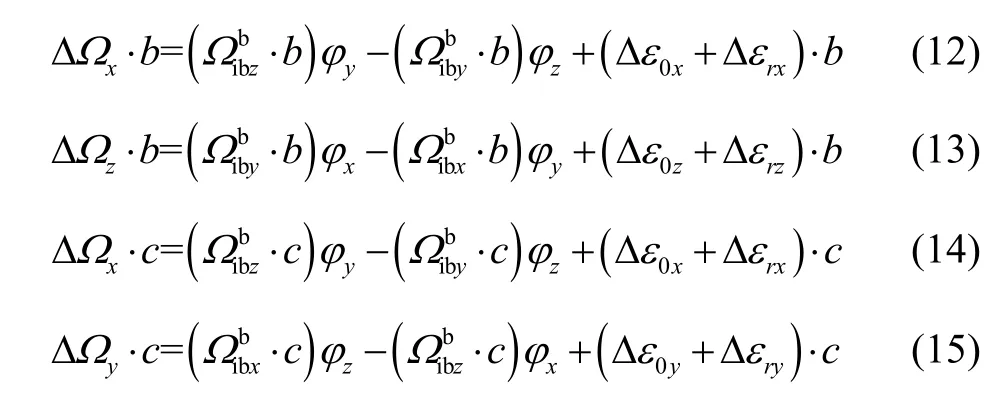
对式(10)在(0, t)时间内积分，可得：

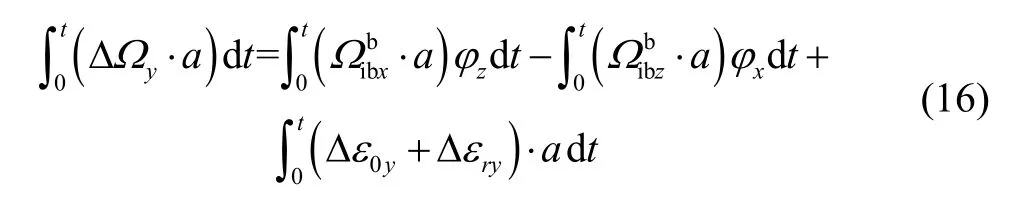
上式右边最后一项为陀螺误差与时序同步信号相乘后的积分，下面对此项的积分结果作详细分析。

如图2所示，如果角速度信号为正弦波，产生的时序同步信号的正负半周期对称，经过一个周期积分的结果为 0，长时间积分值不随时间增长；如果角速度波形为非正弦波，一个周期的时序信号积分结果等于正负周期所围面积的差值，为小量，且随积分时间的增加，时序信号积分值不随时间增长。船体在波浪作用下的角运动为平稳随机过程，所以时序同步信号a、b、c的时间积分也为一个小量。对于式(16)中的陀螺常值误差 Δε0y，其同步积分结果为：

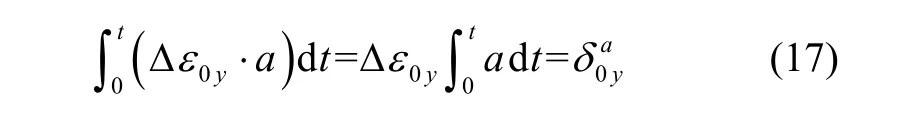
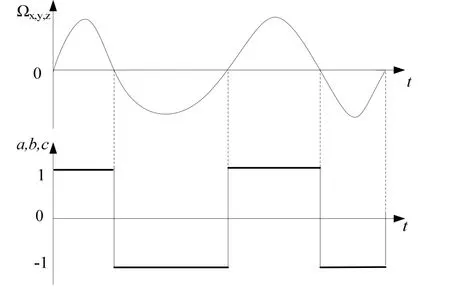
图2 角速度信号转化为时序同步信号原理示意图Fig.2 Schematic diagram of converting ship’s angular rate signal into time synchronization signal

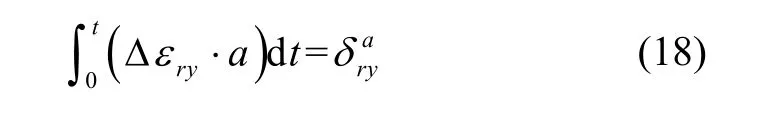
式中， Δεry中的具有白噪声特性的角速度随机噪声的同步积分结果为0，而零偏漂移项的周期远大于时序同步信号a的周期，在一个积分周期内近似为常值。因此， Δεry的同步积分结果也不随时间增长。

将式(17)和(18)代入式(16)，可得：

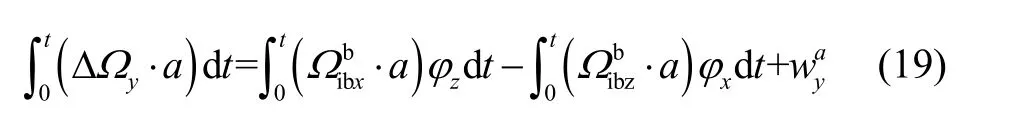
同理，对式(11)～(15)进行积分，并用最小二乘方法求解，观测方程为：

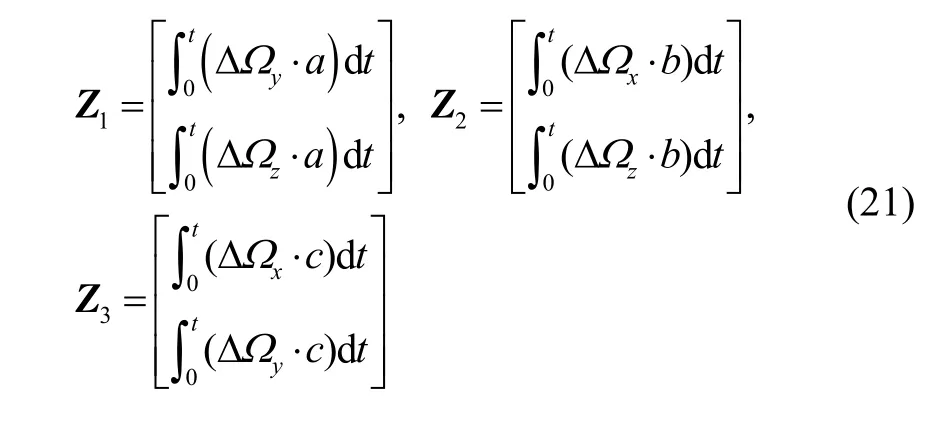
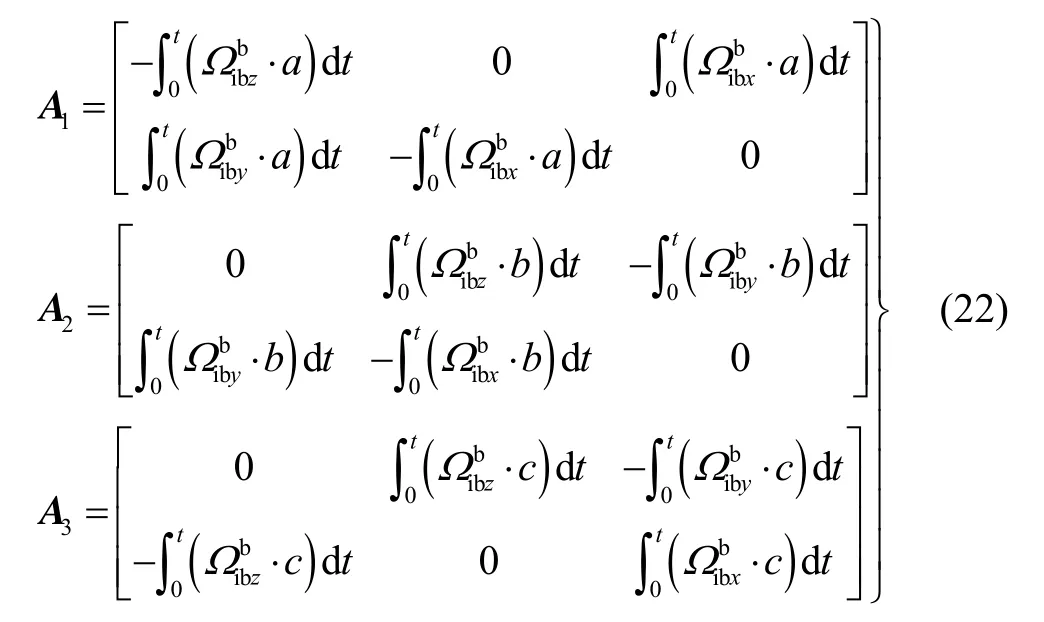
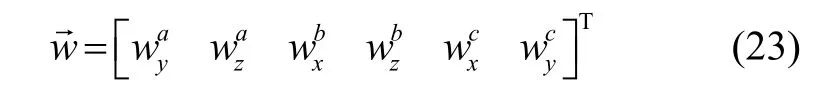
将式(21)～(23)代入式(20)，利用最小二乘法求解可得变形角：

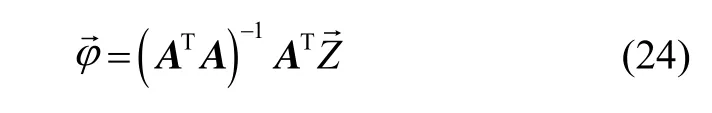
根据式(20)～(24)，由两组LGUs测量的角速度，通过同步积分即可求得船体变形角。

从以上理论分析可以看出，自主变形测量方程中陀螺零偏和随机漂移误差受船体周期运动调制，通过同步积分而被抑制，测量误差不随时间发散，反而是积分时间越长，求解精度越高。同时可看出，也只有在海上周期摇摆条件下，陀螺测量误差才能与变形角有效分离。因此，自主变形测量是利用了船体周期运动抑制陀螺误差的影响，变形测量误差不随时间增长而发散。

3 仿真实验验证

3.1 仿真条件设置

下面用实测船体姿态数据构建仿真环境，以验证自主变形测量方法对陀螺测量误差的抑制效果。仿真条件设置如下：

① 船体姿态数据采用某船在三级海况条件下的实测数据，如图3所示；

③ 根据公式(5)，角速度匹配测量方程只与两套LGUs的陀螺零偏差值和随机误差的差值有关。

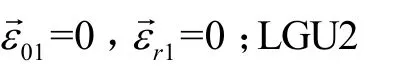
根据以上仿真条件，产生LGU1和LGU2的陀螺输出数据，采样频率为 20 Hz，并用同步积分方法求解船体变形角。

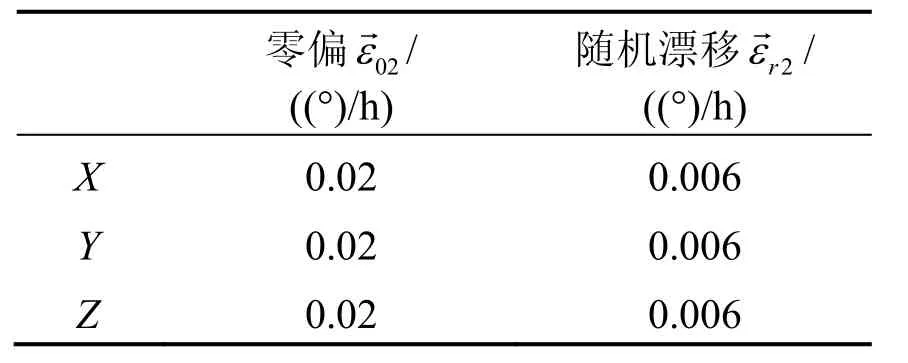
表1 LGU2的陀螺测量误差的模型参数Tab.1 Gyro error parameters of LGU2

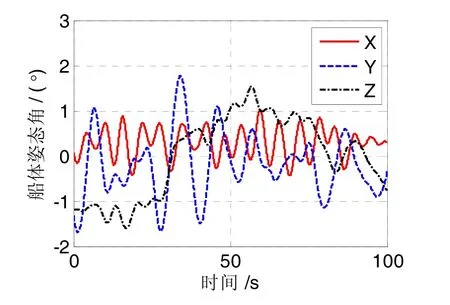
图3 实测船体姿态变化曲线Fig.3 Curves of real-measured ship attitude

3.2 结果与分析

下面以x方向时序同步信号与y方向的测量信号同步结果为例来说明陀螺误差的抑制机理。根据公式(9)，由船体运动角速度信号产生时序同步信号。图4所示x方向的船体运动角速度及时序同步信号a，可以看出，船体运动角速度信号为类正弦运动，其时序同步信号为方波信号。图5所示为LGU2的y方向陀螺的零偏误差和随机误差的原始信号直接积分结果与经过时序信号同步之后的积分结果比较，积分时间长度为3 h。由图5(a)可见，陀螺零偏误差随积分时间线性增长，3 h的累积误差为216"，而经过时序同步之后的陀螺零偏误差的积分值不随时间增大，最大误差只有1"；由图5(b)可见，陀螺随机误差的积分结果随时间发散，3 h积分结果的均方差为19.3"，而同步积分后的随机误差积分结果的均方差为7.3"，可见同步积分后的随机误差受到抑制。用x方向的时序同步信号与ΔΩy相乘，得到同步后的信号如图6所示。图6中，同步前100 s数据的均值为-1.01×10-6rad/s，同步后ΔΩy的均值变为1.41×10-5rad/s，均值提高了14倍。对经过时序同步后的角速度差值信号进行积分，数值就会变大，而陀螺噪声误差积分结果反而变小，从而达到增强信号、抑制噪声的目的。

利用上面提出的同步积分方法求解船体变形角，得到变形角测量误差随积分时间的变化曲线，如图 7所示。由图7可见，当积分时间大于5 min时，变形角测量误差的均方根值（RMS）即优于 10"，而且随着积分时间的增加，变形角的测量精度将提高。

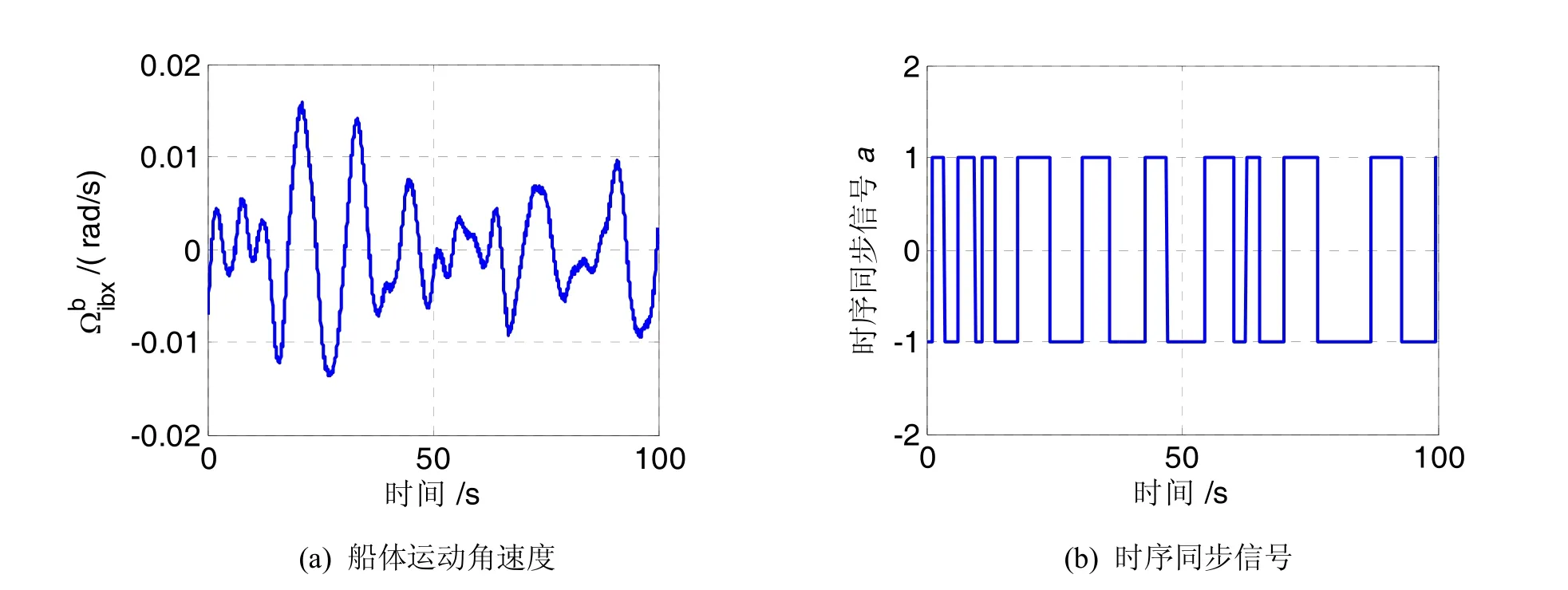
图4 船体运动角速度信号及其同步时序信号Fig.4 Ship’s angular rate signal and its time synchronization signal

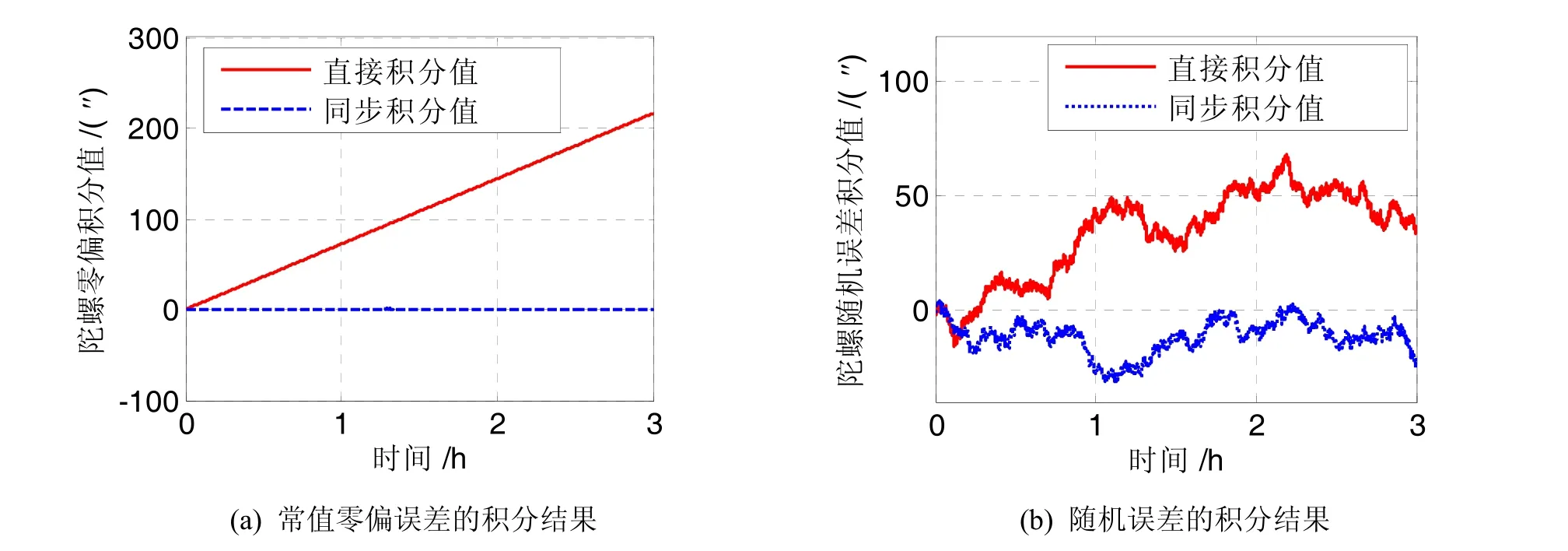
图5 LGU2 y方向陀螺零偏和随机误差的直接积分与同步积分结果比较Fig.5 Comparison of directly integral results and synchronization integral results for bias and random errors of LGU2 y-gyro

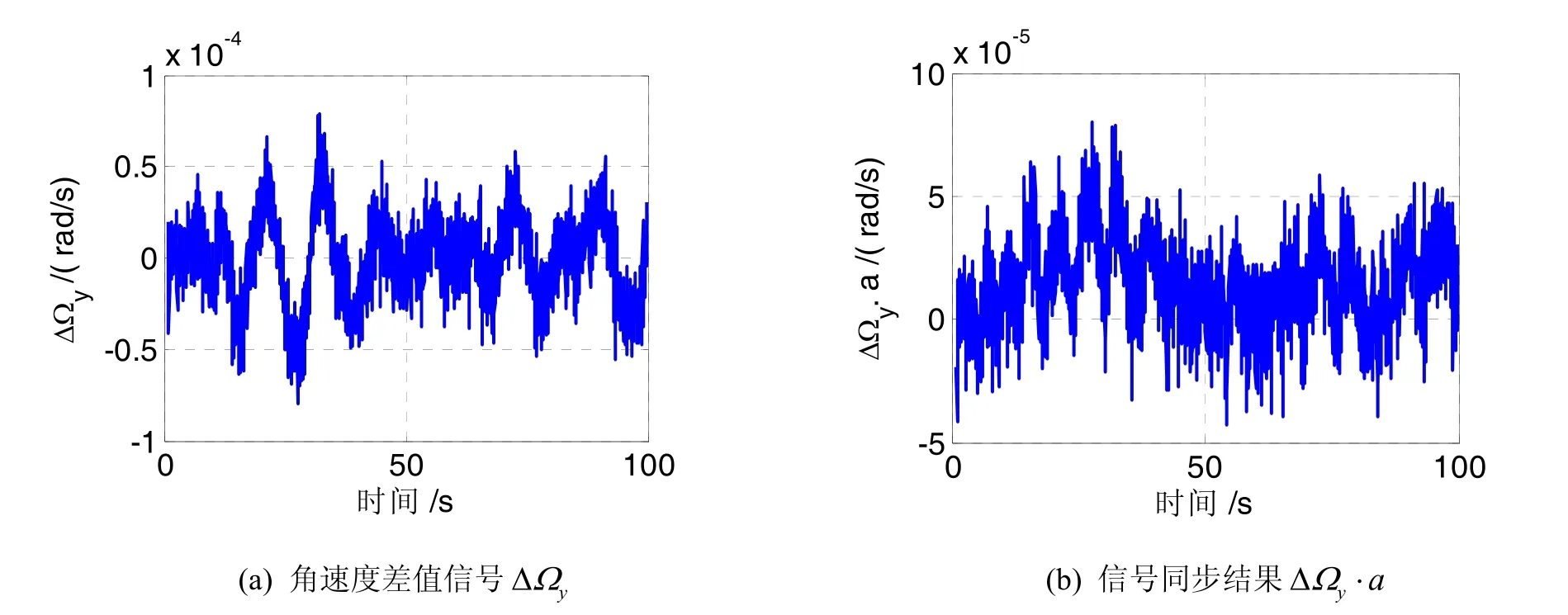
图6 角速度差值信号的同步结果Fig.6 Difference signal of ship’s angular rate and its synchronization results

从上面仿真结果可以看出，由于船体角运动特有的周期性，可以采用同步积分方法使得包含变形角信息的有用信号得到增强，而陀螺误差则被抑制，从而提高测量方程的信噪比，使得变形角的测量精度几乎不受陀螺常值零偏误差和随机漂移误差的影响。然而，同步积分方法只能适用于舰船在海上运动条件下的变形测量，对于其它运动平台，如果运动角速度不具有周期性，陀螺误差与变形角信号将不能被分离，导致变形角测量误差受陀螺随机误差的影响而逐渐发散。因此，同步积分方法只适用于海上周期摇摆运动条件下的船体变形测量。

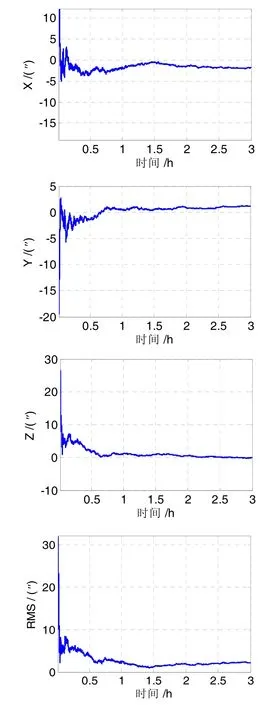
图7 变形角测量误差随积分时间的变化曲线Fig.7 Ship deformation measurement errors vs. measurement time

4 结 论

本文提出了一种基于信号同步积分求解变形角的方法，可以有效抑制自主变形测量中激光陀螺零偏和随机误差的影响。同步积分方法利用了船体角运动的周期特性和测量方程各方向之间的投影关系，使得包含变形角信息的有用信号通过同步积分得到增强，而陀螺误差同步积分后被调制为随机信号，通过积分则误差被抑制，从而提高了测量精度。仿真结果表明：当积分时间大于5 min，变形角测量误差的均方根值（RMS）小于10"，而且随着时间的增加，测量精度将会提高。此外，本文的理论分析和仿真结果表明，自主变形测量精度不随时间发散的根本原因是陀螺零偏和随机误差受船体运动的周期调制而被抑制。因此，自主变形测量技术可以实现船体变形角的高精度、长时间测量，利用该方法可以很方便地建立全船的统一空间基准，实现全船的信息共享，从而提高舰载武器的作战效能。

（

）：

[1] 郑梓祯，刘德耀，蔡迎波. 船用惯性系统试验安装标校与变形测量[J]. 中国惯性技术学报，2004，12(4)：1-6.

ZHENG Zi-zhen, LIU De-yao, CAI Ying-bo. Installation adjustment and deformation survey for marine inertial system test[J]. Journal of Chinese Inertial Technology, 2004, 12(4): 1-6.

[2] Titterton D H, Weston J L. The alignment of ship launched missile IN systems[C]//Controller HMSO. London, 1989.

[3] Day D L, Arrud J. Measuring structural flexure to improve precision tracking[R]. WA, AD A364862, June, 1999.

[4] 万德钧，刘玉峰. 消减舰船变形的影响和为全舰提供高精度姿态基准[J]. 中国惯性技术学报，2005，13(4)：77-82.

WAN De-jun, LIU Yu-feng. Summary on removing influence of ship deformation and providing accuracy attitude reference for warship[J]. Journal of Chinese Inertial Technology, 2005, 13(4): 77-82.

[5] Schnider A M. Kalman filter formulations for transfer alignment of strap down inertial units[J]. Navigation, 1983, 30(1): 72-89.

[6] Mochalov A V, Kazantasev A V. Use of the ring laser units for measurement of the moving object deformation[C]//Proceedings of SPIE 4680. 2002: 85-92.

[7] Majeed S, Fang J. Comparison of INS based angular rate matching methods for measuring dynamic deformation[C] //Proceedings of the 9th International Conference on Electronic Measurement & Instruments. Beijing, China, 2009: 332-336.

[8] Sun F, Guo C J, Gao W, et al. A new inertial measurement method of ship dynamic deformation[C]//Proceedings of International Conference Mechatronics and Automation. Harbin, China, 2007: 3407-3412.

[9] 郑佳兴，秦石乔，王省书，等. 基于姿态匹配的船体形变测量方法[J]. 中国惯性技术学报，2010，18(2)：175-180.

ZHENG Jia-xing, QIN Shi-qiao, WANG Xing-shu, et al. Attitude matching method for ship deformation measurement[J]. Journal of Chinese Inertial Technology, 2010, 18(2): 175-180.

[10] Wu W, Qin S, Chen S. Coupling influence of ship dynamic flexure on high accuracy transfer alignment[J]. International. Journal of Modelling, Identification, and Control, 2013, 19(3): 224-234.

[11] Wu W, Chen S, Qin S. Online estimation of ship dynamic flexure model parameters for transfer alignment[J]. IEEE Transaction on Control Systems Technology, 2013, 21(5): 1666-1678.

[12] Zheng J, Qin S, Wang X, et al. Influences of gyro biases on ship angular flexure measurement[C]//Proceedings of 2011 Symposium on Photonics and Optoelectronics. Wuhan, China, May 16-18, 2011: 1-4.

[13] Bishop R, Price W G. Hydroelasticity of ships[M]. London: Cambridge University Press, 1979.

[14] Wu J S, Sheu J J. An exact solution for a simplified model of the heave and pitch motions of a ship hull due to a moving load and a comparison with some experimental results[J]. Journal of Sound and Vibration, 1996, 192(2): 495-520.

Error suppression mechanism for ring laser gyro in ship deformation measurement

WU Wei, QIN Shi-qiao, YANG Yun-tao, WANG Xing-shu
(School of Opto-Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

A synchronization integral method based on the angular matching function is presented for reducing the influence of the ring laser gyro (RLG) error in ship deformation measurement. Specifically, the method produce the synchronization time series from the ship angular rate signal according to the period characteristics of ship angular motion, and then the time series are multiplied by the angular matching function to get a new measurement function. As a result, the signals with the deformation information are strengthen through integral, while the RLG errors are modulated to random signals and reduced through integral. Therefore, the signal to noise ratio of measurement function is improved through synchronization integral. Simulation results show that the deformation measurement can achieve an accuracy of 10 arcsecs (RMS) within 5 min, and the accuracy can even be improved when with longer integral time. This synchronization method can solve the ship deformation values to reach high accuracy without requiring a priori knowledge of RLG error model. Additionally, it also directly depicts the reason why ship deformation measurement error is not increased with time when RLG errors exist.

ship deformation; ring lager gyro; bias error; random error; synchronization integral method

吴伟（1985—），男，讲师，研究方向为光电测控技术。E-mail：weiwunudt@gmail.com

1005-6734(2014)05-0665-06

10.13695/j.cnki.12-1222/o3.2014.05.021

U666.1

A

2014-05-22；

2014-08-29

国家自然科学基金资助项目（11172323，61275002）