基于扩展卡尔曼滤波的X射线脉冲星相对导航方法

夏红伟，刁雁华，马广程，曹 卓，王常虹

（1. 哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001；2. 上海航天控制技术研究所，上海 200233）

基于扩展卡尔曼滤波的X射线脉冲星相对导航方法

夏红伟1，刁雁华1，马广程1，曹 卓2，王常虹1

（1. 哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001；2. 上海航天控制技术研究所，上海 200233）

X射线脉冲星作为一种天然时间基准，具有良好的周期稳定性，在深空探测航天器自主导航方面具有重要的应用前景。针对绝对导航的整周模糊度求解问题和相对导航的预报相位、标称轨道存储问题，提出了一种改进的相对导航方法，将前一时刻的航天器位置作为相对导航基准，建立航天器轨道动力学模型，采用扩展卡尔曼滤波算法，确定航天器的位置。最后，进行了数学仿真研究，仿真结果表明：脉冲星相对导航改进方案的导航精度达到1 km，滤波器一致渐进稳定，能够快速抑制初始误差和轨道根数的干扰，验证了导航方案的正确性和可行性。

深空探测；相对导航；X射线脉冲星；扩展卡尔曼滤波

X射线脉冲星具有良好的周期稳定性，作为一种天然时间基准，在深空探测航天器自主导航方面具有重要的应用前景[1]。目前国内的研究成果主要采用脉冲星绝对导航方式[2]，围绕整周模糊度的求解问题，提出了最小二乘法、空间搜索法和卡尔曼滤波方法[3-5]。前两种方法的导航精度不高，且受轨道根数等因素的影响较大。卡尔曼滤波方法将系统模型线性化，影响了导航精度。此外，针对深空探测自主导航问题，航天器无法借助外界信息，因此绝对导航中的预报相位和标称轨道等相关数据需要预先存储在计算机内部，占用了大量的存储单元，在工程实践中难以实现。

鉴于绝对导航在工程实践中存在的问题，相对导航定位方法成为是脉冲星导航的主要发展趋势，通过改变导航基准，在不影响导航精度的前提下，简化了轨道动力学模型。Emadzadeh提出了脉冲星相对导航的基本原理[6]，Ray进一步分析确认了脉冲星相对导航的可行性[7]。Kim和Munoz基于扩展卡尔曼滤波，进行了脉冲星相对导航仿真，得到了较为理想的导航精度[8-9]。但是上述导航方法均选取地球质心作为导航基准，只适用于地球轨道航天器，而且使用量测相位与预报相位之差作为滤波算法的量测值，仍然没有解决相关数据的存储问题。

针对上述问题，本文提出了一种改进的脉冲星相对导航方法，选取前一时刻航天器的位置作为导航基准，采用扩展卡尔曼滤波确定航天器位置，避免了绝对导航方式中对整周模糊度的讨论，解决了目前相对导航方案中的预报相位存储问题。数学仿真分析结果表明，滤波估计结果与真实轨道具有高度的一致性，验证了本文提出的导航方法的正确性和可行性。

1 相对导航

相对导航是以量测航天器与导航参考基准之间的相对距离、方位信息为基础，进而确定出相对位置和姿态信息[10]。在脉冲星的绝对导航中，需要预先在星载计算机上注入预报相位数据，这会占用大量的存储空间，增加导航系统的负担。

脉冲星的相对导航方式选取航天器、地球质心、拉格朗日点或者太阳系行星等作为导航参考基准，确定航天器相对参考基准的位置信息。相对于绝对导航，脉冲星的相对导航方式在量测信息处理以及导航解算中的复杂度均有一定程度的降低。

鉴于脉冲星相对导航相比于绝对导航的优越性，本文提出了一种相对导航改进方法：①选取航天器前一时刻t- T的位置作为当前t时刻的相对导航参考基准；②根据脉冲星时间相位模型建立参考基准的相位传播模型；③航天器上的星载原子时钟输出当前时刻的量测相位；④采用相关导航定位方法，解算得到航天器相对于非惯性系的位置。

以观测单颗脉冲星为例，选取t- T时刻航天器的位置作为t时刻的相对导航参考基准，利用t- T时刻的量测相位 φ( t -T)结合脉冲星时间相位模型得到t时刻脉冲信号到达相对参考基准的预报相位φ( t|t -T)的传播方程为：

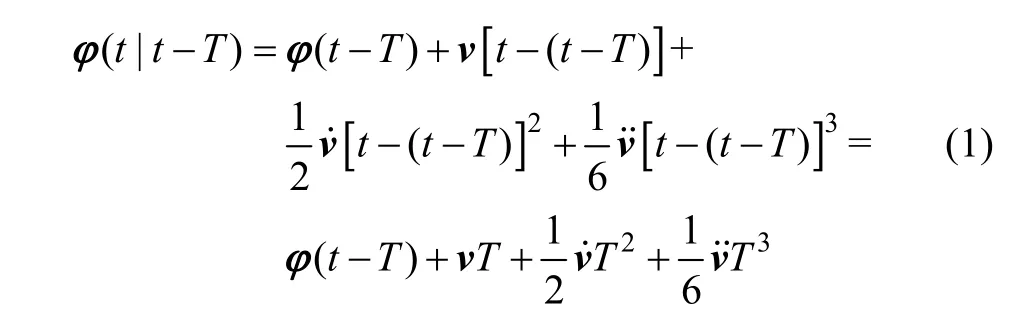
式中，φ( t -T)是t- T时刻的量测相位，φ( t|t -T)是根据 φ( t -T)得到的t时刻预报相位，v、v˙和v˙分别是脉冲信号频率及其一阶、二阶导数，T是星载原子钟的采样时间。根据式(1)，已知采样时间T，便可以在线递推解算得到预报相位 φ( t|t -T)，不需要预先在星载计算机上存储数据，节约了资源，且容易实现。

星载原子时钟检测到当前t时刻脉冲信号的到达相位 φ( t)，结合预报相位 φ( t|t -T)，根据式(2)计算得到的航天器当前时刻与参考基准的相对位置r，同时对多颗脉冲星进行天文观测，就可以确定航天器的相对位置，其原理图可用图1表示。

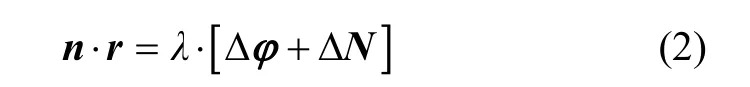
以地球同步卫星为例，脉冲星的空间方位信息、信号周期、频率及其各阶导数均可经过长期的天文观测得到，星载原子时钟的采样时间取10s，则相对距离约为31 000 m。 φ( t|t -T)与 φ( t -T)的相位差约为100，与 φ( t)的相位差约为10-4，均大于星载原子时钟10-12的分辨率，可以被导航系统所辨识。因此本文提出的这种改进的脉冲星相对导航方法通过选取合适的相对导航参考基准，不再需要将时间信息统一在太阳系质心坐标系SSB，相对论效应引起的各种延迟可以互相抵消，解决了深空航天器预报相位的存储问题，适合在工程实践中使用。

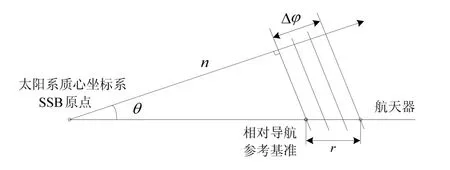
图1 航天器的相对导航定位方式Fig.1 Spacecraft relative navigation

2 导航位置的滤波与解算

2.1 航天器动力学模型的建立

相对导航选取t- T时刻航天器的位置信息作为t时刻的导航基准，相对距离r和速度v作为状态变量，建立轨道动力学模型：

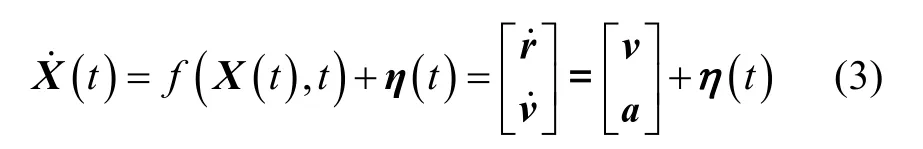
式中， η( t)是系统的高斯白噪声；a是航天器的加速度，其中包括二体加速度、中心天体的非球项引力势加速度、大气阻力加速度、第三天体产生的引力加速度、加速度的高阶小量等。对于地球轨道航天器，可以只考虑二体加速度，则 f( X (t),t)可以写成：

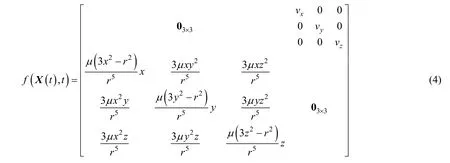
对该非线性系统线性化和离散化处理，得到偏差状态方程的离散形式：

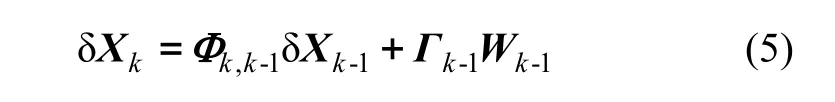
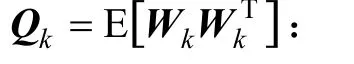
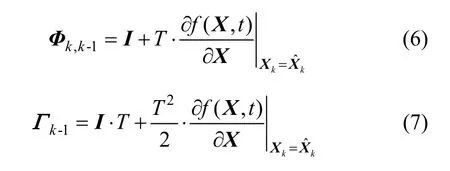
2.2 量测方程

同时观测n颗脉冲星，星载原子时钟检测到各个脉冲信号的到达相位为 φk，根据式(1)， k-1时刻的脉冲相位最优估计为，结合脉冲星时间相位模型，计算得到k时刻脉冲信号到达相对导航参考基准的预报相位：

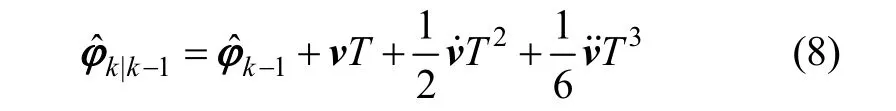
以量测相位 φk与预报相位之差 Δφk作为扩展卡尔曼滤波算法的量测值 Zk，构造量测方程。根据相对导航理论，保证整周模糊度降低为0，结合式(2)，可以得到量测方程：

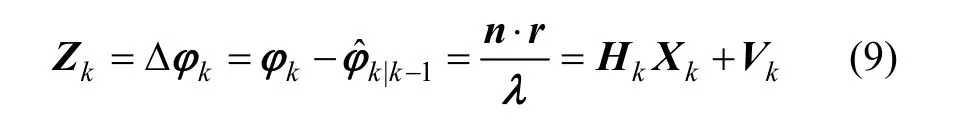
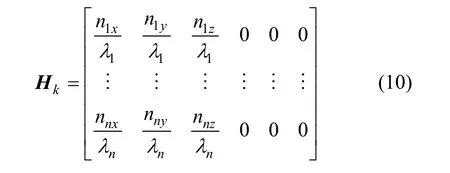
2.3 定位信息解算

扩展卡尔曼滤波（Extened Kalman Filter, EKF）是围绕最优状态估计的非线性滤波，分为“预测+更新”两个阶段。扩展卡尔曼滤波本质上是通过一阶泰勒近似，对非线性系统先后进行线性化和离散化处理的最小方差估计，递推方程如下：

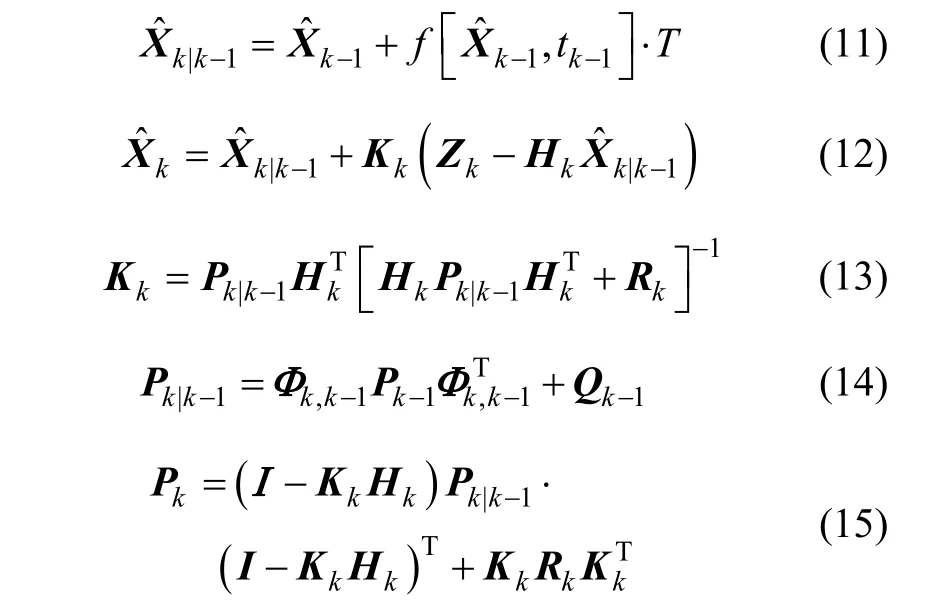
式中，P是状态误差方差矩阵，K是滤波增益矩阵。

根据2.1节的轨道动力学模型和2.2节的量测方程，结合EKF算法，解算得到航天器当前位置的最优估计以及脉冲相位的最优估计，进一步由式(1)计算得到下一时刻的预报相位：

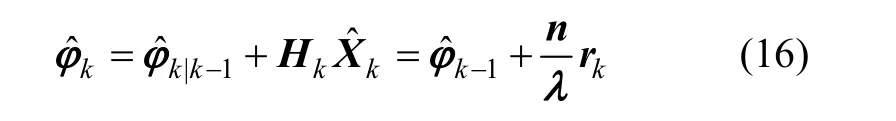
注：本文提出的上述基于EKF的脉冲星相对导航属于最优估计问题，不需要借助标称轨道作为参考基准，将相对导航与扩展卡尔曼滤波相结合，解决了目前脉冲星导航中存在的预报相位和标称轨道的存储问题，便于工程实现。

3 相对导航仿真与分析

3.1 仿真结果

为了证明本文提出的基于 EKF的脉冲星相对导航改进方案的正确性和可行性，对典型地球轨道航天器进行数学仿真。以近地轨道、中高轨道和地球同步轨道为例，轨道根数如表所示，天文参数如表2所示。

选取前一时刻航天器位置作为导航基准，由于航天器速度有限，相对距离必定小于一个脉冲波长，保证了整周模糊度 ΔN = 0。

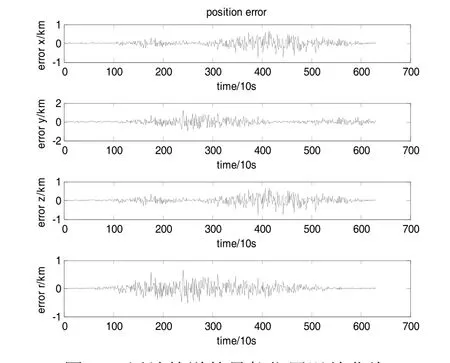
图2 a 近地轨道的导航位置误差曲线Fig.2 a Position error curves of the low orbit

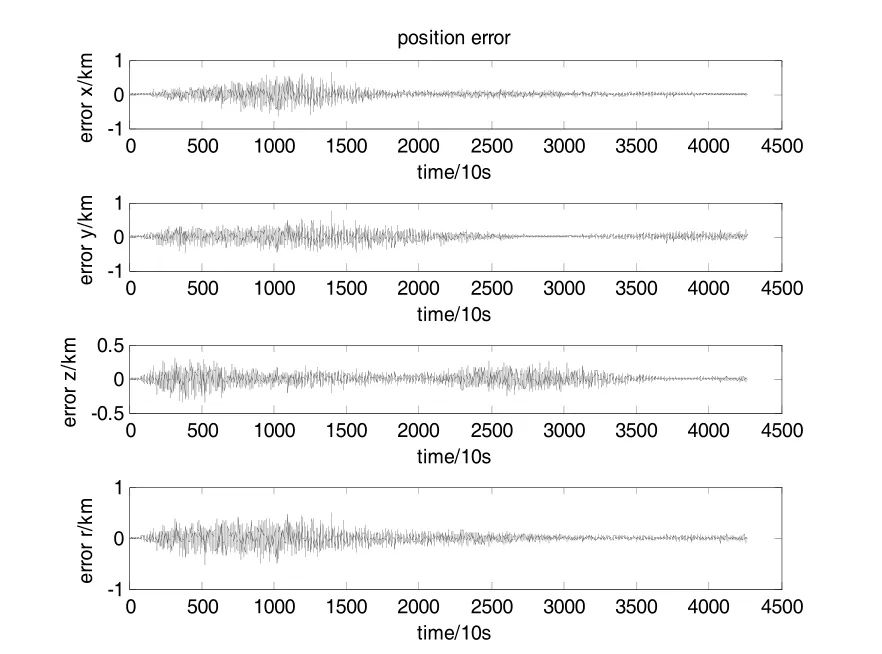
图2 b 中高轨道的导航位置误差曲线Fig.2 b Position error curves of the high orbit

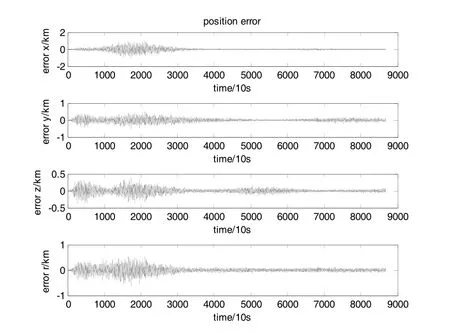
图2 c 地球同步轨道的导航位置误差曲线Fig.2 c Position error curves of the geosynchronous orbit

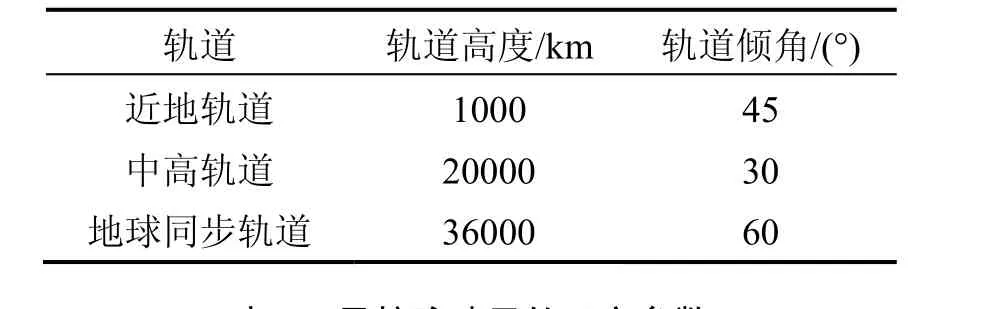
表1 典型地球轨道的轨道根数Tab.1 Orbital root numbers of the orbits

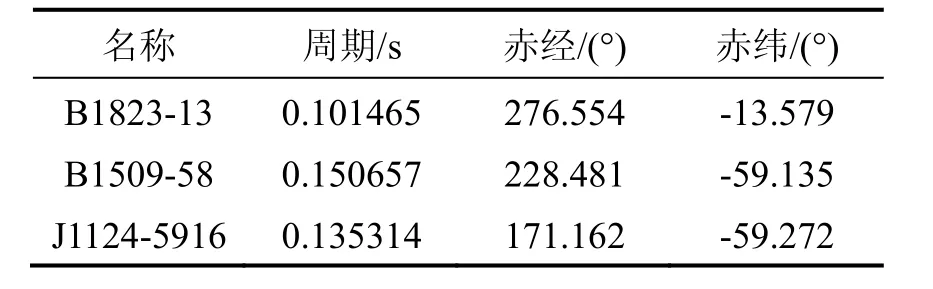
表2 导航脉冲星的天文参数Tab.2 Celestial parameters of the pulsars

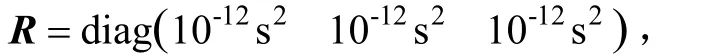
利用上述仿真数据，进行导航解算，得到航天器位置的最优估计与真值的误差曲线如表3和图2所示。

表3 地球轨道的导航精度Tab.3 Navigation accuracy of the orbits

3.2 滤波分析

① 可控性分析

根据古卓夫科夫可控性判据定理，如果过程噪声统计特性矩阵Q正定，若满足式(17)，则导航系统是完全随机可控的：

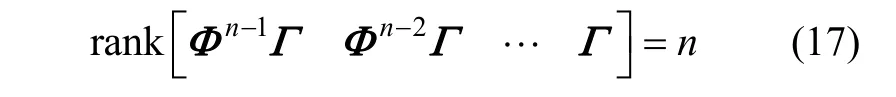
基于 EKF的脉冲星相对导航改进方案数学仿真中，系统的过程噪声满足高斯白噪声特性，Q阵是正定矩阵。将上述地球轨道的系统方程矩阵Φ和Γ代入，均满足等式(17)，说明所建立的导航系统是可控的。

② 可观测性分析

采用奇异值分析方法，构造系统的可观测性矩阵M，如式(18)所示：

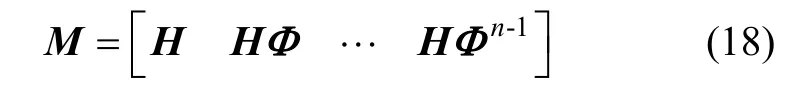
如果可观测性矩阵M的奇异值均不为0，则系统是完全随机可观测的。

构造上述地球轨道的可观测性矩阵M，计算相应的奇异值，如表4所示。可以看出，三条轨道的奇异值均大于0，并且奇异值越大，可观测性越好。

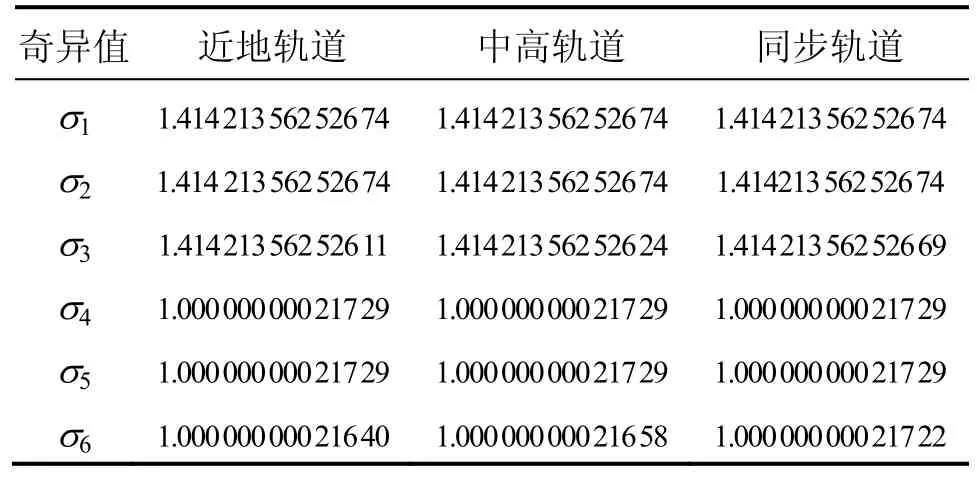
表4 可观测矩阵的奇异值Tab.4 Singular values of the observability matrix

③ 稳定性分析

根据滤波稳定性定理：如果系统是完全随机可控和完全随机可观测的，则EKF滤波器是一致渐进稳定的。

前面对导航系统的可控性和可观测性的讨论表明，本文提出的相对导航改进方案均满足完全随机可控和完全随机可观测的性质，所以随着时间的增长，滤波状态变量X及其误差方差阵P都不受所选初值的影响，滤波器一致渐进稳定。

3.3 导航精度分析

① 初始误差对导航精度的影响

以近地轨道为例，不改变其他参数，初始位置误差分别取1 km、2 km和5 km，所得航天器位置误差曲线如图3a所示。可见，EKF能够快速修正初始误差，也就是说初始误差对导航精度没有影响。

② 轨道高度对导航精度的影响

在不改变其他参数的条件下，考察三条典型轨道的导航精度，如图3b所示。可以看出，轨道高度对导航精度的影响不大，三个地球轨道航天器的导航精度均为1km。

③ 轨道倾角对导航精度的影响

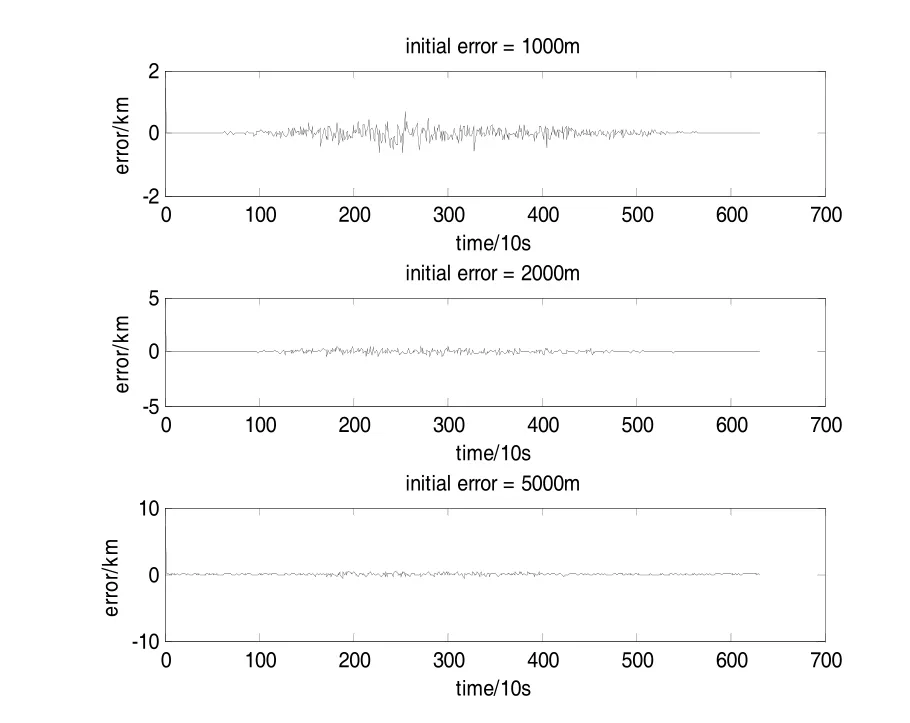
图3 a 1 km、2 km、5 km初始误差的位置误差曲线Fig.3 a Position error curves with initial position errors of 1 km, 2 km and 5 km

以近地轨道为例，分别考察30°、45°和60°的轨道倾角对导航精度的影响，如图3c所示。可以看出，轨道倾角对精度影响也不大，导航精度均为1 km，结合上述分析，说明基于EKF的脉冲星相对导航改进方案能够较好抑制轨道根数的干扰，获得较高的导航精度。

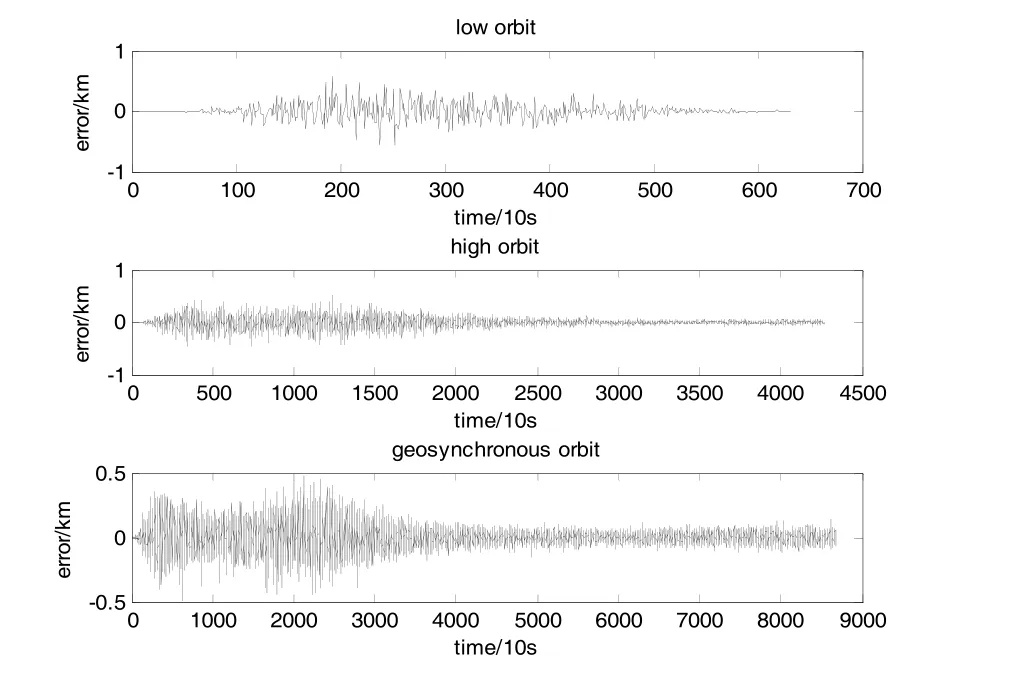
图3 b 不同轨道高度下的位置误差曲线Fig.3 b The position error curves with various orbit altitudes

4 结 论

本文提出了一种改进的基于扩展卡尔曼滤波的脉冲星相对导航方法，选取前一时刻航天器的位置作为相对导航基准，建立了预报相位的传播模型，避免了绝对导航方式中对整周模糊度的讨论，解决了目前相对导航方案中的预报相位和标称轨道存储问题。结合典型地球轨道航天器，进行了数学仿真和导航精度分析，导航定位精度在1 km以内，能够快速抑制初始导航误差，不受轨道根数变化的影响，基本满足大多数航天器的任务需求，验证了导航方案的正确性和可行性。本文的研究作为脉冲星导航的一个新的尝试，解决了深空探测航天器导航方案中存在的参考基准的选取、导航数据的存储、导航定位解算等问题，在现有的脉冲星相对导航方案的基础上做了新的改进，为后续的研究提供了新的思路和参考。

（

）：

[1] 帅平，李明，陈绍龙，等. X射线脉冲星导航系统原理与方法[M]. 北京：中国宇航出版社，2009：16-22.

SHUAI Ping, LI Ming, CHEN Shao-long, et al. Principle and method of X-ray pulsars navigation system[M]. Beijing: China Astronautic Press, 2009: 16-22.

[2] 王超，黄显核，谢力慧. X 射线脉冲星绝对定位法研究[J]. 宇航计测技术，2010，30(4)：41-44.

WANG Chao, HUANG Xian-he, XIE Li-hui. Study of absolute position determination using X-ray pulsar[J]. Journal of Astronautic Metrology and Measurement, 2010, 30(4): 41-44.

[3] 桂先洲，黎胜亮，李志豪. 基于 X射线脉冲星绝对定位中的整周模糊度改进算法研究[J]. 国防科技大学学报，2010，32(3)：33-36.

GUI Xian-zhou, LI Sheng-liang, LI Zhi-hao. Study of betterment arithmetic of ambiguity in absolution position based on X-ray pulsar[J]. Journal of National University of Defense Technology, 2010, 32(3): 33-36.

[4] 乔黎，刘建业，郑广楼，等. XNAV 算法及其整周模糊度确定方法研究[J]. 宇航学报，2009，30(4)：1460-1465.

QIAO Li, LIU Jian-ye, ZHENG Guang-lou, et al. Study of the XNAV algorithm and the determination of the ambiguity [J]. Journal of Astronautics, 2009, 30(4): 1460-1465.

[5] 杨成伟，郑建华. XNAV/UVNAV/SINS 组合导航在航天器轨道机动中的应用[J]. 中国惯性技术学报，2012，20(2)： 200-204.

YANG Cheng-wei, ZHENG Jian-hua. XNAV/UVNAV/ SINS integrated navigation system in spacecraft orbital maneuver[J]. Journal of Chinese Inertial Technology, 2012, 20(2): 200-204.

[6] Emadzadeh A A, Speyer J L. Relative navigation between two spacecraft using X-ray pulsars[J]. IEEE Transactions on Control Systems Technology, 2011, 19(5): 1021-1035.

[7] Ray P S, Sheikh S I, Graven P H, et al. Deep space navigation using celestial X-ray sources[C]//Proc. ION 2008 National Technical Meeting. 2008: 101-109.

[8] Kim S G, Crassidis J L, Cheng Y, et al. Kalman filtering for relative spacecraft attitude and position estimation[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(1): 133-143.

[9] Munoz S, Lightsey E G. A sensor driven trade study for autonomous navigation capabilities[C]//AIAA Guidance, Navigation, and Control Conference. 2011: 08-11.

[10] Hablani H B, Tapper M L, Dana-Bashian D J. Guidance and relative navigation for autonomous rendezvous in a circular orbit[J]. Journal of Guidance, Control, and Dynamics, 2002, 25(3): 553-562.

X-ray pulsar relative navigation approach based on extended Kalman filter

XIA Hong-wei1, DIAO Yan-hua1, MA Guang-cheng1, CAO Zhuo2, WANG Chang-hong1
(1. Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin 150001, China; 2. Shanghai Aerospace Control Technology Institute, Shanghai 200233, China)

X-ray pulsar as a nature timing standard has excellent period-stability, and pulsar navigation has important application prospect. An improved relative navigation approach which selects the previous position as the navigation reference is presented to solve the integer ambiguity problem in absolute navigation and the storages problem of the phase and the nominal orbit in relative navigation. The information filtering is implied to estimate the precise relative position and velocity by stabling the orbit dynamics model. Finally, the simulations are performed, which show that the accuracy of the improved relative navigation reaches 1 km. The interferences of the initial error and the orbital elements are rapidly suppressed by the filter, which is uniformly asymptotically stabilized. The navigation program is verified to be valid and feasible.

deep space exploration; relative navigation; X-ray pulsar; extended Kalman filter

1005-6734(2014)05-0619-05

10.13695/j.cnki.12-1222/o3.2014.05.012

TL361

A

2014-05-12；

2014-08-11

国家自然科学基金资助项目（NSFC No.61304108）；上海航天科技创新基金资助项目

夏红伟（1979—），男，博士，主要从事飞行器控制及仿真技术方面的研究。E-mail：xiahongwei@hit.edu.cn

联 系 人：王常虹（1961—），男，教授，博士生导师，主要研究方向为导航、制导与控制。Email：cwang@hit.edu.cn.