基于边缘采样UKF滤波的捷联惯导初始对准方法

李方能，许江宁，亓洪标

（海军工程大学 电气工程学院，武汉 430033）

基于边缘采样UKF滤波的捷联惯导初始对准方法

李方能，许江宁，亓洪标

（海军工程大学 电气工程学院，武汉 430033）

设计了基于四元数的捷联惯导非线性初始对准模型，同时指出该模型仅仅是姿态误差四元数和速度误差的非线性函数，而对于惯性器件误差而言则是线性的。针对该模型的部分线性特性，设计了基于边缘采样的 UKF滤波算法，该算法仅对状态量中的非线性子集进行采样，因此对于部分线性模型而言，该算法在不损失滤波精度的前提下能够有效降低算法计算量。仿真及车载实测数据实验表明所研究的初始对准模型和相应的滤波算法是有效的，而且较传统方法具有明显的计算量方面的优势；在达到相同对准精度的前提下，所设计算法的计算量较传统算法降低了52%。

捷联惯导；初始对准；UKF；边缘采样

作为一种航位推算系统(Dead-Reckoning System)，捷联惯导系统初始信息直接关系到其接下来的导航定位精度[1]。因此必须为捷联惯导系统提供初始姿态、速度和位置信息，而这正是由初始对准所完成。通常情况下，初始对准一般是先进行粗对准，然后进行精对准。粗对准一般在静止条件下通过解析的方式进行，目的是获取系统粗略初始姿态信息以满足系统对姿态的小角度误差要求。小角度的姿态误差可以保证经典的惯导误差方程成立，并以此误差方程为初始对准模型进行精对准。精对准则在外部观测量的辅助下，采用最优估计的方法进行[2]。然而，在很多情况下粗对准的精度很难保证基于线性惯导误差方程精对准的小角度假设条件，这主要由于以下两个方面引起：首先在初始对准的过程中，载体可能工作在具有各种噪声的动态环境中，如系泊状态下的舰船会受到各类风浪的干扰，而作为粗对准必要条件的地球自转角速率可能被湮没在这些高频的外部干扰中，从而不能完成正常的粗对准。第二是由于捷联惯导系统的传感器性能太差。例如对于基于微惯性测量单元（MEMS）的捷联惯导系统而言，其陀螺的常值漂移一般在1～10 (°)/h之间，甚至更高，而地球的自转角速度为15 (°)/h，因此低精度陀螺仪不能有效地测得地球自转角速度，从而不能完成正常的粗对准。因此，对于低于战术级的惯导系统或是工作在恶劣动态环境下，无法实现解析式粗对准，从而不能完成传统的二阶段初始对准，必须进行非线性初始对准[3-6]。

进行非线性初始对准首先要建立非线性惯导误差方程。由于在惯导系统中姿态有不同的表示方法，如欧拉角法、方向余弦矩阵法、四元数法，因此存在不同的姿态误差方程，其中欧拉角法因其物理意义明确、误差方程推导直接而得到广泛的应用。建立基于欧拉角误差方程首先需要确定导航坐标系和计算导航坐标系之间的方向余弦矩阵，此方向余弦矩阵的建立是通过三个轴向以失准角顺序旋转得到的。然而在大失准角条件下，不同的旋转顺序得到的方向余弦矩阵是不同的，而传统方法都是采用某一特定旋转次序，因此大失准角条件下的欧拉角误差方程是不严格的。四元数相对于欧拉角具有以下突出优点：第一，不存在奇异性；第二，姿态矩阵可表示为四元数的代数形式；第三，在大角度条件下，基于四元数建立的姿态矩阵不涉及具体转动次序[7-8]。因此，本文拟建立基于四元数来的大失准角姿态误差方程用以非线性初始对准。

无味卡尔曼滤波（unscented Kalman filter, UKF）因其精度、计算量、适应性等方面的突出优点，在实际系统中得到了越来越广泛的应用[9-10]。由于非线性初始对准模型是一个高维模型，将UKF应用到非线性初始对准中会产生较大的计算负担，从而影响其实时应用[3-4]。对于UKF算法而言，影响其计算量的核心是sigma点采样计算。为了减小UKF算法的计算量，Julier设计了不同的简化UKF算法，但是他所设计的简化UKF算法都是以牺牲滤波精度为前提的，而且是通用方法，并未考虑具体实际应用模型。在捷联惯导初始对准问题中陀螺漂移一般都是假设为常值误差来进行估计，因此其对应的状态方程是线性的，从这一点来讲我们所研究的姿态估计模型是部分线性的。因此能否考虑只对模型中的非线性状态部分使用 UKF算法而对线性部分使用卡尔曼滤波算法，以期达到不损失滤波精度的前提下减小算法计算量的目的[6,11-14]。本文拟从边缘概率密度的角度对该问题展开研究，分析指出基于四元数的非线性初始对准模型本质上是部分线性模型，其中的姿态误差四元数和速度误差是非线性函数。本文将基于边缘采样的无味变换（unscented transformation, UT）应用到该问题中。仿真及实测数据实验表明，所研究算法在不损失滤波精度的前提下，能够有效降低算法计算量，因此特别适合于实时应用。

1 基于四元数的非线性对准模型

记惯性坐标系为i系，地理坐标系（或导航坐标系）为n系，地球坐标系为e系，载体坐标系为b系；同时为了推导对准误差模型，引入计算导航坐标系n′系。

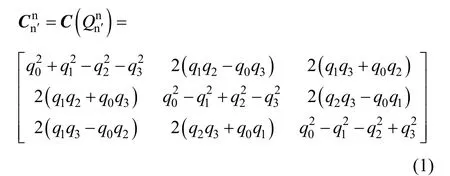
1.1 捷联惯导误差模型

当不考虑任何误差时，速度的理想值由下式确定：

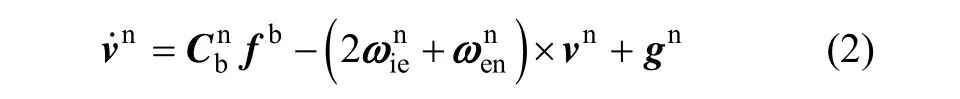
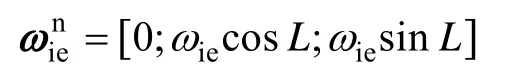
在实际系统中由于存在各种外界干扰和误差，真实的速度方程为：

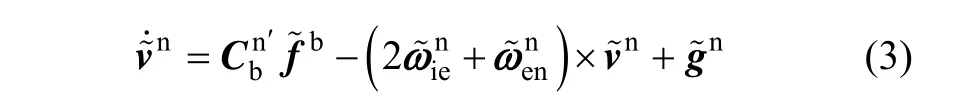
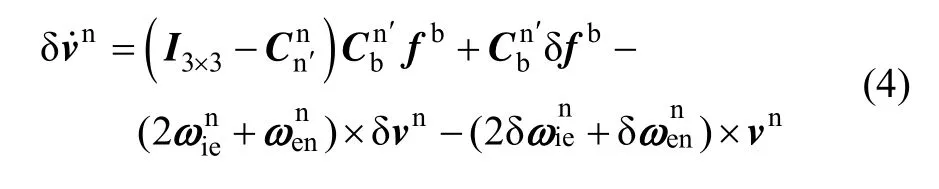
式中，I3×3表示3维单位矩阵，δL和δh分别为纬度和高度误差，具体表达式将在后文给出。在计算式(3)时忽略了重力矢量误差。在初始对准过程中加速度计的误差一般只考虑常值零偏▽b以及随机噪声，因此公式(4)中的 δfb可以用▽b替代。式(1)～(4)中的可以写成式(1)中的四元数形式，因此式(4)可进一步表示为：

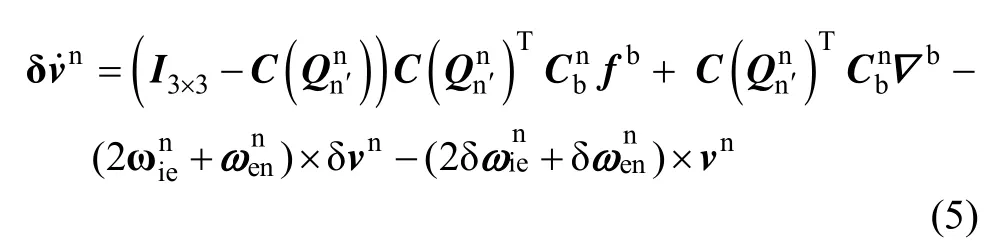
理想情况下，基于四元数的载体姿态运动学方程为：

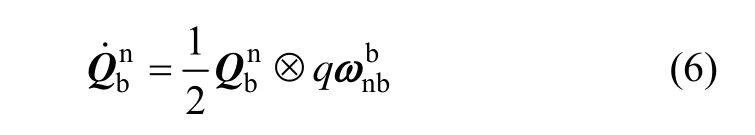
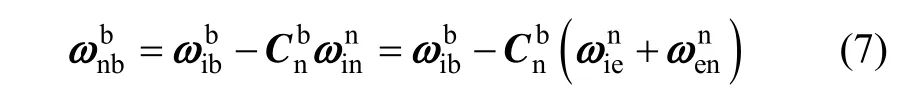
由于外界的各种干扰及器件误差，真实的姿态四元数运动学方程为：

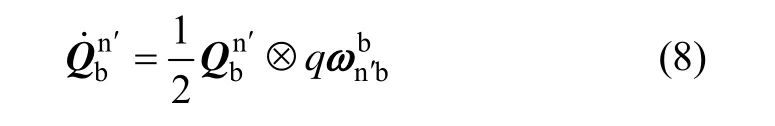
式中，

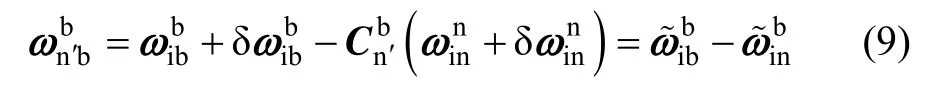
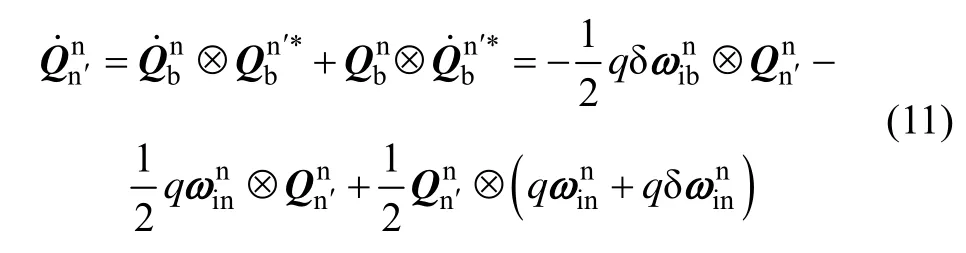
式(11)中第二行到第三行的计算过程考虑了如下关系式：

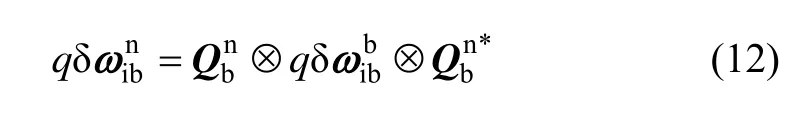
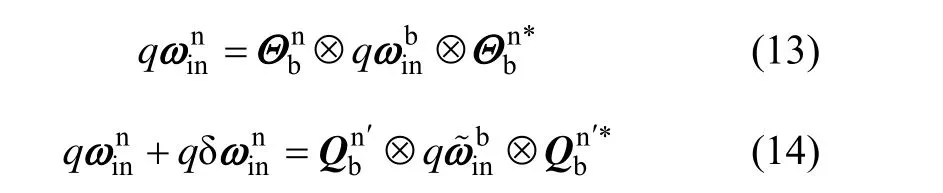
在初始对准过程中陀螺仪的器件误差一般只考虑陀螺漂移 εb和随机游走，因此式(11)中的可以用代替：

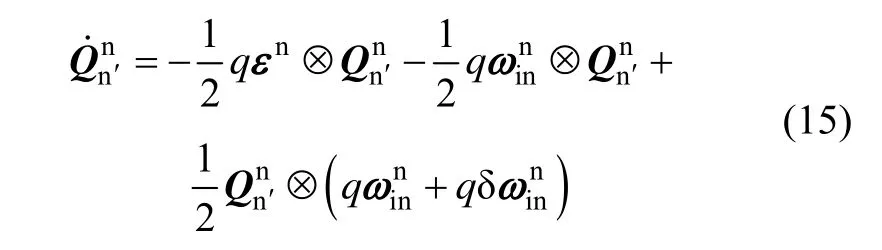
1.2 非线性初始对准滤波模型

在初始对准过程中一般需要对陀螺仪漂移和加速度计零偏进行估计补偿，因此需要建立相应的状态方程，具体形式如下：

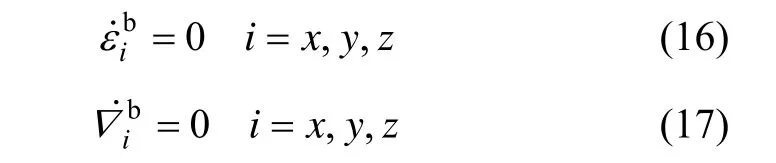
选取系统状态为：

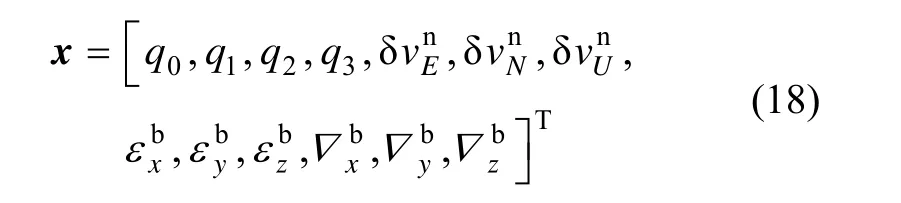
结合捷联惯导的非线性误差方程，可得到任意失准角条件下初始对准的系统方程为：

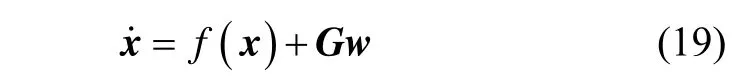
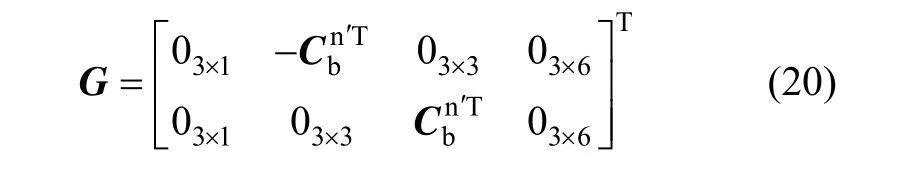
f（x）由式(5)(15)～(17)所确定，其紧凑形式为：

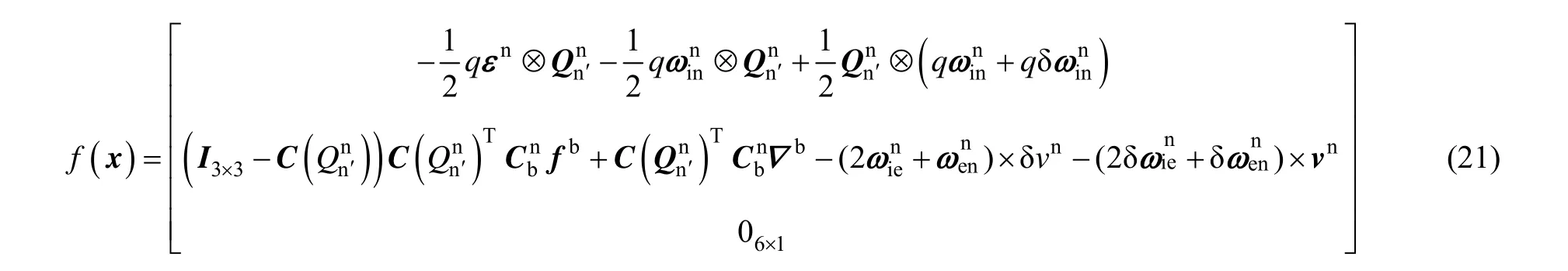
式(18)中所选的状态是一种一般形式的量，具体使用时可根据应用场合进行相应简化，如对于路用及海用捷联惯导，天向速度分量及对应的加速度计常值零偏分量可以忽略。

在实际应用中一般选取速度误差作为系统观测量，即

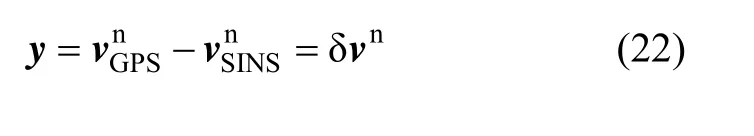
2 非线性初始对准模型的部分线性框架

式(21)中的模型是非线性的，因此需要采用非线性滤波算法进行状态估计。一般而言，非线性滤波算法都是将状态看成一个整体，只要状态中任意一子集是非线性的，则将整个状态模型整体看成是非线性的。但是通过仔细分析可以发现，很多实际应用的非线性模型仅仅是状态中某一子集的非线性函数，而对于其它子集而言则是线性的，对于这类模型我们一般称之为部分线性模型。下面我们将分析指出式(21)中所存在的部分线性框架。

假设惯导更新的时间间隔为dt，则式(21)对应的离散形式为：

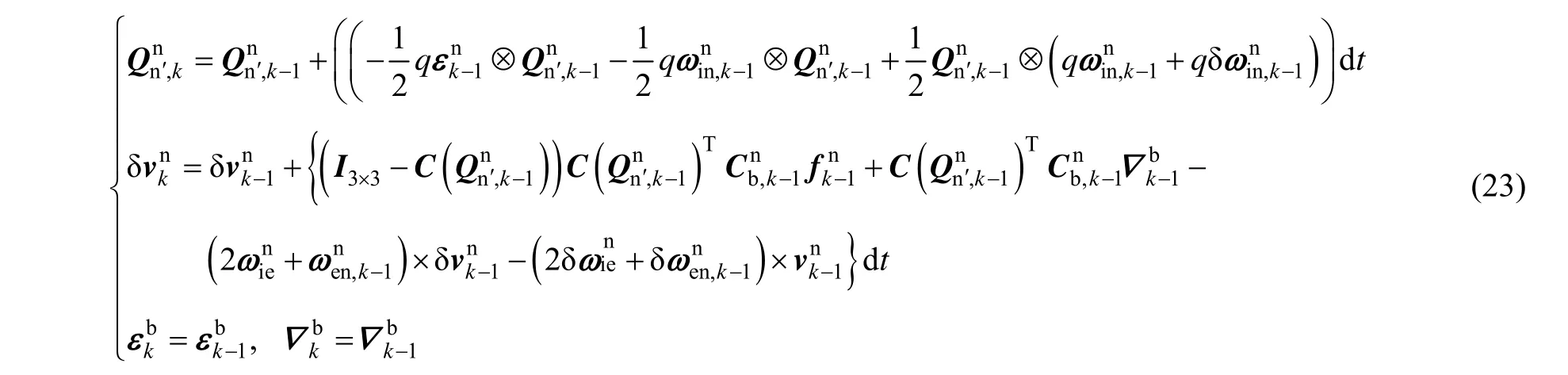
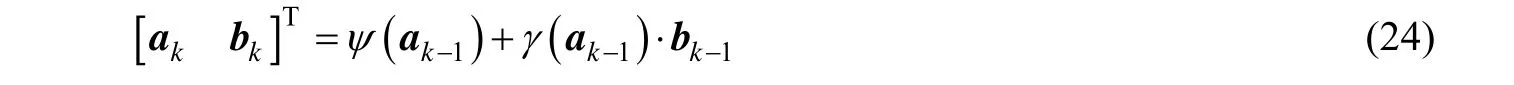
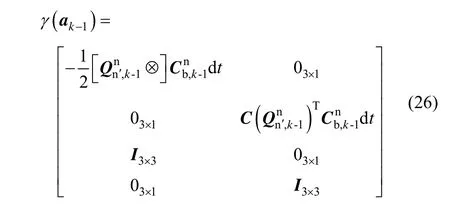
从式(25)可以看出，基于四元数的非线性初始对准模型仅仅是姿态误差四元数和速度误差的非线性函数，对于惯性器件误差而言则是线性的。对于这种部分线性模型，可以通过边缘概率密度的概念设计相应的简化滤波算法，下节将给出基于UKF的简化算法。

3 基于边缘采样的简化UKF算法设计

对于部分线性系统，我们可以考虑只对状态中非线性部分的状态采样UKF滤波，而对线性部分则直接应用卡尔曼滤波。此处我们引入边缘无味变换的概念（Marginalized unscented transform, MUT）用以解决该类问题。

对于一状态量x，其可分解为非线性和线性两部分，即 x =[aT,bT]T，那么一部分线性函数g是指它可写为如下形式：

式中， x ∈Rn， g(·)是任意一非线性函数，它可以是状态方程，也可以是量测方程； a ∈Rna， b∈Rnb并且na+ nb= n；ψ是a的非线性函数；γ是a的函数，可以是线性，也可以是非线性。在常规的UKF算法中，该类问题需要对全状态进行sigma点采样，即在每一步滤波中计算2 n+1个sigma点。考虑到该类问题在模型上的特殊性，我们可以引入边缘概率密度的思想，只对其中非线性部分进行采样，即每一步滤波中只需要计算2 na+1个sigma点，而且这种方法不损失滤波算法的精度。下面我们简要给出基于边缘概率密度思想的MUT算法流程。

假设状态服从高斯分布如下：

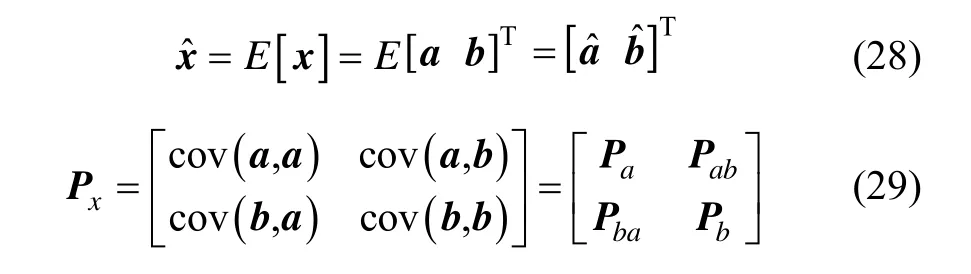
根据高斯分布的特性及矩阵运算法则可得：

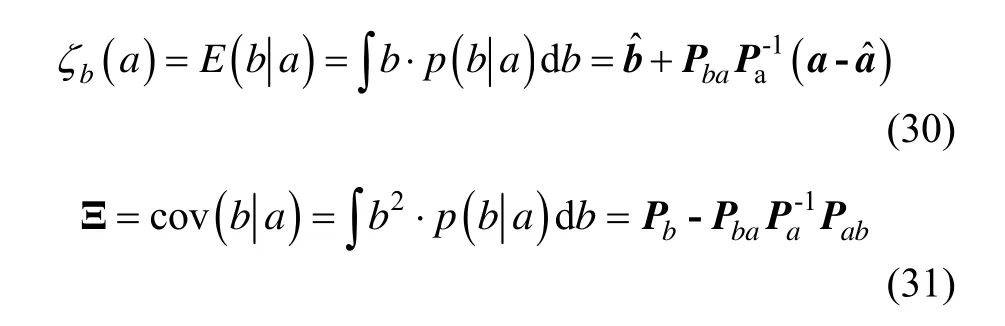
那么传递后的均值可通过下式计算：

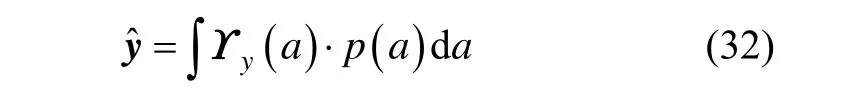
式中，

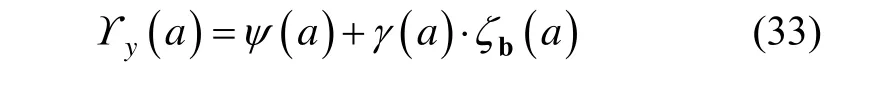
对于式(32)中的问题我们可以采用常规 UT算法计算其均值。由式(32)我们可以计算状态非线性部分a对应的sigma点极其均值：

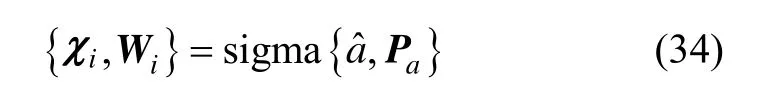
具体采样方法可参考Julier相关文献。那么经式(32)传递后的sigma点为：

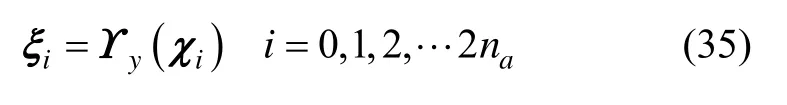
由UT算法可得传递后的均值和方差分别为：

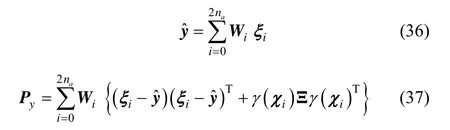
从上面的算法流程可以看出，在MUT算法中只需要对状态的非线性部分进行采样，因此可以有效降低算法计算量。具体到惯性系初始对准问题中，只需要对姿态和速度部分进行采样，则相应的计算量可降低50%。将MUT替换传统UKF中的UT即可得到基于边缘采样的简化UKF算法（MUKF），该过程比较直接，具体过程此处不再给出。

4 实验验证

4.1 仿真实验

为验证算法的有效性，设计了静基座条件下的仿真实验。仿真实验中使用的惯性器件精度分别如下：陀螺随机常值漂移为 0.01 (°)/h，陀螺白噪声为 0.03 (°)/h，加速度计随机常值零偏为100 μg，加速度计量测白噪声为500 μg。速度量测噪声为0.01 m/s。滤波时间步长取为0.1 s，仿真总时间长度为600 s，并对惯导的速度、姿态进行反馈校正。对准精度用惯导反馈校正后的姿态与真实姿态的误差进行评估。实验中方位失准角服从[0°60°]上的均匀分布，两个水平失准角服从 [- 15°15°]上的均匀分布。进行100次蒙特-卡洛仿真实验并计算三个失准角的平均估计误差和对应的3σ，结果分别如图1～图3所示。图中红线表示UKF，蓝线表示MUKF；实线表示均值，虚线表示均方差。从图中可以看出，两种方法的精度基本相当，而且都能实现对较大初始失准角的有效估计，估计误差均值在对应的3σ内，从而说明相应的算法是有效的。同时本文针对非线性初始对准模型设计的 MUKF算法由于在每次滤波中只需要传统 UKF算法的接近一半数量的sigma点，因此计算量仅仅为传统算法的50%。

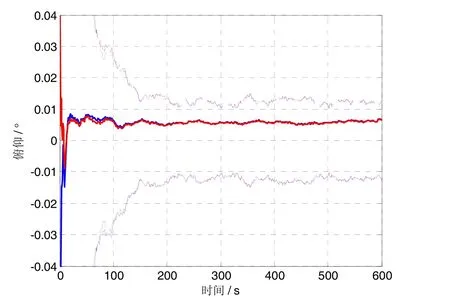
图1 俯仰角估计误差Fig.1 Estimation error for the pith angle

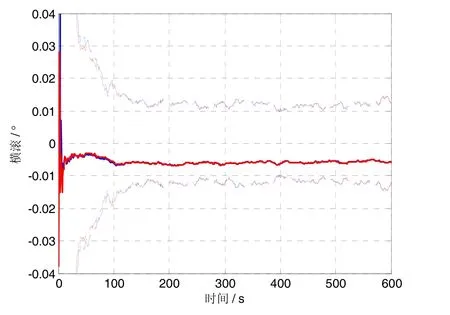
图2 横滚角估计误差Fig.2 Estimation error for the roll angle

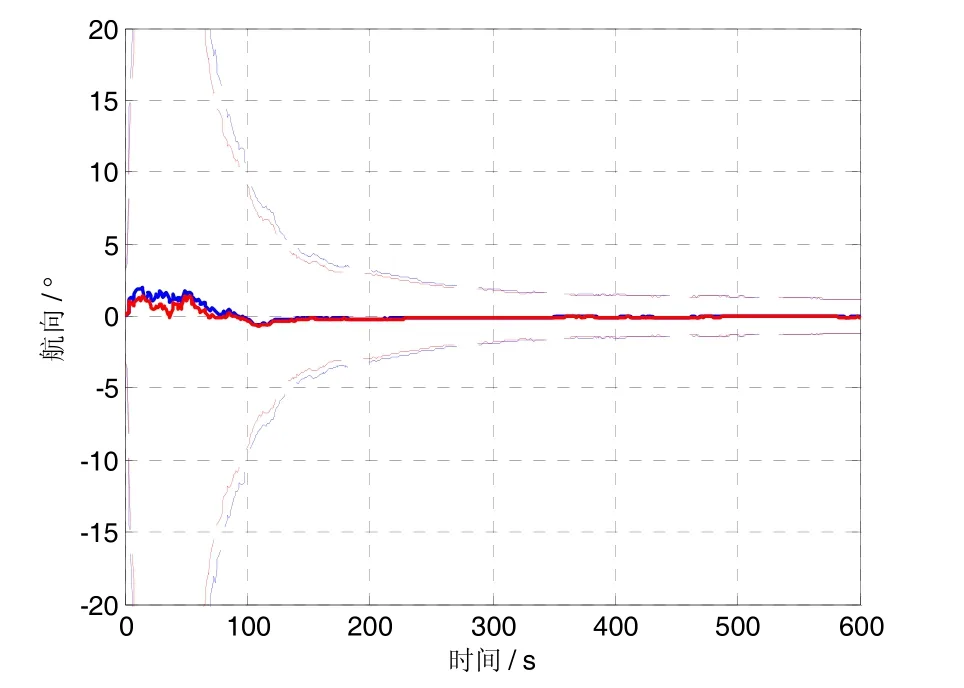
图3 航向角估计误差Fig.3 Estimation error for the yaw angle

4.2 车载实验

为了进一步验证所研究算法的有效性，设计了相应的车载实验。实验设备主要包括激光捷联惯导、里程计、GPS接收机等，其中激光陀螺漂移约为 0.007 (°)/h，加速度计零偏约为 5×10-5g，捷联惯导的更新率为125 Hz；GPS更新率为1 Hz。实验中选取300 s的车载数据进行初始对准算法验证。300 s实验数据对应的姿态基准如图4所示。

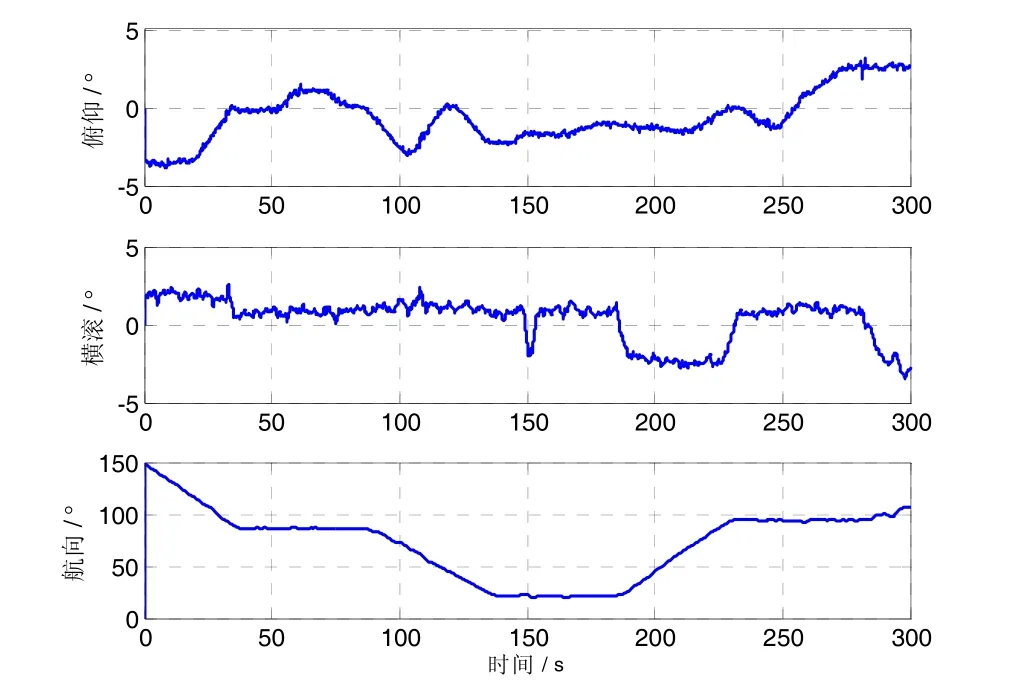
图4 车载对准实验参考姿态Fig.4 Reference attitude in the experiment

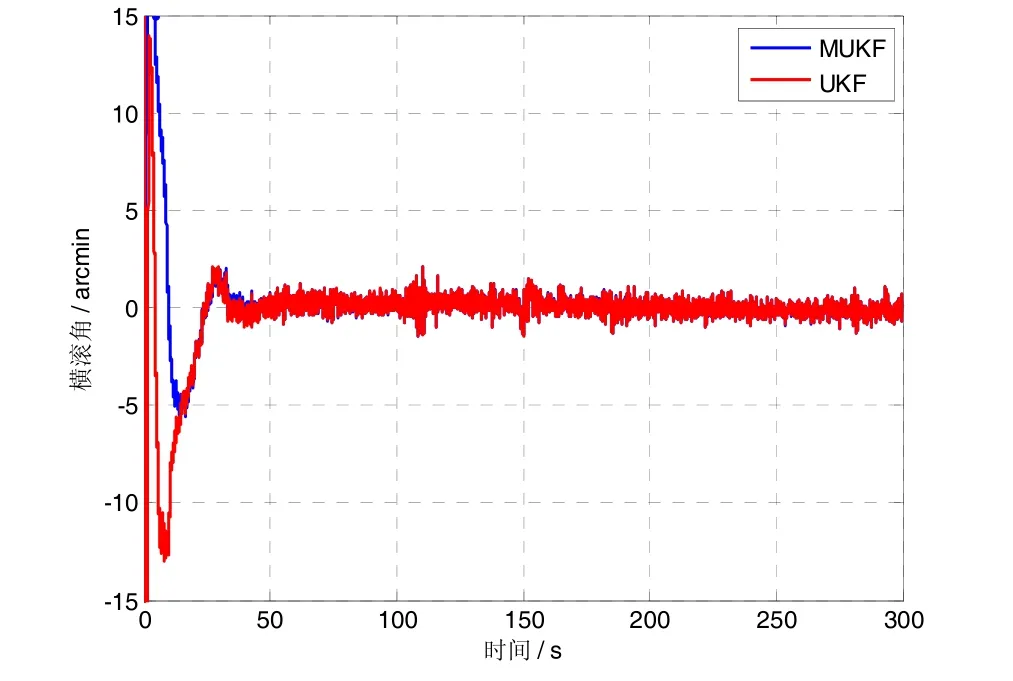
图6 横滚角估计误差Fig.6 Estimation error for the roll angle

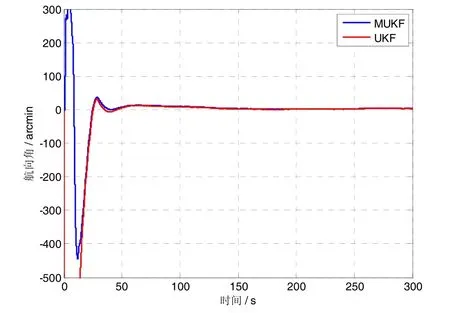
图7 航向角估计误差Fig.7 Estimation error for the yaw angle

5 结 论

研究了基于四元数的非线性初始对准问题，分析指出了基于四元数的非线性初始对准模型本质上是一部分线性模型，即该模型仅仅是姿态误差四元数和速度误差的非线性函数，而对于器件误差而言则是线性的。针对该模型的这一特性，设计了一种基于边缘采样的UKF滤波算法，该算法只对部分线性模型中状态的非线性子集进行采样，在不损失滤波精度的前提下能够有效降低算法计算量。仿真实验及车载实测数据实验表明该算法能够达到传统 UKF滤波算法相同的滤波精度，但是计算量几乎降低52%。

（

）：

[1] Titterton D H, Weston J L. Strapdown inertial navigation technology[M]. 2nd Edition. London: the Institute of Electrical Engineers, 2004.

[2] 刘锡祥，徐晓苏，李天旦，刘义亭，王立辉. 基于数据存储与循环解算的 SINS 快速对准方法[J]. 中国惯性技术学报，2013，21(6)：715-720.

LIU Xi-xiang, XU Xiao-su, LI Tian-dan, LIU Yi-ting, WANG Li-hui. Fast alignment method for SINS based on stored data and loop calculation[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 715-720.

[3] 严恭敏，严卫生，徐德民. 简化 UKF 滤波在 SINS 大失准角初始对准中的应用[J]. 中国惯性技术学报，2008，16(3)：253-264.

YAN Gong-min, YAN Wei-shen, XU De-min. Application of simplified UKF in SINS initial alignment for large misalignment angles[J]. Journal of Chinese Inertial Technology, 2008, 16(3): 253-264.

[4] Zhou Ben-chun, Cheng Xiang-hong. Robust UKF algorithm in SINS initial alignment[J]. Journal of Southeast University (English Edition), 2011, 27(1): 56-60.

[5] Ali J. Initial orientation of inertial navigation system realized through nonlinear modeling and filtering[J]. Measurement, 2011, 44: 793-801.

[6] Chang Lu-bin, Hu Bai-qing, Li An, Qin Fang-jun. Strapdown inertial navigation system alignment based on marginalized unscented Kalman filter[J]. IET Science, Measurement and Technology, 2013, 7(2): 128-138.

[7] 房建成，韩晓英，杨凤英.一种高精度机载POS双位置对准方法[J]. 中国惯性技术学报，2013，21(3)：318-323.

FANG Jian-cheng, HAN Xiao-ying, YANG Feng-ying. Two-position alignment method of airborne position and orientation system[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 318-323.

[8] 夏家和，秦永元，赵长山. 适用于低精度惯导的非线性对准方法研究[J]. 仪器仪表学报，2009，30(8)：1618-1622.

XIA Jia-he, QIN Yong-yuan, ZHAO Chang-shan. Study on nonlinear alignment method for low precision INS [J]. Chinese Journal of Scientific Instrument, 2009, 30(8): 1618-1622.

[9] Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation[J]. Proc. IEEE, 2004, 92(3): 401-422.

[10] Chang Lu-bin, Hu Bai-qing, Li An, Qin Fang-jun. Transformed unscented Kalman filter[J]. IEEE Transactions on Automatic Control, 2013, 58(1): 252-257.

[11] Chang Lu-bin, Hu Bai-qing, Chang Guo-bin, Li An. Marginalized iterated unscented Kalman filter[J]. IET Control Theory & Applications, 2012, 6(6): 847-854.

[12] Morelande M R, Ristic B. Smoothed state estimation for nonlinear Markovian switching systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(4): 1309-1324.

[13] Chang Guo-bin. Marginal unscented Kalman filter for crosscorrelated process and observation noise at the same epoch [J]. IET Radar, Sonar and Navigation, 2013, 8(1): 54-64.

[14] Chang Guo-bin. Loosely coupled INS/GPS integration with constant lever arm using marginal unscented Kalman filter[J]. The Journal of Navigation(in press). doi: 10.1017/S0373463313000775.

Initial alignment of strapdown inertial navigation system based on marginalized unscented Kalman filter

LI Fang-neng, XU Jiang-ning, QI Hong-biao
(Department of Electrical Engineering, Naval University of Engineering, Wuhan 430033, China)

A quaternion-based nonlinear model is designed for the initial alignment of a strapdown inertial navigation system(SINS) with large initial errors. It is pointed out that the model has only the nonlinear function relation with quaternion-based misalignment error and the velocities error, whereas it has linear relation with the errors of inertial sensors. In view of this partially linear characteristic, a unscented Kalman filter(UKF) algorithm with marginalized-sampling-based unscented transformation(UT) is designed, which only samples the nonlinear subset of state variables, and can effectively reduce the computation burden without losing filtering accuracy. Simulations and car-mounted experiments demonstrate that the marginalized UT-based Kalman filter can achieve at least a comparable performance to the traditional UT-based Kalman filter with a significantly lower expense. Compared with the traditional algorithm, the investigated method can reach the same alignment precision but with 52% reduced computational burden.

SINS; initial alignment; unscented Kalman filter; marginalized sampling

联 系 人：许江宁（1964—），男，教授，博士生导师。E-mail：xujiangning@hotmail.com

1005-6734(2014)05-0612-07

10.13695/j.cnki.12-1222/o3.2014.05.011

U666.1

A

2014-05-14；

2014-09-17

国家自然科学基金（61304241，61374206）

李方能（1978—），男，讲师，从事惯性技术及应用研究。E-mail：leefangneng@163.com