基于稀疏高斯积分的舰机传递对准滤波方法
2014-10-24穆荣军王丹丹乔立伟
梁 浩,穆荣军,王丹丹,蔡 玲,乔立伟
(1. 哈尔滨工业大学 航天学院,哈尔滨 150001;2. 北京宇航系统工程研究所,北京 100076;3. 天津航海仪器研究所,天津 300131)
基于稀疏高斯积分的舰机传递对准滤波方法
梁 浩1,穆荣军1,王丹丹2,蔡 玲3,乔立伟3
(1. 哈尔滨工业大学 航天学院,哈尔滨 150001;2. 北京宇航系统工程研究所,北京 100076;3. 天津航海仪器研究所,天津 300131)
针对舰机传递对准中的大姿态失准角问题,研究了稀疏高斯厄米特积分滤波在舰机传递对准中的应用。为了解决稀疏高斯滤波中积分点利用效率不高的问题,提出了一种改进的自适应各向异性稀疏高斯积分滤波算法,改进算法根据状态参数可观测度大小将积分变量分类并根据分类结果构造各向异性权重向量来控制各维通道积分的精度等级,进而对各变量通道的积分点数目进行合理分配。模拟轨迹下仿真结果表明,采用稀疏高斯滤波与采用改进算法的舰机传递对准精度相当,较无味卡尔曼滤波有所提高,对准精度由3′提高到2′;改进算法的积分点数目减少了30%~60%,提高了计算效率。
舰载机;传递对准;非线性滤波;可观测度;各向异性;高斯厄米特
舰载机着舰后在甲板上停放的位置是随机的,利用着舰后机载惯导关机时刻的导航信息,能够得到舰载机相对舰船基准粗略的姿态关系,进而在下次值机起飞前通过传递对准获得机载惯导准确的初始姿态信息。通常认为上次着舰后飞机惯导的姿态角误差为小量,在小失准角条件下推导出惯导系统的线性误差传播方程[1-2]。然而,实际中经常会出现大初始失准角的情况,近年来,许多学者对大姿态失准角下的非线性模型及非线性滤波算法开展了大量研究[3-5]。
在非线性滤波算法方面,扩展卡尔曼滤波(Extended Kalman Filter,EKF)应用最为广泛,EKF利用一阶泰勒近似将非线性模型线性化,但EKF计算过程复杂,当遇到强非线性模型时误差较大。无味卡尔曼滤波采用UT变换近似非线性函数的概率密度,具体采样形式为确定性采样,理论上UKF能以二阶或三阶精度计算后验分布的均值和协方差[6-7]。高斯厄米特积分滤波(Gauss-Hermite Quadrature Filter,GHQF)利用高斯厄米特积分方法来直接处理非线性模型,研究表明[8],GHQF的估计精度高于EKF和UKF。但GHQF的积分点数目随着变量维数的增加呈指数形式增长,为了解决GHQF的维数灾难问题,有学者提出了稀疏网格积分滤波方法,其原理是利用Smolyak法则来减少积分采样点,SGHQF采样点的个数随着系统维数的增加仅呈多项式形式增长,SGHQF在收敛速度和估计精度方面优于EKF和UKF,与GHQF相比,SGHQF具有更高的计算效率[9-10]。
本文建立了大姿态失准角下惯导系统误差传播模型,将SGHQF算法应用于舰机传递对准,为了进一步降低实际应用中SGHQF的计算负担,提出了一种基于系统状态参数可观测度分析的自适应各向异性稀疏积分滤波算法,并采用模拟轨迹对基于改进方法的舰机传递对准进行了仿真验证。
1 自适应各向异性稀疏积分滤波算法
稀疏网格Smolyak规则是对单变量GHQ积分进行多维扩展的一种方法,描述如下:
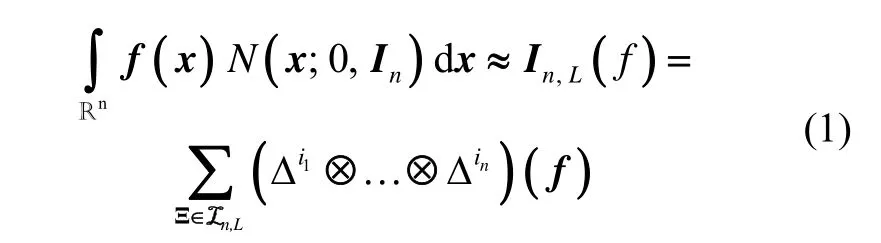
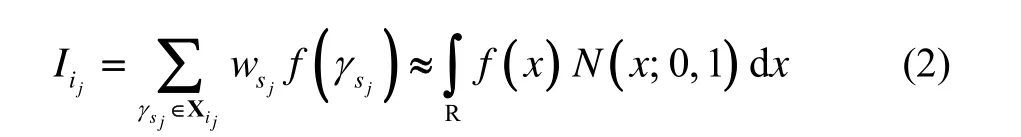
式中, wsj、γsj为 ij精度等级的单变量积分权值和积分点。
SGHQF积分点的数目随着积分变量维数的增加呈多项式增长,降低了计算量。然而,SGHQF对各维积分变量同等重视,均匀分配积分点,因此,SGHQF的积分点利用效率并不是最高的。滤波器的估计速度和精度取决于系统的可观测性,状态分量可观测性的强弱用可观测度来衡量。下面给出改进的AASGHQF算法,该算法根据各通道变量的可观测度大小对各积分变量进行分类,以此来分配各维积分点数目,将更多积分点分配至更重要的变量通道[11]。表达式如下:
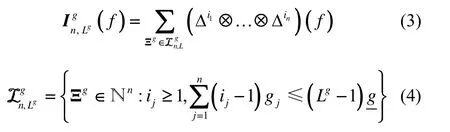
可观测度的分析方法主要有估计误差协方差阵的征值法和可观测矩阵的奇异值分解法,前者要在Kalman滤波运算之后才能进行可观测度分析,而后者可以在滤波估计的同时进行可观测度计算。利用微分几何非线性系统理论及李导数对非线性系统进行可观测性分析并求解非线性系统的可观测矩阵[12],采用奇异值分解法(Singular Value Decomposition,简称SVD法)对系统状态分量的可观测性进行定量分析[13]。状态分量的可观测度定义为:

式中:ηj表示状态向量中第j个分量的可观测度,σ0表示外观测量所对应的奇异值,σmax为使待估计的初始状态取得最大值的奇异值。
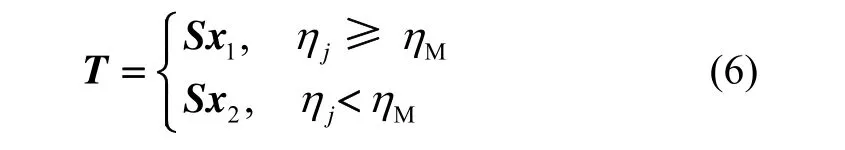
在进行集合划分时,要求各子集之间互不相交。经上述筛选处理后,S x (n)中所有状态分量按可观测度强弱划分到高-低( Sx1和 Sx2)两个子集中。通过计算各变量通道的可观测度大小对g进行赋值,对于可观测度低的变量通道,即使非线性程度较大,也应减少其积分点数目所占的比重,合理有效地对积分点进行分配。
式(3)可改写为:
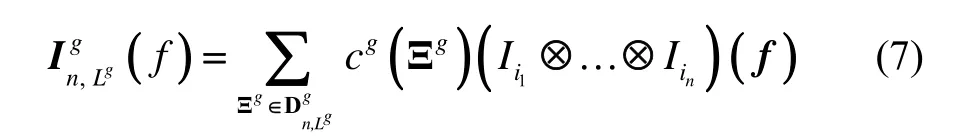
式中:
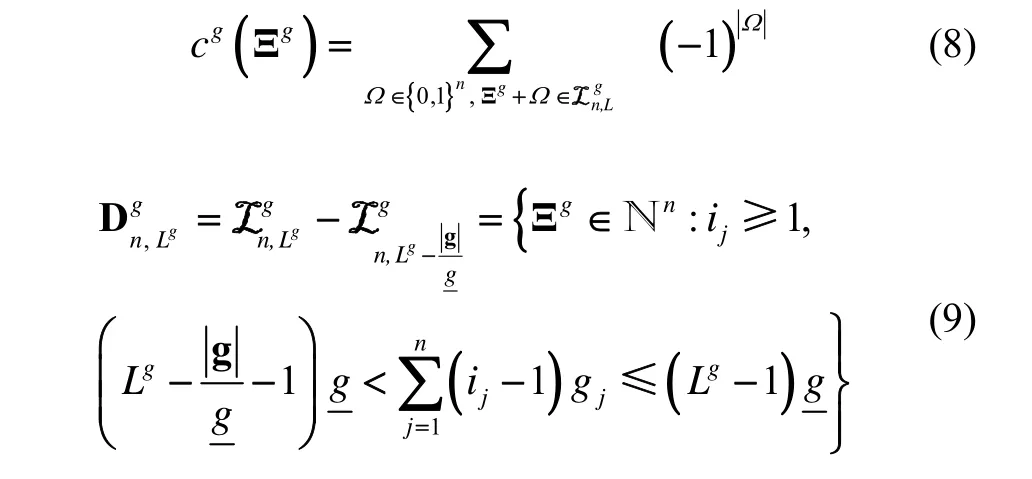
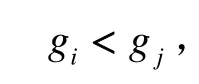
AASGHQ的积分点可表示为:
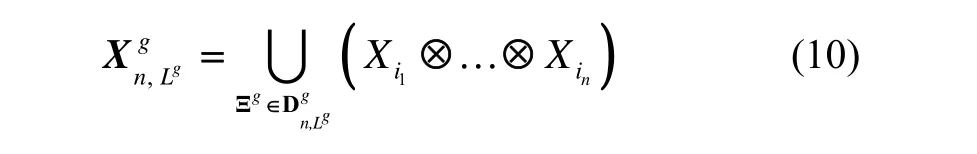
2 地理系下舰机传递对准模型
2.1 惯导非线性误差传播模型
舰机传递对准过程中,涉及到主、子两套惯性导航系统,其误差传播特性同单个惯导系统的误差传播特性有一定差异,需要对相关参量进行重新定义和处理,当姿态失准角为大角度时,基于小角度假设的一阶线性化惯导误差方程不能准确描述系统的误差传播特性,应建立大失准角下的非线性系统模型。
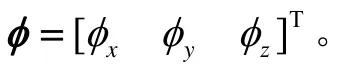
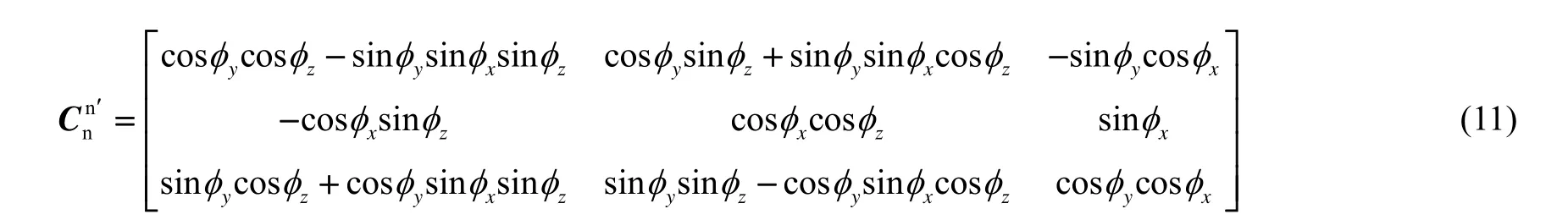
地理坐标系内,捷联惯导系统的非线性误差传播模型为[14]:
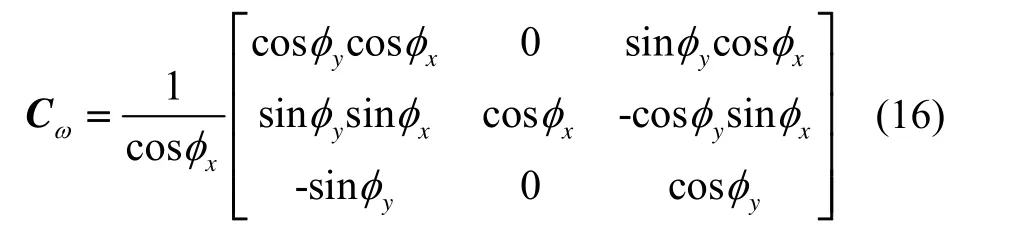
2.2 传递对准模型
2.2.1 状态方程
取状态向量为:
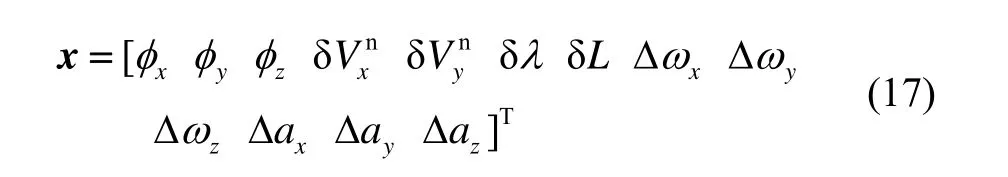
式中:各分量依次分别为姿态失准角、主子惯导东向及北向速度之差、经纬度之差、子惯导的陀螺常值漂移和加速度计测量零偏。
系统的非线性状态方程为:
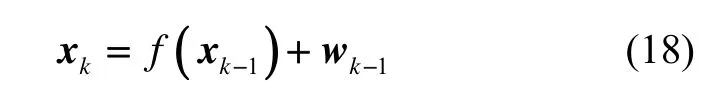
式中:f为非线性向量函数, wk-1为零均值高斯白噪声序列,其方差阵为 Qk-1。
2.2.2 观测方程
采用速度匹配模式,系统的观测向量为:
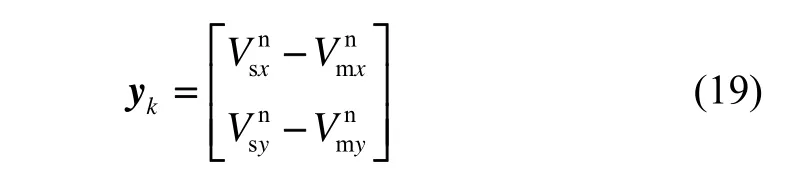
观测方程为:
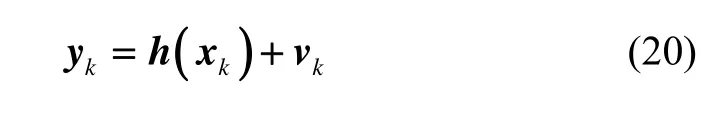
2.3 滤波器设计
舰机传递对准系统的概率密度为高斯型,传递对准滤波器具有如下形式。
1)预测:
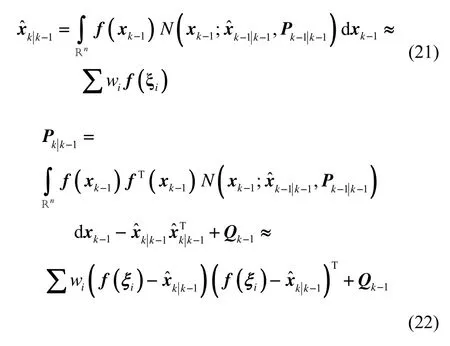
2)更新:
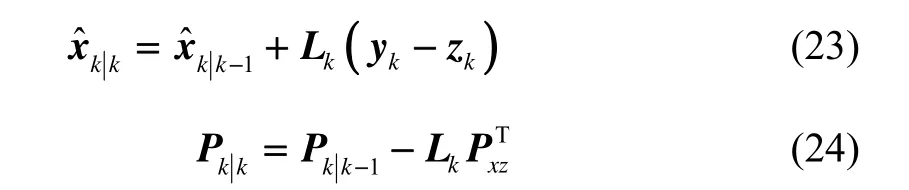
式中:
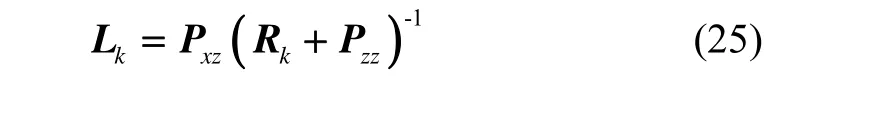
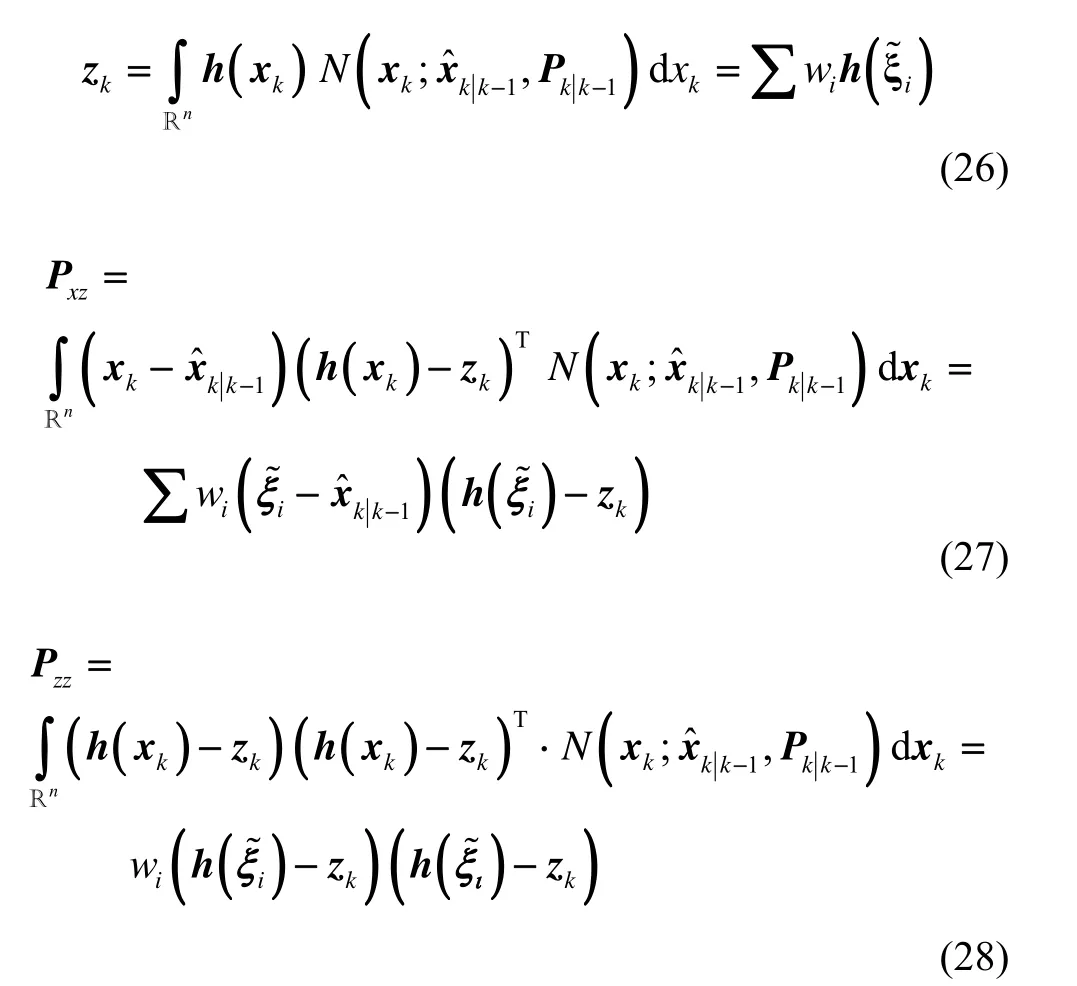
3 仿真分析
3.1 仿真分析1
选取精度等级为 3的二维高斯积分进行仿真分析,对SGHQ和AASGHQ的积分点数目和分布进行比较。L精度等级的单积分点的数目为2L-1个[15],分别用 X1、 X2和 X3表示等级1、2、3的单变量积分点,则 X1、 X2和 X3包含的积分点分别为1、3、7个。根据稀疏网格积分规则,SGHQ的积分点为D2,3= {(1,1),(1,2),(1,3),(2,1),(2,2),(3,1),},取点分布如图 1所示[10]。当 g= [2,1]时,根据式(7)~(10)得 AASGHQ的积分点为 D2,3= {(1,1),(1,3),(2,1)},取点分布如图2所示。
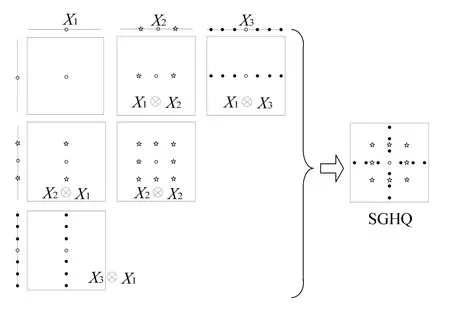
图1 SGHQ取点分布示意图Fig.1 Points distribution of SGHQ
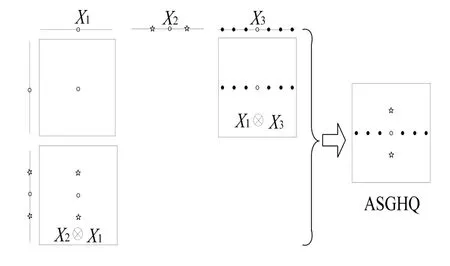
图2 AASGHQ取点分布示意图Fig.2 Points distribution of AASGHQ
当L=3,n=1~6时,SGHQ、AASGHQ的积分点数如表1所示,AASGHQ需要更少的积分点。
由计算结果可以看出,g的取值决定了各维积分ij的幅值范围及积分点的数目。可以根据式(5)、式(6)的可观测度分组计算依据对g进行赋值。AASGHQF与SGHQF相比,AASGHQF能够减少30%~60%的积分点数。
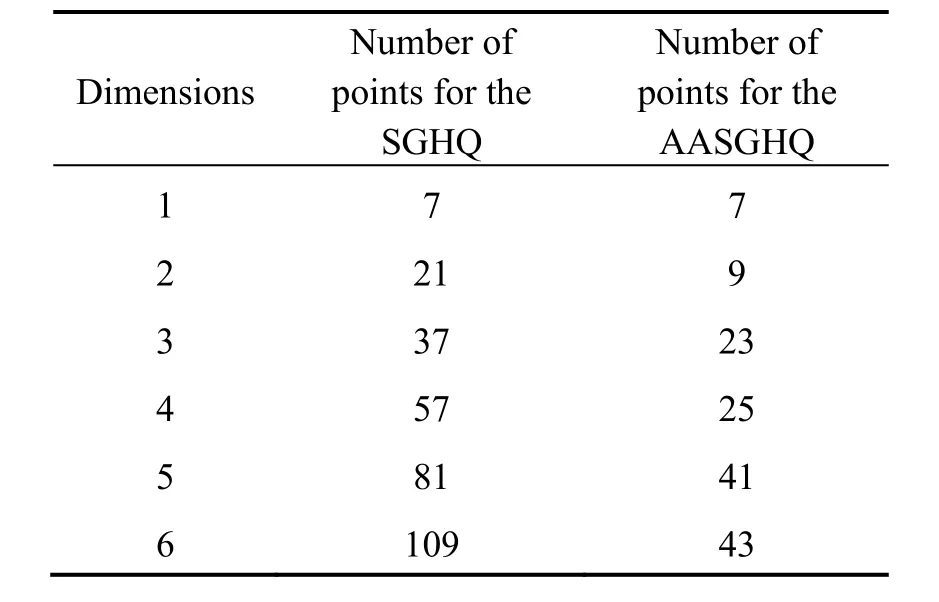
表1 SGHQ和AASGHQ所需积分点的数目Tab.1 Number of points of SGHQ and AASGHQ
3.2 仿真分析2
采用模拟轨迹分别对基于 UKF、SGHQF和AASGHQF的舰机传递对准进行仿真对比分析。
在二级海情下,舰船以10 m/s的速度做匀速直线运动,主惯导陀螺常值漂移0.0012 (°)/h(1σ),加表零偏6×10-6g(1σ);子惯导陀螺常值漂移0.06 (°)/h(1σ),加表零偏3×10-4g(1σ);主、子惯组数据更新周期为0.1 s,传递对准滤波周期为0.2 s,仿真时间15 min;舰体坐标系内横向、法向和纵向杆臂为[2m 6.7m 35m],预设安装误差角和甲板静态变形角之和为1.0°;SGHQF、AASGHQF的精度等级均取为L=3;AASGHQF中g根据可观测度计算结果进行取值,对可观测度低的变量通道积分点进行稀疏,ηM取值为1。
模拟飞行轨迹下系统各状态分量的可观测度计算结果如表2所示(选取其中一段),相应的自适应重要度因子的取值为g=[1, 1, 2, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2]。
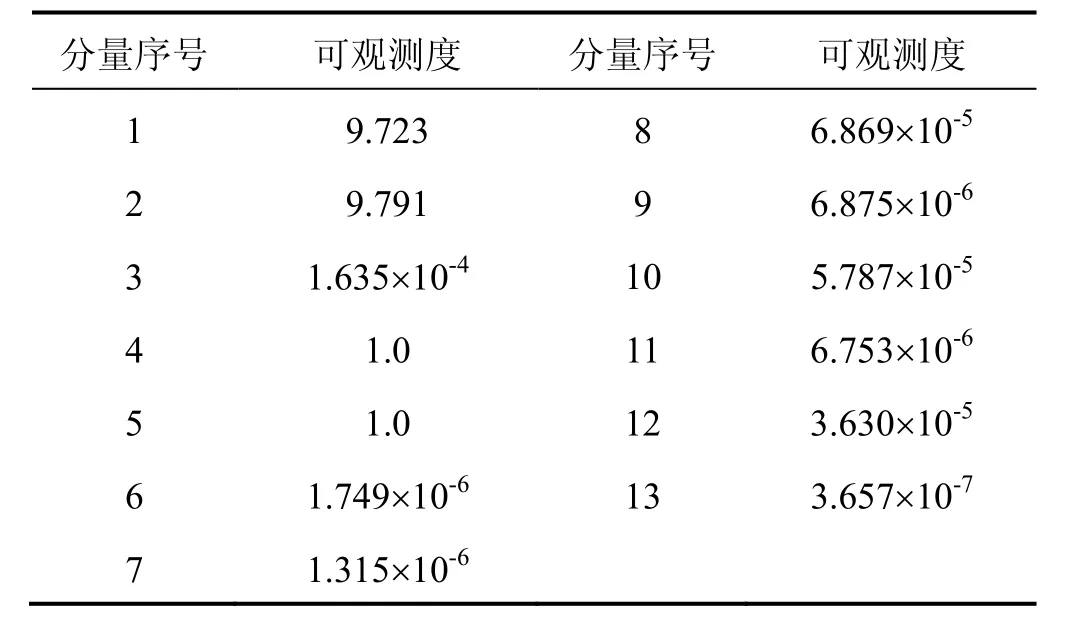
表2 模拟轨迹下状态参数可观测度Tab.2 Observable degree of state parameters under simulation trajectory
采用舰船模拟轨迹,基于 UKF、SGHQF和AASGHQF的惯导传递对准结果如图3和图4所示。
基于三种非线性滤波算法的传递对准估计精度对比如表3所示,表中Δφ为姿态失准角估计误差,ΔV为速度估计误差。

表3 仿真结果对比Tab.3 Comparison of simulation results
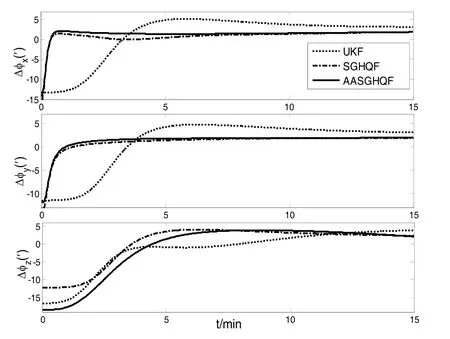
图3 姿态失准角估计误差Fig.3 Estimation error of misalignment angles
由仿真结果图3、图4和表3可以看出,与基于UKF的传递对准相比,采用AASGHQF和SGHQF方法时,能够减小三向姿态失准角和速度的估计误差,对准精度提高了1′;AASGHQF与SGHQF两者滤波估计精度相当,根据AASGHQF和SGHQF计算量分析结果可知,由于采用了各向异性稀疏算法,基于AASGHQF的舰机传递对准在保证对准精度的同时,所需的积分点数目更少,计算效率更高。
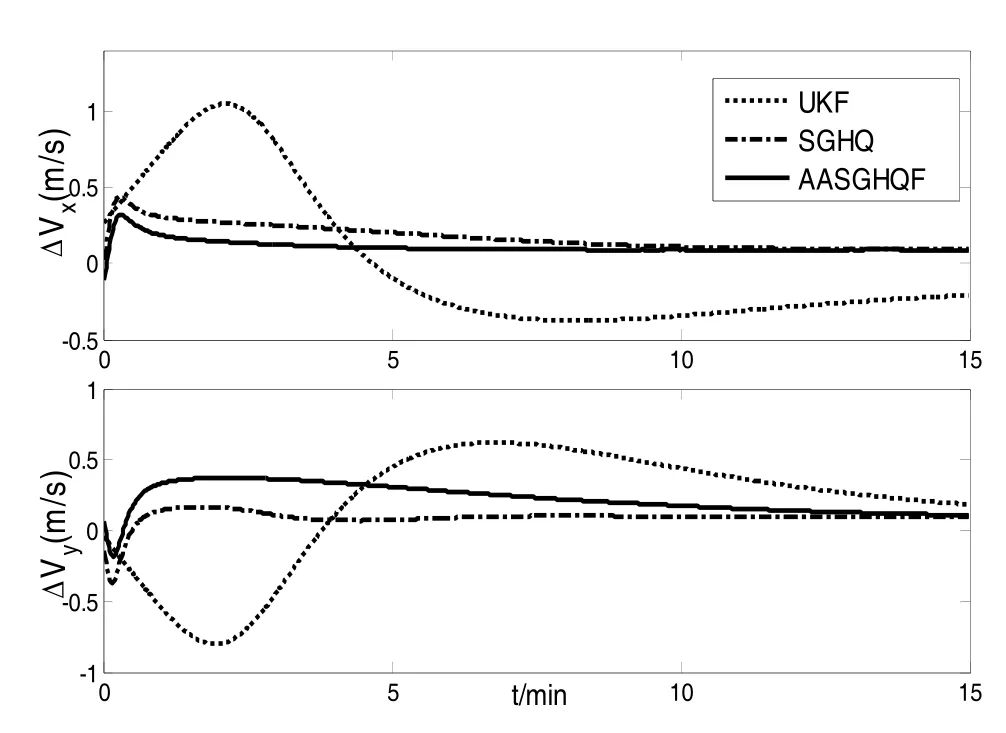
图4 速度估计误差Fig.4 Estimation error of velocity
4 结 论
本文建立了地理系下的舰机惯导传递对准非线性模型,提出了一种自适应各向异性稀疏高斯积分滤波算法,能够根据状态参数可观测度对各维变量分配积分点,摆脱了传统方法中均匀分配积分点的缺点。仿真对比分析表明,基于AASGHQF的传递对准方法具有较高的计算效率,可有效地提高舰机传递对准精度,满足舰载机惯导大姿态失准角下高精度初始对准的需求。
[1] 曲法义,魏纪林,崔乃刚,等. 机载精确制导武器快速传递对准[J]. 哈尔滨工业大学学报,2014,46(1):7-11.
QU Fa-yi, WEI Ji-lin, CUI Naigang, et al. Research on rapid transfer alignment for airborne precision guided weapons[J]. Journal of Harbin Institute of Technology, 2014, 46(1): 7-11.
[2] 梁浩,王丹丹,穆荣军. 基于状态参数可观测度分析的舰机传递对准自适应滤波方法[J]. 中国惯性技术学报,2014,22(1):58-62.
LIANG Hao, WANG Dan-dan, MU Rong-jun. Adaptive filtering algorithm based on observable degree analysis of state parameters in carrier-aircraft transfer alignment[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 58-62.
[3] 杨功流,王丽芬,袁二凯,等. 大方位失准角下舰载机快速传递对准技术[J]. 中国惯性技术学报,2014,22 (1):45-50.
YANG Gong-liu, WANG Li-fen, YUAN Er-kai, et al. Rapid transfer alignment of lager misalignment angle for carrier aircrafts[J]. Journal of Harbin Institute of Technology, 2014, 22(1): 45-50.
[4] Chattaraj S, Mukherjee A, Chaudhuri S K. Transfer alignment problem: Algorithms and design issues[J]. Gyroscopy and Navigation, 2013, 4(3): 130-146.
[5] Ding Zhijian, Cai Hong, Yang Huabo. Novel transfer alignment of shipborne gimbaled inertial navigation systems[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, 2014, 57(2): 93-100.
[6] Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE, 2004, 92(3): 401-422.
[7] Laura P, Pedro E. New state update equation for the unscented Kalman filter[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(5): 1500-1504.
[8] 巫春玲,韩崇昭. 平方根求积分卡尔曼滤波器[J]. 电子学报,2009,37(5):987-992.
WU Chun-ling, HAN Chong-zhao. Square-root quadrature Kalman filter[J]. Acta Electronica Sinica, 2009, 37(5): 987-992.
[9] Smolyak S A. Quadrature and interpolation formulas for tensor products of certain classes of functions[J]. Soviet Math, 1963, 4: 240-243.
[10] Jia Bin, Xin Ming, Cheng Yang. Sparse Gauss-Hermite quadrature filter with application to spacecraft attitude estimation[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 367-379.
[11] Nobile F, Tempone R, Webster C G. An anisotropic sparse grid stochastic collocation method for partial differential equations with random input data[J]. SIAM Journal on Numerical Analysis, 2008, 46(5): 2411-2442.
[12] Hermann R, Krener A J. Nonlinear controllability and observability[J]. IEEE Transactions on Automatic Control, 1977, 22(5): 728-740.
[13] 吴俊伟,孙国伟,张如,等. 基于SVD方法的INS传递对准的可观测性能分析[J]. 中国惯性技术学报,2005,13(6):26-30.
WU Jun-wei, SUN Guo-wei, ZHANG Ru, et al. Analysis on observability of INS transfer alignment based on SVD method[J]. Journal of Chinese Inertial Technology, 2005, 13(6): 26-30.
[14] 付梦印,郑辛,邓志红. 传递对准理论与应用[M]. 北京:科学出版社,2012:26-31.
FU Ming-yin, ZHENG Xin, DENG Zhi-hong. The theory and application of transfer alignment[M]. Beijing: Science Press, 2012: 26-31.
[15] Florian H, Viktor W. Estimation with numerical integration on sparse grids[J]. Discussion Papers in Economics, 2006, 4: 916-939.
Carrier-aircraft transfer alignment filter based on sparse Gauss-Hermite quadrature algorithm
LIANG Hao1, MU Rong-jun1, WANG Dan-dan2, CAI Ling3, QIAO Li-wei3
(1. Department of Astronautics, Harbin Institute of Technology, Harbin 150001, China; 2. Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China; 3. Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)
In view of the problems of large misalignment angles in carrier-aircraft INS’s transfer alignment, a sparse Gauss-Hermite quadrature filter(SGHQF) is applied to transfer alignment. To solve the problems of low utilization efficiency of points in SGHQF, a new adaptive anisotropic sparse Gauss-Hermite quadrature filter(AASGHQF) is proposed. The state parameters’ observable degree is quantized to classify the state parameters, and a mechanism for controlling the accuracy level of each dimension is presented by structuring adaptive anisotropic importance vector, in which the value of every element is determined according to grouped results. This mechanism can distribute the quadrature points nonuniformly and reasonably. Simulation results show that the AASGHQF algorithm has comparative performance with SGHQF and has a better performance compared with Unscented Kalman filter(UKF). The alignment precision of 3 arcmin could be improved to 2 arcmin by this algorithm. In addition, the number of AASGHQ points is decreased by 30%~60% and the computation efficiency is increased.
carrier aircraft; transfer alignment; nonlinear filters; observability; anisotropic; Gauss-Hermite
联 系 人:穆荣军(1969—),男,副教授,博士生导师。E-mail:murjun@163.com
1005-6734(2014)05-0587-06
10.13695/j.cnki.12-1222/o3.2014.05.006
V249.32
A
2014-05-26;
2014-09-16
海军重点预研项目(401010301);国防基础科研项目(C0320110001)
梁浩(1987—),男,博士研究生,研究方向为初始对准及信息融合。E-mail:liangwangyihao@163.com
