基于灰色理论的肥城盆地矿井涌水量预测

2014-10-23卜庆伟辛宏杰

山东水利 2014年6期

卜庆伟，辛宏杰，郭磊

（山东省水利科学研究院，山东济南 250014）

准确预测矿井涌水量的大小是制定最优排水方案，采用最优的防治水害措施，控制矿井水灾害事故发生和发展的关键。然而，矿井涌水量影响因素众多，预测难度较大。

目前矿井涌水量预测大体上可分为确定性分析方法和不确定性（随机）分析方法两类。相比于确定性分析方法，不确定性分析方法需要的基础资料相对较少，对矿井用水预测影响因素的处理方法相对简单。本文把灰色理论应用于肥城盆地矿井涌水量预测，有效解决了地质条件复杂、样本量小等问题，获得了较为理想的预测结果。

1 研究区概况

肥城盆地位于鲁中南山区，行政上大部分属于山东省肥城市，主要包括新城、老城、潮泉、仪阳、王瓜店、湖屯、石横、王庄、桃园等9个乡镇，面积约750 km2，人口约60万。盆地内工矿企业众多，是泰安市重要的工业基地。

近年来，随着经济的发展，水资源消耗量越来越大，而盆地内地表水缺乏，用水主要来自地下水，致使盆地内地下水水位大幅度下降。20世纪80年代以来，肥城盆地地下水水位每年下降1.9～2.4 m不等，这不仅给工农业生产、人民生活带来重大影响，而且某些煤矿区由于地下水位大幅度下降，加剧了采空区地面的严重变形塌陷，带来一系列环境问题。

与此同时，肥城盆地分布着106 km2的石炭——二迭系煤田，仅矿井排水多年平均就在4 000万m3左右，这些矿井水仅有10%得到灌溉利用，大部分排入康汇河，并与其他工农业生活污水混流，严重污染了当地环境。

2 灰色预测模型建立

灰色系统预测模型是一种全因果模型，其信息内涵丰富，可直接对输出序列建模，系统变量n取 1，为 GM（1，1）模型。建立 GM（1，1）模型只需一个数列，即 X（0）为原始数列：

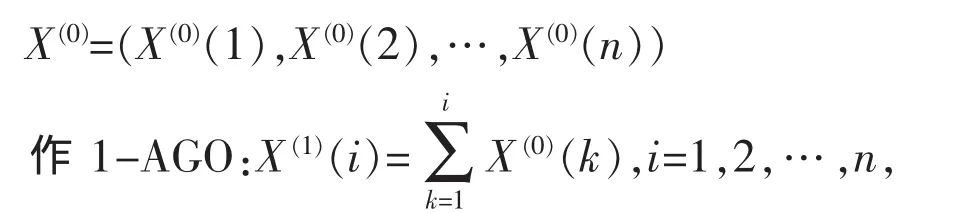
得到新数列：

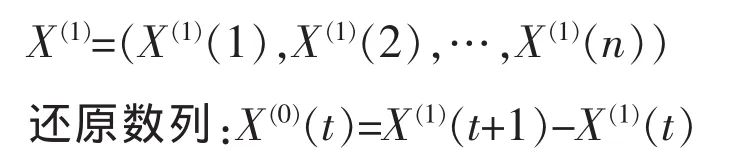
对于GM（1，1）得到的预测值是否可信，需要进行后验差检验。具体检验指标包括残差均值（ε）、后验差比值（C）、小误差概率（P）。根据经验，一般可按表1划分精度等级。

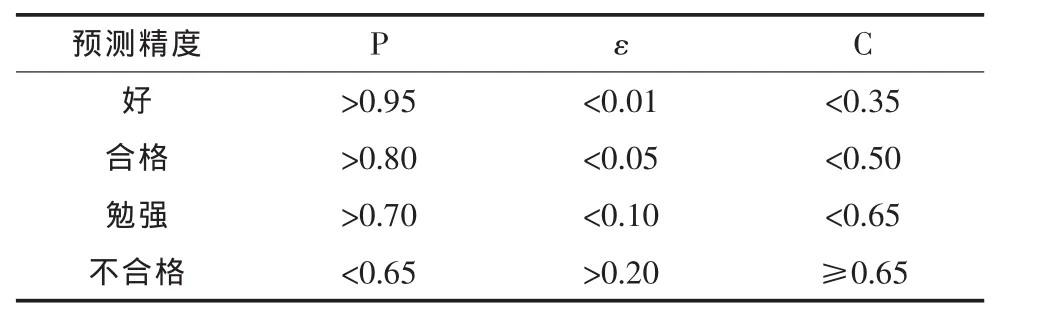
表1 精度判断表

3 矿井涌水量预测

肥城矿区的历年涌水量变化见图1：

图1 肥城盆地矿区历年矿井涌水量变化趋势图

从图1可以看出，1986年以来矿井排水基本稳定。然而，受到复杂水文、地质、气象、开采情况因素的影响，从上述曲线中很难发现明显的线性规律，如2003年的突变，资料显示，为国家庄煤矿8101工作面奥灰水突出导致该年份涌水量突然变大。

根据灰色预测原理，如果对原始数据经过一次1-AGO处理，则可以得到曲线见图2。原始数据处理后表现出很好的规律，这是因为利用灰色理论对原始数据进行处理后弱化了水文、地质、气象、开采情况因素对矿井涌水量的影响。

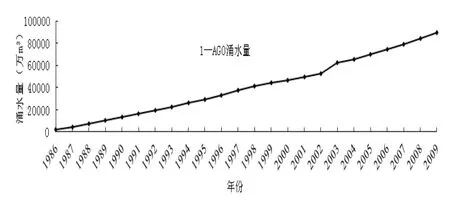
图2 1-AGO处理后肥城盆地矿区历年矿井涌水量变化趋势图

采用2004—2009年肥城矿区矿井涌水量数据，建立 GM（1，1）模型，通过计算机程序对数据进行拟合，得到的时间响应函数为：

累减得到还原函数为：

=3933.678exp0.06318k

（k=1，2……）

运用还原函数，分别模拟各年份的涌水量，对比模拟值与实际值的残差，判断该模型用于下一步预测的可行性，具体数据见表2：

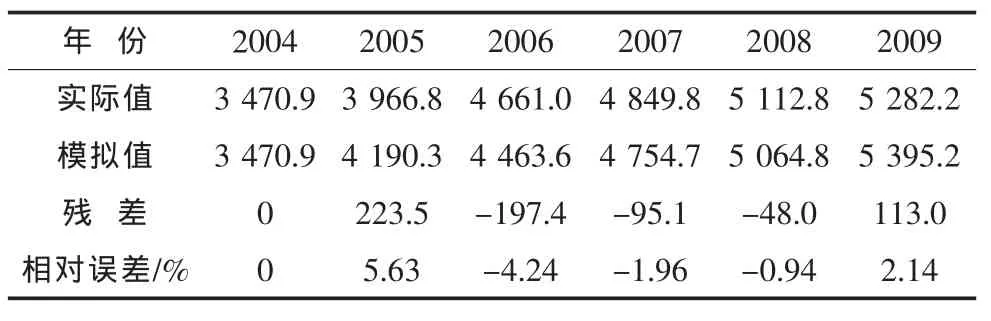
表2 GM（1,1）模型拟合肥城矿井涌水量结果表

由表2知，上述时间相应函数平均相对误差2.98%，通过后验差检验，该模型P=1，C=0.21<0.35，根据前面介绍模型精度评价指标，该模型为“好”，可以用作下一步的预测，由此函数进行的两步预测结果分别为：5 747.1、6 121.9。可以看出，未来肥城矿区的矿井涌水还会逐年增加，这对于今后矿井水资源利用工程设计及当地水资源供需分析提供了重要的数据支持。