对中国各行业年平均工资的函数性数据分析

孟银凤，梁吉业

（1.山西大学 计算机与信息技术学院，山西 太原 030006；2.山西大学 数学科学学院，山西 太原 030006）

0 引言

年平均工资（简记为平均工资）体现了企业的盈利程度及行业的发展程度，也反映了居民的收入水平。随着我国国民经济的飞速发展，各行业就业人员的平均工资都有所提高，与此同时，行业间的工资差距也呈现不断扩大的趋势。这已经引起了全社会的广泛关注，并对行业自身的发展、人们的择业观念、社会风气和社会稳定等方面都带来了不良影响。为了帮助政府在制定缩小收入差距的政策时提供一定的参考，本文搜集了中国2003到2011年间19个行业就业人员的平均工资［1］，并根据这些数据比较各行业的工资差距。其中这19个行业包括农林牧渔业（F1采矿业（F2制造业（F3电燃气水的供应业（F4建筑业（F5运输仓储和邮政业（F6）；计算机服务和软件业（F7）；批发和零售业（F8）；住宿和餐饮业（F9）；金融业（F10）；房地产业（F11）；租赁和商务服务业（F12）；科研和地质勘察业（F13）；水利环境公共设施业（F14）；服务业（F15）；教育（F16）；卫生和社会福利业（F17）；文化体育和娱乐业（F18）；公共管理和社会组织（F19）。

不同行业的平均工资均对应一个时间序列，因而从函数数据的角度去分析更加合理。就目前的研究文献来看，函数性数据分析方法的研究虽然在国外已经取得了丰硕的成果［2－5］，但总体来看还处于起步阶段，且很少用于经济数据的分析。国内在函数性数据方面的研究仅处于介绍和学习阶段［6－8］。不同于其他论文［5，8］，本文对平均工资这一函数数据分别运用函数性主成分分析和聚类分析两个方法研究它的行业分类状况。为此首先对数据进行了预处理，即将离散观测数据转化为函数数据，然后将处理后的函数数据用于主成分分析和聚类分析，其中聚类分析采用L2距离。

1 函数性数据的预处理

1.1 预处理的理论知识

对于一组二维数据，即平面上的n个点（xi，yi），i＝1，2，…n，诸xi互不相同。寻求一个函数（曲线）＾y＝f（x），使f（x）在某种准则下与所有数据点最为接近，即曲线拟合的最好。首先，确定所求曲线的形式（经验公式），而线性最小二乘法是解决曲线拟合最常用的方法之一［2，6］。令

其中：rk（x）是事先选定的一组基函数，ak是待定系数（k＝1，2，…，m，m＜n）。拟合的准则是使点（xi，yi），i＝1，2，…，n与其拟合值＾y＝f（xi）的距离δi的平方和（SSE）最小，称为最小二乘准则。进而得到关于a1，a2，…，am的线性方程组。其中

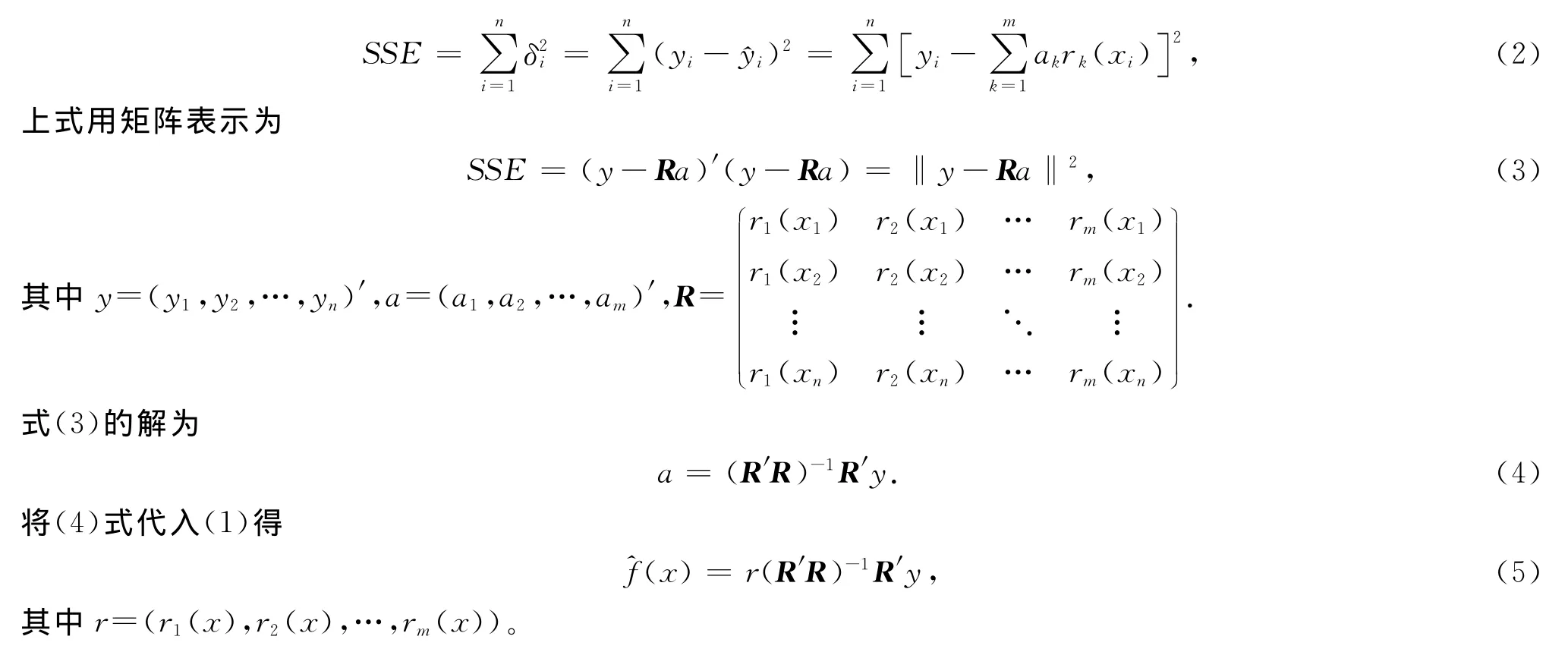
1.2 预处理的分析

这里我们采用多项式基对表1中的数据进行预处理，得到各行业就业人员平均工资的平滑曲线 及其速度变化曲线。

从图1可以看出：我国各行业就业人员平均工资在2003到2011年之间均呈现增长趋势，但增长速度各有不同。F7、F10、F13一直是各行业中的高薪产业，并且增长速度也快于其他产业。同时，金融行业在这几年间增长速度一直最快，使得它成为从2008年以后的“最高薪”行业。F2、F4、F6、F11、F12、F16、F17、F18、F19等几个行业的工资虽没有前面三个行业的工资那么高，增长速度也没那么快，但整体来说也一直是薪资不错的行业，这与国家的政策也一致，因为国家一直大力支持文教、卫生、社会福利业，以满足人民日益增长的精神需求。而在工资的比较中，F1、F3、F5、F8、F9、F14、F15等行业的工资属于薪资最低的，并且增长速度也是最慢的，这与我国属于劳动密集型的现状不无关系。

表1 中国2003年到2011年间19个行业就业人员的平均工资（元）Table 1 Average wage of employed persons in various industries in China from 2003 to 2011（yuan）

Fig.1 Smoothing curve and velocity curve of average wage for various industry employment图1 各行业就业人员的平均工资平滑曲线及速度曲线

Fig.2 Mean curve and standard deviation curve of average wage in various industries图2 各行业平均工资的均值曲线和标准差曲线

图2描述了我国各行业平均工资的均值曲线和标准差曲线。从均值曲线可以明显地看出我国各行业工资的平均变化趋势是逐年递增的，并且增长速度不断加快。由标准差曲线可以看出，各行业平均工资之间的差异随着时间的变化也越来越大。

2 函数性主成分分析及应用

2.1 主成分分析的理论知识

在函数性数据分析中，函数型变量记录了每一个观测对象的同一个变量某个区间上很多个时刻的数据信息，如果将时间看作与多元数据对应的变量（变化因素），则发现函数性数据分析面临着更大的“维度灾”。基于这种特点，可以将多元主成分分析技术引入到函数性数据分析中，称为函数性主成分分析［4－6］。其基本思想如下：

设xi（s）（s∈T），i＝1，2，…，N 为区间T 上的中心化后的平方可积函数，s对应多元主成分分析中的j，s是连续的而j是离散的。将区间T上的x（s）综合为一个变量

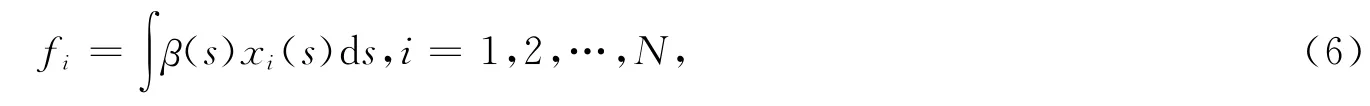
其中β（s）为加权系数，对应于多元主成分分析中的βj。第k主成分需满足下面的约束条件下的最大值问题［9］：

实践中，Var（fi）通常用样本方差取代 。记变量x（s）和x（t）的协方差为ν（s，t），有

求函数性主成分的权重函数β（s）的过程相当于解以下的特征方程［3－4］

其中λ为特征值。

函数性主成分的选择思想和多元主成分的相同［10－11］，也是确定累计贡献率。选择合适的K 使得达到所确定的累计贡献率，一般要求累计贡献率不小于85%。

2.2 函数性主成分分析的应用

基于Matlab软件，先将本文中拟合后的函数数据中心化，然后对中心化后的数据进行主成分分析，其前三个主成分的权重函数如图3。

第一主成分的贡献率是96.6%，即第一主成分能反映样本数据的96.6%的信息。同理，第二主成分的贡献率是3.2%，第一主成分和第二主成分的累计贡献率是99.8%。因此，前两个主成分能够反映样本数据信息的99.8%。所以可以将原来的高维数据降到2维。使用前两个主成分上的得分向量来代表样本数据，既能降维，又去除冗余信息。为了直观起见，给出各行业的散点图如图4。根据第一主成分的得分情况，可将各行业的平均工资水平大致分为三类（见图4）。

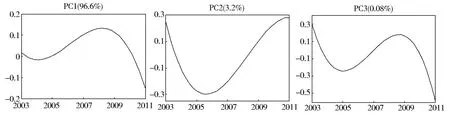
Fig.3 Weight function of different principal components图3 各主成分权重函数

Fig.4 Scattered point diagram of PC1 score and PC2 score图4 前两个主成分得分的散点图

3 函数性聚类分析及应用

3.1 聚类分析理论知识

在数据挖掘中，函数性数据聚类分析算法是一种常用的数据分析方法，它通过发掘函数性数据集中潜在的类结构，将分析对象分组成为由类似对象组成的多个类的过程，使类内的对象彼此相似，不同类的对象彼此相异。聚类问题的关键在于相似性测度方法。对曲线轨迹相似性测度的研究已有很多成果，主要可分为基于曲线数值模式和曲线形状模式的相似性测度［4，8，12］。使用聚类分析可以更好地研究数据信息，提取出对人们生活有利的信息。

在聚类算法中，对象与对象之间的距离的计算方法有很多种，本文中只利用L2距离：

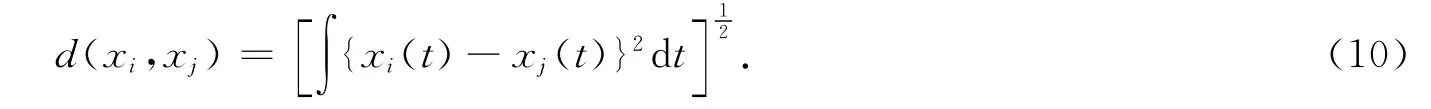
而类间距采用类平均法。

3.2 函数性聚类分析的应用

利用Matlab编写时间序列下各行业工资相似性的聚类分析程序，对构成我国19个不同行业就业人员平均工资及其增长速度的数据曲线进行聚类分析。聚类结果见图5和图6。图5的结构显示，可以将19个行业聚为平均工资收入明显不同的3类，各类行业平均工资曲线如图7所示。由图7可见：第1类属于薪资最高的一类，包括F7、F10、F13等3个行业。第2类属于薪资最低的一类，包括F1、F3、F5、F8、F9、F14、F15等7个行业。第3类的薪资居于前两类之间，包括F2、F4、F6、F11、F12、F16、F17、F18、F19等9个行业。事实上，这与主成分分析的结果一致（见图4）。

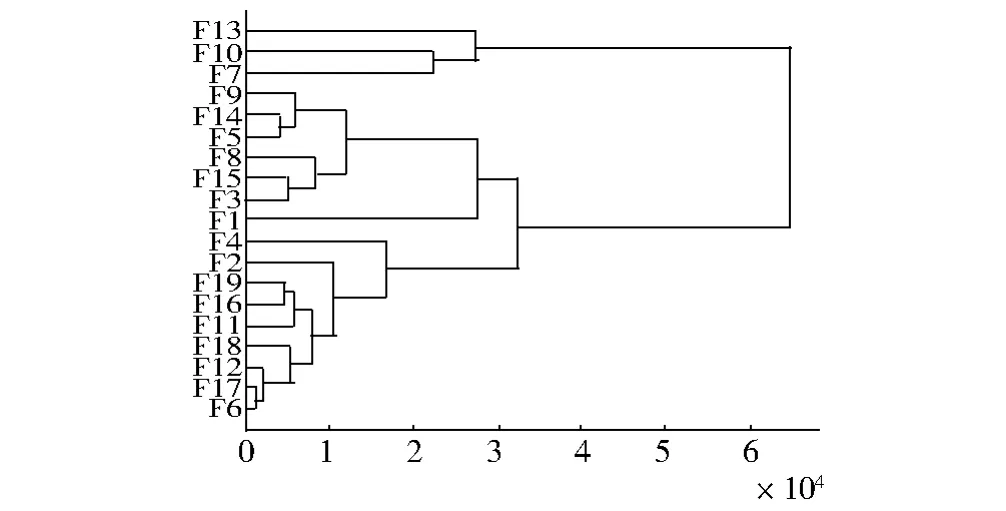
Fig.5 Average wage clustering diagram of 19 industries图5 19个行业平均工资的聚类图

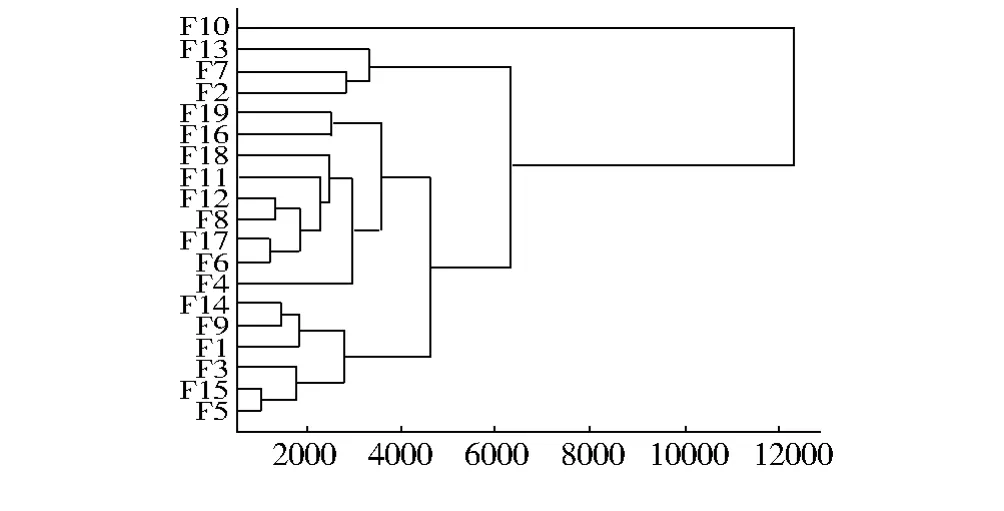
Fig.6 Average wage growth speed clustering diagram of 19 industries图6 19个行业的平均工资增长速度聚类图

实践中，对某些时间序列的分析而言，序列的速度变化趋势也是有用的深层次信息和研究的重要内容。因而我们对各行业的工资增长速度也进行了数据挖掘。根据图6，将速度曲线大致可以分为四类，见图8。第1类增长速度最快，包括F10。第2类速度次之，包括F2、F7、F13。第3类速度比第2类又稍缓，包括F4、F6F8F11F12F16F17F18F19等。第4类速度最缓，包括F1F3F5F9F14F15等。

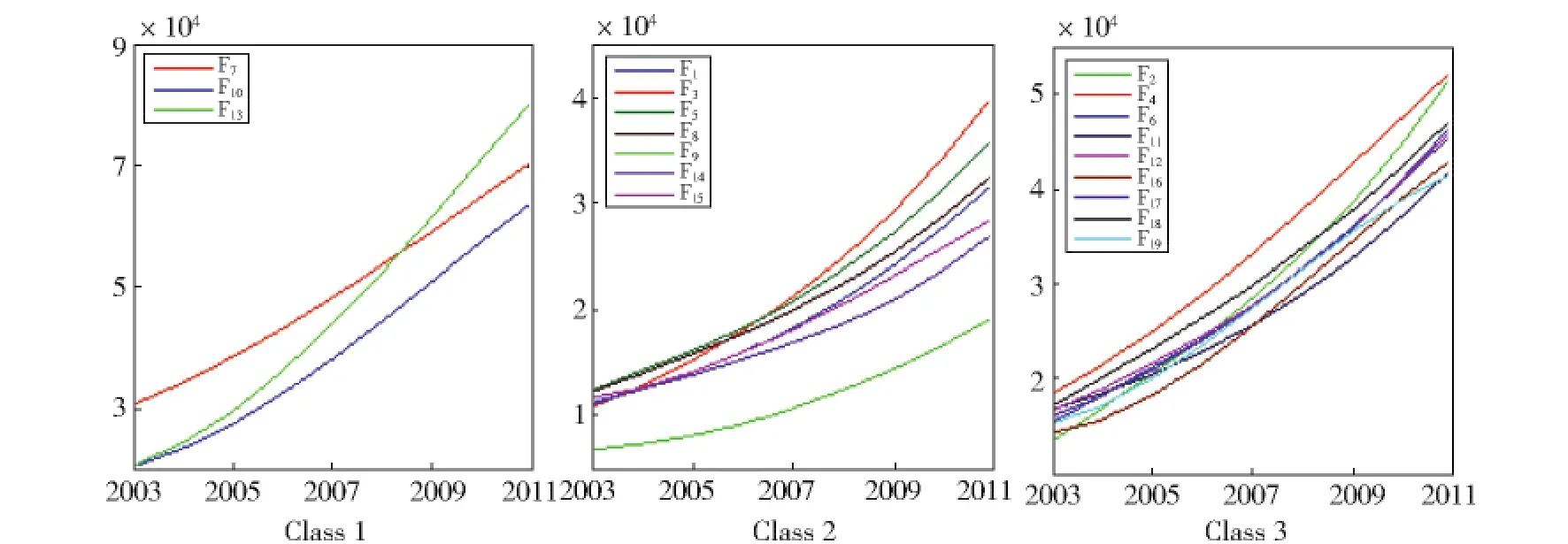
Fig.7 Classification diagram for average wage curves in different industries图7 不同行业平均工资曲线的分类图

Fig.8 Classification diagram for the growth speed curves of average wage in different industries图8 不同行业平均工资增长速度曲线的分类图

4 结论

本文运用两种函数性数据分析方法（函数性主成分分析和聚类分析）研究了我国各行业就业人员的平均工资数据。从聚类分析结果可知，我国科研和地质勘查业，金融业，计算机服务和软件业这3个行业属于高薪行业，并且增长速度相较于其他行业也是最快的；电燃气水的供应业，采矿业，公共管理和社会组织业，教育，房地产业，文化体育娱乐业，租赁和商务服务业，卫生社会福利业以及运输仓储邮政业这9个行业的工资次之；住宿餐饮业，水利环境公共设施业，建筑业，批发和零售业，服务业，制造业以及农林牧渔业7个行业属于工资最低一类，其增长速度相较于其他行业也比较慢。这与主成分分析的结果保持一致。说明我国目前各行业就业人员的平均工资基本呈现该特点。

［1］ 历年中国统计年鉴［Z］.北京：中国统计出版社，2012.

［2］ Cardot H，Ferraty F，Sarda P.Spline Estimators for the Functional Linear Model［J］.Statistica Sinica，2003，13：571-591.

［3］ Ramsay J O.When the Data Are Functions［J］.Psychometrika，1982，47（4）：379-396.

［4］ Ramsay J O，Silverman B W.Functional Data Analysis［M］.Second Edition.Springer，2005.

［5］ Lee H J.Functional data analysis：Classification and Regression［D］.Texas A ＆ M University，2004.

［6］ 严明义.函数性数据的统计分析：思想、方法和应用［J］.统计研究，2007，2：87-94.

［7］ 严明义.经济数据分析：一种基于数据的函数性视角的分析方法［J］.当代经济科学，2007b，1：108-113.

［8］ 靳刘蕊.函数性数据分析方法及应用研究［D］.厦门：厦门大学，2008.

［9］ 孟银凤，梁吉业，原曦曦.函数性数据分析中的主成分分析［J］.山西大学学报：自然科学版，2011，34（1）：21-25.

［10］ 朱建平.应用多元统计分析［M］.北京：科学出版社，2006.

［11］ 雷钦礼.经济管理多元统计分析［M］.北京：中国统计出版社，2002.

［12］ 朱建平，陈民恳.面板数据的聚类分析及其应用［J］.统计研究，2007，2：11-14.