生存曲线中Meta分析适宜数据的提取与转换

周支瑞，张天嵩，李博，毛智，曾宪涛，刘士新

生存分析（survive analysis）即是将终点事件的出现与否和出现终点事件所经历的时间结合起来的一种统计分析方法，生存分析得名于其通常研究的终点事件是死亡。当前，生存分析已广泛的运用于恶性肿瘤、慢性疾病或其他情况的随访研究中事件分析，比如疾病的发生、复发、伤口的愈合、某种症状的消失等。生存资料的分析主要特点就是考虑每个研究对象出现某一结局所经历的时间。生存曲线则是以生存时间为横轴，生存率为纵轴，将各个时间点对应的生存率连接在一起的曲线图[1]。

系统评价Meta分析中对生存资料的合并是一个棘手的问题，主要原因是较多原始研究无法直接获得效应量及其可信区间或原始数据。当前使用软件进行合并时，一般来说要获得以下三类数据：（1）O-E（logrank Observed minus Expected events）和V（logrank Variance）；（2）lnHR（风险比的对数）和SelnHR（风险比对数的标准误）；（3）lnHR（风险比的对数），lnLL（风险比可信区间下限的对数）和lnUL（风险比可信区间上限的的对数）[2,3]。这些类型的数据一般在原始研究中不会直接报告或仅报告了其中的某一部分，在这样的情况下就需要对数据进行正确的转换。然而，即便如此，有些数据还是无法获得，但多数的预后研究的文章会提供生存曲线，如何从生存曲线中获取有效的数据呢？本文将系统介绍如何从生存曲线中提取数据并进行合理的计算，最终获得可以用于合并的数据[4-6]。

1 生存资料Meta分析的方法

当前，制作生存资料Meta分析的方法有以下几种方法[2,7-10]：

第一，通过非编程软件完成。当前可用的有Review Manager 5（RevMan 5）和Comprehensive Meta Analysis V2（CMA V2）。一般来说要直接获得或通过数据转化获得以下三类数据才能进行有效合并：（1）O-E和V；（2）lnHR和SelnHR；（3）lnHR，lnLL和lnUL。

第二，通过编程软件完成。如Stata、R、JAGS、BUGS、Stan软件。一般来说要获得以下两类数据才能进行有效合并：（1）lnHR和SelnHR；（2）lnHR，lnLL和lnUL。

第三，在HR无法计算的条件下，也可选择相对危险度（RR）或者比值比（OR）为效应量。这种方法存在一些固有的缺陷，主要因为HR考虑了发生终点的时间所经历的时间，但RR或者OR并未考虑时间因素，较HR丢失了一些重要的信息，故采用RR或者OR作为生存资料的效应量不作为常规选择。这种方法与常规的二分类数据的Meta分析是一样的。

第四，IPD的Meta分析。因该类Meta分析数据难以获取且国内开展的可能性极小，故不作展开介绍。

2 生存曲线图的获取及处理

以下将以实例的形式演示如何从生存曲线中提取Meta分析所需要的各时间段的生存率并通过计算获得Meta分析所需要的数据。

2.1软件的下载与安装本文主要应用的软件为图形数据提取软件Engauge Digitizer 4.1，软件下载地址为：http://sourceforge.net/projects/digitizer/。此类软件有很多种，本文仅介绍Engauge Digitizer，因为该软件相对简单并且容易获得，而且完全免费。下载软件并解压后双击Engauge.exe即可使用，可创建桌面快捷方式方便下一步操作。

2.2图片获取从原始文献中获取的图片要足够清晰，建议至少到达300dpi，原始文献尽可能选择下载高质量的PDF格式。本文示例为《lancet oncology》上的一篇Ⅲ期随机对照试验《Continuation of bevacizumab after first progression in metastatic colorectal cancer （ML18147）：a randomised phase 3 trial》[11]。获得PDF格式的全文以后，再通过Windows操作系统自带的截图工具截取该图片。

具体操作方法为：尽可能放大使图在屏幕上完全显示，并且包含完整纵横坐标，点击键盘右上角的“PrtScn”键，再按照“所有程序→附件→截图工具”打开画图工具并使用“Ctrl+V”将图片黏贴到画图工具中，再存为JPG格式并重新命名。

2.3图片处理由于Engauge Digitizer 4.1软件仅能识别灰度图，对于生存曲线为彩色线条的图片需要常规将其调整为黑白图片。此时可以借助于很多图片处理软件实现，最常用的就是Adobe Photoshop。将截图并保存的图片导入Adobe Photoshop CS5软件进行去色，去色的方法为依次点击“图像→调整→去色”即可实现。去色后，还需通过色阶功能使黑白对比明显，操作方法为通过“图像→调整→色阶”调出对话框，详见图1。处理后的图片如图2所示。

3 连续取点法提取生存曲线数据

3.1图片导入把处理后的图（图2）导入Engauge Digitizer 4.1软件，导入方法及导入后状态如图3所示。

3.2新建曲线并命名因为本例坐标中有2条生存曲线，故需要新建2条待提取数据的曲线。根据原文，将两条曲线分别命名为“chemotherapy”和“b e v a c i”。如图4所示，依次点击“Settings →Curves →New”。新建曲线可点击“properties”设置线型和颜色，有助于取点时区别两条生存曲线。

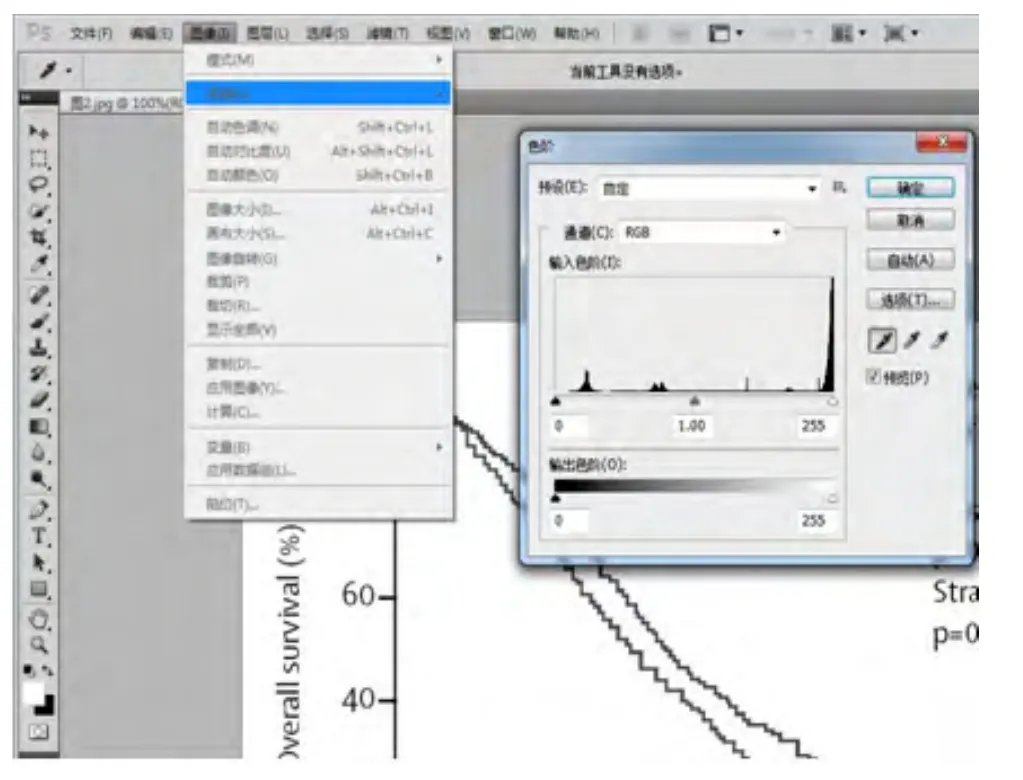
图1 通过色阶功能处理图

图2 通过去色及色阶处理后的图片

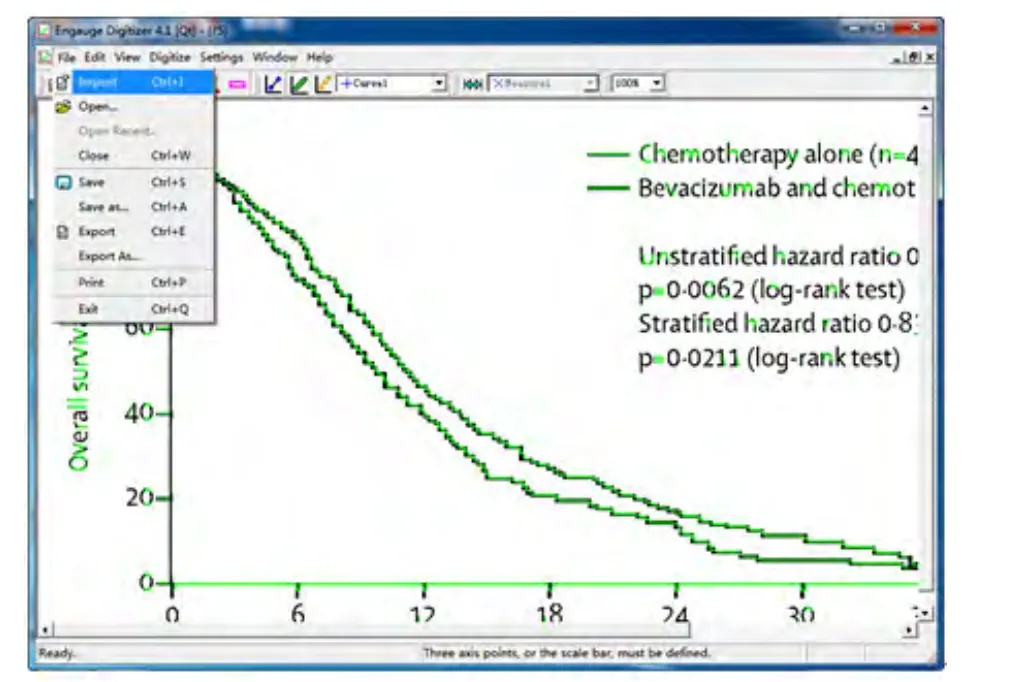
图3 将图片导入Engauge Digitizer 4.1软件

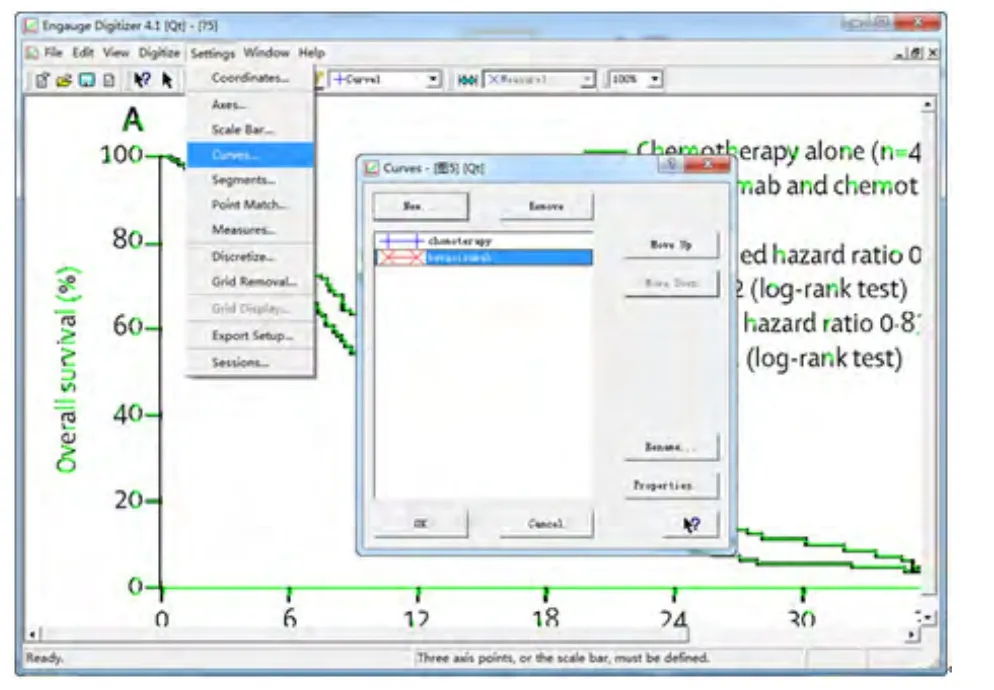
图4 新建及命名生存曲线的方法

3.3确定原点及纵横坐标轴的刻度一般首先确定原点，然后分别确定X轴与Y轴的刻度，此步骤其实是在原图的基础上重新构建一个二维坐标系，在这个新建的二维坐标系中的任何一个点都可以通过（x,y）表示。依次点击“Digitize →Axis Point”，调出图5所示对话框并行相关设置。

3.4分别对两条曲线进行连续取点选择连续取点工具分别对“chemotherapy”及“bevaci”两条曲线进行连续取点，此工具把鼠标移动到相应的位置可自动识别取点的区域，但需要注意同一个坐标轴中有2条曲线时需要按照原图进行分辨，尤其是当两条曲线非常接近之时，不能把一条曲线上的点误认为是另外一条曲线的点。取点方法如图6所示。

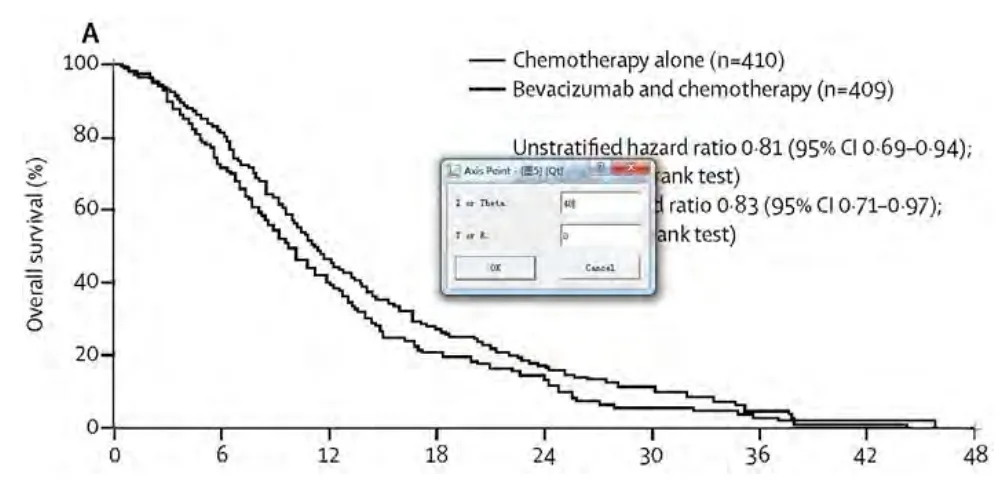
图5 确定原点及纵横坐标轴的刻度的方法

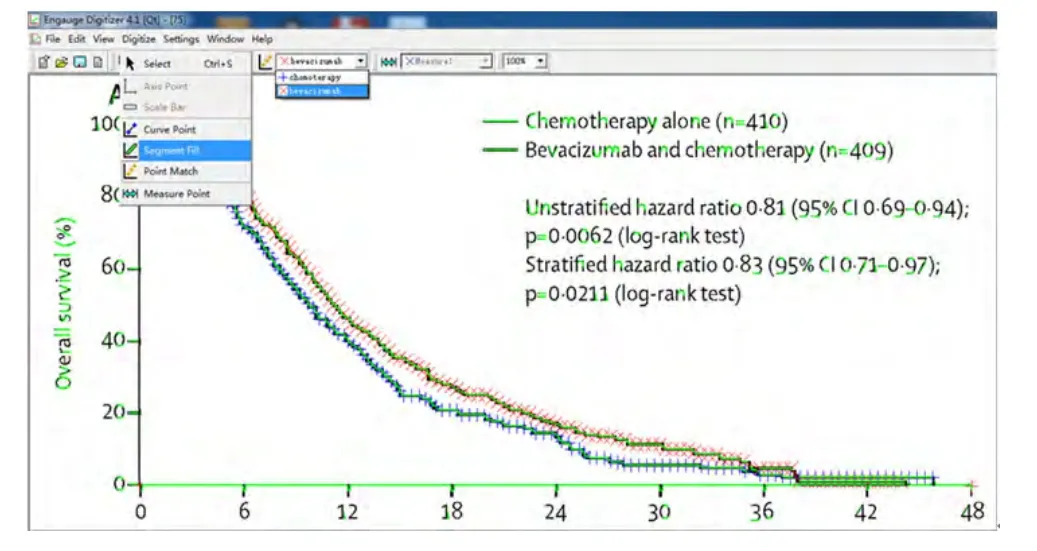
图6 使用连续取点工具分别对两条曲线连续取点

3.5导出并存储生存率数据软件默认的导出数据的文件格式为“.csv”，这也是通用的数据存储格式，可通过Excel软件打开。本例选择存贮于桌面，方法为依次点击“File →Export”，在弹出的对话框中选择桌面进行命名（本文命名为“图5.csv”）后，点击“保存”即可。

3.6筛选生存率数据由于采用的是连续取点法提取数据，故密集的取了很多点，得到了很多数据。然而，实际操作中并不需要如此多的数据用于后续的计算，故还需对提取的数据进行初步的筛选。

首先通过Excel打开“图5.csv”文件，然后把X这一列设置小数位数为0位，其余两列数据小数位数设置为2位，如图7所示。然后，选取时间点为0、3、6、9、12、15、18、21、24、27、30、33、36、39、42、45月时对应的生存率数据，并删除不需要的数据。

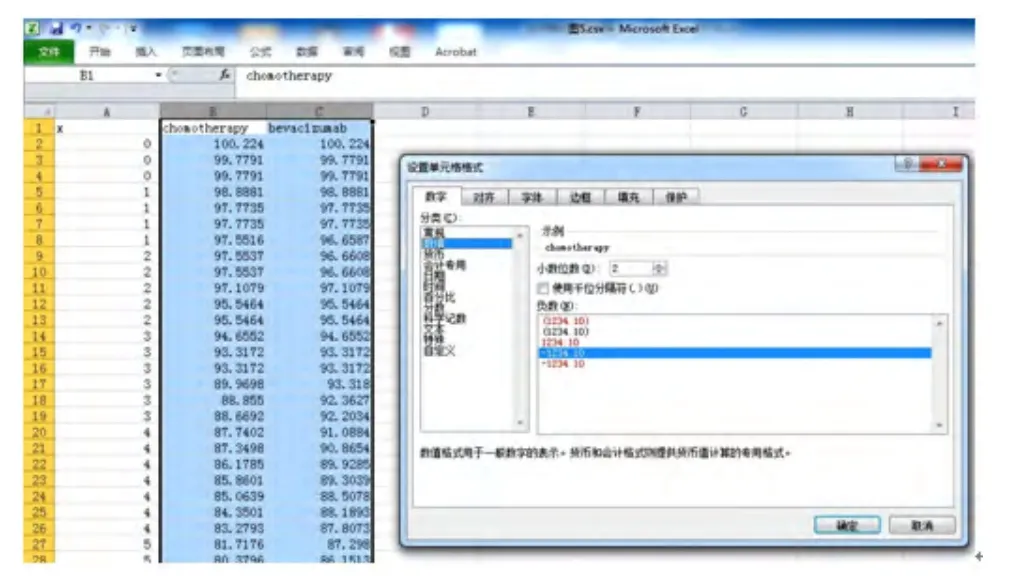
图7 导出的数据及设置各列小数位数的方法

需要说明一点：一般后一个时间点的生存率不可能大于前一个时间点，但因数据提取时存在误差，可能出现后时间点生存率略大于前时间点，且这种情况多出现于生存曲线是水平线时，故需要对数据进行合理的整理。如果出现后一个时间点生存率的数据大于前一个时间点的情况，需要把后一个时间点的数据用前一个时间点的生存率数据代替，理由是前后时间点生存率相等是符合客观情况的。此外还要注意，在随访开始时，一般0时间点的生存率为100%。处理后的数据如图8所示。

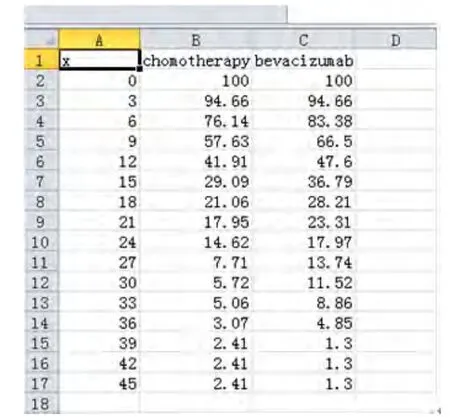
图8 最终用于生存率计算的数据

4 计算lnHR和SelnHR

lnHR和SelnHR计算的具体方法可参考Jayne F Tierney等人的文献[5]。实际上并不需要根据这些原始数据去直接计算Meta合并需要的数据，Jayne F Tierney等人的文献提供了计算lnHR和SelnHR的excel程序文件，使用者只需要按要求填入相应的数据及对应的信息即可，该程序文件下载地址为http://www.biomedcentral.com/content/supplementary/1745-6215-8-16-S1.xls。

这个Excel计算程序共计7个工作表，每个工作表都有特定的作用，本文主要就其中的与生存曲线数据提取相关的工作表作简单介绍，其他计算方法读者可参考Jayne F Tierney等人的文献。

4.1命名各研究组的名称在工作表（1）中输入本例中研究组的名称，在Research一栏中输入“bevacizumab”，在Control一栏中输入“chemotherapy”，如图9所示。提示一点：此步骤不是必须的，之所以需要命名是为了便于后续操作，具体的命名要根据实际情况确定。

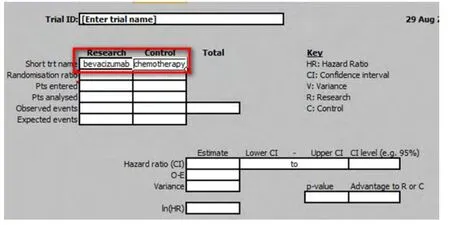
图9 命名各处理组的方法

4.2输入数据在工作表（2a）中follow-up一栏中填入随访时间（一般输入随访时间的范围，本例中原文并没有直接提供随访时间范围，仅报告了随访时间的四分位数间距，笔者通过合理的估算填入了5～45.1月），此处必填，主要用于估计截尾数据。接着，依次输入随访时间点，各时间点各组的生存率及各组的样本例数（此处样本例数应该填入进入ITT分析的样本例数）。在本步骤填写过程中如果出现红色字体提示，那就表示填写或者计算过程有错误，需要重新核对错误的原因。整个填写过程如图10所示。

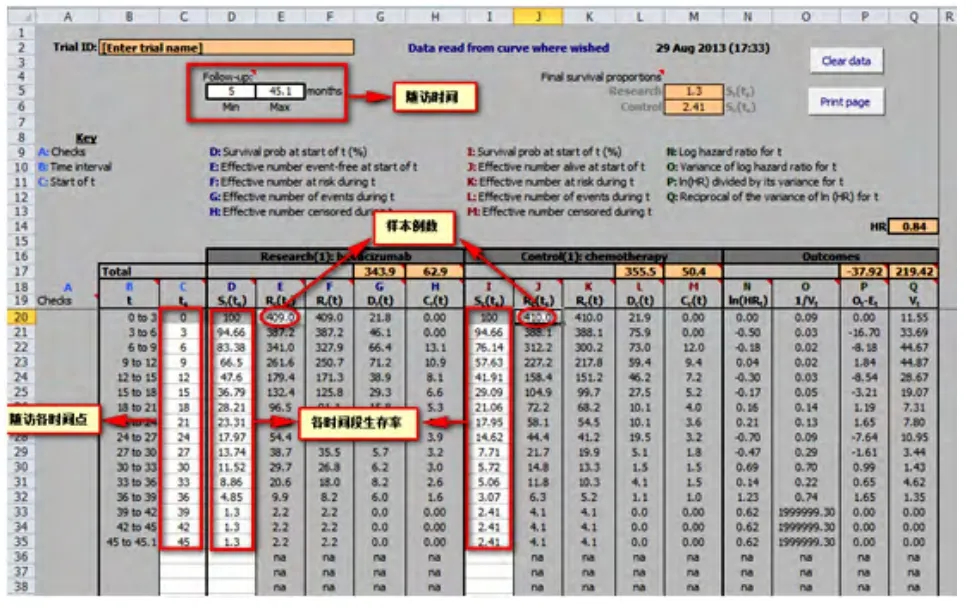
图10 填入对应的信息及数据

4.3模拟生存曲线工作表（2a）填写完毕后，在工作表（2b）中即可自动显示按照提取的生存曲线数据重新模拟的生存曲线。可在此与原文中的生存曲线进行比较，判断是否有大的差别，如果有很大的差异需要重新寻找原因。本例中模拟的生存曲线与原文生存曲线相似，如图11所示。

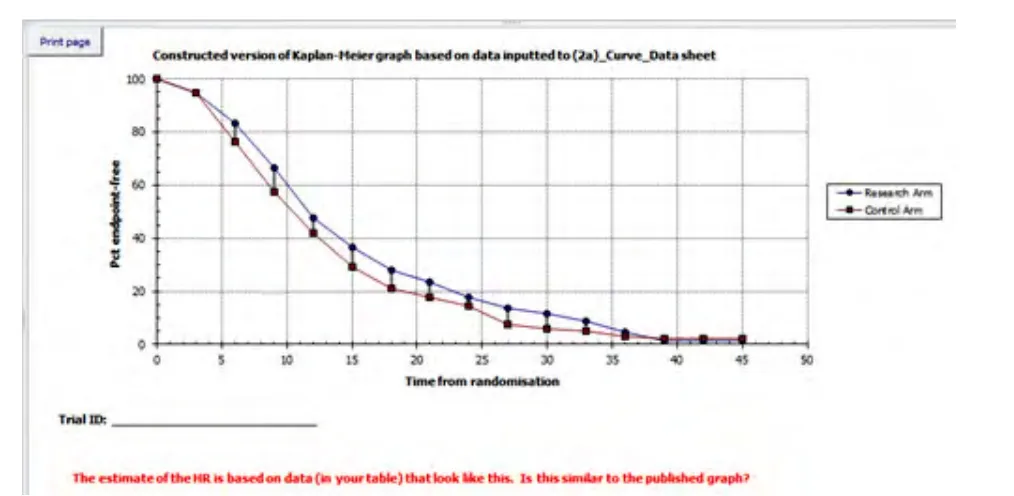
图11 模拟的生存曲线

图12 计算结果展示

4.4展示结果工作表（4）中展示了估算的结果，包括了进行Meta合并的所有必须数据，如图12所示。本例中估算的HR及95%可信区间为：HR=0.84，95%CI：0.74～0.96；原文中报道的HR及95%可信区间为：HR=0.81，95%CI：0.69～0.94。可以看出，估算的结果与原文计算的结果很接近。

5 间断取点法提取生存曲线数据

上述介绍了连续取点法提取的过程。如果仅需要从生存曲线选取所需要的点进行数据提取，并不希望像连续取点法那样先取数个点再进行筛选和删除，就可以选择间断取点的方法进行数据提取。为了便于比较，仍选取时间点为0、3、6、9、12、15、18、21、24、27、30、33、36、39、42、45月时对应的生存率数据进行提取。

首先，借助Adobe Photoshop划分图片确定生存曲线上目标时间点对应的生存率所代表的点。将图导入Photoshop后，选择切片工具，并通过拖拉参考线把整个坐标区域框定，如图13所示。

第二步，平均划分坐标区域为16等分（因本例按每隔3个月取一个点，故平均划分为16等分，其他的实例需视具体情况而定），如图14所示。

第三步，选择直线工具并按照上一步骤事先划分的标记画垂直竖线，垂直竖线与生存曲线的交点即是需要提取数据的点。至此我完成了已知横纵坐标的数据点，如图15和图16所示。完成后进行保存备用。

最后一步，将保存好的图16导入Engauge Digitizer 4.1软件，新建Curves、确定坐标轴的原点与纵横坐标的刻度、后续取完点之后的计算等操作步骤与连续取点法相同；唯一不同点是取点时需要选择间断取点工具，如图17所示。

6 结语

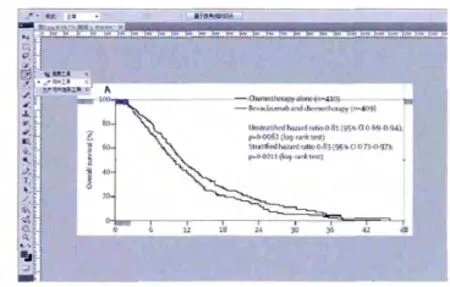
图13 选择切片工具框定坐标区域

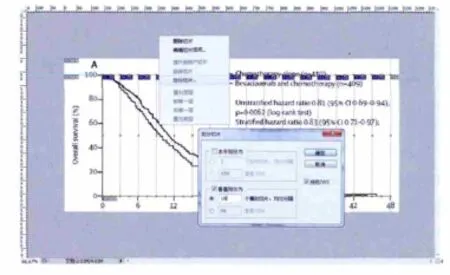
图14 平均划分坐标区域的方法

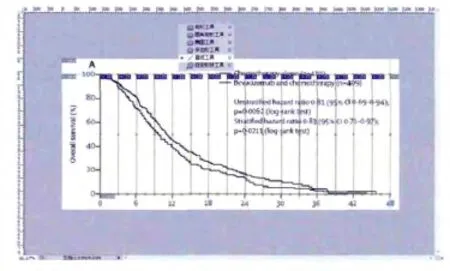
图15 使用直线工具画垂直竖线

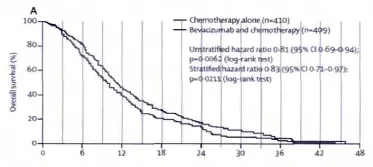
图16 可用于间断取点法提取数据的生存曲线

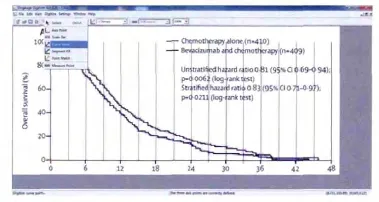
图17 间断取点法在生存曲线上取点

目前从曲线或者图形中提取数据的软件很多，曲线是一种二维图形，该类型的数据提取是相对较简单的一种，各种数据提取软件的原理大致相同，一般是按照原图确定原点及纵横坐标轴以重建一个二维坐标系，然后通过重建的二维坐标系确定其中任意一点的坐标。数据提取本身并不难，由生存率数据计算Meta合并所需要的中间数据我们可根据Jayne F Tierney等人[5]共享的Excel程序进行计算，过程也并不难。但是以上操作是基于对生存分析深刻理解上的，所以建议读者能系统学习生存分析的理论及概念。

本例中间断取点似乎并没有显示更多的优越性。主要原因在于对于生存曲线需要取多个点，有些图形的数据提取并不需要提取太多的点（比如仅需要几个点），这种情况下间断取点似乎更有优势。无论采用何种取点方法，具体建议读者根据目标数据的特点、结合文章的背景而定。

[1]孙振球,徐勇勇. 医学统计学[M]. 北京:人民卫生出版社,2010:299-325.

[2]Higgins JPT,Green S. Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0 [updated March 2011]. The Cochrane Collaboration, 2011. Available from www.cochrane-handbook.org.

[3]Sterne JAC. Meta-Analysis in Stata: An Updated Collection from the Stata Journal [M]. Stata press,2009.

[4]Guyot P,Ades AE,Ouwens MJ,et al. Enhanced secondary analysis of survival data: reconstructing the data from published Kaplan-Meier survival curves[J]. BMC Med Res Methodol,2012,12:9.

[5]Tierney JF,Stewart LA,Ghersi D,et al. Practical methods for incorporating summary time-to-event data into meta-analysis[J].Trials,2007,8:16.

[6]Williamson PR,Smith CT,Hutton JL,et al. Aggregate data meta-analysis with time-to-event outcomes[J]. Stat Med,2002,21(22):3337-51.

[7]曾宪涛,Joey S.W. Kwong,田国祥,等. Meta分析系列之二: Meta分析的软件[J]. 中国循证心血管医学杂志,2012,4(2):89-91.

[8]董圣杰,冷卫东,田家祥,等. Meta分析系列之五: 贝叶斯Meta分析与WinBUGS软件[J]. 中国循证心血管医学杂志,2012,4(5):395-8.

[9]曾宪涛,田国祥,张超,等. Meta分析系列之十五: Meta分析的进展与思考[J]. 中国循证心血管医学杂志,2013,5(6):561-3.

[10]罗杰,冷卫东. 系统评价Meta分析理论与实践[M]. 北京:军事医学科学出版社, 2013.

[11]Bennouna J,Sastre J,Arnold D,et al. Continuation of bevacizumab after first progression in metastatic colorectal cancer (ML18147): a randomised phase 3 trial[J]. Lancet Oncol,2013,14(1):29-37.