基于quartus II的计算机运算器设计
2014-10-21田小敏
田小敏
【摘 要】随着EDA技术、CPLD/FPGA的迅猛发展以及相关软件的日益成熟,利用计算机来设计计算机成为一种行之有效且势在必行的新方式。本文基于Q uartus II 6.0的图形设计方式,辅助Verilog HDL语言,以封装的基本逻辑单元为基础设计了4位定点除法器。仿真结果表明,本文设计的除法器能够完成预期的除法运算功能。
【关键词】Q uartus; II 6.0;除法器设计;CPLD/FPGA
1 手工除法运算方法分析
计算机内部数据一般用补码表示[1],为了找出适合于计算机运算器执行的除法运算方法,下面以4位二进制数为例分析手工除法算法[2]。
正整数做除法运算时,商的数码由高到低生成,确定商之前需要比较被除数与除数位数相同的部分是否够减,不够减商位0,够减商为1[3]。由于这种试商操作是从被除数的高位开始的,为了保证位数的一致性,将被除数的最高位填写3个”0”,然后进行4位数的比较。每次得到的部分差要左移一位,最低位要由被除数没参加比较的下一位填充。当被除数的最低位数码经过试商,前次部分差和此次一位商与除数的积相减后,得到的部分差就是余数。
分析该手工除法运算方法可知:当部分积为0时,要直接将前次部分差左移一位,使之低3位的成为下一次的被减数的高3位,否则,将本次减法运算的结果左移一位,使之成为被减数的高3位。
整个除法的运算过程认定除数是不动的,那么被除数和商是每步相减之后,到要左移一位,添加下面一位,然后与一位乘积做减法。
2 正整数除法器设计
按照上述分析在Quartus II[4]中设计正整数除法电路如图1所示。主要部件为加减运算单元,保存为cfq1.bdf。用一条输入线和它的非门的或运算给减法控制线sub赋值1。正整数除法的除数和被除数的最高位均为0,因此,将补充的被除数的高3位直接同被除数的最高位连在一起,就能够得到使高位补充数码都为0的目的。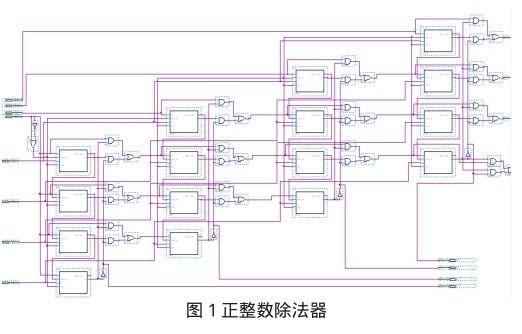
每次试商的时候要判断部分差是否够减,判断的过程就用减法器来进行。当减法器输出的最高位是1时,表明试商时不够减,因此本位商的数码应是0,否则是1。
本次试商的数码可以直接用非门电路从减法运算的最高位得到,部分差可以又能够减法器的最高位控制。当本次减法输出的最高位是1时,就表示不够减,因此要让上一次的部分差做下一次的被减数;如果够减,就让本次减法运算的差做下一次的被减数,这种设计被称作本位差逻辑。除数被送到每次减法运算的b输入端,被减数是通过本位差逻辑送到被减数a端的,通过商数码线就得到本位商。当被除数的最低位试商过后,本位差逻辑的输出就是除法的余数。
3 正负对称区间除法器设计
正负对称区间上有符号除法器是在正整数除法器基础上设计的,首先将有符号数转化成绝对值,然后利用正数除法器计算,最后将结果利用符号关系进行转化。
3. 1 结果转换控制电路设计
结果转换控制电路时根据求补码的方法进行的[5]。转换编码是根据有符号数的最高位来求补码的,从而达到求商或余数符号的目的。根据除法运算的符号规定,通过输入数的最高位同号还是异号来决定商的符号。当除数和被除数符号相反时,用它们的异或表示,并用这个标志线来将商改成附属的补码表示形式。余数的符号就是由被除数符号来确定。
3. 2 对称除法器设计
对称除法器的电路如图2所示。在正数除法器前端输入初添加绝对值电路,后端添加转换控制电路。
4 实用除法器设计
实用除法器前端要设计除数为0的控制,还要设置最高位是1且其余各位都是0的最小負数的判断,它是限位计数表示的最小数,也是补码制的最小的数。如果除数为0,那么应立即中止除法计算,并报警。如果遇到除数是最小数但被除数不是最小数的情况,那么商就是0,余数是被除数。如果除数被除数都是最小数,那么商就是1,余数是0,如果只被除数是最小数的情况,那么可以用绝对值比它小1的数代替做除法,然后调整余数和商,最后能得到正确结果。调整余数和商的方法是将余数的绝对值加1,然后与除数比较,若等于除数则商加1余数为0,不然只是将加1的结果作余数。
4.1 最小数判断电路
当标志线为0时,表示否定;标志线为1时,表示肯定。电路图如3所示。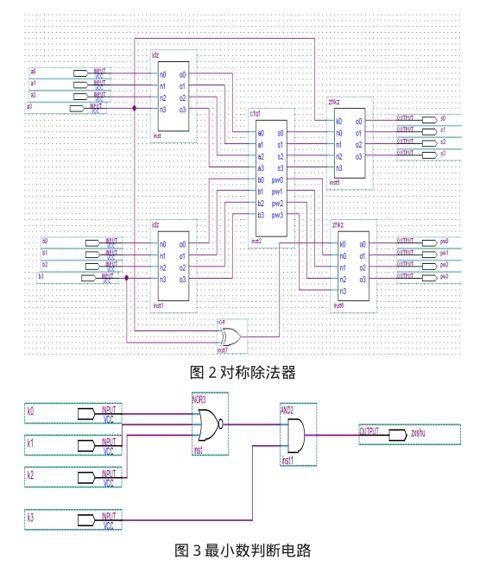
4. 2 仅除数是最小数的判断
利用对称区间的有符号数除法器进行除法运算的关键是变为绝对值进行,因而当除数是最小数时,它的绝对值最大,任何相同位数的数的绝对值都不会超过它,这样商是0,余数是被除数。表明仅除数是最小数的因素有两条线,一是数据a的最小标志线,二是数据b的最小标志线,确定仅除数是最小数的应是它们的联合。当仅除数最小标志线为1时,通过一个非门将前面运算的结果都归0了,因此商是0。另一方面,由仅除数最小标志线直接控制余数,和被除数通过与门和或门输出余数。
4. 3 除数与被除数都是最小数的设计
除数与被除数都是最小数的除法相对简单,只要商1,余数为0即可。a,b最小线同时为1的标志线,通过非门控制运算输出。控制余数的与门组使余数为0,而商的控制有了变化,这时仅使商的高位全为0,而最低位通过特殊设计使之为1,从而使商位1。
4. 4 被除数是最小数的设计
实用除法器最为复杂的设计应属被除数是最小数的设计了。解决这一问题的办法是求最小数相邻的数与该除数的除法运算结果,然后判断余数加1是否等于除数,如果等于,则商加1,余数为0,否则用加1后的数做最终的余数。具体分以下几步:
(1)求最小数的相邻数
经分析知道,最小数最高位是1,其余都是0,将这个数加1的结果是只有最低位变成了反码,所以对被除数最低位加异或门。
(2)加1电路设计
将减法器的b输入端和加减控制端都置为0,为了能够控制是否加1,又在最低的进位端引进了被除数是最小数而除数不是的标志线f,当f = 1时,输出数据就是输入数据加1,否则不进行加1运算。
(3)判断余数加1是否与除数相等
用最小数相邻数做除法,得到的余数必须加1,但加1之后的值有可能等于余数。如果相等,商必须加1,以0作为余数;如果不等,那么加1之后才是所求余数。当相减 结果是0时,由f和zfh与运算的非决定着是否输出非0余数或余数0。f=1表示被除数是最小数,除数不是。zfh=1表示加1后的余数与除数相等,否则不等。因此f和zfh的与运算的非能够决定输出的余数。
(4)求最后的商
商的最终结果取决于余数的计算,是否加1要由标志线zfh控制,当zfh=1时商加1,否则不加。
5 除法器总体设计
实用4位除法器的完整电路如图4所示。要说完整,还要添加除数为0的判断,建立中断,本文暂不考虑。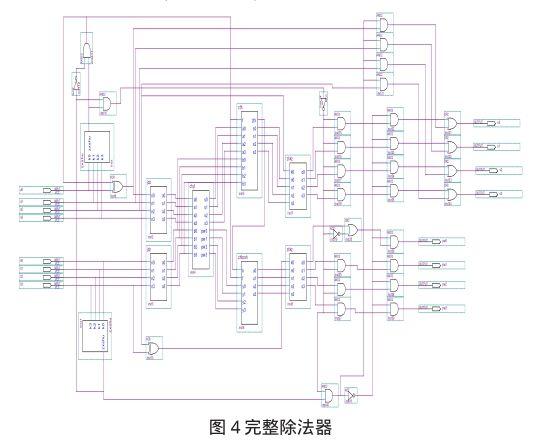
仿真结果如图5所示。计算1000除以0011,被除数为最小数,商为1110,余数为1110。其它三种情况也都仿真成功,说明除法器设计成功。
6 小结
本文基于QuartusII平台设计了4位除法器,仿真结果表明,该除法器能够完成4位带符号数的除法操作。该除法器的运算位数可以根据需要增加,只是电路设计更加复杂,但原理相似。在本文設计的除法器基础上进一步加上存储器,控制器,接口,中断,DMA,输入输出设备等,成为一个比较完整的8位除法计算器。
参考文献:
[1]余孟尝.数字电子技术基础简明教程[M].北京:高等教育出版社,1999:5- 65.
[2]姜咏江.基于QuartusII的计算机核心设计[M].北京:清华大学出版社, 2007: 50- 75.
[3]蒋本珊.计算机组成原理[M].北京:清华大学出版社,2002:43- 48.
[4]潘松,黄继业.EDA技术实用教程[M].北京:科学出版社,2006:127- 190.
[5]赵保经.中国集成电路大全TTL集成电路分册、COMS集成电路分册[M].北京:国防工业出版社,1985:23- 28.
