地震作用下岩质边坡动力响应分析

2014-10-21何江达谢红强肖明砾

水力发电 2014年2期

李鹏，何江达，谢红强，肖明砾

（四川大学水利水电学院，四川成都 610065）

我国西部是一个多山多地震的地区，由地震造成的边坡失稳案例不计其数，强地震作用下水电站边坡的动力响应是工程界普遍关心的问题。目前，边坡动力分析方法主要有拟静力法、滑块分析法以及数值分析法。拟静力法因其方法简单实用从而在工程边坡动力分析中广泛应用，但不能反应震动次数、频率以及持续时间，也没有考虑材料阻尼等性质，故不能反应地震的时程特性；滑块分析法基于刚体模型假定，通过假定滑动面确定屈服加速度值，并将其与等效加速度对比，从而确定滑动面在地震过程中产生的残留位移，当残留位移大于容许位移，则判定为不稳定，否则为稳定；数值分析方法中最主要的方法是有限单元法，动力有限元法不仅考虑了荷载、加速度随时间的关系，还考虑了阻尼力的影响，得出地震过程中位移、应力、速度、加速度随时间的动力响应特征，一定程度上克服了拟静力法和滑块分析法的缺陷。

本文基于动力响应时程分析法，采用非线性有限元法，结合大岗山水电站坝址区右岸岩质边坡工程，并选取其典型剖面V-V进行动力响应特征分析，揭示了边坡动位移、动速度、动加速度、加速度放大系数及动应力的响应特征规律。

1 动力响应时程分析法

时程分析法（又称为 “直接动力法”或 “步步积分法”）是地震过程中体系反应随时间变化的过程。目前较常用的时程分析法有Wilson-θ法、Newmark-β法和线性加速度法，本文采用Wilson-θ法进行分析。

在地震作用下，可建立如下的动力平衡方程

式中，[M]、[C]、[K]分别为系统的总质量矩阵、总阻尼矩阵和总刚度矩阵；[u]、[u˙]、[u¨]分别为位移、速度和加速度矢量；[a]为输入的地面加速度。

假设系统服从瑞雷阻尼关系，则阻尼矩阵可表示为质量矩阵与刚度矩阵的线性组合

式中，α、β为瑞雷阻尼系数，若已知第i阶和第j阶固有频率分别为ωi和ωj，阻尼比分别ξi、ξj，则α、β可通过下式确定

Wilson-θ是在微小的时间段内建立引入参数 θ（θ>1）的线性加速度假设，在△t步长中进行增量分析，然后由线性内插求出反应增量，以此作为下一步计算初始条件。关于θ的取值问题，Wilson EL指出，当θ取值大于1.37时，即可使计算结果达到无条件稳定。目前，对一般工程进行时程分析计算时，常取θ=1.4，本文以此值作为计算取值。

2 工程实例

2.1 工程概况

大岗山水电站位于四川省大渡河中游石棉县境内，是大渡河干流近年来开发的大型水电工程之一，其工程场地50年超越概率10%的水平地震动加速度峰值为0.2517 g，相应地震基本烈度为VIII度，其右岸边坡为I级永久边坡。

右岸岩体由表向内可划分为全风化带、强风化带、弱风化带、微风化～新鲜岩体。根据岩体卸荷发育程度，可划分出强弱卸荷带。自然坡度一般40°～65°，1220 m高程以上的斜坡地形较缓，地表基本上为崩坡积层（Qdl+col4）所覆盖，水平厚度10～20 m，垂直厚度10～15 m；1220 m高程以下地形稍陡，由花岗岩构成陡壁。1200～1300 m高程以上基岩为灰白色、微红色中粒黑云二长花岗岩，局部出露辉绿岩脉、花岗细晶岩脉等；1250 m高程以上分布有一定厚度的崩坡积层。据勘探揭示，边坡发育断层 82条，以F1、f191、f174规模相对较大，同时还发育78条辉绿岩脉和8条花岗细晶岩脉，主要有β4、β97、β146、β168、β202等岩脉破碎带，岩脉破碎带呈块状、碎裂结构。

2.2 计算模型及边界条件

由于地震影响范围较广，为消除边界条件对计算结果的影响，应尽量将计算边界取得足够远。结合坝址区右岸岩质边坡的地形地质条件，动力分析计算范围确定为:顺河向（X轴，上游为正）距坝轴线上、下游各取400 m，共800 m；横河向（Y轴，指向右岸为正）左至河谷左岸114 m，右至河谷右岸686 m，共800 m；最大高度（Z轴，垂直向上为正，由600 m高程延伸至地表）近1000 m。岩体、断层、裂隙均采用8节点等参实体单元模拟，其接触面采用8节点夹层单元模拟，整个计算域共离散为133265个节点和127494个单元。岩质边坡三维计算模型见图1。

图1 边坡三维计算网格

整个计算区域从坝址区上游向下游平行于Y轴方向共有9个典型剖面，根据边坡的工程地质条件及对坝址区域影响程度等因素，选取V-V剖面作为模型的计算主剖面，该剖面围岩类别分布见图2。为避免地震波在边界上反射，计算模型底部边界设置为刚性边界，周边边界设置为粘弹性边界，借此模拟散射波辐射及地基弹性恢复性能。根据工程地质勘察报告，该边坡各岩层物理力学参数见表1。

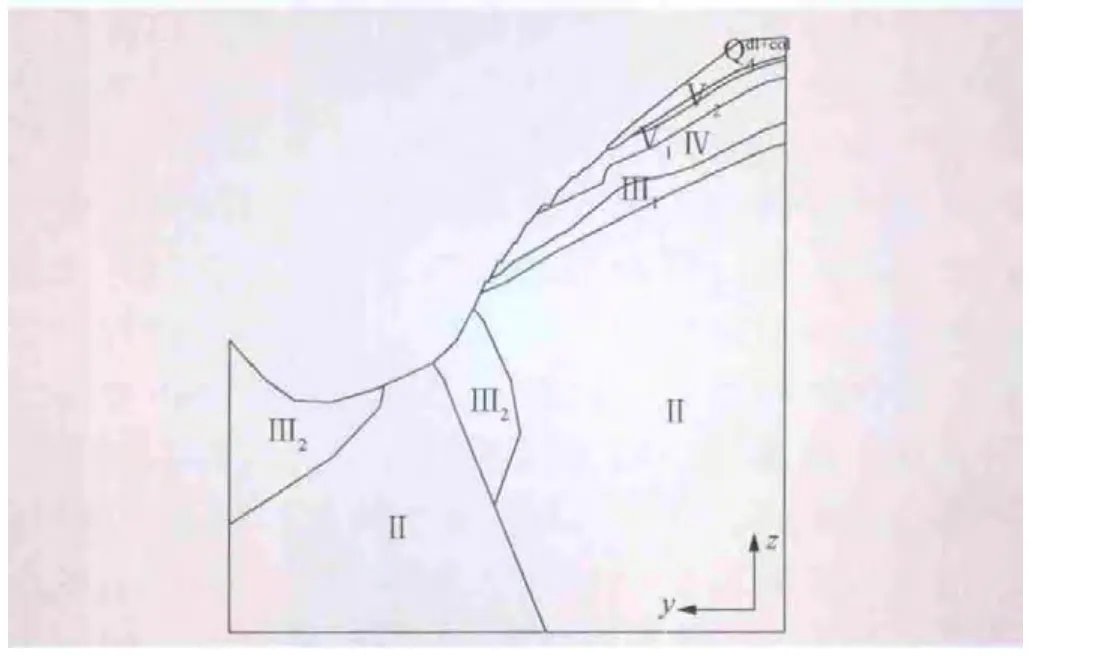
图2 V-V典型剖面

2.3 输入地震加速度

对边坡的地震反应分析时考虑水平与竖向震动的共同作用较为合理，根据动力模型的模态分析结果，选取固有频率 f1＝1.1497、f2＝1.1895，相应 ω1=2πf1、ω2=2πf2，阻尼比 ξ1=ξ2=ξ=0.05，根据公式（3）可得瑞雷阻尼系数α＝0.3673、β＝0.0068。地震加速度时程见图3。顺河向峰值加速度为3.221m/s2，横河向为3.213 m/s2，竖直向为2.118 m/s2。计算时间步长取0.02 s，地震波历时24 s。按规范，动弹性模量取为静弹性模量的1.3倍，泊松比保持不变。

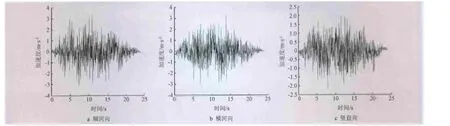
图3 地震加速度

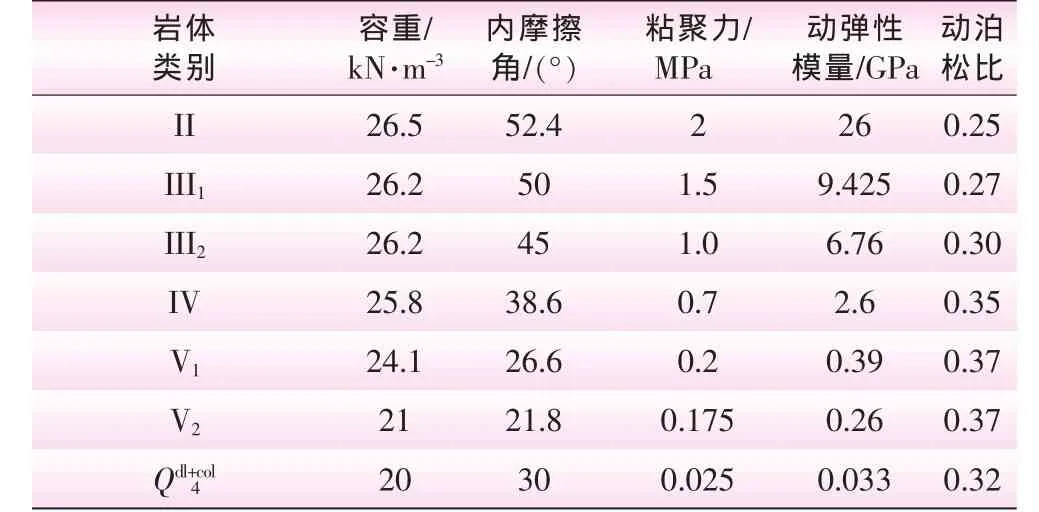
表1 主要岩体物理力学参数

3 岩质高边坡动力响应

3.1 边坡动位移分布规律

动位移最大响应等值线见图4。在地震持续过程中（T=24 s），边坡横河向和竖直向动位移极值分布特征:①总体上均呈现随高程递增而递增的趋势，在接近坡顶表面处达到最大，最大横河向动位移极值10.55 cm，最大竖直向动位移极值8.34 cm；②同一高程，崩坡积层以下，岸坡横河向动位移极值基本相同；崩坡积层以上，横河向动位移极值由岸坡向深部递减，而竖直向动位移极值呈现出岸坡大于深部的特征；③在崩坡积层范围内，横河向与竖直向动位移极值相对于边坡其他部位均有较大增幅，这主要是由于坡顶崩坡积层弹性模量较低。

3.2 边坡动速度响应规律

动速度最大值响应等值线见图5。在地震作用下，边坡动速度有如下规律:①随着高程的增加，边坡横河向和竖直向动速度均呈现出增大的趋势，最大值分别为0.6、0.43 m/s，均在崩坡积层表面处达到最大；②同一高程，岸坡横河向和竖直向动速度均表现为沿坡面向坡内递减的趋势；③崩坡积层范围内，由于其动弹性模量相对较小，横河向和顺河向动速度均较边坡其他部位量值显著增大。

图4 动位移最大值响应等值线（单位:cm）

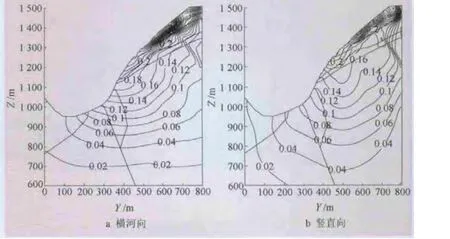
图5 动速度最大值响应等值线（单位:m/s）

3.3 边坡动加速度响应规律

由边坡动加速度最大值响应等值线（见图6）和加速度放大系数等值线（见图7）可以看出:①沿着高程增加方向，横河向和竖直向动加速度均呈现递增的趋势，最大值分别为7.88、5.83 m/s2，出现部位均为崩坡积层与V1类岩体坡面相交处，加速度放大系数分别为3.34和2.76。随着高程增加，加速度放大系数呈增大趋势。②同一高程，横河向与竖直向动加速度表现为由岸坡向深部递减的趋势。③由于崩坡积层变形参数很低，崩坡积层中动加速度变化梯度较大。

图7 动加速度极值放大系数等值线

3.4 边坡动应力响应规律

图8 动应力最大值响应等值线（单位:MPa）

动应力最大值响应等值线见图8。地震荷载作用下，边坡岩体的最大和最小动主应力极值呈现出如下特征:①边坡岩体动应力极值总体上呈现出深部大于浅部的特征，大主应力极值为0.8～18.4 MPa，小主应力为－1.7～4.6 MPa。同一高程，大主应力极值与小主应力极值总体上呈现出由岸坡向深部递增的趋势；②边坡拉应力分布区主要集中在岩层分界线及坡腰表层处，拉应力区扩展。在边坡坡面浅部约1000～1150 m高程范围内出现拉应力区，最大值为1.7 MPa，在此范围内应加强支护措施。

3.5 边坡特征点响应分析

图9 特征点动力响应时程

图9给出了1260 m高程（坡腰部位）边坡坡面特征点的动应力、动位移、动速度和动加速度响应时程。从动应力时程分布来看，大小主应力分布范围约－1.6～2.3 MPa，动应力反应的最大时段大约在5.2～11 s之间，由于材料阻尼作用与输入相对加速度并不同步，存在一定的 “滞后效应”；边坡动位移、动速度和动加速度均以横河向为主，其最大反应时段约是5.2～11、5.2～13.4 s和5.2～12.5 s之间，较输入加速度均存在一定 “滞后效应”，随着地震加速度增加，边坡相应的动力响应明显增强。