重力坝胶结面抗滑稳定性的综合评价方法
2014-10-21马福恒陆明志储冬冬
胡 江,马福恒,陆明志,储冬冬
(1.南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏 南京 210029;2.江苏省水利科学研究院,江苏 扬州 225002)
0 引 言
结构可靠度分析包括失效模式的确定和给定不同荷载下的响应概率的计算,涉及结构性态的确定性分析和可靠度的数学分析两方面的理论。结构缺陷、材料病害和基础老化都可能导致系统出现安全问题,采用非线性本构模型和动态分析方法得到的结果更符合实际,为此,结构的可靠度分析正向基于非线性分析的失效模式确定和失效概率的精确计算方向发展。苏怀智等[1]探讨了变量相关性对重力坝可靠度计算结果的影响;李典庆等[2]提出了边坡可靠度分析的随机响应面法;朱建明等[3]利用Rosenbleuth法和随机动分析方法求解了重力坝深层抗滑稳定的可靠度;章青等[4]采用接触面应力单元法分析了胶结面抗滑稳定性;Altarejos-García、陈祖煜等[5-6]证明了传统方法与可靠度方法相对安全率的等价性。
混凝土与基岩胶结面是重力坝和基岩相互作用的纽带,其抗滑稳定分析是重力坝安全评价的主要内容。胶结面存在显著的非线性效应,传统方法多采用抗剪或抗剪断解析式分析评价其抗滑稳定性,与实际工作性态差异较大。本文在传统方法的基础上,结合非线性有限元可靠度分析方法,提出了胶结面抗滑稳定安全的多级多方法综合评价体系,以更全面更准确地掌握重力坝的实际性态。以某在役工程为例,在提出评价体系下,融合弹塑性Mohr-Coulomb模型、响应面法 (RSM),考虑多种变量分布形式及相关性的可靠度计算方法,探讨分析了胶结面抗滑稳定可靠度和传统安全系数间的关系。
1 综合评价方法
将综合评价方法分为5个阶段,综合应用可靠度分析和非线性确定性分析方法,建立如图1所示的多级分析框架体系。
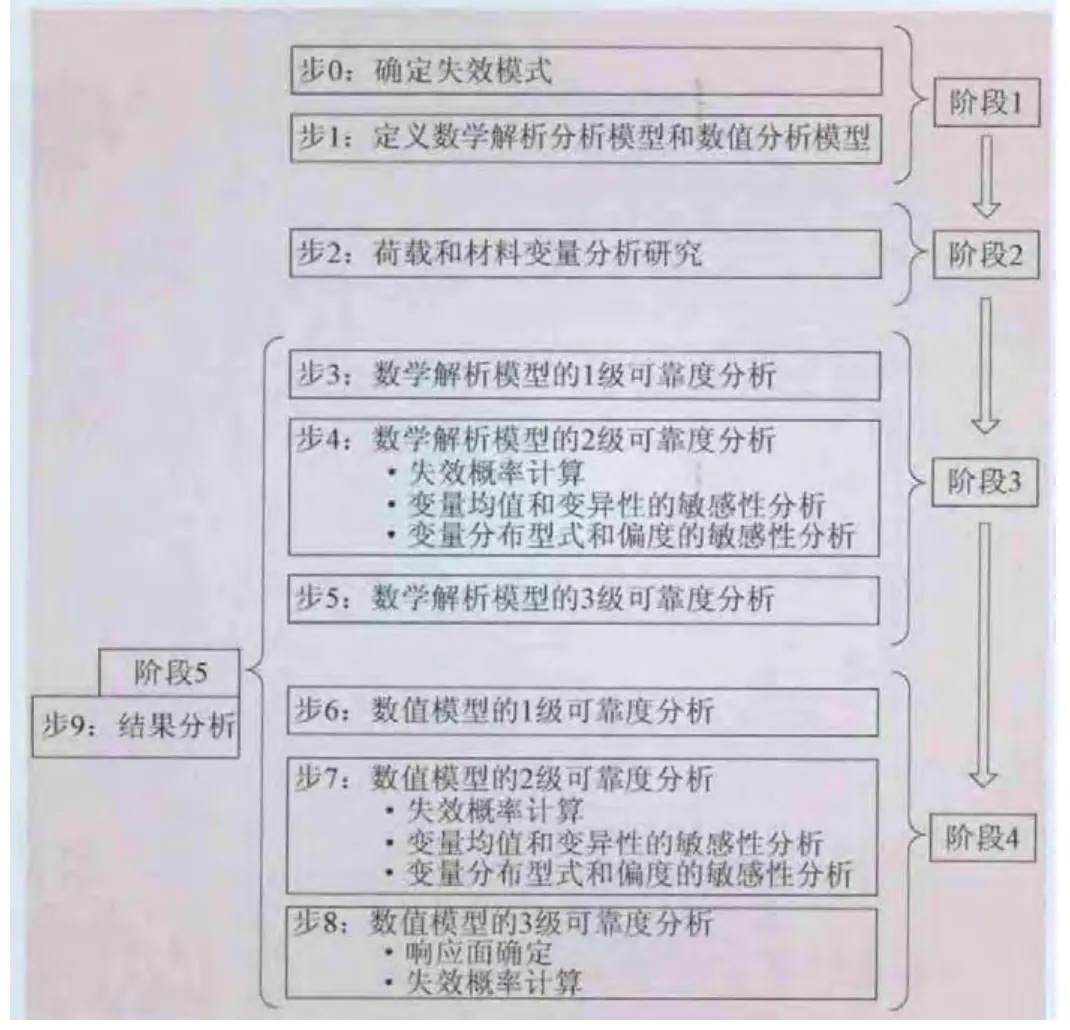
图1 多步骤多级多方法重力坝安全综合评价方法
1.1 确定数学解析和数值分析模型 (步骤1)
分析荷载工况并识别可能的失效模式后分别确定数学解析模型和数值分析模型。数学解析模型为失效模式所对应的极限状态函数,数值分析模型为非线性本构模型。
1.2 变量分析 (步骤2)
对荷载和材料参数进行分析研究,将各变量按确定性、较低不确定性、随机变量分类。其中,随机变量应通过实验数据、已有经验的建议值等综合确定其特征值[6-7]。
1.3 基于数学解析模型的可靠度分析
1.3.1 1级可靠度分析 (步骤3)
1级可靠度分析,即安全系数计算。依据变量的均值,采用传统刚体极限平衡法计算安全系数。
1.3.2 2级可靠度分析 (步骤4)
2级可靠度分析,即采用FORM分析结构可靠度。主要包括失效概率计算及其对各变量的变异系数及分布型式偏度的敏感性分析等方面。
失效概率pf的计算式为
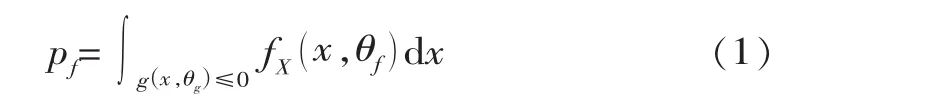
式中,X为n维随机变量矢量;fX(x,θf)为联合密度函数,其中θf为分布参数矢量;g( x,θg)为确定性的极限状态函数,其中的矢量x由随机变量矢量X和θg得到,g( x,θg)≤0为失效域。
式(1)中的联合密度函数fX(x,θf)一般未知,可通过Nataf变换利用变量的边缘概率密度函数、随机变量间的Gaussian相关结构构造变量联合概率密度函数。将原始相关随机变量X转换为相关标准正态分布随机变量Z,其相关结构服从式(3)表示的积分关系,再由Z转换为不相关的标准正态分布随机变量U,转换过程用式(2)表示
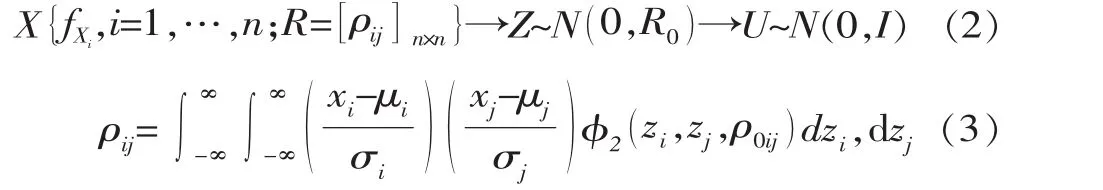
式中,μi和σi分别为X中的第i个变量的均值和标准差;φ2(·,·,ρ)为相关系数为ρ的二维标准正态概率密度函数。文献[8]研究了常用分布形式时式(3)的解,本文采用二维Gauss积分求解。
对于相关性为ρij的变量对ij,由式(3)确定映射得到的矢量z中变量间的相关性ρ0ij。从而可以由Z通过式(4)转换得到不相关标准正态随机变量

式中,L0为矩阵R0=[ρ0ij]的Cholesky分解的下三角矩阵,即=R0。
FORM法在标准空间中寻找极限状态函数的最可能失效点P*(MPP)(设计点)的一阶近似值,其实质是求解下式表示的约束最优化问题
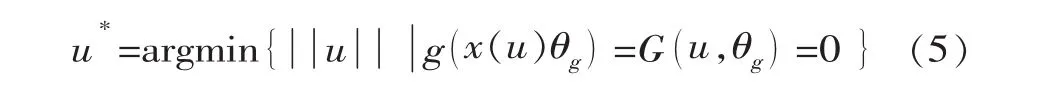
获得P*后,即可计算得到可靠度指标β=αTu*其中α=为P*点的负法向梯度矢量;由可靠度指标可以得到失效概率pf1=Φ(-β),其中Φ(·)为标准正态累积密度函数。同时,还可以得到可靠度指标对参数统计特征值的敏感性,如β对θf的敏感性为
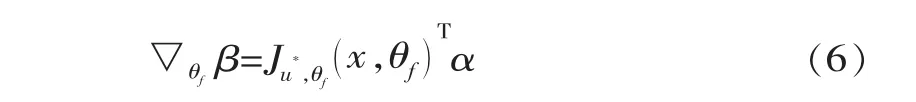
对式(4)求θf的变分得到Jacobian变换,即

敏感性分析同样通过积分方案得到,方法同获得矩阵R0一样。
1.3.3 3级可靠度分析 (步骤5)
3级可靠度分析,即采用FORM对失效概率的分析和计算。基于步骤4分析得到的失效概率对变量统计特征值的敏感性,计算由敏感性较高的随机变量组成的变量矢量下的失效概率。
1.4 基于数值模型的可靠度分析
1.4.1 1级可靠度分析 (步骤6)
同1.3,在可靠度分析前,首先采用非线性数值模型计算得到安全系数,以此初步验证和比较解析和数值两种模型,并为网格细化提供依据。
采用弹塑性Mohr-Coulomb模型计算抗滑稳定安全系数时,胶结面稳定的整体安全系数Fs表示为[9-10]
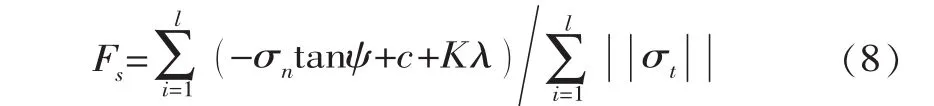
式中,tanψ和c分别为摩擦系数和粘聚力;σn和σt分别为法相和切向应力;l和s分别为胶结面的长度和单元大小;K为硬化参数;λ为累积塑性切向位移。
1.4.2 2级可靠度分析 (步骤7)
综合采用FORM和数值模型分析结构可靠度。如能够获取显式状态函数,以下方法同1.3.2。
1.4.3 3级可靠度分析 (步骤8)
一般很难显式获取极限状态函数,需借助响应面来解决这一问题。生成变量集对,通过对数值分析结果的拟合得到响应面,避免过多地调用非线性数值计算程序。真实的极限状态函数g(X)用多项式响应面函数(X)表示,对于X,含交叉项的二元多项式为
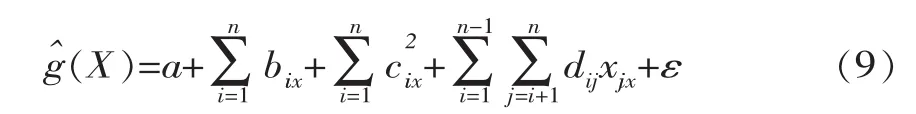
式中,a、bi、ci和dij为多项式系数;ε为随机误差。由于交叉项使函数包含了大量变量,实际应用时,一般采用不含交叉项的二元多项式响应面函数,一些情况下,则采用简单线性函数来代替真实的响应面函数
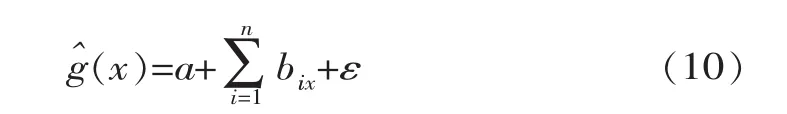
响应面法的实质是一种统计学方法,有星形、完全析因、中心复合、Box-Behnken等多种抽样方法可以用来确定样本点,图2表示了3个随机变量时各种设计方法的取点情况。样本点在以均值为中心标准差为大小的区间范围选取,即xi=μi∓σi。得到对应于样本点的结构响应后,通过最小二乘法拟合得到响应面函数系数。
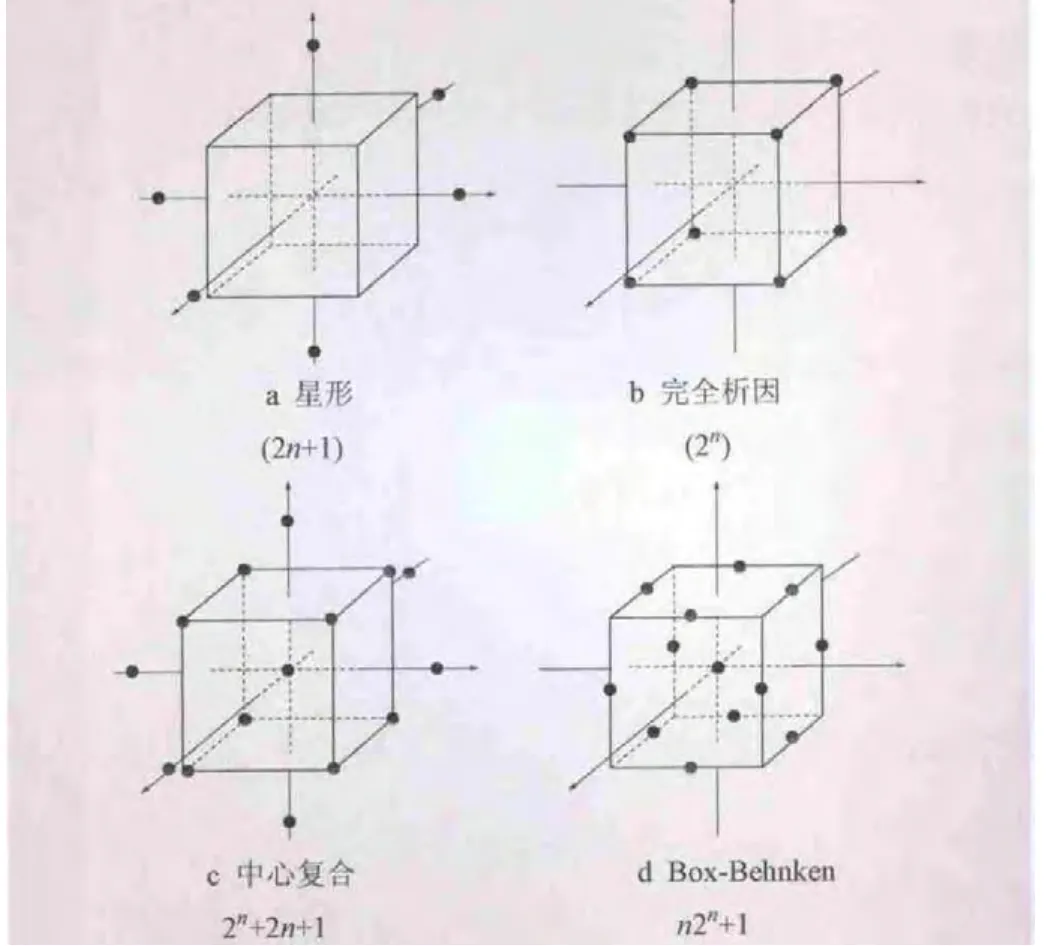
图2 随机变量样本点设计方法 (n=3)
将胶结面的滑移失效视为各个单元失效事件的并联组合。本文对系统失效概率的计算采用矩阵积分的方式,由m个单元失效模式组成的并联系统失效概率 psys为
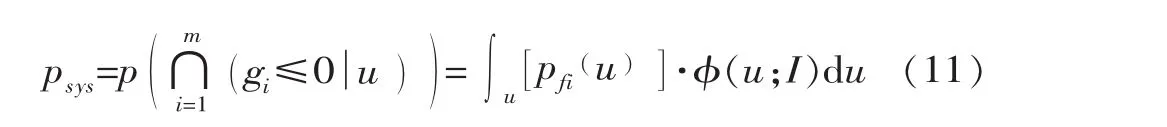
1.5 结果分析 (步骤9)
分析由上述多步骤多级多方法综合评价方法得到的系列结果,包括结构本身及分析过程中涉及的多种不确定性对安全评价结果的影响等。
2 工程实例
2.1 工程概况
以一重力坝的溢流坝段为例 (见图3),分析不同库水位工况下的胶结面抗滑稳定状况。堰顶高程73.0 m,坝顶高程82.5 m;正常蓄水位80.0 m,下游水位26.0 m。图3中所示库水位从低到高 (28~91.7 m)超越概率依次为1、0.8、0.556、0.357、3.23×10-4、1.20×10-6和 4.00×10-9。
2.2 确定数学解析和数值分析模型
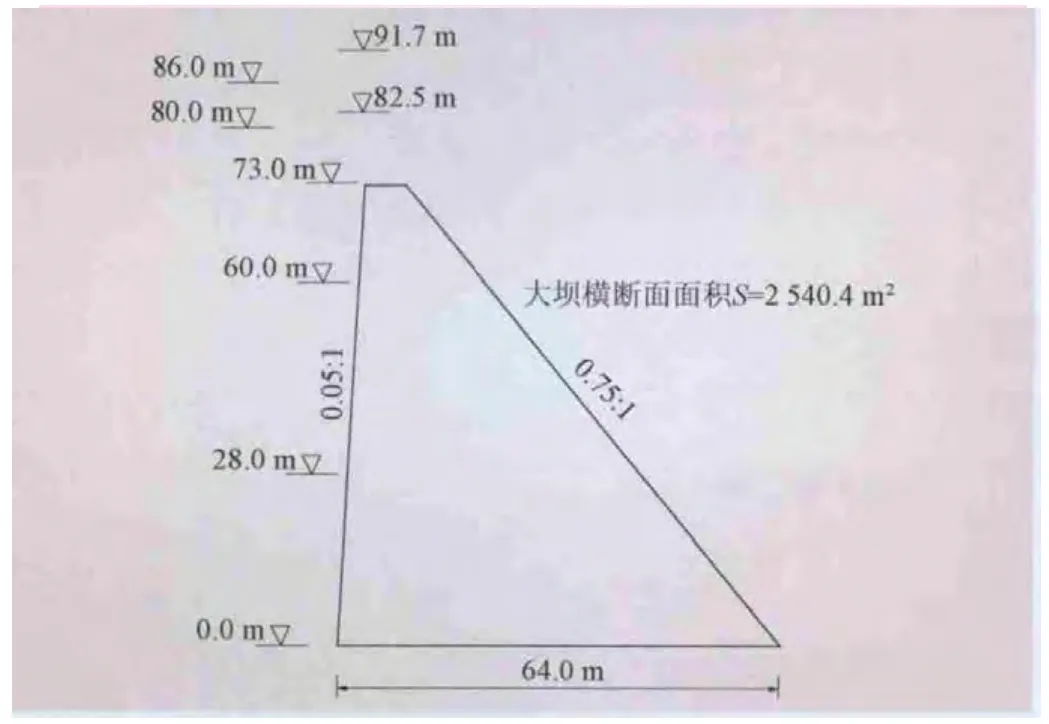
图3 溢流坝横截面和库水位示意
采用Mohr-Coulomb模型,极限平衡状态为粘聚力c和摩擦系数ψ的函数确定数学解析解。采用薄层节理单元和弹塑性Mohr-Coulomb模型分析胶结面性态,并视坝体和坝基为变形体建立数值仿真模型计算分析。根据参考文献[10]胶结面厚度取0.1 m。有限元网格范围为上下游延伸120.0 m,基岩深80.0 m,胶结面分为64个单元。
2.3 变量分析
假设坝基扬压力折减系数α呈均匀分布。胶结面抗剪断系数ψ和c分别呈正态和对数正态分布,且两者存在强的负相关性,假定两者不相关时,计算结果偏保守,符合工程实际需要。根据试验数据、实测信息,得到计算所需参数见表1。
2.4 基于数学解析模型的可靠度分析
(1)1级可靠度分析。采用Mohr-Coulomb模型,建立抗滑稳定极限状态函数
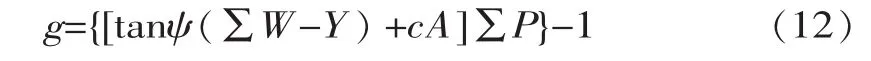
式中,∑W和Y分别为作用在胶结面上的总重力和扬压力;∑P为作用在坝体的水平合力;A为胶结面面积;其他符号同式(8)。对应不同库水位,代入变量的均值,水位从60.0 m起从低到高依次计算得到胶结面抗滑稳定的安全系数分别为 5.08、3.14、2.52、2.34、2.12和1.82。
(2)2级可靠度分析。采用FORM计算由式(13)表示的胶结面抗滑稳定失效概率,得到的失效概率如图4所示。失效概率对各随机变量统计特征值的敏感性结果见图5。
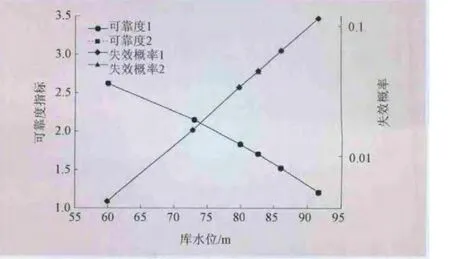
图4 不同水位下的可靠度和失效概率(1:多随机变量;2:少随机变量)
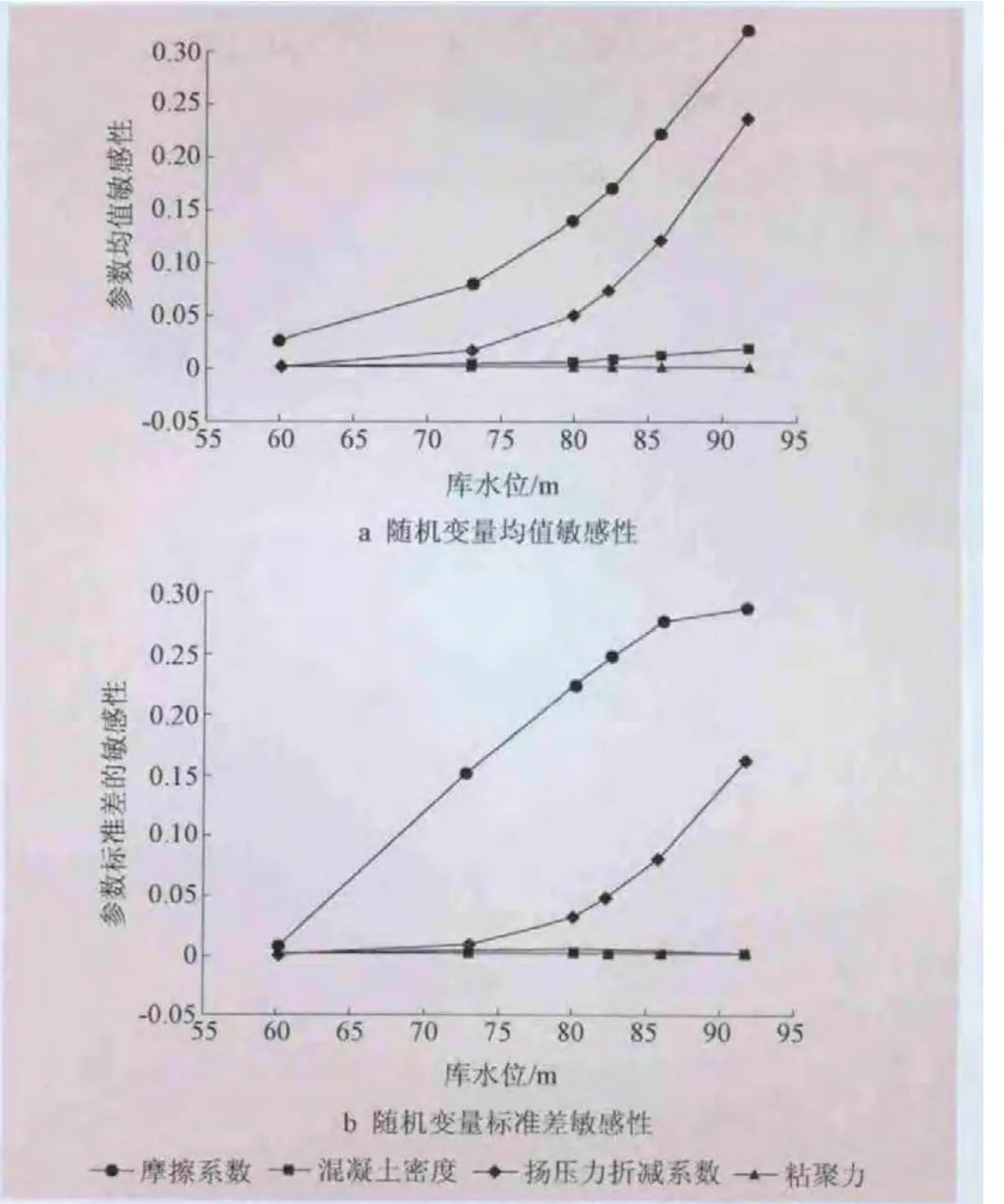
图5 失效概率对随机变量的敏感性
(3)3级可靠度分析。由图6可以看出,胶结面抗滑失稳的概率对ψ和α的均值和标准差都较为敏感,且随机变量的敏感性随库水位不同而有所差异。仅考虑这两个随机变量,重新计算得到胶结面抗滑失稳的可靠度和失效概率,结果如图5,可以看出两种情况下得到的结果几乎相等。本文暂不考虑不同随机变量的分布型式对失效概率的影响。

表1 计算参数
2.5 基于数值模型的可靠度分析
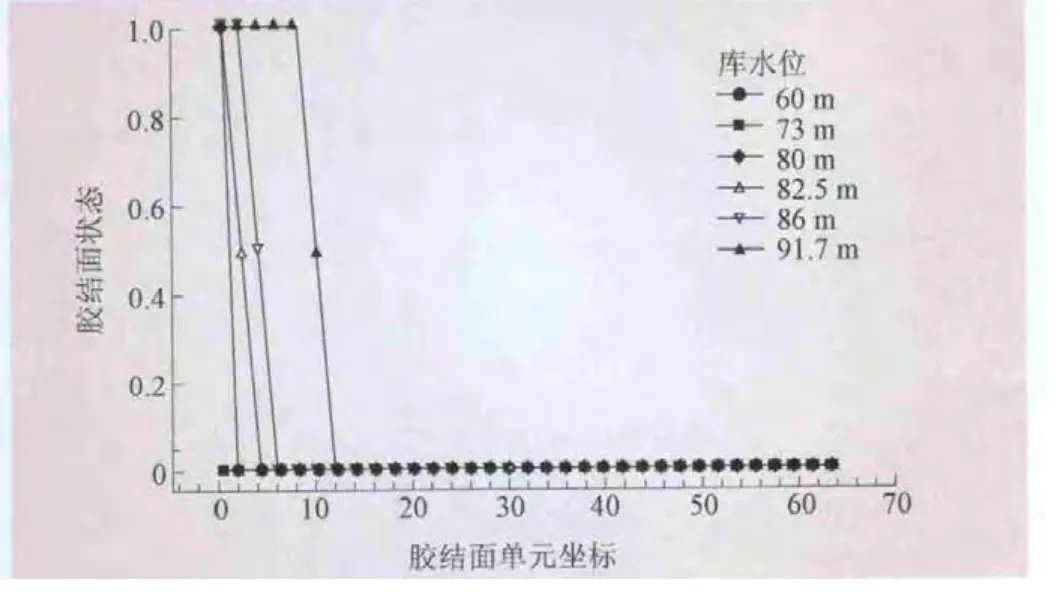
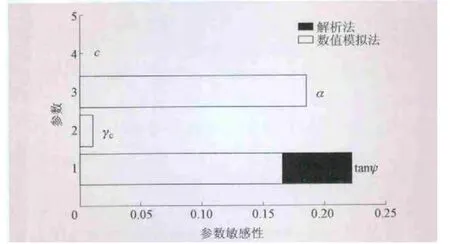
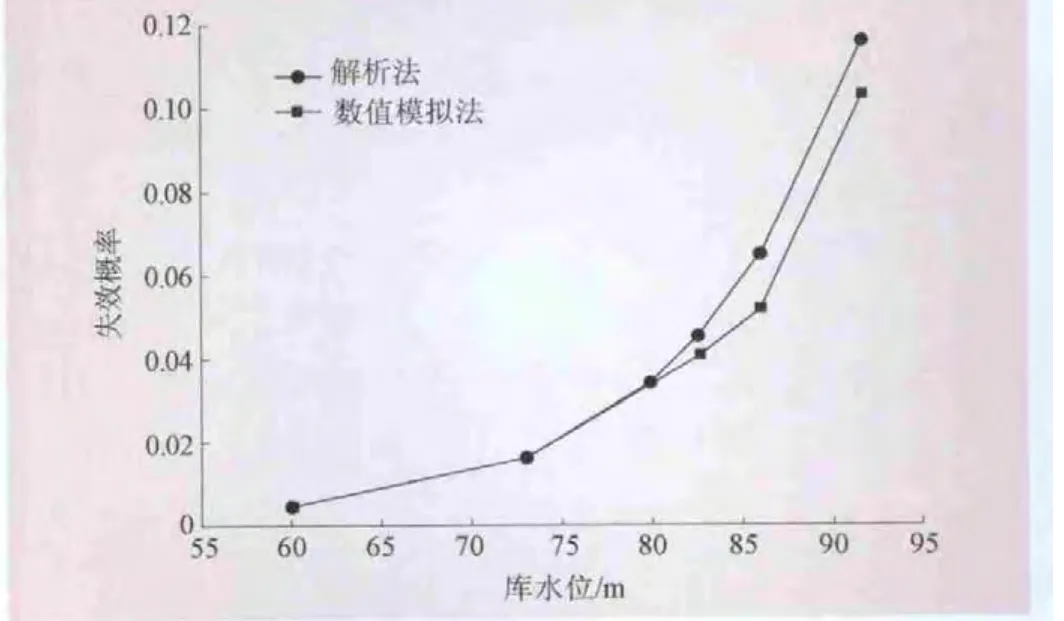
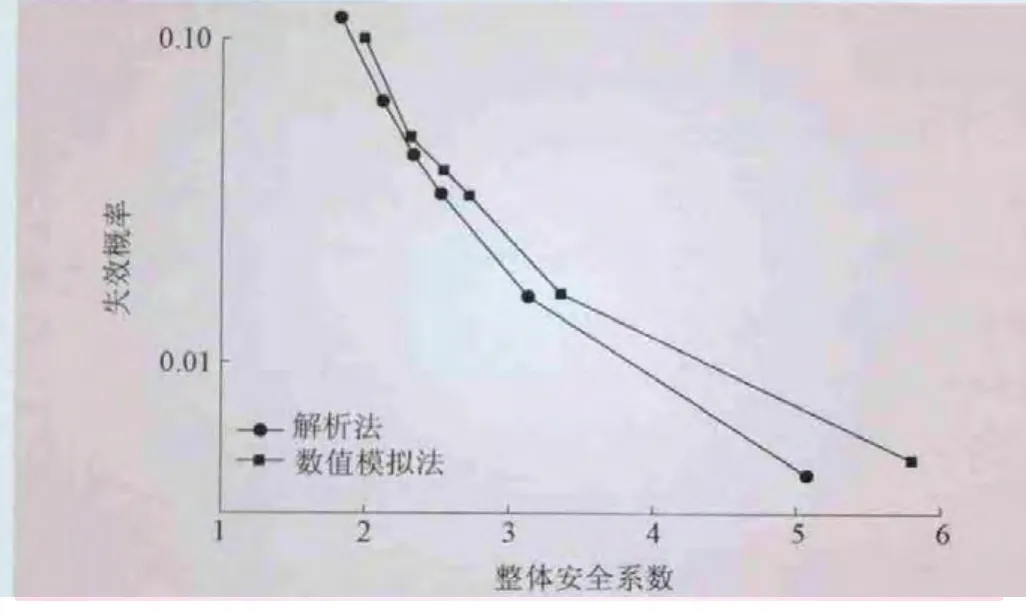
(1)1级可靠度分析。采用数值分析方法,据式 (8)分别计算不同库水位下的胶结面单元的局部安全系数和整体安全系数,结果分别如图6、7所示。以法向应力是否超过允许抗拉强度为标准,判断胶结面是否开裂,即以σn 图6 胶结面单元的局部安全系数 图7 不同水位下的整体安全系数 图8 不同库水位下的胶结面开裂状态 (2)2、3级可靠度分析。采用完全析因法作为随机变量样本点的设计方法,采用响应面法拟合胶结面的抗滑状态响应。经过试算发现,胶结面抗滑稳定各失效单元间存在高度的相关性,按整体考虑胶结面的抗滑失稳。随机变量为胶结面的抗剪断参数ψ、c、α和混凝土容重γc,一个胶结面单元失效的数值分析次数为24=16次。以库水位86.0 m为例,将数值分析得到的结果,采用式 (10)表示的一次函数拟合,得到响应面函数为 该函数拟合精度为0.987,即一次函数式就可以较好地反映所考虑荷载下的胶结面工作性态。采用FORM计算得到失效概率为0.051,略小于基于数学解析模型计算得到的失效概率0.0645。比较步骤4和步骤7两种情况下的参数的敏感性,见图9;得到的设计点分别为 [0.627,23.467,0.695,213.16]和[0.646,23.457,0.797,209.51]。 按照相同方法,计算得到其他库水位下的胶结面抗滑失稳概率,结果见图10。 图9 两种计算方法下的参数敏感性比较 图10 两种计算方法不同库水位下的胶结面失稳概率 整体上看,在高库水位下,步骤3~5中的基于传统方法 (极限平衡法)可靠度分析方法计算得到的胶结面安全系数较步骤6~8中的基于数值模拟的可靠度分析方法小,抗滑失稳概率稍大。在低库水位下,两者计算得到的结果基本吻合,基于数值模拟可靠度分析方法结果甚至稍高。这是因为在高库水位下,合理厚度的薄层节理单元能较好地反映胶结面的应力-应变状态,应力集中导致坝踵处的胶结面容易开裂;胶结面应力状态越均匀,强度储备越大;坝趾坝踵处应力越集中,强度储备越小。 从参数的敏感性分析可以看出,在较低库水位下,参数的敏感性分析不合理,因此参数敏感性分析时应当选择合理的库水位。选用敏感性较高的参数作为随机变量,计算结果几乎与考虑敏感性较低随机变量在内的所有变量的结果相等。安全系数和失效概率间的关系如图11所示,可知即使在较高的安全系数下,胶结面仍然存在较高的失稳概率,这表示胶结面安全分析过程中存在较大的不确定性。因此,对于大坝安全管理和补强加固决策,现场试验和工程检测十分必要,这样可以提高随机变量统计特性的准确性,同时减少数据处理过程中的主观模糊性。 图11 安全系数和失效概率的关系 综合极限刚体平衡法、基于解析式的可靠度分析方法、非线性有限元可靠度分析方法以及响应面法等确定性方法和概率方法,提出了多级多方法混凝土坝安全综合评价体系。通过工程实例的分析,得到如下结论: (1)安全系数较高的情况下,失效概率不一定低,混凝土坝的安全分析应综合采用多种方法。基于数值模型的可靠度分析结果能较好地反映结构的失效机理和失效过程;传统的解析方法结果较为保守。将 “混凝土坝-胶结面-基岩”视为系统,分别采用合理的非线性本构模型,分析一定荷载下的结构系统的响应,可以获得更加真实的失效概率。 (2)失效概率分析的过程中,随机变量的分析十分重要。敏感性较高的随机变量的均值和标准差都可能导致失效概率出现较大变异。应当充分挖掘工程资料、试验数据和检测数据,并结合现有文献研究成果对随机变量尤其是敏感性较高的随机变量取值。 [1]SU Huaizhi,HU Jiang,WEN Zhiping.Service Life Predicting of Dam Systems with Correlated Failure Modes[J].Journal of Performance of Constructed Facilities,2013,27(3):252-269. [2]李典庆,周创兵,陈益峰,等.边坡可靠度分析的随机响应面法及程序实现[J].岩石力学与工程学报,2010,29(8):1513-1523. [3]朱建明,张宏涛,陈祖煜.重力坝深层抗滑稳定可靠度分析研究[J].岩土工程学报,2008,30(10):1444-1448. [4]ZHANG Qing,WANG Zhiqiang,XIA Xiaozhou.Interface stress element method and its application in analysis of anti-sliding stability of gravity dam[J].SCIENCE CHINA Technological Sciences,2012,55(12):3285-3291. [5]ALTAREJOS-GARC?A L,ESCUDER-BUENO I,SERRANO-LOMBILLO A,et al.Methodology for estimating the probability of failure by sliding in concrete gravity dams in the context of risk analysis[J].Structural Safety,2012,36-37:1-13. [6]陈祖煜,徐佳成,孙平,等.重力坝抗滑稳定可靠度分析:(一)相对安全率方法[J].水力发电学报,2012,31(3):148-159. [7]SU Huaizhi,HU Jiang,WEN Zhiping.Structure analysis for concrete-faced rockfill dams based on information entropy theory and finite element method[J].International Journal for Numerical and Analytical Methods in Geomechanics,2012,36(8):1041-1055. [8]LIU Peiling,KIUREGHIAN A D.Multivariate distribution models with prescribed marginals and covariances[J].Probabilistic Engineering Mechanics,1986,1(2):105-112. [9]郑颖人,赵尚毅.用有限元法求边坡稳定安全系数[J].公路交通技术,2002(1):7-9. [10]杨 杰,吴中如,顾冲时,等.坝体与坝基材料参数的薄层单元有限元反分析[J].岩石力学与工程学报,2006,25(增 1):3087-3092.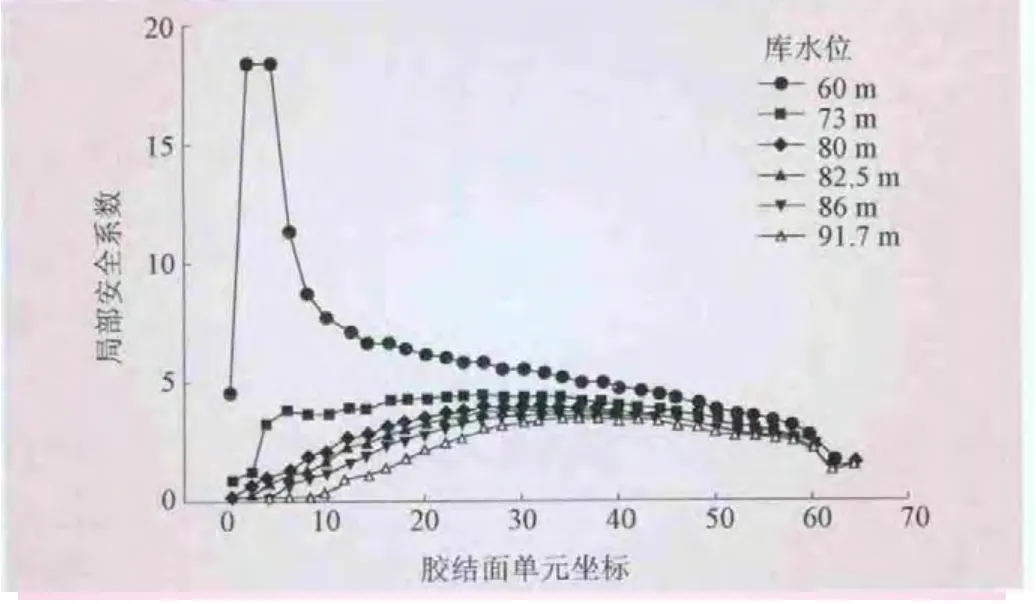

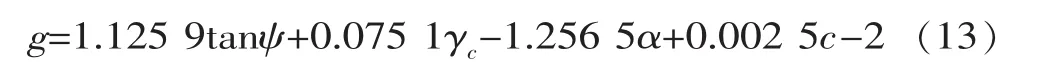
2.6 结果分析
3 结论
