衰减记忆平方根UPF算法及其在组合导航中的应用

(1.西北工业大学 自动化学院，西安 710072；2.航天恒星科技有限公司，北京 100086)

(1.西北工业大学 自动化学院，西安 710072；2.航天恒星科技有限公司，北京 100086)

针对用UPF算法进行导航滤波计算可能出现协方差矩阵不对称或负定的问题，在研究衰减记忆滤波和平方根滤波的基础上，以Unscented粒子滤波为框架，提出一种新的衰减记忆平方根UPF算法。该算法利用衰减因子减小历史信息对滤波的影响，增强当前量测信息在滤波计算中的作用。然后，以协方差矩阵的平方根阵代替协方差矩阵进行滤波解算，保证了协方差矩阵的对称性和非负定性，提高了滤波算法数值稳定性和解算精度。将提出的算法应用到SINS/SAR组合导航系统中进行仿真验证，并与UPF算法进行比较，结果表明，提出算法的滤波性能明显优于UPF算法，能提高组合导航系统的滤波精度。

衰减因子；平方根滤波；衰减记忆滤波；Unscented粒子滤波；协方差矩阵

卡尔曼滤波 (Kalman Filter，KF)将状态空间思想引入到最优滤波理论中，用状态方程描述系统动态模型，用观测方程描述系统观测模型，可处理多维信号、非平稳信号和时变信号的滤波问题，在工程实际中得到了广泛应用。但卡尔曼滤波要求已知系统精确的数学模型，且要求系统模型为线性，噪声信号为统计特性已知的高斯噪声，这大大限制了KF的应用[1]。

为了克服 KF的缺陷，一些学者研究提出了扩展卡尔曼滤波(EKF)，其基本思想是将非线性系统模型进行Taylor展开，略去二阶项以及二阶以上的高阶项，得到非线性系统的线性化模型，然后对线性化后的系统模型采用卡尔曼滤波算法进行计算。EKF虽然在非线性滤波中得到了广泛应用，但略去Taylor展开式的高阶项会引起较大的线性化误差，导致滤波误差增大甚至发散。

Julier等人提出了无迹卡尔曼滤波(Unscented Kalman Filter，UKF)算法，UKF通过无迹变换(Unscented transformation，UT)对非线性系统状态的后验概率密度函数进行近似。与EKF相比，UKF无需计算非线性状态函数和量测函数的雅克比矩阵，且理论上可以实现泰勒级数三阶项所达到的精度，具有计算简单，收敛性好等优点。然而，在噪声先验统计特性未知的情况下，UKF滤波精度会下降甚至发散。

Fagin和Sorenson提出了衰减记忆滤波算法[2-3]，该算法通过衰减因子限制卡尔曼滤波器的记忆长度，减小历史信息对滤波的影响，增强当前量测信息在滤波计算中的作用，从而提高了滤波精度。但是，该方法要求计算矩阵的特征值和迹，计算量较大。平方根滤波算法采用矩阵分解的方法，在滤波过程中不计算协方差矩阵，而是用协方差矩阵的平方根阵代替协方差阵进行迭代运算，解决了常规算法中由于计算误差和噪声信号等因素引起协方差矩阵不对称或负定而导致的滤波发散问题[4-5]，保证了协方差矩阵的非负定性，其缺点是计算量比标准的滤波计算大[6-9]。

本文在研究衰减记忆滤波和平方根滤波的基础上，以Unscented粒子滤波为框架，提出一种新的衰减记忆平方根 UPF (Fading Memory Square Root Unscented Particle Filter，FMSRUPF) 算法。该算法利用衰减因子减小历史信息对滤波的影响，增强当前量测信息在滤波计算中的作用。然后，以协方差矩阵的平方根阵代替协方差矩阵进行滤波解算，保证了协方差矩阵的对称性和非负定性，提高了滤波算法数值稳定性和解算精度。将提出的算法应用到SINS/SAR组合导航系统中进行仿真验证，并与UPF算法进行比较，结果表明，提出算法的滤波性能明显优于UPF算法，能提高组合导航系统的滤波精度。

1 一种衰减记忆平方根UPF算法

考虑非线性系统：

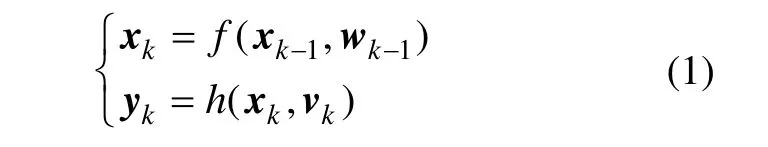
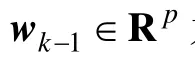
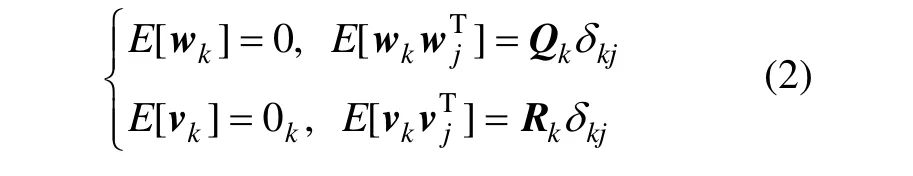
式中， Qk和 Rk分别为噪声 wk和 vk的协方差矩阵，δkj为Dirc函数。

衰减记忆平方根UPF算法的流程如图1所示。

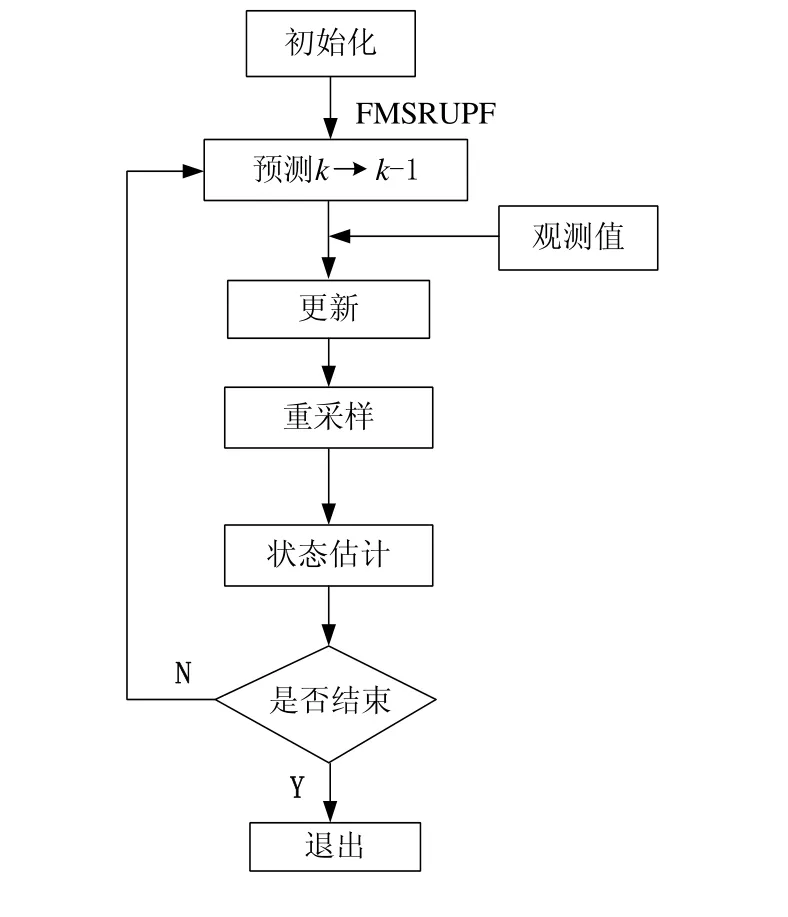
图1 衰减记忆平方根UPF算法流程图Fig.1 Architecture for fading memory square root unscented particle filter

计算步骤为：

第一步：初始化

第二步：用FMSRUPF滤波器更新粒子(k=1,2,…,n)

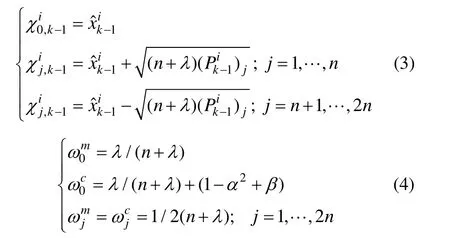
2）构造衰减因子 αk

衰减因子的确定方法不唯一。一些学者按滤波器收敛判据选择衰减因子，要求理论预计误差大于实际误差[10]。另一些学者在自适应算法中用“记忆长度”决定衰减因子，当估计误差较大时选用较大的衰减因子，反之则选择小的衰减因子。文献[11]提出了一种新的衰减滤波算法，推导出两类衰减因子：第一类是用最速下降法确定衰减因子，计算时需经过多次迭代，且公式复杂，计算过程复杂，不适合工程实际应用；第二类衰减因子采用一步算法，其解析式为

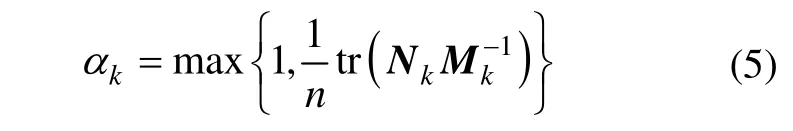
式中， αk为衰减因子，tr[·]为矩阵求迹符号，n为粒子数， Mk和 Nk的表达式分别为[12]

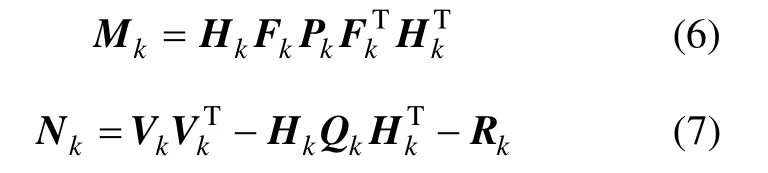
3）时间更新

式中，qr{·}表示矩阵的QR分解，αk为衰减因子。

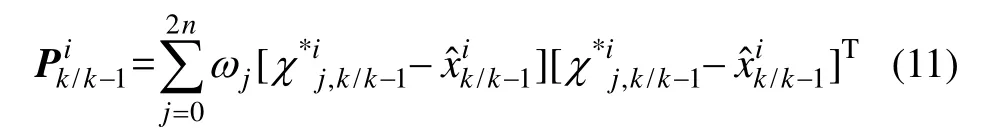
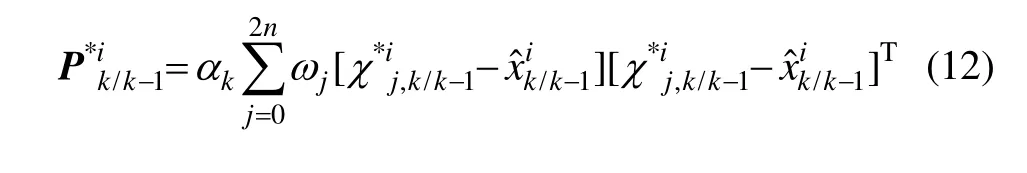
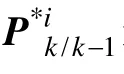
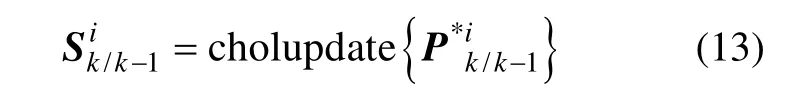
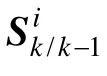
4）量测更新

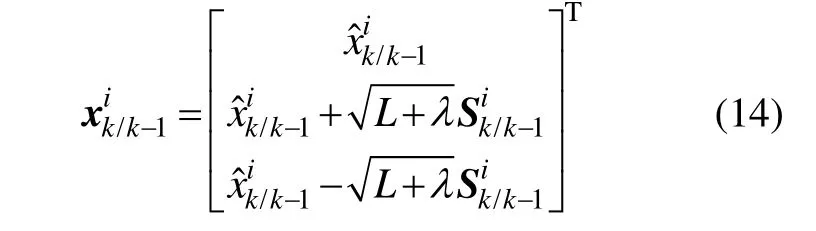
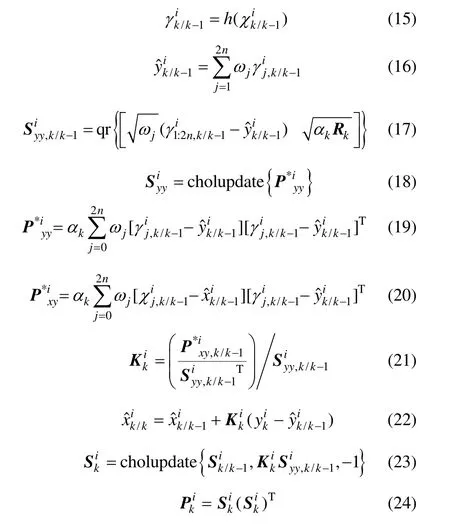
该步骤中使用了线性代数中的 QR分解、Cholesky分解，以协方差平方根阵代替协方差阵参加迭代运算，从而增强状态协方差矩阵更新过程中的数值稳定性，保证了协方差矩阵的非负定性。同时，利用衰减因子 αk调节量测值的权重，减小历史信息对滤波的影响，增强当前量测信息在滤波计算中的作用。

衰减记忆平方根UPF算法利用了以下三种线性代数中的运算技巧，降低了算法的计算复杂度。在此，简单的介绍这三种代数算法：

1） QR分解。协方差矩阵P分解为 P =SST， S可通过QR分解得到，qr{·}表示矩阵的QR分解。

2）Cholesky分解。协方差矩阵P分解为P =SST，S称为P的平方根矩阵。chol{·}表示矩阵P的Cholesky分解，则 S =chol{P}。

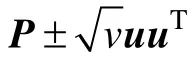
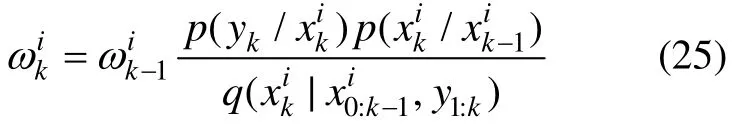
归一化权值

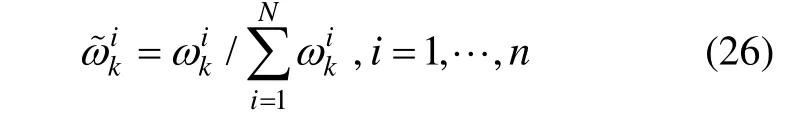
第四步：重采样

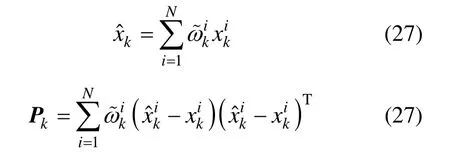
第六步： k = k+1，返回第二步，计算下一时刻的状态估值。

2 仿真实验与分析

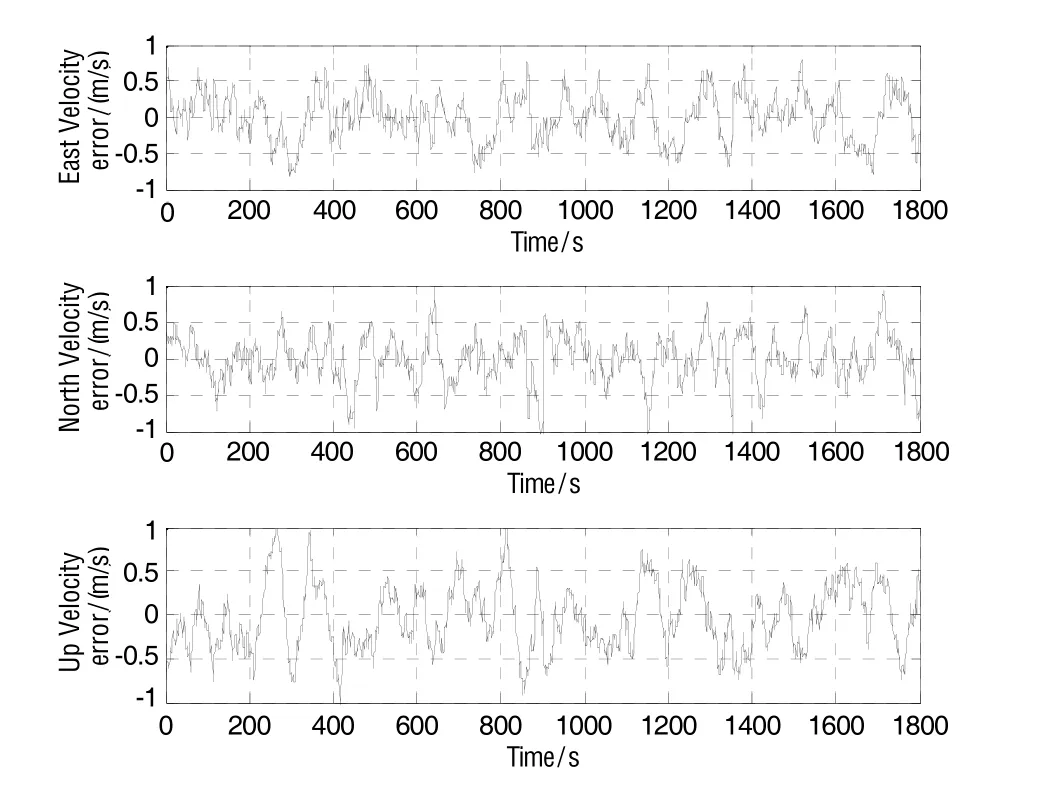
图2 UPF算法速度误差曲线Fig.2 Velocity error of UPF

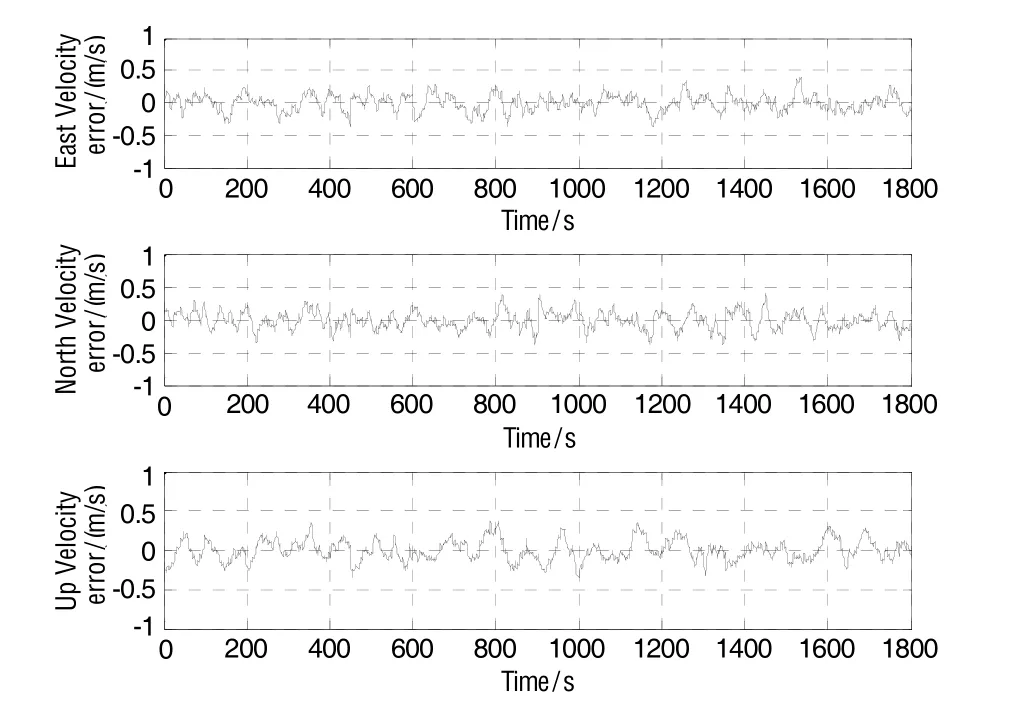
图3 FMSRUPF算法速度误差曲线Fig.3 Velocity error of FMSRUPF

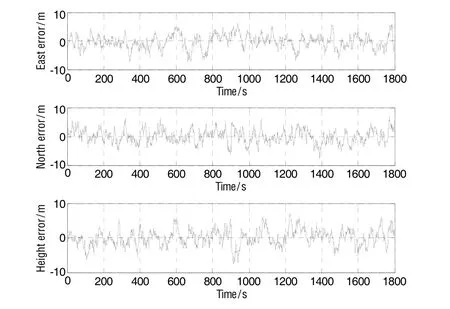
图4 UPF算法位置误差曲线Fig.4 Position error of UPF

图2和图3分别为UPF和FMSRUPF滤波算法对应的速度误差曲线。采用UPF算法计算得到的东向和北向速度误差在(-0.8 m/s, +0.8 m/s)，天向速度误差在(-1 m/s, +1 m/s)；而采用FMSRUPF算法计算得到的东向速度误差在(-0.3 m/s, +0.3 m/s)，北向和天向速度误差在(-0.4 m/s, +0.4 m/s)。图4和图5分别为UPF和FMSRUPF滤波算法对应的位置误差曲线。通过UPF算法计算得到的东向位置误差控制在(-9 m, +9 m)，北向位置误差和高度误差控制在(-8 m, +8 m)；而通过FMSRUPF算法计算得到的东向和北向位置误差控制在(-3 m, +3 m)，高度误差为(-4 m, +4 m)。图6给出了UPF和FMSRUPF算法在50次Monte Carlo仿真实验中的均方根误差曲线，FMSRUPF的均方根误差明显小于UPF的均方根误差。

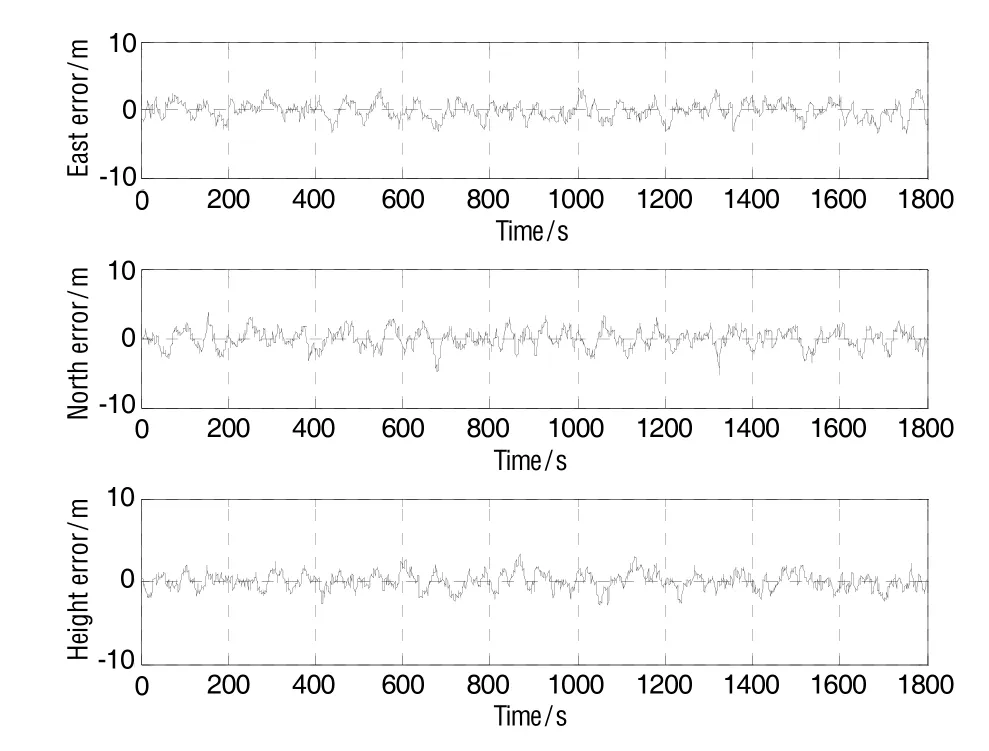
图5 FMSRUPF算法位置误差曲线Fig.5 Position error of FMSRUPF

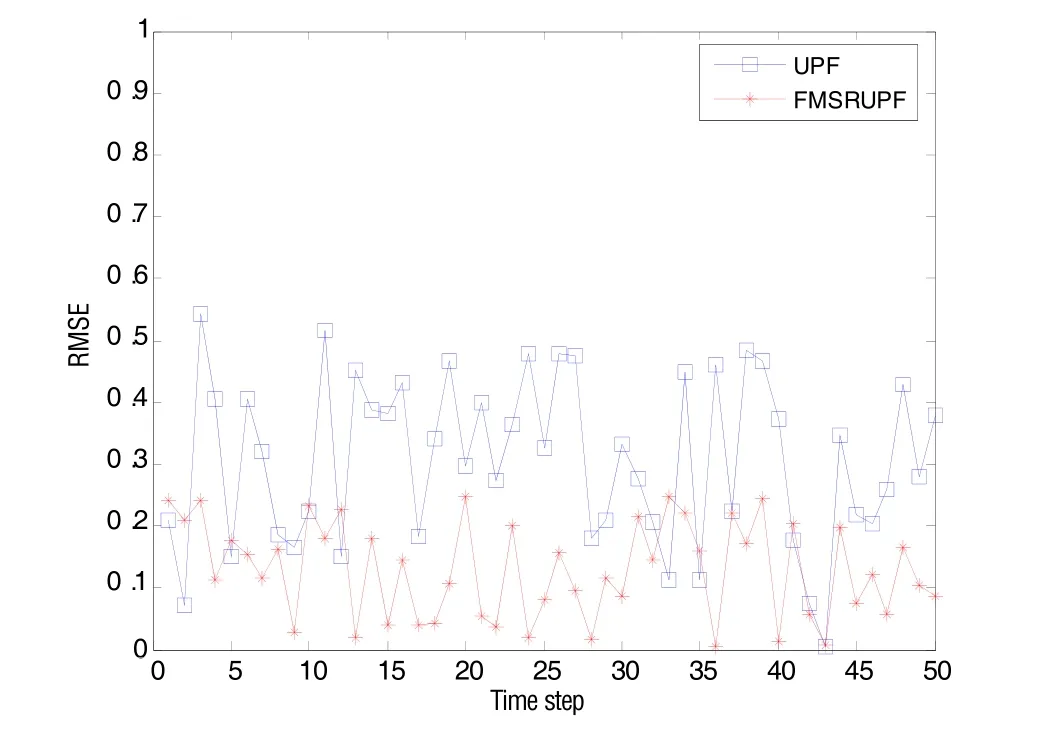
图6 UPF和FMSRUPF的均方根误差曲线Fig.6 Root mean square error curve of UPF and FMSRUPF

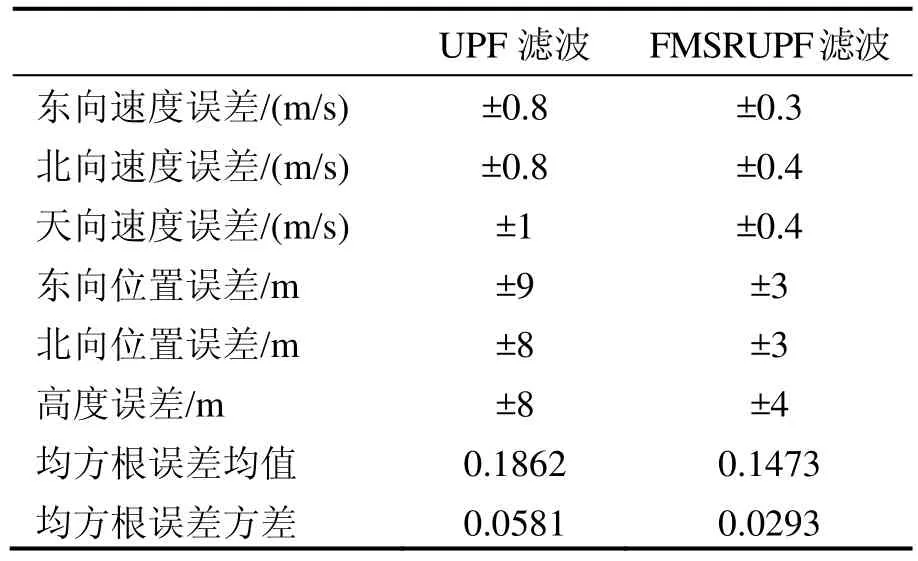
表1 SINS/SAR组合导航系统速度误差及均方根误差比较Tab.1 Comparison of position errors and velocity errors for SINS/SAR integrated navigation system

3 结 论

本文以Unscented粒子滤波为基本框架，吸收了衰减记忆滤波和平方根滤波各自的优点，提出了一种新的衰减记忆平方根UPF算法。该算法利用衰减因子减小历史信息对滤波的影响，增强当前量测信息在滤波计算中的作用；然后，以协方差矩阵的平方根阵代替协方差矩阵进行滤波解算，保证了协方差矩阵的对称性和非负定性，提高了滤波算法数值稳定性和解算精度。仿真实验表明，提出的FMSRUPF算法与UPF算法相比，能有效地改善滤波性能，提高导航滤波精度及稳定性。下一步需要解决的是如何降低计算量的问题。

（References）：

[1] 赵琳，王小旭，丁继成，等. 组合导航系统非线性滤波算法综述[J]. 中国惯性技术学报，2009，17(1)：46-52.

ZHAO Lin, WANG Xiao-xu, DING Ji-cheng, et al. Overview of nonlinear filter methods applied in integrated navigation system[J]. Journal of Chinese Inertial Technology, 2009, 17(1): 46-52.

[2] 王朝辉，徐一兵，许亚伟. 衰减记忆无迹卡尔曼粒子滤波算法研究[J]. 微电子学与计算机，2012，29(8)：50-52.

WANG Chao-hui, XU Yi-bing, XU Ya-wei. Research on memory attenuation UKF particle filter algorithm[J]. Microelectronics & Computer, 2012, 29(8): 50-52.

[3] CHEN Ke-xin, LI Shao-yuan. Unfalsified adaptive PID control with a fading memory cost function[C]//The 33rd Chinese Control Conference. Nanjing, China, 2014, D: 5179-5183.

[4] 董春敏，周伟，曹振坦，等. 平方滤波的优越性分析[J]. 测绘与空间地理信息，2012，35(1)：66-68.

DONG Chun-min, ZHOU Wei, CAO Zhen-tan, et al. The superiority analysis of the square root Kalman filter[J]. Geomatics & Spatial Information Technology, 2012, 35(1): 66-68.

[5] Tang Xiaojun, Yan Jie, Zhang Dudu. Square root sigma point Kalman filtering for spacecraft relative navigation[J]. Acta Astronautica, 2010, 66(5/6): 704-713.

[6] NING Xiaolin, HUANG Panpan. Adaptive points range square-root cubature Kalman filter for Mars approach navigation[C]//The 33rd Chinese Control Conference. Nanjing, China, 2014, A: 903-908.

[7] FU Gui-xia, WANG Hong-jian, LI Cun, LI Juan. Improved square root cubature particle filter based navigation method for UUV[C]//The 32rd Chinese Control Conference. Xi’an, China, 2013: 5095-5100.

[8] LIU Ji, GU Xing-sheng. Improved square-root UKF algorithm for state estimation of nonlinear systems[J]. Journal of Donghua University, 2010, 27(1): 74-80.

[9] Tang Xiaojun, Yan Jie, Zhong Dudu. Square-root sigmapoint Kalman filtering for spacecraft relative navigation [J]. Acta Astronautica, 2009, 66(5): 704-713.

[10] 章飞，周杏鹏，陈小惠. 基于衰减记忆滤波的平方根UKF被动目标跟踪算法[J]. 测控技术，2010，29(4)：22-26.

ZHANG Fei, ZHOU Xing-peng, CHEN Xiao-hui. Square-root UKF passive target tracking algorithm based on memory attenuation filtering[J]. Measurement & Control Technology, 2010, 29(4): 22-26.

[11] Yang Y X, Cui X Q. Adaptively robust filter with multi adaptive factors[J]. Survey Review, 2008, 309(40): 260-270.

[12] GAO She-sheng, XUE Li, WEI Wen-hui. Fading adaptive UPF(Unscented Particle Filtering) algorithm and its application to integrated navigation[J]. Journal of Northwestern Polytechnical University, 2012, 30(1): 27-31.

[13] 赵岩，高社生，杨一，等. 自适应SDV-UPF算法及其在紧组合中的应用[J]. 中国惯性技术学报，2014，22(1)：83-88.

ZHAO Yan, GAO She-sheng, YANG Yi, et al. Adaptive SVD-UPF algorithm and application to tightly-coupled integrated navigation[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 83-88.

[14] Zhong Y, Gao S, Li W. A quaternion-based method for SINS/SAR integrated navigation system[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 514-524.

衰减记忆平方根UPF算法及其在组合导航中的应用

高 怡1，高社生1，吴佳鹏2

Fading-memory square-root unscented particle filter algorithm and its application in integrated navigation system

GAO Yi1, GAO She-sheng1, WU Jia-peng2
(1. Department of Automatics Control, Northwestern Polytechnical University, Xi’an 710072, China; 2. Space star Technology Co., LTD, Beijing 100086, China)

In view that covariance matrix may have asymmetry or negative definite problems in unscented particle filtering, a new unscented particle filtering algorithm is presented based on fading memory and square root. This method uses the fading factor to improve the information utilization of the current measurement and reduce the influence of historical information. In the process of filtering, the square root of the covariance matrix is used in iterative calculation instead of the covariance matrix, to ensure the symmetry and positive definite of covariance matrix and effectively improve the computational efficiency and numerical stability. By applying the proposed algorithm in SINS /SAR integrated navigation system, the simulation results demonstrate that the fading memory square-root UPF algorithm outperforms the UPF ones, and can significantly improving the filter accuracy of the integrated system.

fading factor; square root filter; fading memory filter; unscented particle filter; covariance matrix.

1005-6734(2014)06-0777-05

10.13695/j.cnki.12-1222/o3.2014.06.014

TP301.6

A

2014-07-17；

2014-11-24

国家自然科学基金（61174193）；国家自然科学基金资助（批准号：61174193）；中国航天科技集团公司卫星应用研究院创新基金资助（批准号：2012-1521）

高怡（1978—），女，博士，从事信息工程及控制的研究。E-mail：gaoyi_nwpu@163.com

联 系 人：高社生（1956—），男，教授，博士生导师。E-mail：gshshnpu@163.com