基于LMS与二代小波变换的光纤陀螺去噪算法

（1. 东南大学 仪器科学与工程学院，南京 210096；2. 东南大学 微惯性仪表与先进导航技术教育部重点实验室，南京 210096）

（1. 东南大学 仪器科学与工程学院，南京 210096；2. 东南大学 微惯性仪表与先进导航技术教育部重点实验室，南京 210096）

为了降低光纤陀螺输出中的噪声分量，提出一种基于最小均方法与二代小波变换相结合的去噪方法。首先利用LMS算法进行前端预处理，提高信号的信噪比；然后使用SGWT去噪算法降噪，考虑到SGWT去噪算法易受阈值函数的影响，将模糊与平滑因子引入到传统软阈值法，以缩小估计小波系数和原小波系数两者之间的常值偏差；最后，将本文提出的算法应用于某型光纤陀螺的去噪研究中。实验结果表明，相对于SGWT去噪算法，采用 LMS-SGWT算法处理后，光纤陀螺的信噪比从0.1698 dB提高到2.0521 dB，方位对准误差从0.33°降低到0.13°。

LMS算法；二代小波；小波阈值；信号去噪；光纤陀螺

陀螺是惯性导航设备中最重要的器件，用于测量载体的角速率。在各种类型的陀螺中，光纤陀螺因其具有成本低、精度高等优点，被广泛地应用于惯性导航系统[1]。光纤陀螺是根据 Sagnac干涉原理进行工作，当陀螺绕其光纤环圈平面的垂线旋转时，在环圈中以相反方向输出的两束相干光将产生相位差，通过检测光干涉强度就可以检测出载体角速率[2]。光纤陀螺易受温度、电磁环境等因素的影响，导致其输出中存在漂移[3]，从而影响导航精度。为了降低光纤陀螺输出中的漂移，国内外提出了各种处理光纤陀螺漂移的算法。当前对光纤陀螺漂移的处理主要有两种方法：1）使用最优估计的方法，例如Kalman滤波，对陀螺漂移进行估计[4-5]；2）使用信号去噪方法对陀螺输出进行去噪处理，常用方法有小波去噪[6-7]、LMS自适应滤波[8-9]等。

然而上述方法均存在着缺陷：使用Kalman滤波进行最优估计去噪，需要建立光纤陀螺漂移的精确模型，模型的不准确将会降低估计的精度[4]；小波去噪方法对光纤陀螺进行处理，容易引起小波系数在阈值处不连续，影响信号重构，从而导致去噪精度不高[7]；LMS自适应滤波对光纤陀螺漂移进行处理，其收敛的速度与精度受迭代步长的影响[9]。

针对目前光纤陀螺信号去噪方法存在的不足，本文提出了一种基于 LMS与二代小波变换的光纤陀螺去噪算法。引入LMS算法对信号进行前端预处理，以及将模糊与平滑因子引入到传统软阈值法以改进SGWT去噪算法，这样在整体上提高了去噪效果。最后，将本文提出的算法应用于某型光纤陀螺的去噪研究中。实验结果说明，与目前的算法相比较，该方法提高了光纤陀螺输出的精度，优化了初始对准姿态精度。

本文的论述结构是：第1、2节分别介绍了LMS自适应滤波算法和二代小波变换去噪算法的原理及其优缺点；第3节针对上述两种算法的优缺点和它们之间的联系，提出了LMS-SGWT去噪算法；第4节介绍了LMS-SGWT去噪算法的实验验证过程及其结果。

1 LMS自适应滤波算法

LMS算法是基于最陡下降法的思想，用梯度的估计值来替换梯度的精确值，不断地自动调节自身滤波器的抽头权矢量，最后收敛至维纳解[9]。

LMS自适应滤波算法公式：

图1 LMS算法信号流图Fig.1 Signal flowchart of LMS algorithm

在实际的信号去噪过程中，LMS算法易受噪声信号的干扰将产生参数失调噪声。减小步长 μ( n)可降低LMS算法的失调噪声，提高算法的收敛精度，但是这样会降低算法的收敛速度。因此，LMS自适应滤波算法收敛的速度和精度对步长 μ( n)的要求是相互矛盾的，这种矛盾影响到了算法的去噪性能。

2 二代小波变换去噪算法

2.1 提升算法

二代小波变换是基于提升算法的一种小波变换，提升算法首先使用多项式插补的方法获得信号的高频系数，然后通过某种约束条件获取信号的低频系数[11]。二代小波变换不仅继承了第一代小波变换的特性，而且和第一代小波变换相比较，具有算法结构简单、解算速度快、内存空间占用少等优点。

提升算法的结构分为分解(Split)、预测(Predict)和更新(Update)。

分解：将输入信号 si分为2个部分 si-1和 di-1， si-1称为尺度系数子集，di-1称为小波系数子集。常用的分解方法是根据输入信号 si的奇偶顺序，将输入信号分解为奇序列 di-1与偶序列 si-1，分解过程表示为

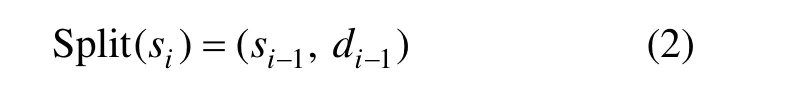
预测：构造预测算子P，用偶序列 si-1的预测值P(si-1)去预测奇序列 di-1，然后用奇序列的实际值di-1与预测值 P(si-1)之差来替换原来的 di-1。

更新：构造更新算子U，使用上述的小波子集di-1对偶序列 si-1进行更新。

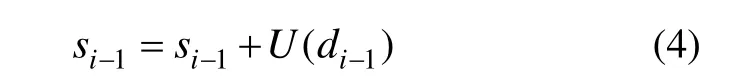
不断重复上述的提升算法，就可以实现对信号的小波变换。提升算法对信号的重构过程与分解过程是互逆的，互换一下预测与更新的顺序，然后再对信号进行合成操作，就能重构信号。

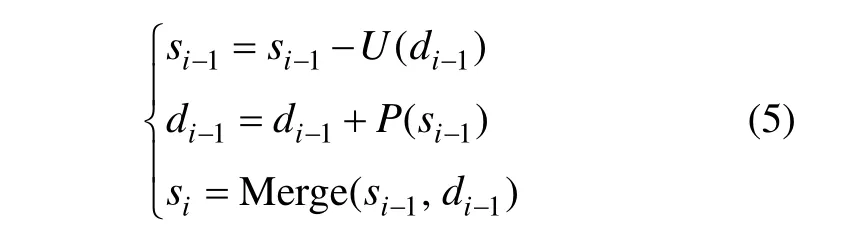
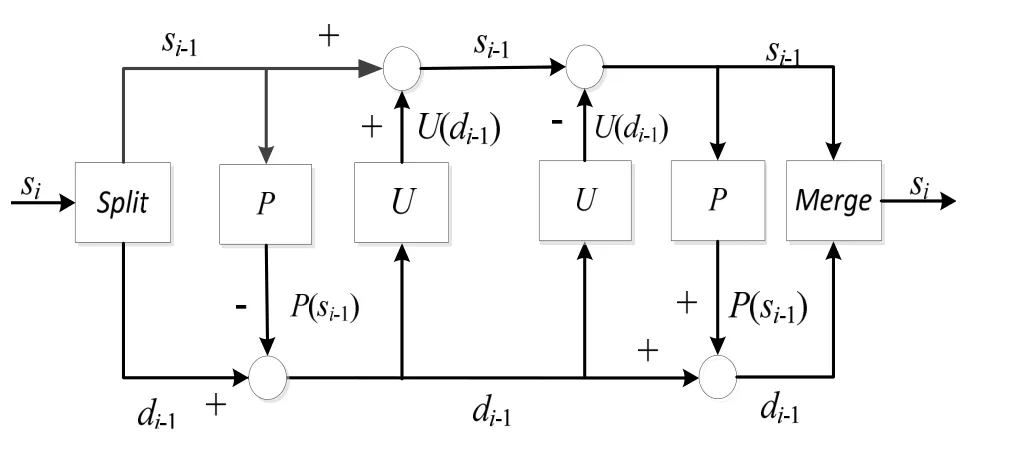
图2 提升算法的分解和重构示意图Fig.2 Decomposition and reconstruction of the lifting scheme

2.2 二代小波变换去噪

在光纤陀螺信号进行二代小波变换(SGWT)后，获得的小波系数主要是由噪声和信号的细节特征组成。根据信号小波系数和噪声小波系数在小波空间内具有不同的分布特性，保留大尺度低分辨率小波系数，同时对各尺度高分辨率小波系数进行“阈值收缩”处理，最后使用二代小波逆变换进行信号重构[7]。

在实际的应用环境中，光纤陀螺易受电磁环境等因素的影响，光纤陀螺输出的信噪比较低。二代小波变换去噪算法对光纤陀螺进行处理时，阈值函数将影响去噪的效果。另外，由于光纤陀螺信号是非平稳信号，在二代小波变换过程中，预测算子与更新算子不能很好地预测或更新信号次数比算子次数高的信号，从而影响到去噪效果[11]，因此单独采用SGWT去噪算法对光纤陀螺信号进行处理，去噪性能有限。

3 LMS-SGWT去噪算法

针对上述讨论的LMS算法与SGWT去噪算法两者的优势与缺陷，本文提出一种LMS-SGWT去噪算法，将LMS算法与SGWT算法进行融合。首先利用LMS算法进行前端平滑预处理，以提高信号的信噪比；然后使用SGWT去噪算法降噪。考虑到SGWT去噪算法易受阈值函数的影响，将模糊与平滑因子引入到传统软阈值法，以缩小估计小波系数和原小波系数两者之间的常值偏差，使重构信号逼近真实信号。

3.1 SGWT模糊自适应小波阈值法

由小波变换与信号的 Lipschitz指数两者之间的关系可知，随着小波变换分解尺度的增大，噪声对应的小波系数的幅值将减小，而有用信号对应的小波系数幅值受分解尺度的影响较小，因此根据每一尺度的小波系数特性，自适应调节小波阈值，实现在保留信号系数的同时最大限度地减小噪声系数的目的[11]。另外，为了缩小估计小波系数和原小波系数两者之间的常值偏差，将模糊因子与Savitzky-Golay平滑算法[12]引入到传统软阈值法。具体步骤如下：

1）信号的二代小波变换处理：采用Db4小波基，小波分解尺度为3层，对光纤陀螺信号进行二代小波变换，得到信号在各尺度上的小波系数。

2） 求解小波阈值：

a) 根据Stein无偏似然估计原理，得到第一尺度上的阈值 λ1：

式中，σ为噪声信号的均方差， d1为第一尺度的小波系数序列， median(d1)为 d1序列的中位数， Wb为风险值对应的小波系数平方。

b) 求解各尺度的小波阈值

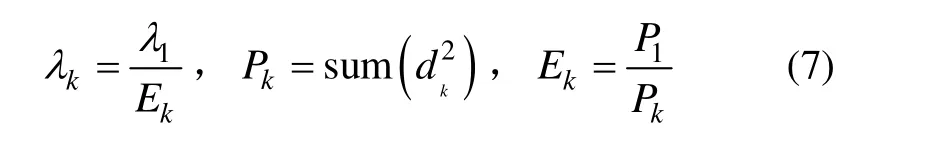
式中： k=1,2,...,l ，l为小波分解尺度；dk为第k层小波系数序列，Pk为第k层小波系数序列的代数平方和。

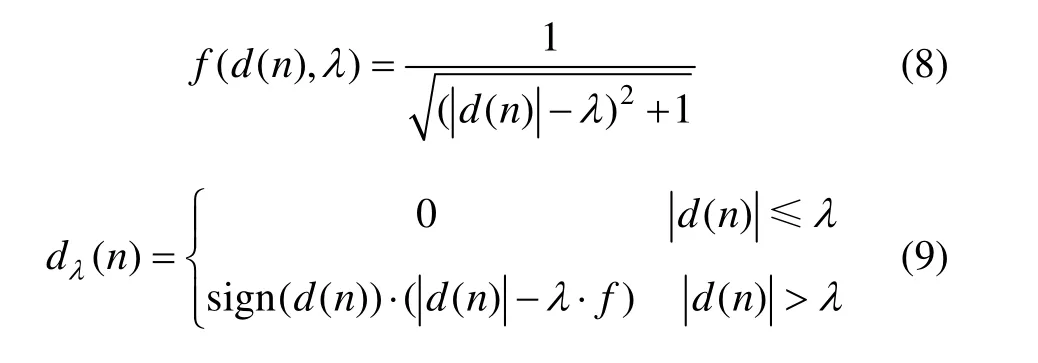
式中，λ为小波阈值，n为时刻点。

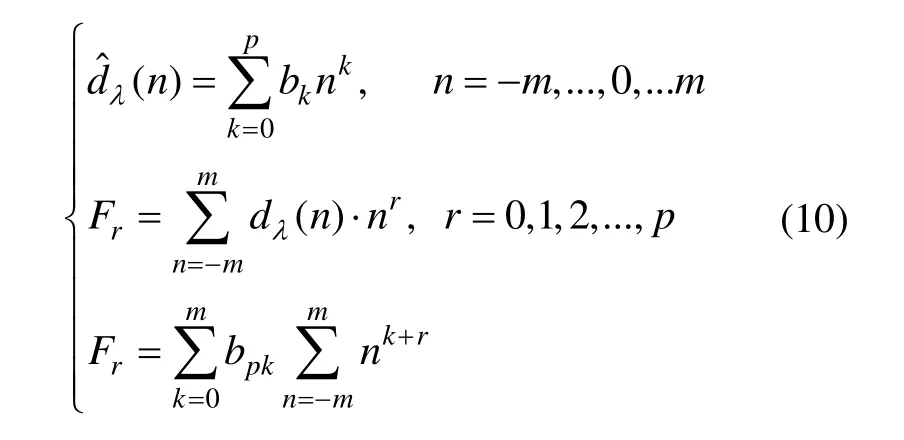
式中：p为多项式阶数，m为平滑窗单边点数；bk拟合系数，可根据式(10)求出。在本文中p取3，m取2。

5） 信号重构：二代小波逆变换作用于各尺度上的尺度系数与估计小波系数。

3.2 LMS-SGWT算法具体步骤

1）LMS算法前端预处理：利用LMS算法预处理光纤陀螺信号。因为在LMS自适应滤波过程中，算法收敛的速度和精度均与迭代步长密切相关，而在本文提出的算法中，因为有SGWT去噪算法的进一步降噪，所以LMS算法的迭代步长主要考虑收敛速度。综合考虑，本文提出一种改进步长公式：

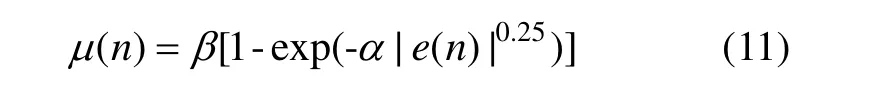
式中，α 为衰减系数，β 为加权系数。α 与β 通过多次实验测得：α 为30.05，β 为25.5。

2） 二代小波变换信号去噪：针对步骤1）处理后的光纤陀螺信号，采用SGWT模糊自适应小波阈值法进行去噪处理。

4 光纤陀螺信号去噪实验及分析

4.1 光纤陀螺信号去噪实验

将IMU组件固定在水平静止的三轴转台上，转台的内框和中框为0°，外框角度为45°。当光纤陀螺开机稳定后，对IMU的输出信号进行采样，采样频率是200 Hz，采样时间长度是300 s。使用文献[7]中的SGWT去噪算法、本文提出的SGWT模糊自适应阈值去噪算法以及LMS-SGWT去噪算法，对光纤陀螺信号分别进行去噪处理。图4和表1给出了去噪实验结果（以 Z轴陀螺信号为例）。

图3 惯性组件和三轴转台图Fig.3 IMU and three-axle table

由图4和表1可知，FOG原始信号的标准差为0.011 (°)/s，信噪比为0.1698 dB，标准差大，信噪比低，说明原始信号中含有大量噪声。经算法降噪处理以后，信号的标准差减小，信噪比提高。例如，经SGWT算法去噪，信号的标准差降低到0.0095 (°)/s，信噪比提高到0.3144 dB，说明上述算法都具有降噪功能，但是各种去噪信号的标准差和信噪比各不相同，说明算法性能存在差异。FOG信号经SGWT改进算法处理后，信噪比提高到0.4925 dB，优于SGWT算法的0.3144 dB，可知本文提出的SGWT改进算法性能优于文献[7]中的 SGWT算法。信号经 LMSSGWT算法处理后，信号的信噪比为2.0521 dB，改善最大，说明LMS-SGWT去噪算法具有明显的优势。

图4b SGWT算法去噪信号时域图 Fig.4 b Time-domain diagram of SGWT denoising signal

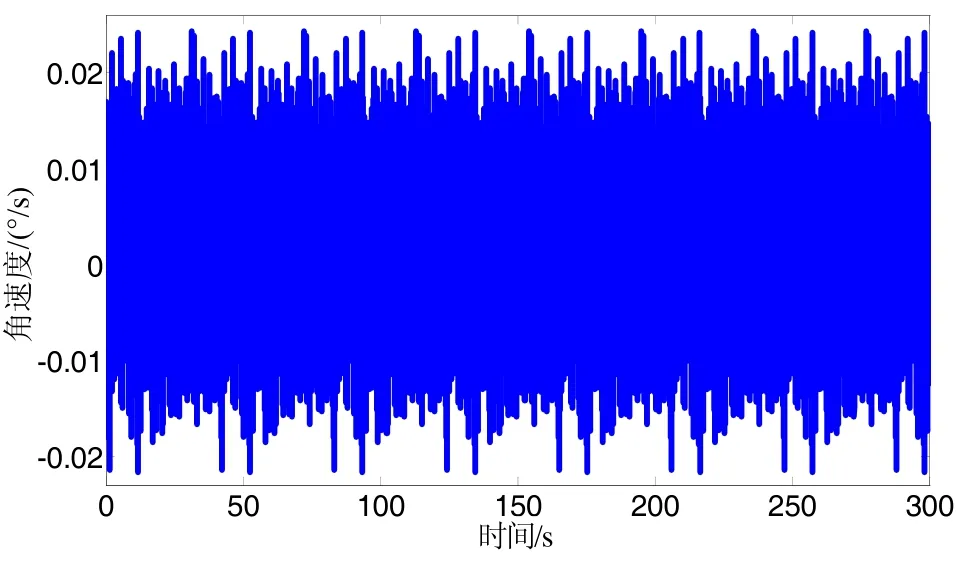
图4 c SGWT改进算法去噪信号时域图Fig.4 c Time-domain diagram of improved SGWT denoising signal

图4d LMS-SGWT算法去噪信号时域图Fig.4 d Time-domain diagram of LMS-SGWT denoising signal

4.2 粗对准姿态误差实验

在捷联惯性导航中，初始对准的姿态精度受光纤陀螺精度的影响，在相同实验条件与算法下，初始对准姿态精度可以反映光纤陀螺的精度。因此，为了进一步对比分析各种去噪算法的效果，设计了以下捷联惯性导航解析粗对准实验。将IMU组件固定在水平静止的三轴转台上，转台内框和中框角度为0°，外框角度为45°，IMU输出信号的采样频率为200 Hz。在对准实验前，使用文献[7]中的SGWT算法，本文提出的SGWT改进算法以及LMS-SGWT算法对光纤陀螺信号分别进行去噪处理。利用FOG原始信号与去噪信号分别进行对准实验，在第150 s计算姿态角。实验结果如图5所示(以航向角误差为例)。

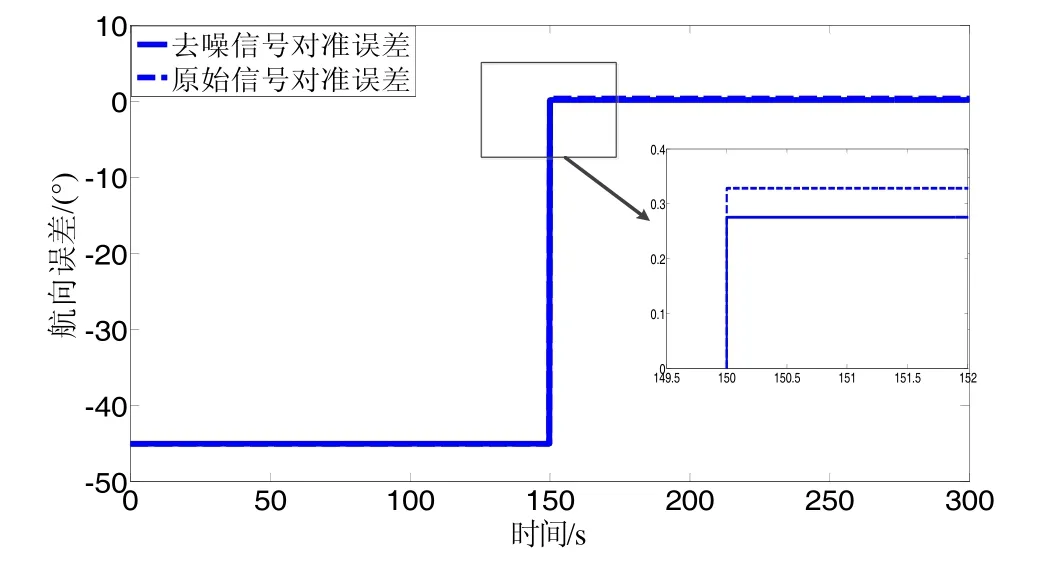
图5 a SGWT算法去噪信号航向误差Fig.5 a Heading error of SGWT denoising signal

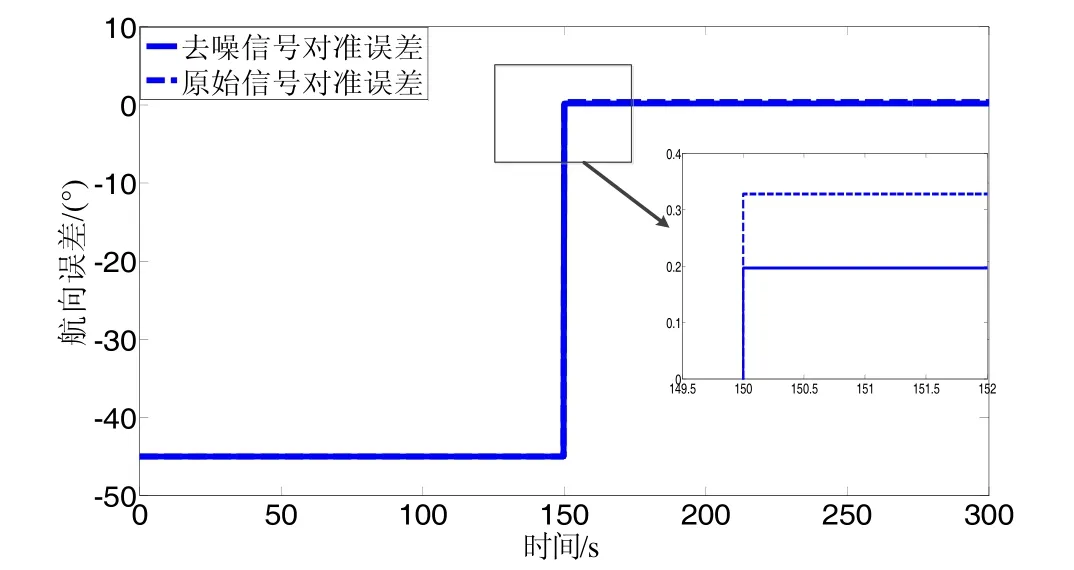
图5 b SGWT改进算法去噪信号航向误差Fig.5 b Heading error of improved SGWT denoising signal

图5 c LMS-SGWT算法去噪信号航向误差Fig.5 c Heading error of LMS-SGWT denoising signal

由图5可知，与原始信号相比，使用上述三种去噪信号进行对准实验，航向角误差不同程度地都降低了，间接说明上述去噪算法能对光纤陀螺信号去噪。由图5(b)与图5(a)对比可知，在FOG信号经SGWT改进算法去噪后，粗对准的航向角误差为 0.21°，优于图5(a)中的0.28°，说明SGWT改进算法的去噪性能比文献[7]中的SGWT算法更好。使用LMS-SGWT算法去噪后的信号进行粗对准，航向角误差为0.13°，其误差最小，说明在上述三种去噪算法中，LMS-SGWT算法的去噪效果最好。

5 结 论

为了降低光纤陀螺输出中的噪声分量，本文提出了基于 LMS与二代小波变换的光纤陀螺信号去噪算法。该算法首先利用LMS算法进行前端预处理，以提高信号的信噪比，然后使用SGWT模糊自适应小波阈值法降噪。利用某型光纤陀螺的输出信号验证算法的性能，实验结果表明，本文提出的LMS-SGWT算法的效果优于其它算法，并且优化了捷联惯性导航初始对准姿态精度。由于LMS-SGWT算法结构简单，占用内存空间少，所以在工程应用中有一定的参考价值。

（

）

[1] Strandjord L K, Qiu Tiequn, Wun Jianfeng, et al. Resonator fiber optic gyro progress including observation of navigation grade angle random walk[J]. SPIE Proceedings, 2012, 8421(9): 1-5.

[2] 霍炬，王石静，杨明，马战国. 基于小波变换阈值法处理光纤陀螺信号噪声[J]. 中国惯性技术学报，2008，16(3)：343-347.

HUO Ju, WANG Shi-jing, YANG Ming, MA Zhan-guo. Noise processing of FOG signal based on wavelet threshold value[J]. Journal of Chinese Inertial Technology, 2008, 16(3): 343-347.

[3] Blin S, Dignonet M J F, Kino G S. Noise analysis of an air-core fiber optic gyroscope[J]. IEEE Photonics Technology Letters, 2007, 19(19): 1520-1522.

[4] Peesapati R, Sabat S L, Karthik K P, et al. Efficient hybrid Kalman filter for denoising fiber optic gyroscope signal[J]. Journal of Optik, 2013, 124: 4549-4556.

[5] Li Xuyou, He Zhou, Zhang Chen, et al. Application of adaptive filtering to digital closed-loop fiber optic gyroscope[C]//International Conference on Mechatronics and Automation. 2009: 443-447.

[6] 申冲，陈熙源. 基于小波包变换与前向线性预测滤波的光纤陀螺去噪算法[J]. 东南大学学报，2011，41(5)：977-981.

SHEN Chong, CHEN Xi-yuan. Denoising algorithm for FOG based on wavelet packet transform and FLP algorithm[J]. Journal of Southeast University, 2011, 41(5): 977-981.

[7] 高伟，祖悦，王伟，等. 基于二代小波的光纤陀螺实时降噪方法研究[J]. 仪器仪表学报，2012，33(4)：774-780.

GAO Wei, ZU Yue, WANG Wei, et al. Research on real-time de-noising of FOG based on second generation wavelet transform[J]. Chinese Journal of Scientific Instrument, 2011, 33(4): 774-780.

[8] Hu Kaibo, Liu Yaxuan. Adaptive noise cancella- tion method for fiber optic gyroscope[J]. Procedia Engineering, 2011, 29: 1338-1343.

[9] 陈世同，孙枫，高伟，等. 基于归一化LMS算法的光纤陀螺降噪技术研究[J]. 仪器仪表学报，2009，30(3)：521-525.

CHEN Shi-tong, SUN Feng, GAO Wei, et al. Research on the noise control technology in FOG based on NLMS algorithm[J]. Chinese Journal of Scientific Instrument, 2009, 30(3):521-525.

[10] 李明，杨成梧. 基于模糊推理的变步长自适应滤波算法[J]. 控制工程，2006，13(3)：237-239.

LI Ming, YANG Cheng-wu. Variable step size LMS adaptive filtering algorithm based on fuzzy inference[J]. Control Engineering of China, 2006, 13(3): 237-239.

[11] Song Xiaodi, Zhou Chengke, Hepburn D M, et al. Second generation wavelet transform for data denoising in PD measurement[C]. IEEE Transactions on Dielectrics and Electrical Insulation, 2007, 14(6): 1531-1537.

[12] Candan C, Inan H. A unified framework for derivation and implementation of Savitzky–Golay filters[J]. Signal Processing, 2014, 104: 203-211.

基于LMS与二代小波变换的光纤陀螺去噪算法

徐晓苏1,2，吴 亮1,2，刘义亭1,2

Denoising algorithm for FOG based on LMS and second-generation wavelet transform

XU Xiao-su1,2, WU Liang1,2, LIU Yi-ting1,2
(1. School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China; 2. Key Laboratory of Micro-inertial Instrument and Advanced Navigation Technology, Southeast University, Nanjing 210096, China)

To denoise the FOG output signal, a denoising algorithm based on LMS (Least Mean Square) and the Second Generation Wavelet Transform (SGWT) is proposed. Firstly, the LMS algorithm is used to pretreat and improve the signal’s signal-noise ratio (SNR). Then the SGWT algorithm is used to further denoise the signal. Considering that the SGWT algorithm is easily influenced by threshold function, a fuzzy factor and a smooth factor are introduced to reduce the constant deviation between estimated wavelet coefficient and original wavelet coefficient. A certain kind of FOG is used to verify the LMS-SGWT algorithm. Experiment results show that the SNR of FOG is increased from 0.1698 dB to 2.0521dB, and the alignment error of heading is decreased from 0.33° to 0.13°.

LMS algorithm; second generation wavelet; wavelet threshold; signal de-noising; FOG

1005-6734(2014)06-0810-05

10.13695/j.cnki.12-1222/o3.2014.06.020

U666.1

A

2014-07-17；

2014-10-27

国家自然科学基金项目（51175082，60874092）

徐晓苏（1961—），男，教授，博士生导师，从事惯性技术与应用研究。E-mail：xxs@seu.edu.cn