基于CWPA模型的最优平滑算法性能及其应用

（1. 哈尔滨工程大学 自动化学院，哈尔滨 150001；2. 魁北克大学 ETS学院，蒙特利尔 H3C 1K3，加拿大）

（1. 哈尔滨工程大学 自动化学院，哈尔滨 150001；2. 魁北克大学 ETS学院，蒙特利尔 H3C 1K3，加拿大）

针对线性高斯系统的平滑问题，分析了RTS固定区间平滑与双滤波器固定区间平滑两种算法，提出了一种滤波存储数据更少的RTS平滑新算法。结合平面内的运动追踪问题，基于二维CWPA模型，仿真分析了卡尔曼滤波、RTS固定区间平滑以及双滤波器平滑算法的估计性能。仿真结果表明，两种固定区间平滑算法的估计效果等效，精度均优于卡尔曼滤波，对于实际问题中固定区间平滑算法的选用具有一定的参考价值。最后，结合双滤波器结构提出了一种基于双平滑器的舰载武器惯导传递对准精度评估方法，结果表明新方法相比于单一的平滑算法，可以获取更优的综合平滑性能，特别提升了水平姿态对准误差的平滑估计性能。

最优平滑；卡尔曼滤波；RTS平滑器；双滤波器平滑器；CWPA模型；传递对准精度评估

最优估计是指从受噪声影响的量测量中估计出所需的状态量，且使性能指标达到特定条件下的最优[1]。由于最优估计理论不仅能获取状态的估计值，往往还可以同时获取能够表征状态估计性能的指标量，在自动控制、信号处理、通讯、图像处理、导航、测绘、石油勘探和金融等诸多领域中，均得到了极为广泛的应用[2]。

在已知一个时间段内量测信息的条件下，依据待估计状态与该时间段所属时间的关系，可将最优估计问题分为三类：预测、滤波和平滑。滤波估计具有良好的实时性，能够满足绝大多数的应用要求，因此得到了最为广泛的研究与发展。对于平滑估计，在一定程度上属于基于滤波估计的数据再处理算法，其较高的解算复杂程度和实时性的不足，限制了平滑的应用范围[3]。

最优平滑算法可分为固定区间平滑、固定点平滑和固定滞后平滑三类[4]。固定区间平滑算法可以利用在固定的时间区间内得到的所有量测值，去估计该时间区间内某一时刻的状态值。它往往可以获得比固定点平滑和固定滞后平滑较高估计精度，因此在对参数估计精度要求较高的惯性导航领域得到了较多的应用。例如，文献[5]利用RTS固定区间平滑算法评估了舰载武器惯导系统传递对准的性能，获得了比固定点平滑更优的效果。文献[6]利用RTS固定区间平滑算法有效实现了陀螺漂移模型的参数辨识，且表明固定区间平滑算法比卡尔曼滤波方法的估计精度更高。文献[7]将 RTS固定区间平滑算法应用于实际飞行状态的实时估计中。文献[8]将固定区间平滑算法应用到了GPS/INS组合导航系统中，采用事后处理的方法，获得了较好的定位精度。但现有文献多为单一的RTS固定区间平滑算法的应用型研究，并没有针对另一种国外常用的双滤波器固定区间平滑算法或者上述两种算法的性能进行实质性的分析，尤其缺少组合平滑方法方面的分析及应用研究。

本文结合线性状态空间系统模型，依次分析了最为常用的 RTS平滑算法和双滤波器平滑算法。针对RTS平滑算法中存在数据存储量大的问题，提出了改进的 RTS平滑算法，并结合连续维纳加速(Continue Wiener Process Acceleration，CWPA)数学模型，通过仿真分析了两种平滑算法在噪声驱动状态估计问题中的性能。最后，设计了一种基于双滤波器结构的舰载武器惯导传递对准精度评估方法，提高了评估系统的性能，特别是水平姿态误差的平滑精度。

1 高斯线性模型与卡尔曼滤波

1.1 状态空间模型

在现代控制理论中，通常将离散化后的线性系统表示为如下状态空间模型形式：

式中：Φk,k-1为一步转移阵， Hk为量测阵，Wk-1、Vk分别为系统噪声、量测噪声。

当系统噪声与量测噪声均设置为高斯白噪声时，该线性系统同时具备高斯及线性特性。

1.2 经典卡尔曼滤波

基于系统高斯线性假设，Kalman于1960年提出了经典的线性滤波方法[9]。滤波方法可表示为：

① 基于系统状态模型的一步预测，并给出表征一步预测性能的协方差阵：

2 RTS固定区间平滑算法

在Kalman及Bucy建立经典最优线性滤波方法理论体系后，Rauch、Tung和Striebelrts于1965年提出了经典的固定区间平滑算法，因此也称为RTS固定区间平滑算法[10]。

文献[11]在贝叶斯意义下，将RTS固定区间的平滑问题用条件概率分布表示为

结合条件概率密度公式，相邻时刻状态的联合概率密度可表示为

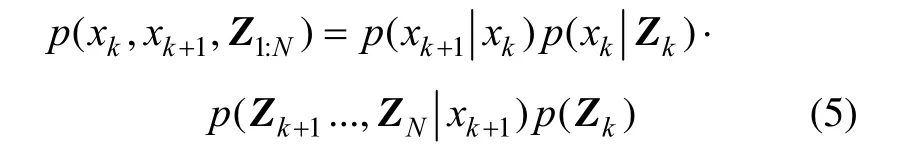
基于高斯假设条件，利用极大似然估计准则，可推导出RTS平滑算法的表达为

由式(6)可知，RTS固定区间平滑有以下特性：

① 平滑解算过程相对于滤波过程是逆向的。因此，RTS固定区间平滑算法在传递对准精度评估等侧重于初始状态获取的应用中，最终平滑值的读取方式与普通前向滤波器估计值的读取方式相反。

② 平滑过程利用了前向滤波过程中所产生的数据。因此，平滑解算需要在滤波过程中实时存储数据，所存储的数据为 4个矩阵，分别为估计值、一步转移阵估计的均方差阵，以及一步预测均方差阵

RTS平滑算法的解算流程图，如图1所示。

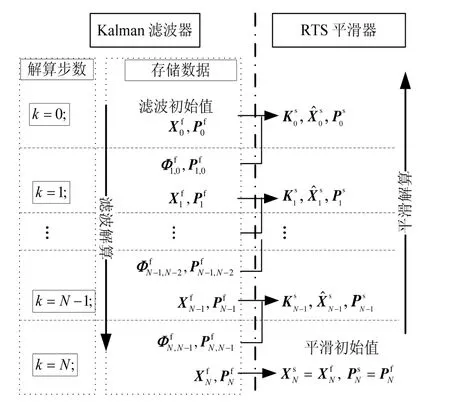
图1 RTS平滑算法解算流程图Fig.1 Calculation flowchart of RTS smoother

图 2 改进型RTS平滑算法解算流程图Fig.2 Calculation flowchart of advanced RTS smoother

3 双滤波器固定区间平滑

双滤波器固定区间平滑(Two-Filter Smoother, TFS)，也被称为前向-后向滤波器。其滤波结构由前向滤波器、后向滤波器以及数据融合三部分组成[12]。

前向滤波器在线性高斯估计问题中，等同于 1.2节中所论述的标准卡尔曼滤波器。后向滤波器则用于提供后向虚拟轨迹和后向量测更新[13]。

后向滤波方程的表示形式与前向滤波非常相似，但是后向滤波过程中的时间更新相对于实际时间是逆序过程。假设量测量所在的固定时间区间为[0,N]，记前向滤波步数为k，后向滤波步数为τ，则有τ= N-k ， τ= N,N -1,…, 0。

基于相同状态空间模型以及时间逆序，可得后向滤波器的解算表达式为：

式中，上标“b”表示后向滤波。TFS固定区间平滑中还包含了信息融合过程，其表达式为：

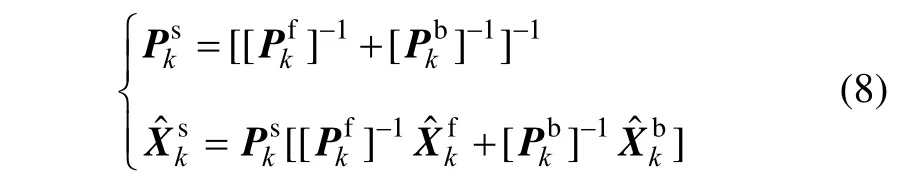
图 3 TFS平滑算法解算流程图Fig.3 Calculation flowchart of TFS smoother

图3给出了双滤波器平滑的结构示意图。为了保证后向滤波器解算的独立性，需要避免将前向滤波的结果提供给后向滤波器。因此，对于虚拟的后向滤波过程，其后向滤波初值及后向滤波协方差阵很难精确获取，这在很大程度上限制了TFS平滑算法的应用。而惯导系统属于推算导航系统，TFS的后向滤波解算可以通过外部提供最终导航状态进行逆向解算较为容易地实现[14]。因此，TFS在惯导领域具有特别的适用性。

4 两种固定区间平滑算法性能分析

4.1 性能分析方法

针对上述两种基本固定区间平滑算法，本文引入了CWPA模型，展开了基于CWPA模型的平滑算法性能分析研究。该模型被应用于平面内运动体的位置跟踪问题，具体问题可描述为：运动体在坐标确定的二维平面内运动，有一受高斯白噪声影响的定位传感器，通过该传感器测量运动体坐标以实现定位，并期望同时获取运动体的速度及加速度信息[15]。由于该模型与简化后的二维平面惯导模型十分相似，因此它对于通常忽略天向通道的舰船领域惯导研究具有较强的适用性。

本节利用较为简单的CWPA模型，对拟应用于舰船领域惯导的平滑算法进行研究，为后续平滑算法的具体工程应用提供依据。

研究过程中具体的实施方法为：1）由轨迹发生器模拟产生真实的连续运动轨迹以及噪声污染的离散量测信息；2）结合CWPA模型，利用卡尔曼滤波、RTS及TFS算法分别估计出运动体的位置与速度，并同时输出估计值的均方根误差；3）通过轨迹与均方根误差研究各算法的性能：估计轨迹、估计速度曲线越接近真实轨迹，均方根误差越小，表明算法性能越优。

特别要注意的是，平面坐标进行了标准单位化，并将估计得到的每一步离散运动体位置、速度信息进行了汇总，标识了起始点。此外，本文主要针对适用于离线处理的潜在应用进行研究，不对算法的实时性进行分析。

4.2 二维CWPA模型

对运动体的位置跟踪问题进行数学描述，状态变量为

式中：xk、yk分别表示运动体位置的横、纵坐标；、分别表示运动体速度在横、纵坐标的投影；、分别表示运动加速度在横、纵坐标的投影。

运动体的追踪问题可用线性时变模型表示为：

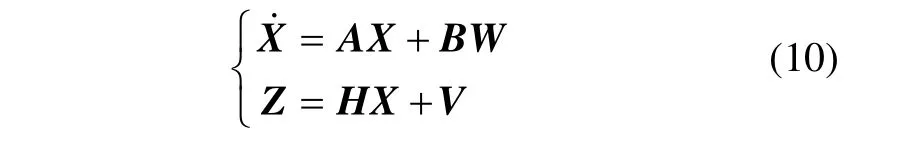
由于所述的卡尔曼滤波及两种固定区间平滑算法均基于离散系统模型，因此需用泰勒级数展开法将式(10)离散化，记离散化相关时间为 Δt，则有：

系统噪声矩阵为：

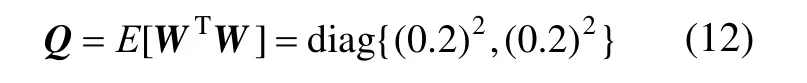
其量测噪声矩阵为：

初始速度及加速度均设置为0，仿真进行50步。由系统随机产生一组真实运动轨迹及其量测轨迹，如图4所示，图中细实线表示运动体真实的运动轨迹，离散点表示传感器测得的量测量，圆圈处表示轨迹初始点，起始点的位置坐标为(0,0)。由图4可知，由于传感器存在量测噪声，直接测量结果并不能很好地反应真实轨迹。

4.3 仿真结果

针对基于二维CWPA模型的运动追踪估计问题，分别利用标准离散卡尔曼滤波、RTS平滑算法以及TFS平滑算法进行仿真分析。

首先，利用卡尔曼滤波(Kalman Filter, KF)进行仿真，获取实时位置与速度滤波估计值。所得的滤波估计轨迹，如图5所示。图中，虚线表示真实的运动轨迹与速度，实线表示KF估计得到的轨迹与速度，圆圈所示为运动起始点，位置坐标为(0,0)；速度以二维向量的形式标识，格式为(x′,y′)，初始速度为(0,0)。

图 4 真实运动轨迹及其量测量Fig.4 Real trajectory and measurements of moving object

由图5可知，对于运动轨迹，KF估计得到的轨迹较为理想；但KF估计得到的速度与真实速度存在较大误差。

图 5 真实运动参数与卡尔曼滤波估计结果对比Fig.5 The real motion parameters and estimates by KF

利用RTS算法估计得到的平滑结果，如图6所示，图中虚线表示真实的运动轨迹与速度，实线表示RTS算法估计得到的轨迹与速度。

图 6 真实运动参数与RTS平滑估计值对比Fig.6 Real motion parameters and estimates by RTS smoother

由图6可知，对于运动轨迹，利用RTS平滑算法估计得到的轨迹，与真实轨迹几乎重合；但RTS平滑算法估计得到的速度曲线更加平滑，数据稳定性增强了，与真实速度误差较小，估计效果要优于卡尔曼滤波结果。利用TFS平滑算法估计得到的平滑结果，如图7所示。

结合图6、图7可知，RTS和TFS固定区间平滑的估计效果几乎一致，均能较好的跟踪真实轨迹，得到的速度估计曲线也较为平滑。

三种估计方法的位置估值均方误差，如表1所示。三种估计方法的速度估值均方误差，如表2所示。

由仿真图及均方误差表可知，RTS与TFS这两种平滑算法的估计性能均优于KF。这主要是由于两种平滑算法都充分利用了平滑前滤波过程所产生的数据，提高了估计精度。而由RTS 与TFS这两种固定区间平滑算法得到的估计结果曲线及各估计值的均方误差均一致，表明这两种平滑算法的估计效果是等效的。

图 7 真实运动参数与TFS平滑估计值对比Fig.7 Real motion parameters and estimates by TFS smoother

表 1 三种估计方法位置估计值的均方误差Tab.1 Errors of position estimates for the three algorithms

表 2 三种估计方法速度估计值的均方误差Tab.2 Errors of velocity estimates for the three algorithms

上述结论对于平滑算法的应用具有重要的实际意义。一方面，由于RTS平滑算法在平滑值解算时，需要进行一步转移协方差阵的求逆，这有可能导致误差协方差阵失去正定性，从而导致平滑结果失效，此时，可以用TFS平滑算法替代，因为TFS仅在数据融合时进行了滤波协方差阵求逆运算；另一方面，TFS平滑算法对于后向滤波有着较高的要求，如果应用信息滤波或者虚拟后向滤波方法无法获取理想效果，可以利用 RTS平滑算法替代，而且两种算法具有同等的估计性能。

5 基于双滤波器结构的双平滑器精度评估方法

舰载武器惯导系统传递对准的精度评估是最优平滑算法较为常见的应用之一。在舰载武器惯导系统完成传递对准后，立即转入评估过程，基于传递对准误差在导航信息中传播的特性，利用舰载武器惯导相对外部精确信息基准的误差量测，结合RTS平滑、固定点平滑(Fixed Point Smoother, FPS)[12]等最优平滑算法，对对准结束时刻的对准误差进行平滑估计。

但现有的对准精度评估研究，存有两个明显特征：

① 所研究的内容侧重于评估方案的改进。文献[16]论述了平滑估计方案相对于光学物理检测手段的优势，确立进行性能评估的经典方法。而文献[3][5]均提出引入高精度航向基准信息对提升方位对准误差评估性能的重要性，并解决外部基准信息引入所带来的问题，则属于对估计器匹配方法的改进、优选。

② 所应用的平滑算法较为单一。一方面，算法的选用范畴仍然局限于经典的RTS或FPS平滑算法；另一方面，算法使用时只选用单种平滑算法。

针对上述问题，本文结合对平滑算法的性能研究，基于双滤波器结构提出一种新的双平滑器传递对准精度评估方法。双平滑器平滑(Two-Smoother Smoothing，TSS)中涉及的前向估计器选用FPS算法，后向估计器选用RTS平滑算法。该方法的解算流程如图8所示。

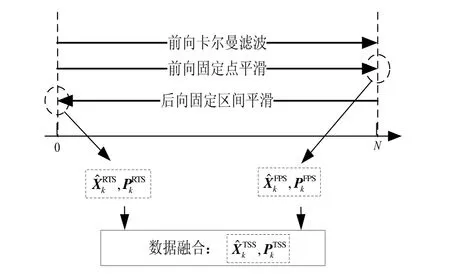
图 8 基于TSS算法的精度评估方法示意图Fig.8 Evaluation scheme based on two-smoother smoothing

该方法的前向平滑中，FPS解算过程相对于 KF解算过程独立；后向平滑中，RTS平滑基于经典KF，并呈后向解算的算法特性。因此，所设计的TSS算法能够保证前向、后向平滑解算过程的独立性。

通过对式(8)进行转换，可得：

式(14)表明：TSS算法对全部状态量的综合估计性能要优于采用单一的前向FPS或后向RTS算法。

针对对准精度评估中最为关注的对准姿态误差，表3给出了FPS、RTS及TSS算法在对准精度评估中水平姿态误差估计值的均方误差。

由表3可知，所提出的TSS算法水平姿态对准误差估计值的均方误差，要优于FPS及RTS。但必须指出，由于FPS算法的数据稳定性较差，重复仿真中会出现多次偏差明显很大的估计值，应予以剔除。否则所得到FPS的水平姿态估计值均方误差将过大，间接影响后续的数据融合以及对TSS算法的评价结果。因此，表3中FPS的均方误差值稍优于RTS。此外，鉴于FPS算法对方位姿态对准误差的估计数据稳定性较差，且受不同评估方案影响很大，表3中未对方位姿态对准误差进行分析。

表3 三种平滑方法水平姿态对准误差估计值的均方误差Tab.3 Errors of horizontal misalignment estimates for the three smoothing algorithms

基于双滤波器结构的平滑算法还可以作为平滑算法框架，针对前向平滑算法或后向平滑算法进行优化(例如对前向FPS的平滑数据稳定性进行改进)，甚至扩展至非线性平滑领域。对于一些静态应用对象，还可以作为估计算法框架，有针对性地对前向估计器及后向估计器进行优选，例如：引入 UKF、PF等非线性滤波器[17]，设计出最适用于该对象的估计算法。

6 结 论

综上所述，本文得到下述结论：所提出的改进型RTS固定区间平滑算法，可以减少其滤波过程所存储的数据，进而提升RTS平滑算法的计算效率。仿真结果表明：RTS固定区间平滑算法与TFS平滑算法的估计性能具有等效性，可以获取同等精度的轨迹、速度估计结果；所提出的基于双滤波结构的舰载武器惯导传递对准精度评估方法，可以获取较传统单一FPS或RTS算法更优的平滑性能。最后，展望了基于该算法框架的后续研究方向。

（References）：

[1] 秦永元，张洪钺，汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安：西北工业大学出版社，1998：5-7, 16-20, 34.

[2] Arthur G. Applied optimal estimation[M]. The MIT Press, 1974: 1-5.

[3] 程建华，陈岱岱，田军. 基于分类因子自适应滤波的惯导传递对准精度评估方法[J]. 中国惯性技术学报，2013，21(5)：598-603.

Cheng J H, Chen D D, Tian J. Transfer alignment accuracy evaluation for SINS based on classified factors adaptive filter[J]. Journal of Chinese Inertial Technology, 2013, 21(5): 598-603.

[4] 史忠科. 最优估计的计算方法[M]. 北京：科学出版社，2001：36-37.

[5] 程建华，陈岱岱. 舰船姿态辅助DGPS的传递对准精度评估方法[J]. 哈尔滨工程大学学报，2012，33(12)：1509-1514.

CHENG Jian-hua, CHEN Dai-dai. Transfer alignment accuracy evaluation based on DGPS assisted with the ship attitudes[J]. Journal of Harbin Engineering University, 2012, 33(12): 1509-1514.

[6] Nash R A, Kasper J F, Crawford B, et al. Application of optimal smoothing to the testing and evaluation of inertial navigation systems and components[J]. IEEE Transactions on Automatic Control, 1971, 16(6): 806-816.

[7] 史忠科. 固定区间平滑新算法及其在飞行试验中的应用[J]. 自动化学报，1991，17(3)：323-329.

SHI Zhong-ke. A new algorithm of fixed-interval smoother and its application to flight test[J]. ACTA Automatic Sinica, 1991, 17(3): 323-329.

[8] 宫晓琳，张蓉，房建成. 固定区间平滑算法及其在组合导航系统中的应用[J]. 中国惯性技术学报，2012，20(6)：687-693.

GONG Xiao-lin, ZHANG Rong, FANG Jian-cheng. Fixedinterval smoother and its applications in integrated navigation system[J]. Journal of Chinese Inertial Technology, 2012, 20(6): 687-693.

[9] Kalman R E. A new approach to linear filtering and prediction problems[J]. Transactions of the ASME--Journal of Basic Engineering, 1960, 82(1): 35-45.

[10] Gong X L, Qin T T. Airborne earth observation positioning and orientation by SINS/GPS integration using CD R-T-S smoothing[J]. Journal of Navigation, 2014, 67(2): 211-225.

[11] Ait-El-Fquih B, Desbouvries F. On Bayesian fixed interval smoothing algorithms[J]. IEEE Transactions on Automatic Control , 2008, 53(10): 2437-2442.

[12] Särkkä S. Bayesian filtering and smoothing[M]. Cambridge University Press, 2013: 139-142.

[13] Liu H, Nassar S, El-Sheimy N. Two-filter smoothing for accurate INS/GPS land-vehicle navigation in urban centers[J]. IEEE Transactions on Vehicular Technology, 2010, 59(9): 4256-4267.

[14] Shin E. Estimation Techniques for low-cost inertial navigation[D]. Calgary: The University of Calgary, 2005.

[15] Jouni H, Arno S, Särkkä S. Optimal filtering with Kalman filters and smoothers: a manual for the Matlab toolbox EKF/UKF[R]. Aalto University, 2011: 11-13.

[16] Shortelle K J, Graham W R, Rabour C. F-16 flight tests of a rapid transfer alignment procedure[C]//Position Location and Navigation Symposium. USA, 1998: 379-386.

[17] Yu J, Lee J G, Park C G, et al. An off-line navigation of a geometry PIG using a modified nonlinear fixed-interval smoothing filter[J]. Control Engineering Practice, 2005, 13(11): 1403-1411.

基于CWPA模型的最优平滑算法性能及其应用

程建华1,2，陈岱岱1，赵 琳1，王冰玉1，Rene Landry2

Performance and application of optimal smoothing algorithms based on CWPA model

CHENG Jian-hua1,2, CHEN Dai-dai1, ZHAO Lin1, WANG Bing-yu1, Rene Landry2
(1. College of Automation, Harbin Engineering University, Harbin 150001, China; 2. Ecole de Technologie Superieure, Université du Québec, Montreal H3C 1K3, Canada)

Aiming at the smoothing problem in linear Gaussian systems, the RTS smoother and two-filter smoother were analyzed. A novel RTS smoother was proposed which need less filtering data to be stored than that of traditional one. By taking into account the in-plane motion tracking problem, a continue Wiener process acceleration(CWPA) model was introduced. Based on the CWPA model, the estimation performances of Kalman filter, RTS smoother and two-filter smoother were studied by simulation. The results show that the estimation effects of the two smoothers are equivalent, and both are better than that of Kalman filter. Finally, according with the framework of two-filter smoother, a two-smoother-based transfer alignment accuracy evaluation approach for airborne slave inertial navigation system was presented. Compared with the conventional schemes in which only single smoother is adopted, this new approach can get better overall smooth performance. In particular, it improves the smoothing-based estimation performance of horizontal attitude misalignment.

optimal smoothing; Kalman filter; RTS smoother; two-filter smoother; continue Wiener process acceleration model; transfer alignment accuracy evaluation

1005-6734(2014)06-0748-07

10.13695/j.cnki.12-1222/o3.2014.06.009

U666.1

A

2014-07-19；

2014-11-13

国家自然科学基金（61374007, 61104036）；中央高校基本科研业务费专项资金（HEUCFX41309）

陈岱岱（1988—），男，博士研究生，从事组合导航技术研究。E-mail：ins_dai@163.com

联 系 人：程建华（1977—），男，副教授，硕士生导师。E-mail：ins_cheng@163.com