约束剖分的含断层地质体三维构模方法

王 威，徐亚杏，汪振东，张 炯，高一鸣

武汉工程大学资源与土木工程学院，湖北武汉 430074

0 引言

三维地质建模与可视化技术［1］是通过获取原始地质勘探数据如地质图、地形线、剖面、钻孔等，解译地质对象，利用各种信息形成一个复杂三维模型的过程，从而实现可视化.我国对于研究简单地质体的建模技术还是比较成熟的，但对于复杂地质现象(如断层、透镜体、岩石破碎带、地层倒转等)研究得还不特别深入［2］.

目前，国内使用的断层建模方式主要有基于地层恢复的建模技术(整体法)、基于分区插值的建模技术(局部法)、断层与地层的统一建模技术三类.本文基于统一建模技术方法，分析城市地质断层数据的特点，将断层线等各种边界线作为约束边插入，重新进行三角剖分，生成Tin(Triangulated Irregular Network)模型.当勘察数据更新或地质认识改变时，只需重新调整断层特征线，便可在调整部分生成新的断层模型来进行实时更新.通过实际应用，相较于其它方法，此法更尊重原始地质勘察数据，特别是在建造大型三维地质体模型时，大大节省了时间，同时保证了模型的准确性，使模型更加符合真实地质情况.本文最后以武汉市汉阳区为研究对象建立了三维地质模型，分析其中某一小块断层模型的生成过程，验证了此构模方法的有效性.

1 含断层地质体的生成原理

含断层地质体的生成主要采用多源数据耦合的建模方法(如图1)，通过勘探数据，如收集的钻孔资料、地表地质图、基岩地质图、地质剖面(利用钻孔人工生成剖面并通过实地考察检验和地质专家的分析来确定是否合理，如合理，即采用)等信息作为参考，利用带约束Delaunay三角网建立断层面、第四系地层面和基岩面等的 TIN模型，再通过手动拼接轮廓线对某一地层的顶面与底面缝合，形成一个完整的地质体模型.

2 带约束边的Delaunay三角剖分法

约束三角剖分就是利用约束条件，影响三角剖分的过程，或者在三角剖分之后根据这些约束条件去调整三角网.在地质曲面重构的过程中地表模型的断裂线、地质剖面的断层线和地层边界、地质图上的地形线等都可作为重要的约束条件.此方法的基本思路是:首先，利用无约束的点集生成初始Delaunay三角网，再将较复杂的地质中的特征线作为约束线依次插入到初始三角网中来重新调整初始三角网，使之符合Delaunay三角网的基本特性，最后就形成了带约束的Delaunay三角网.

图1 城市三维建模流程图Fig.1 City 3d modeling flowchart

2.1 无约束点集生成Delaunay三角网过程

设点集S里有n个离散点.

①寻找点集周围离质心最近的点作为起始点，假设为点O;②计算出中心点和点集内其余n-1个点的方向角、距离，升序排列其他所有点的倾斜度、方向角和距离的大小;③将O点和其他n-1个点连接成扇形依次进行径向扫描;再连接扇形的两个角点，形成初始三角网(图2-A);④从扇形边的任一点开始，按顺时针或逆时针方向凹侧连接，如图2-B所示.假如以a为起点，规定按沿逆时针方向逐一查找，a和b的下一个点分别是b和c，如果c点出现在线段ab方向的左侧，则b点选为当前点，从b点继续向前查找;如果c点出现在线段ab的右侧，就连接 ac，形成新三角形△abc(如图2-B)，继续向下搜索.同理，d点在ac的右侧，连接ad，又生成新的三角形△acd，继续查找d的下一个点e，发现点e在ad的左侧，则d仍为当前点，继续以d点向前查找，直到将凹多边形全变成凸多边形为止(如图2-C).当径向三角形极点被连接并第一次扫描径向三角形外边时，需要用一个数组记录外包边上的相邻边，则下一次扫描时就可以直接定位到下条边［3］.⑤以边界内某一三角形为起始三角形，开始对凸四边形的对角线依次检查，这些对角线是由两个相邻三角构成的，最终成功的最优三角剖分(如图2-D).

图2 径向扫描算法图解Fig.2 Diagram of the radial scan algorithm

以上过程表明:径向扫描算法的基本思想是先径向扫描离散点，构建初始扇形三角网，然后从扇形的任一点开始按一定方向进行凹侧连接，直到把外边界变成凸多边形为止.用局部优化算法调整到最优.

2.2 在Delaunay三角网中嵌入约束边

本文的初始三角网是通过Delaunay三角剖分算法中的径向扫描算法获得的，与带约束关系的离散点相关，下面介绍将带约束关系的约束边嵌入到初始三角网的具体方法.

建立一个存在的三角形集合T(V;L)，MT⊆T(V;L)，由MT中三角形的外边构成的多边形称为影响多边形 Q={pi，V1，V2，…，VK，pj，…，pi};设要插入的约束边为 l，l=pipj，pipj∈V，与约束边 l相交的三角形所组成的区域即为约束边l的影响域;

对于影响多边形Q，Floria［4］给出了如下的性质:

①简单多边形Q被对角线pipj分成Qu和Qd两部分，且Qu和Qd也为简单多边形，如图3所示.

根据“配第—克拉克”定律，在一个国家或地区的经济发展过程中，符合产业结构演变的基本规律是第一产业在国民经济中的比重会越来越少，而第二、第三产业所占比重将不断加大。农业在国民经济中的地位将会随着工业化和现代化进程被工业和服务业所逐步取代，这也是一个国家和地区的产业结构从低级向高级优化的必然过程。国内学者杨琳、李建伟（2002）采用第二、第三产业增加值之和与当年国民生产总值的比值（ISR）来衡量一个国家或者地区产业结构的变化。用公式表示则如下所示：

②Qu和Qd能被三角剖分.

③VK∈Q，若 VK为到 pipj的最近点，且(VK≠pi，VK≠pj)，则一定有

piVK∈Q，VKpj∈Q

图3 pipj作为约束边的影响域Fig.3 The influence domain of pipj as constraint boundary

在Delaunay三角网内插入约束边pipj的算法如下［5］:

①从三角网中找到以pi为顶点的三角形t1，且t1与pipj相交.如图4所示.

图4 首三角形的确定Fig.4 The determination of the first triangle

②从t1开始通过三角形的拓扑信息的搜索，发现影响域内三角形t1、t2、…，tk，将这些三角形保存在影响域三角形阵列中，同时生成Qu和Qd影响域的边界阵列，见图5.

图5 pipj边的影响域的确定Fig.5 The determination of the influence domain of pipj boundary

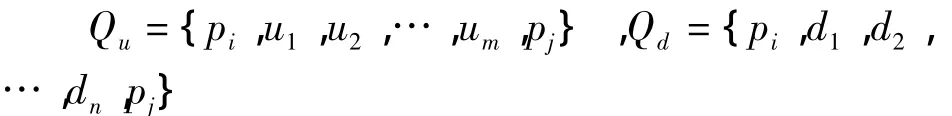
③为了在影响域内生成一个新的三角形，从一开始就pipj使用递归算法，同时将三角形的新一代信息保存在影响域三角形阵列的三角形空间中.

3 汉阳区含断层地质体模型的建立

3.1 工程背景

武汉市汉阳图幅位于经度114°～114°15'，纬度30°30'～30°40'.区内(如图6)第四系分布十分广泛(图中地表区域即为第四系地质)，占图幅总面积的90%以上，发育齐全，成因类型多样，通常按照时代四分法进行划分，即早更新世、中更新世、晚更新世和全新世.

3.2 汉阳区建模过程及成果展示

汉阳区含断层地质体三维模型(图6)主要是由带约束的Delaunay三角剖分得到的三角面构建的.此次模型的构建数据(如图1)主要来自于:①地表地质图;②基岩地质图;③钻孔;④含断层线的剖面;⑤地表等高线和地表以下各地层等深线等.

根据汉阳城市地质的数据特点，此次建模分3个步骤:a.首先对建模区数据进行预处理(包括钻孔数据的整理、确定钻孔标准分层、进行剖面交叉处一致性检查、建模区域单元格的划分等)，生成初始数据点(如图7);b.对数据点进行Delaunay三角剖分，形成DT剖分三角形(如图8);c.将地表等高线、地形线、剖面线(含断层线)等线形数据插入到第2步生成的三角网中，通过这些步骤完成对汉阳区数据的约束三角剖分(如图9)，最终生成汉阳区含断层地质体的三维地质模型(如图6).

图6 汉阳区三维地质体Fig.6 3D geological body in Hanyang District

图7 地表离散点Fig.7 The surface of the discrete points

图8 地表无约束的三角网Fig.8 Unconstrained surface triangulation

图9 地表嵌入约束边的三角网Fig.9 Constraint edge embedded in the surface triangulation

图7～图9都是以地表嵌入约束边三角剖分为例，下面以剖面上的约束线为例，详细阐述汉阳区地质体三维建模过程:

a.观察剖面上有各种约束线，通过剖面可推断此处有一个正断层，如图10加粗线即为断层线.

b.观察基岩地质图和剖面图相交部分(如图11)，发现此处单元格①中断层位于基岩面以下.

图10 汉阳区部分剖面形成的单元格①Fig.10 Part profile forming cell① in Hanyang

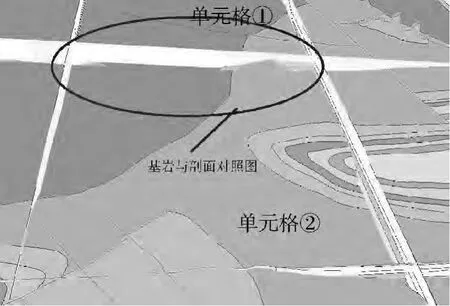
图11 基岩面与剖面对照图Fig.11 The comparison chart of bedrock surface and profile

将剖面上的约束线插入到初始三角网中，在剖面上人工交互建模，可先构造断层的下盘(如图12)，构建下盘时通过由外向内或由内向外层层构建，最终整个断层体构建完毕，(如图13).通过以上方法，可以对每个地层面逐一构建，再通过手动拼接轮廓线对每一地层的顶面与底面缝合，形成一个完整的地质体模型(如图14).如果想添加剖面分层数据或是更改对地层的认识，即可将新的特征约束线插入新的初始三角网，重新构建此单元格地质体.

图12 断层下盘最外圈地质体Fig.12 The outer ring geological body in the footwall

图13 断层地质体三维图Fig.13 3d geological fault

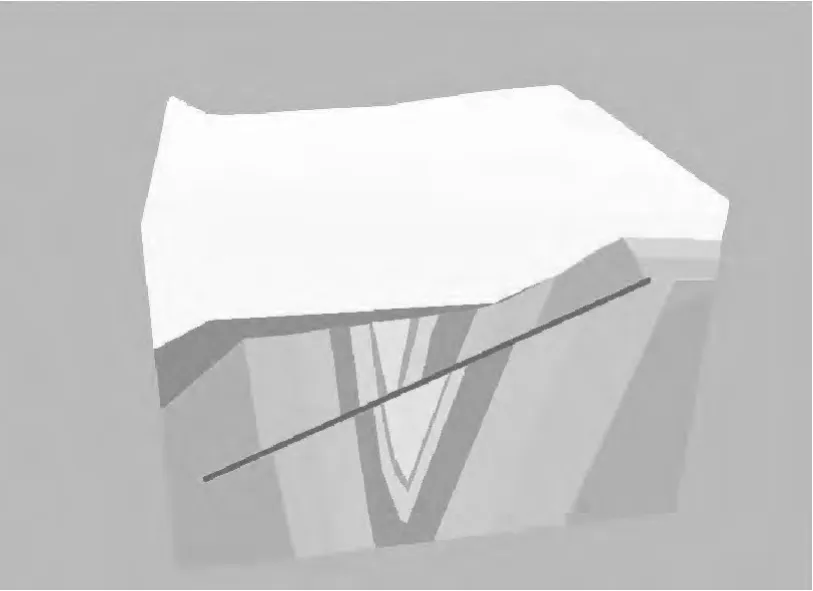
图14 单元格①中完整地质体Fig.14 Complete geological body in cell①

4 结语

通过对汉阳区城市地质数据信息的分析，建议选用带约束的三角剖分先生成TIN(不规则三角网)面，最终生成复杂三维城市地质体的方法.采用这种方法，集合了各种点集和特征线(地表等高线、地表地质图上的地形线、剖面上的地层线和断层线、基岩地质图上的基岩分界线和断层线、各地层的等深线等)，并将这些数据作为约束点和约束线插入进行带约束的三角剖分.因为耦合了多源数据，所以模型的精度更高.本文算法已在Visual C++6.0中得以编程实现，并在武汉市汉阳区城市地质三维模型建立中得以应用.为城市三维地质的发展奠定了基础.

［1］ZHONG D H，LI M C，SONG L G，et al.Enhanced NURBS modeling and visualization for large 3D geoengineering applications:an example from the Jinping first level hydropower engineering project，China ［J］.Computer and Geosciences，2006，32(9):1270-1282.

［2］何赵云，李章林，张夏林.含断层地质体三维建模技术［J］.软件导刊，2010，9(8):175-177.HE Zhao-yun，LI Zhang-lin，ZHANG Xia-lin.3d geological faults modeling technology ［J］.Software Guide，2010，9(8):175-177.(in Chinese)

［3］林报嘉，叶燕林，赵建伟.三角网的生成与简化算法［J］.地理学与国土研究，2001，17(1):69-72.LIN Bao-jia，YE Yan-lin，ZHAO Jian-wei.The estab-lishment ands simplification algorithm of TIN［J］.Geography and Territorial Research.2001，17(1):69-72.(in Chinese)

［4］Floriai LD.An on-line algorithm for constrained delaunay triangulation［J］.CAGIP:Graphical Models and Image Processing，1992，54(3):290-300.

［5］宋占峰，詹振炎，蒲浩.Delaunay三角网剖分中嵌入约束边的局部调整算法［J］.西南交通大学学报，2002，37(4):399-403.SONG Zhan-feng，ZHAN Zhen-yan，PU Hao.A local adjustment algorithm for inserting constrained segments in delaunay triangulation［J］.Journal of Southwest Jiaotong University，2002，37(4):399-403.(in Chinese)