几种不同信道下Turbo码的误码率性能分析

张 磊，王 锦

（天津职业技术师范大学电子工程学院，天津 300222）

半个多世纪以来，伴随着通信技术的飞速发展以及各种传输方式对可靠性要求的不断提高，信道编码技术占据越来越重要的地位。香农的信道编码定理提出，在有噪声信道中，当信息传输速率小于信道容量时，总可以找到一种编、译码方法，使误码率任意小。Turbo码作为一种新的编码结构，在信噪比为0.7dB时，误比特率（BER）可达10-5。本文根据Turbo码的编、译码原理，分析Turbo码的误码率影响因素，并对比其在几种典型信道下的误码率。

1 Turbo码的编码原理

Turbo码是Berrou提出的一种并行级联循环系统卷积码，它由2个循环系统卷积码编码器通过随机交织器并行级联而成，编码后的校验位经过适当的删余，最后产生满足一定码率要求的码字，其结构如图1所示[1]。

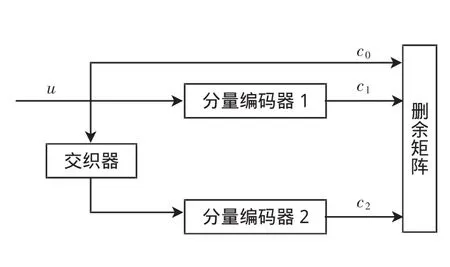
图1 Turbo码编码器

从图1中可以看出，信息序列u直接进入分量编码器1产生校验位c1，相同的信息序列经过交织器后再进入分量编码器2产生检验位c2。通常情况下，图1中的2个编码器是相同的。交织器的目的是为了实现随机性编码，采用循环系统卷积码（RSC），将普通卷积码中的输出作为反馈迭加到输入端。由于Turbo码是系统码，因此信息序列直接输出产生c0，即c0等于u。由图1可得，输入一个信息位可产生三位输出，若没有删余矩阵，Turbo码的码率为1/3，否则码率为1/2，这样可提高传输速率。

2 Turbo码的译码原理

Turbo译码的最大特点是引入迭代译码思想。Turbo码译码器如图2所示，由2个分量译码器并行级联构成。它们对应于编码器中的2个分量编码器1和2，译码器和编码器中所使用的交织器相同，解交织器和交织器需要配套使用。每一个分量译码器对分量码进行最佳译码，都可以产生一个外部信息的变量L1e（xk）或L2e（xk），此变量在迭代过程中被传递。在第一次译码时，译码器1的输入只有接收到的信息序列和对应于第一个编码器产生的校验位的接收比特，它们经过译码器后计算出外部信息的变量L1e（xk）。在Turbo码的编码器端，由分量编码器2产生的校验位是经过交织后的信息序列产生的，因此在译码时，译码器2的输入是、经过交织后的系统位及L1e（x′k）。译码器2的输出经过解交织后作为下一次的输入再传输给译码器1，这样就形成了迭代过程。经过多次迭代后，译码器1和2的外信息逐渐稳定。通常仿真时都把迭代次数以经验值固定，到达预定的迭代次数后，译码器2的输出经过解交织后就可以得到信息比特的对数似然比。

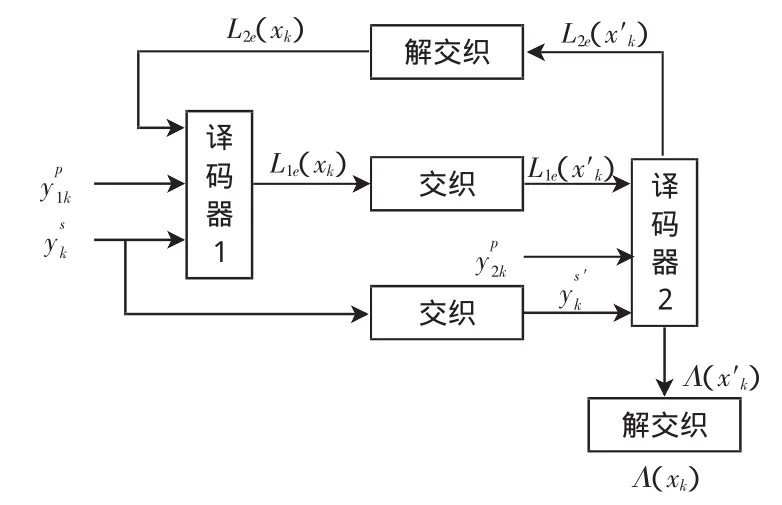
图2 Turbo码译码器

3 Turbo码的译码算法及主要物理信道

Turbo码要求有一种软输入软输出（SISO）的译码算法。软输出译码器的输出包含硬判决值和做出这种判决的可信程度，常用对数表示法，若接收码字为r，则对数似然比为：

式中：P{dk=1/r}和P{dk=0/r}分别代表接收码r时发送码dk=1和dk=0时的条件概率，按照下列判决规则进行判决：

可见，L（dk/r）的符号代表硬判决值，L（dk/r）的绝对值代表硬判决的可信度。绝对值越大其可信度也越大。

常见的Turbo码译码算法有两类：一类是最大后验概率（MAP）算法及其简化算法，如对数MAP（Log-MAP）算法和最大值（Max-Log-MAP）算法；另一类是软输出维特比（SOVA）算法。从算法复杂度而言，MAP算法最为复杂，Log-MAP其次，之后是Max-Log-MAP算法，SOVA算法最简单。从算法的性能来说，MAP算法最优，Log-MAP算法次优，其次是Max-Log-MAP，SOVA算法的性能是最差的。直接执行的MAP是计算密集型的，不可用于实时应用系统中。Log-MAP算法就是对标准MAP算法中的似然用对数来表示，乘法运算则变成加法运算。参考文献[2]和[3]对Turbo码的译码算法进行了较详细的介绍。为了减少译码的复杂度，Turbo码译码算法可采用Log-MAP算法。

研究表明，Turbo码在AWGN信道条件下具有优异的译码性能。但是在实际的移动通信系统中，衰落信道模型更能体现信道的特性[4]。因此，衰落信道上Turbo码的性能研究和分析也很重要。

AWGN信道是一种加性噪声信道。这种噪声是假定在整个信道宽带下功率谱密度为常数，并且振幅符合高斯概率分布。

在无线信道环境中，电磁波经过反射、折射、散射等多条路径传播到达接收机后，总信号强度服从瑞利分布。同时由于接收机的移动及其他原因，信号强度和相位等特性又发生起伏变化，故称为瑞利衰落。瑞利分布是一个均值为0、方差为σ2的平稳窄带高斯过程。其数学表达式为：

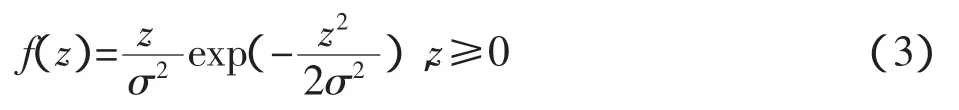
如果收到的信号中除了经反射、折射、散射等来的信号外，还有从发射机直接到达接收机信号，那么总信号的强度服从莱斯分布，故称为莱斯衰落。正弦波加窄带高斯过程的包络概率密度函数分布称为莱斯分布，也称广义瑞利分布。其数学表达式为：

式中：参数A指主信号幅度的峰值；I（0）为修正的0阶第一类贝塞尔函数。莱斯因子为K=A2/（2σ2），其定义为确定信号的功率与多径分量方差之比。当K=0时，莱斯分布转变为瑞利分布；反之，趋于∞时则转变为高斯分布。

4 不同信道模型下的误码率性能分析

这里主要分析Turbo码在不同信道模型下的误码率性能，选取的信道有以加性噪声为主的AWGN信道、Rayleigh衰落信道以及Rician衰落信道。

为了节省Turbo码的译码时间，这里选取码率为1/2。图3给出了交织长度为400时Turbo码在不同信道下的误码率曲线。其生成矩阵为（7，5），采用BPSK调制方式，循环迭代5次，译码算法采用Log-MAP算法。

图3 交织长度为400时迭代5次Turbo码在不同信道下的误码率

图4给出了交织长度为800时Turbo码在不同信道下的误码率曲线。其生成矩阵为（7，5），采用BPSK调制方式，循环迭代5次，译码算法采用Log-MAP算法。

图4 交织长度为800时迭代5次Turbo码在不同信道下的误码率

图5给出了交织长度为800时Turbo码在不同信道下的误码率曲线。其生成矩阵为（7，5），采用BPSK调制方式，循环迭代10次，译码算法采用Log-MAP算法。

图5 交织长度为800时迭代10次Turbo码在不同信道下的误码率

从仿真结果可以看出，如果采用衰落信道，则会降低Turbo码的译码性能。整体来看，Turbo码在AWGN信道下的译码性能最好，误码率最低；在Rayleigh衰落信道下的误码率性能最差；在Rician衰落信道下的误码率性能介于AWGN信道和Rayleigh衰落信道之间，并且随着莱斯因子的增大而提高[5-7]。还可以看出，当信道噪声比较大时，Turbo码在几种信道中的误码率差异比较大，但是随着信噪比的增加，即信道噪声越来越小时，信道对Turbo码误码率的影响差异逐渐减小，而且Turbo码在几种信道中的误码率性能曲线明显弯曲，意味着其误码率性能几乎呈线性改善。

对比图3和图4可以看出，随着交织长度的增加，Turbo码在几种信道下的纠错能力都随之提高。但随着序列的增长，性能改善速度越来越慢。而且随着信噪比的增大，Turbo码在几种信道中的误码率性能接近。交织长度的增加不会加大译码复杂度，但是会延长译码时间[8]。在仿真过程中也发现，随着交织长度的增加，译码所需时间也越来越长。

从图4和图5可以看出，随着迭代次数的增加，Turbo码的误码率性能不断改善，但是Turbo码在Rician衰落信道中的误码率性能改善程度要比在Rayleigh衰落信道好，而在AWGN信道中的改善最明显。但是，在迭代到一定次数后性能将趋于饱和。这是因为多次迭代后，译码器已经对输入码字有了一个轮廓，进一步的信息交换不能再提供更多的新信息。一般Turbo码在迭代5～10次之间达到饱和，即可进行判决。随着迭代次数的增加，编码增益逐渐减小，但计算量持续增加。Turbo码在不同信道下的优缺点及其适合的环境归纳如下：

（1）Turbo码在AWGN信道中的误码率最低，但AWGN信道主要是加性高斯白噪声，其应用范围比较窄，只适用于恒参信道，如卫星通信[9]。

（2）从Turbo码在Rayleigh衰落信道中的误码率曲线改善可以看出，Turbo码具有良好的抗多径衰落和抗多径效应性能，适合用于密集的建筑和其他物体使得无线设备的发射机和接收机之间没有直射路径且信号被衰减的信道，如筑物密集的城镇中心地带[10]。

（3）Turbo码在Rician衰落信道下的误码率性能要优于Rayleigh衰落信道。但是只能当移动台与基站之间存在直射波信号，即存在一条主路径传输幅度和相位都稳定的信号时，Turbo码在Rician衰落信道中的优势才明显，其更适合无障碍长距离无线移动通信。

5 结束语

信道编码是提高信号在无线衰落信道中可靠传输的重要工具。本文对Turbo码在不同衰落信道中的误码率性能进行了比较分析，从以上Turbo码在不同衰落信道中的优缺点和其适用的无线通信环境可以说明Turbo码是一种非常有应用前景的高效纠错码型。

[1]王琳，徐位凯.高效信道编译码技术及其应用[M].北京：人民邮电出版社，2007：63-64.

[2]刘东华，梁光明.Turbo码设计与应用[M].北京：电子工业出版社，2011：51-64.

[3]刘东华，唐朝京.用于Turbo迭代译码的Log-MAP算法的简化[J].电子与信息学报，2001，23（12）：1340-1347.

[4]李俊.无线衰落信道的建模与仿真研究[D].西安：西安电子科技大学，2008.

[5]朱立君，杜栓义，邱长兴.基于AWGN信道的Turbo码性能分析[J].西安电子科技大学学报，2007（7）：20-23.

[6]MARSLAND IanD，MATHIOPOULOSP Takis.Multipledifferential detection of parallel concatenate convolutional（Turbo）codes in correlated fast rayleigh fading[J].IEEE J Selected Areas in Commun，2001，19（2）：265-275.

[7]俞济洋.Turbo码在Ricain衰落信道上的性能分析[J].哈尔滨师范大学自然科学学报，2013，29（3）：52-54.

[8]王莹.Turbo码中几个关键技术研究[D].西安：西安电子科技大学，2006.

[9]姚行俊，薛质，徐友云.Turbo乘积码在卫星通信中的应用[J].无线电通信技术，2004，30（2）：11-12.

[10]孙宁宁，达新宇，闫大勇.Turbo码在慢衰落信道中的性能分析及应用[J].空间电子技术，2004（3）：41-45.