2K-V型减速机的动力学建模与实验研究

刘长坤，李充宁，杨保占，高 岭

（1.天津职业技术师范大学机械工程学院，天津 300222；2.国网安徽省电力公司，合肥 230061）

2K-V型减速机是在摆线针轮传动的基础上发展起来的一种新型减速机。与传统的行星减速机相比，其具有速比范围大、精度高、刚度高、效率高、承载能力强以及体积小等优点。国内对2K-V型减速机已经有不少研究。在对其动力学建模分析方面，已经有人建立了13个自由度的弯扭分析模型[1-2]，但在分析影响系统一阶固有频率的主要因素方面不够明确；有人用传递矩阵的方法建立了动力学分析模型[3]，但其只考虑曲柄轴的扭转刚度、弯曲刚度和输入轴的扭转刚度对整机系统动力学特性的影响；有人结合渐开线齿轮传动副与摆线针轮传动副的啮合刚度的作用关系，并用惯性盘模拟工作负载，对系统简化形成了5个自由度的扭转动力学模型[4]。该模型主要涉及扭转运动，没有考虑各个构件的径向振动，不能有效地进行振动响应的计算和分析。由于轴承刚度对系统动态性能的影响比较大，上述分析模型中没有考虑轴承刚度的影响。

本文采用集中质量法，建立包含轴承刚度及构件径向振动影响的动力学模型，并试图利用所建的模型求解对该类减速机影响较大的前两阶固有频率理论值，再进行相关试验验证。

1 2K-V型摆线针轮传动受力分析

2K-V型减速机中摆线轮的受力分析如图1所示。图1中，摆线轮与针齿为多齿啮合，每一个针齿与摆线轮的啮合力的作用线相交于节点P，并且在P点处合成总的啮合力F，F沿节圆分解为切向力Fpt和径向力Fpr。由受力图可知，摆线轮的节点位于齿根圆以内，总啮合力F的径向分力Fpr沿着偏心方向向外，与x轴的夹角为φ；切向力Fpt的方向与x轴的夹角为φ-90°。这2个力的大小分别为[5]：

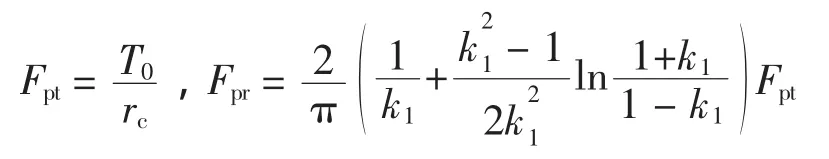
式中：rc为摆线轮节圆半径；k1为短幅系数，通常k1=0.55～0.8。

图1 摆线轮受力分析

曲柄轴承对摆线轮的作用力Ri可以分解为Rif和Rit两部分：Rif为与轮齿啮合作用力和曲柄轴承的离心力的合力相平衡的分力；Rit为与Fpt产生的力矩平衡的的分力，大小分别为：

式中：ωH、ωc分别为曲柄轴的公转和自转角速度；a为偏心距；r0为曲柄轴的分布圆半径；N为曲柄轴的个数；T0为输出转矩。

Rit的方向沿ωH的转向切于半径为r0的圆，各个Rit之间的夹角为360°/N，Rif的方向与x轴正向的夹角为90°+φ+β，其中：

由式（2）至式（4）可以看出，在外载荷和输出转矩不变的情况下，Rit的大小恒定，方向不变；Rif的大小恒定，方向随曲柄轴转角变化，但是与曲柄轴的相位差恒为90°+β。

2 2K-V型减速机动力学建模

2.1 模型分析

2K-V型减速机因型号不同，曲柄轴的数目不同，建立的动力学模型也不尽相同，但是曲柄轴为对称分布时，建立动力学模型有一定的规律性。本文以3个曲柄轴的2K-V320S型减速机为例，采用集中参数法建立整机系统动力学模型。根据减速机的结构特征，整机的系统动力学模型建立在以下假设上：①曲柄轴曲柄段的滚针轴承和两端的支撑轴承在模型中都用拉压弹簧表示，其刚度为定值。②忽略齿轮啮合中综合刚度的变化，设齿轮啮合刚度为常数。③计算摆线针轮的啮合刚度时，啮合力按集中力处理，大小方向与β相同。其动力学模型如图2所示。

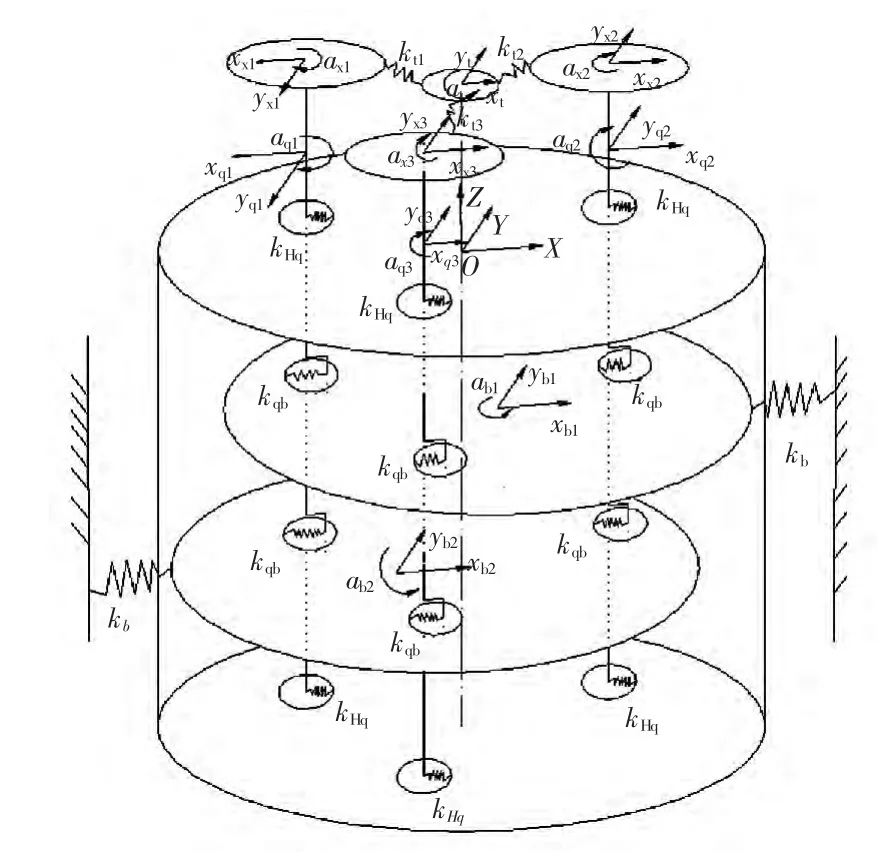
图2 系统动力学模型

参考坐标系O-xyz建立在行星架上，以行星架轴线的中点为坐标原点，z为轴向，x的方向由原点指向第一个曲柄轴轴孔的几何中心，该坐标系绕其轴线以角速度ωv转动。在O-xyz坐标系中其他构件的坐标系为：

（1）输入齿轮轴（太阳轮）坐标系（xt，yt，αt），xt、yt为径向坐标，方向与x、y相同，αt表示输出齿轮轴绕其轴线的回转角。

猪瘟俗称“烂肠瘟”，它是由猪瘟病毒引起的一种高度接触性传染病。猪瘟病毒（CSFV）属于黄病毒科猪瘟病毒属，CSFV为单股正链RNA有囊膜病毒。自1833年首次在美国俄亥俄州发现CSF。近百年以来，一直在全世界范围内流行，也是目前危害我国养猪业发展的主要疫病之一。中国自主研制的猪瘟兔化弱毒疫苗在防治CSF过程中具有很重要的作用，但近年来各地生猪养殖场仍有CSF免疫效果不理想的情况出现。

（2）行星轮坐标系（xxi，yxi，αxi），i=1，2，3表示行星轮号。xxi、yxi为径向坐标，xxi的方向出太阳轮几何中心指向行星轮i的几何中心，αxi表示行星轮i绕其轴线回转角。

（3）曲柄轴坐标系（xqi，yqi，αqi），i=1，2，3表示曲柄轴号。xqi、yqi为径向坐标，坐标方向与配合的行星轮坐标方向相同，αqi表示曲柄轴i绕其轴线回转角。

（4）摆线轮坐标系（xbi，ybi，αbi），i=1，2，3表示摆线轮号。xbi、ybi为径向坐标，方向与x、y一致，αbi表示摆线轮i绕其轴线的回转角。

（5）行星架坐标系（xH，yH，αH），xH、yH分别与x、y的方向相同，αH表示行星架绕其轴线的回转角。

这样，系统共有10个运动构件，共30个自由度。

2.2 各运动构件的动力学方程

相接触的各构件之间因弹性变形产生反力，该力的大小与相对位移成正比。因此需要确定相互作用运动构件之间的相对位移。由图3以及各个构件的运动关系，可以确定相互作用构件之间的相对位移。

太阳轮（输入齿轮轴）受到行星轮的作用力、输入转矩的作用及轴承的支撑力。则由牛顿第二定律可列出太阳轮的动力学方程：

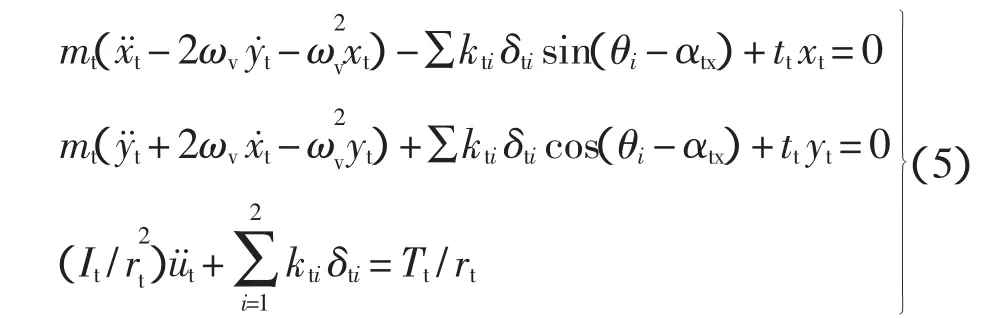
式中：ωv为行星架的理论转速；kti为太阳轮和行星轮i的啮合刚度；kt为太阳轮的支撑轴承刚度；mt为太阳轮质量；It为太阳轮转动惯量；Tt为输入转矩；δti为太阳轮和行星轮i在啮合方向上的相对位移为；θi=（i-1）2π/3；αtx为太阳轮和行星轮的啮合角；ut为太阳轮啮合线上的相对位移；rt为太阳轮的节圆半径。

同理，可推倒出行星轮i的动力学方程：

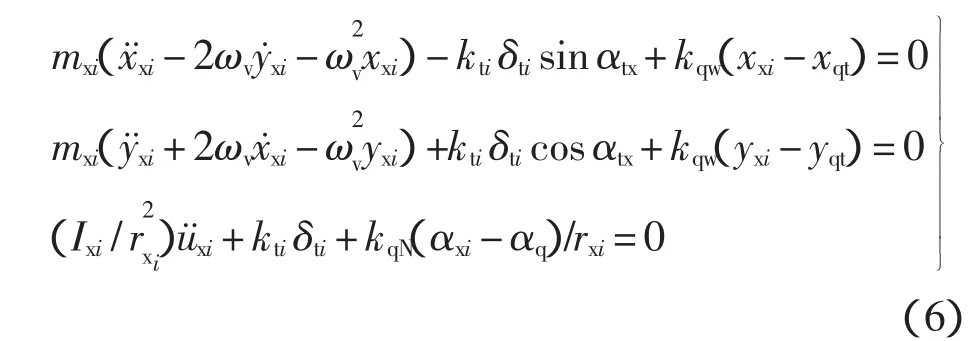
式中：mxi为行星轮i的质量；Ixi为行星轮i的转动惯量；kqw为曲柄轴的弯曲刚度；kqN为曲柄轴的扭转刚度；uxi为行星轮i啮合线上的相对位移。

2.2.2 曲柄轴动力学方程

曲柄轴受到摆线轮，行星轮和行星架3个构件的作用力，由牛顿第二定律得曲柄n（n=1，2，3）的动力学方程为：

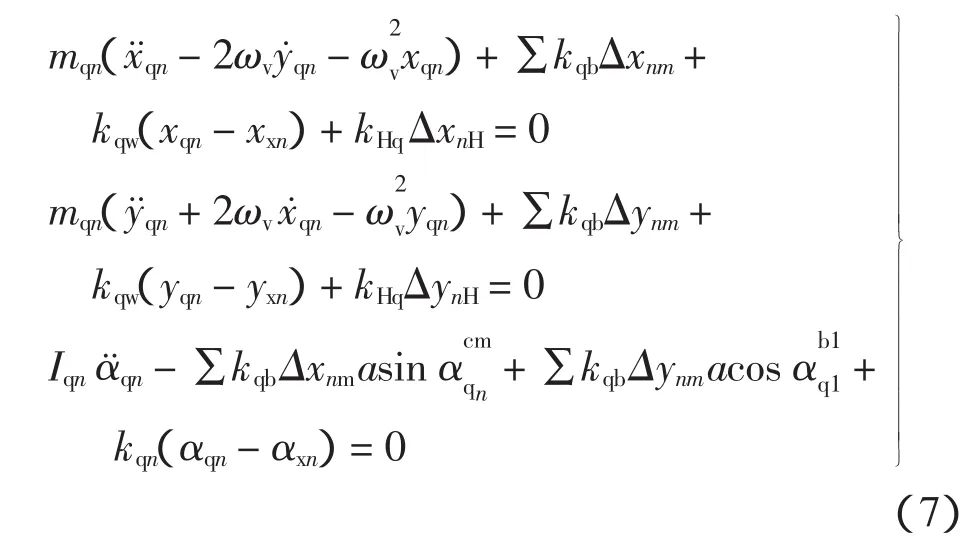
式中：mqn为曲柄轴n的质量；Iqn为曲柄轴n的转动惯量；kqb为摆线轮与曲柄轴之间的轴承刚度；kHq为行星架与曲柄轴之间的轴承刚度；a为偏心距π（m-1）为曲拐与曲柄轴坐标系xqn轴方向的夹角；Ψqn为曲柄轴n的坐标系和摆线轮坐标系的夹角为曲柄轴1的曲拐与曲柄轴1坐标系的xq1轴的夹角；为曲柄轴的初始相位角；Δxnm和Δynm分别为曲柄轴n和摆线轮m（m=1，2，3）的弹性相对位移；ΔxnH和ΔynH分别为曲柄轴n与行星架的弹性相对位移。

2.2.3 行星架的动力学方程

行星架只受到曲柄轴的作用力，由牛顿第二定律得其动力学方程为：

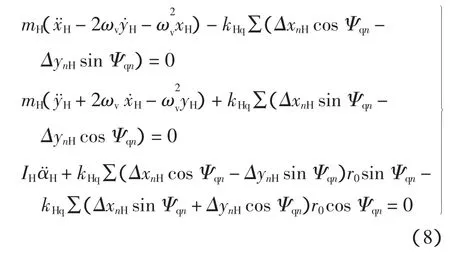
式中：r0为曲柄轴分布圆半径；mH为行星架的质量；IH为行星架的转动惯量。

2.2.4 摆线轮的动力学方程

摆线轮受到曲柄轴和针齿的作用力，则由牛顿第二定律可得摆线轮j的动力学方程：

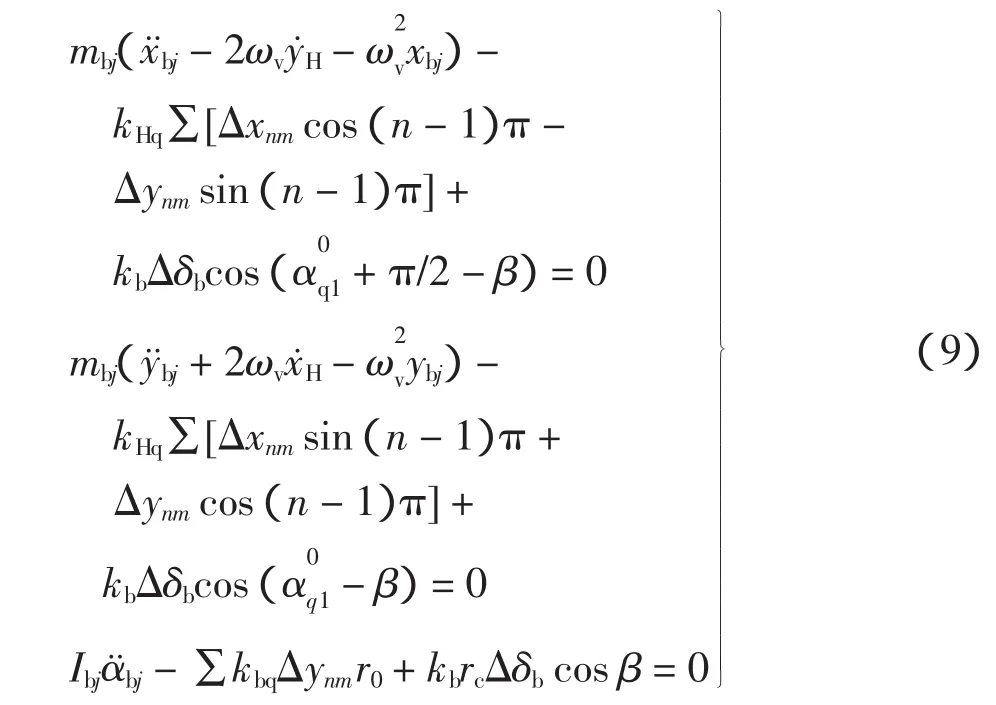
式中：mbj为摆线轮j的质量；Ibj为摆线轮j的转动惯量；kb为摆线轮针齿的啮合刚度；Δδb为摆线轮j与针齿啮合的啮合位移。

联立方程（1）至方程（5）并整理可得到系统的自由振动动力学方程：

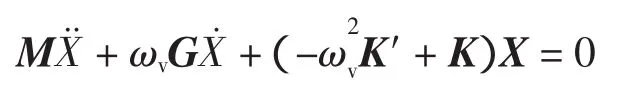
式中：M为质量矩阵；K为刚度矩阵；G为陀螺矩阵；K′为向心动刚度矩阵；X为广义坐标向量。

3 计算结果

本文所研究的2K-V320S型减速机的参数为：太阳轮齿数Z1=13，行星轮齿数Z2=71，模数m=1.5，压力角α =20°；摆线轮齿数Z3=39，针齿齿数Z4=40，偏心距a=2.2 mm，针齿销半径r=10 mm，针齿中心圆半径Rz=229mm；传动比[5]i=219.46；输出转矩T0=3136N·m；输出转速为15 r/min。

利用pro/e建立上述减速机的三维模型，在pro/e中可以直接测得各个构件的转动惯量；根据材料力学相关知识，可以计算曲柄轴的扭转刚度kqN；根据文献[4]可以计算渐开线齿轮的平均啮合刚度和摆线针轮的平均啮合刚度；根据文献[6]可以计算滚针轴承的径向支撑刚度kHq和kqb。经计算，系统自由振动的一阶固有频率为266 Hz左右，二阶固有频率为310 Hz左右。

通过锤击法实验，测得样机的前二阶固有频率分别为287 Hz和361 Hz，与理论计算得出的结果基本一致。

4 结束语

本文建立了包含轴承刚度和构件径向振动影响因素的2K-V型动力学分析模型。通过实例求解方程，得出了样机的前二阶固有频率理论值。同时，修改各个齿轮副相对位移的计算公式中的参数，就可以研究制造误差对系统动力学特性的影响。针对自主研发的样机，利用LMS测试系统做了固有频率测试，得到了样机的动态响应曲线，曲线上各个波峰位置可显示出样机的各阶固有频率。通过对比实验结果和理论计算结果，验证了所建模型的有效性。所测样机的前二阶固有频率比较高，应用在机器人上可以避免共振现象的发生，从而为机器人的平稳工作提供保证。

[1]刘继岩，孙涛，戚厚军.RV减速器的动力学模型与固有频率研究[J].中国机械工程，1999（4）：381-386.

[2]戚厚军.RV减速机动态特性分析[D].天津：天津大学，2001.

[3]李瑰贤，吴俊飞.变厚齿轮RV减速器系统扭振动力学分析[J].机械传动，1999（4）：20-22.

[4]张大卫，王刚，黄田.RV减速机动力学建模与结构参数分析[J].机械工程学报，2001，37（1）：69-74.

[5]李充宁，孙涛，刘继言.2K-V型行星传动的结构和力的分析[J].机械传动，2000，24（2）：7-9.

[6]陈忠.滚动轴承及其支撑刚度的计算[J].煤矿机械，2006，27（3）：387-388.