大学生考试成绩“扎堆”现象的统计分析
2014-10-18熊瑞生
熊瑞生
(信阳师范学院 土木工程学院,河南 信阳 464000)
教育行业的一个永恒的主体,就是如何有效地提高教育教学质量。要想有效地提高教育教学质量,就必须分析影响教育教学质量的原因;基于此目的,笔者用数理统计的方法,以寝室为单位分析了两个班级学生的考试成绩分布情况,用统计学的观点,分析了影响学生学习成绩的原因。
一、大学生考试成绩的“扎堆”现象及其种类
在大众化教育背景下,许多中学生走进了大学校门,但他们中的一些人,对自己走进大学校门的目的并不十分清楚,对自己以后应该干什么也不十分明白。再加上在高中阶段一些教师为追求升学率而采用了不正确的教育理念,例如,一些高中教师经常对高三的学生说:“辛苦就辛苦这一年啦,到了大学就轻松啦!”因此,一些高中生就错误地认为大学校园就是休闲娱乐的场所,是谈情说爱的场所[1]。那么,当他们带着这样的想法进入大学校园后,他们不可能有正确的学习目的和学习态度,因此也不可能有好的成绩。相反,另一些学生有学习积极性与主动性,他们进入大学后,经过一年级的波动与选择后,有了明确的学习目的和奋斗方向,并为此而不懈地努力,因此他们多门课程都取得了良好的成绩。所以,现在大学生的学习出了两极分化的现象,这一现象在普通二本院校中十分突出。这一现象导致了学生考试成绩“扎堆”现象的出现;进一步分析发现,这种扎堆现象又可细分“散发式”和“组团式”两种情况。下面分别进行论述。
1.“散发式”的考试成绩扎堆现象。
所谓考试成绩“扎堆”,就是一些学生每年都有若干门课程的考试成绩不及格,而另外一些学生,则是多数课程的考试成绩都在良好(80分)以上,达到优良等次。这种扎堆现象出现在少数学生身上,他们分散在多个寝室。出现这种现象的原因是一些学生要么基础很差,要么学习方法有问题而不适应大学的学习,要么学习态度和目的有问题不愿意学习,而是沉迷于网络、游戏或者其他与学习无关的活动中,从而多门课程不及格。而另外一些学生却有明确的学习目的,基础也比较好,并且奋发努力,因而多门课程的成绩都在优良等次。这种考试成绩扎堆现象,是“散发式”的,只集中在某些少数学生身上,而不是集中在某几个寝室。
2.“组团式”的考试成绩扎堆现象。
现在在高校里不仅出现了“散发式”的考试成绩扎堆现象,还出现了另一种形式的、以寝室为单位的考试成绩扎堆现象,即某几个寝室内多数学生的多门课程不及格,而另外几个寝室内的多数学生的多门课程的成绩为良好或优秀。姑且把这种考试成绩扎堆现象称之为“组团式”的扎堆现象。当出现这种情况时,对不及格情况扎堆的寝室内的学生,显然不能解释为这些学生都基础差,或者学习方法都不正确;同样地,也不能对成绩优良情况扎堆寝室内的学生解释为基础都好,或者学习方法都正确。笔者认为,出现这种现象的原因主要是以寝室为单位的学风(简称为“室风”)问题。因为他们在同一个学校、同一个班级,用同样的教材,由同一个教师授课;也就是说他们受教育的环境,除了寝室内的成员不同外,其他条件都是相同的。因此,考试成绩“组团式”扎堆现象的出现,应该主要是由室风的影响造成的。
二、考试成绩“组团式”扎堆现象的统计分析
对于“散发式”的、以学生个体为单位的成绩扎堆现象,很容易通过对照多门课程的成绩册进行判断,并能方便地找出多门课程不及格和多门课程优良的学生。但对于以寝室为单位的、“组团式”的成绩扎堆现象,却不能从成绩册上直接看出。因为我校在编排大一新生的寝室时,未按录取分数的高低和学号顺序编排,而是采用随机的方式编排,将不同分数、不同地区的学生编排在一个寝室里,以便不同中学教育背景、不同基础水平的学生能够相互帮助。由于不同学生对不同课程的理解和掌握程度不同,对相关基础课的掌握程度也不一样,所以不同程度的学生分散于不同的寝室中。因此从成绩册上看不出“组团式”的成绩扎堆现象。要判断有无这种形式的成绩扎堆现象,就要用数理统计的原理进行统计分析,因此需要选择统计分析的样本——即进行统计分析的班级。
1.统计分析班级的选择。
大一的学生,由刚从天天有人管着的高中阶段进入相对宽松、相对自由的大学后,因新鲜、新奇和放松,成绩波动很大,因此不能作为统计样本。到了大二后,一些学生的情绪、心思逐渐稳定下来,学生的学习成绩逐渐出现分化,但也有一些学生在大二上学期与下学期的成绩仍有较大波动,因为有人选择了放弃,有人选择了弥补和奋斗。因此用二年级的学生成绩作为统计样本,其结果也不太稳定。到了大三,基本上所有学生的奋斗目标、学习态度和学习方法都稳定下来了,因此,学生在大三上、下两个学期的学习成绩具有统计学上的稳定性,适于用来进行统计分析。本次统计分析选用了我校2010级土木工程专业(1)班和(2)班的学生成绩作为样本,并且选择两门在土木工程专业课程设置中的地位和作用均相同的《混凝土结构设计原理》和《钢结构设计原理》两门课程的成绩作为统计分析的样本。这两门课程分别开设在大三上学期和下学期,每门课程、两个班级均由同一个教师讲授。两门课程均采用闭卷考试的方式考核,两个班级学生的这两门课的成绩都符合正态分布。

表1 不同寝室两门课程的成绩优良率的数据表
2.统计分析指标的选择及统计分析结果。
选定统计分析的样本之后,就要选择统计分析的指标。为考查成绩分布是否有“组团式”的扎堆现象,选择以寝室为单位的成绩优良率(即成绩≥80分的学生占寝室人数的比率)和不及格率(即成绩<60分的学生占寝室人数的比率)两个指标分别进行统计分析,以便考查是否存在成绩优良情况和不及格情况的“组团式”的扎堆现象。这是一个双因素的方差分析问题,一个因素为成绩优良率G(或不及格率E),另一个因素为寝室D。因素G(或E)取两个水平,分别对应于《钢结构设计原理》的成绩比率和《混凝土结构设计原理》的成绩比率,因素D取s个水平,对应于s个寝室。为节省篇幅,本文只显示两个班级中的一个——土木(2)班的成绩统计结果。该班共有85人,其中男生54人、女生31人;分住在18个寝室中,男生寝室11个、女生寝室7个。其中混合(与其他专业的学生合住的)寝室6个,这6个寝室中,只有1个寝室住有5个该班的学生,其余5个混合寝室中住有该班的学生为1人或2人;统计分析中不考虑这5个混合寝室里学生的成绩情况,因为他们不符合统计条件。进行统计分析的寝室共13个(即因素D取13个水平),其中,男生寝室8个、女生寝室5个。有一个寝室住5人,其余寝室均为6人。
(1)优良率的统计分析。
如前所述,这是一个双因素的方差分析问题。以寝室为单位分别算出两门课程的优良率,具体结果见表1。表1中的G1、G2分别为《钢结构设计原理》和《混凝土结构设计原理》课程的成绩优良率,D1~D13为寝室的序号,其中D1~D8为男生寝室、D9~D13为女生寝室。
每个寝室的成绩优良率Xij可以表达为

其中,μG为成绩优良率的总平均值;αi、βj分别表示水平 Gi和 Dj的效应;εij为随机误差, 服从 N(0,σ2)分布。此时,要检验的原假设和对立假设[2]分别为:
原假设:H01:α1=α2=0
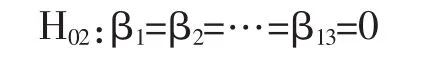
对立假设:H11:α1,α2不全为 0
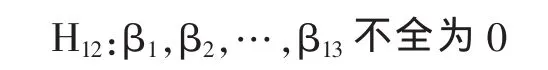
根据方差分析原理,对表1中的数据进行方差分析[3],分析结果见表2。在显著性水平a=0.05,即置信度1-a=95%时 F 的临界值为 F0.05(1,12)=4.75,F0.05(12,12)=2.69。 因为 FG(1,12)=1.51

表2 成绩优良率的方差分析表
(2)不及格率的统计分析。
以寝室为单位的两门课程的不及格率如表3所示。表3中的E1、E2分别为《钢结构设计原理》和《混凝土结构设计原理》课程的成绩不及格率。

表3 不同寝室两门课程的成绩不及格率的数据表
每个寝室的成绩不及格率Yij可以表达为
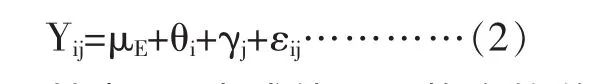
其中,μE为成绩不及格率的总平均值;θi、γj分别表示水平Ei和Dj的效应;εij为随机误差,服从N(0,σ2)分布;当然,此处的 εij的值与(1)中的值不同。 此时,要检验的原假设(仍用H01和H02表示)和对立假设(仍用H11和H12表示)分别为:
原假设:H01:θ1=θ2=0

对立假设:H11:θ1,θ2不全为 0

根据方差分析原理,对表3的数据进行方差分析,分析结果见表 4。 因为 FE(1,12)=4.67
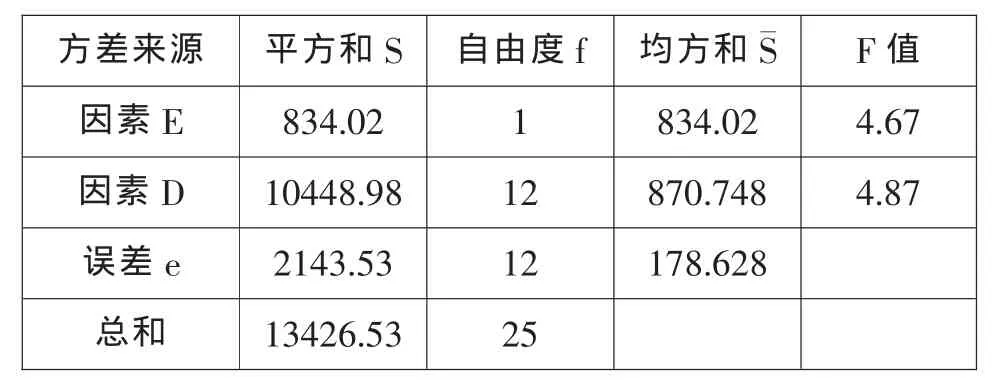
表4 成绩不及格率的方差分析表
三、其他课程的成绩统计分析
笔者还对这两个班级二年级时的专业基础课 《材料力学》和《结构力学》的考试成绩进行了统计分析(为节省篇幅,略去具体分析过程),分析结果表明,成绩的优良率和不及格率也都存在“组团式”的扎堆现象,只是F值比前述的F值小一些,这说明二年级学生的考试成绩与寝室的相关性比三年级时的相对弱一些。
之所以会出现以上的统计分析结果,笔者认为有如下的原因。新生入校后,都有一个新鲜、新奇、激动等的情绪不稳定期,这个时期学生管理工作者及任课教师的教育、引导,特别是管理就显得尤为重要,如果一个学生在一年级放纵了自己,那么他在后三年的学习中很难有理想的成绩及结果。新生经过一年级的情绪波动后,到二年级时,许多学生都要重新认识自我、重新自我定位,对专业、对人生、对未来也要重新思考,因此不同的学生作出了不同的选择:或努力拼搏,或按部就班,或放纵自己,或浑浑噩噩,所以到二年级时,学生的学习成绩就会出现两极分化,考试成绩也会出现“组团式”的扎堆现象,只是这些扎堆现象还不很稳定,同时这种扎堆现象与寝室的相关性还达不到三年级时的相关程度。到三年级时,基本上每个学生的学习情况都稳定了,选用大三学生的学习成绩进行统计分析具有稳定性和真实性。
四、结果与讨论
目前在大学校园里存在两种形式的考试成绩扎堆现象,对“散发式”的、集中在某些少数学生身上的考试成绩扎堆现象,很容易通过对照考试成绩册发现和判断。对这种形式的扎堆现象,特别是不及格情况的扎堆现象,教师及管理者首先要了解情况,摸清原因,有针对性地做学生的工作,并寻找相应的解决办法。
对以寝室为单位的 “组团式”的考试成绩扎堆现象,需用数理统计的原理进行分析后,才能判断。由统计分析结果看出,不论是学习成绩的优良率还是不及格率,都与寝室显著相关,而与课程门类无关。同时还可以看出,成绩优良率和不及格率与寝室的相关性不相同。因为不及格率的 F 值 FD(12,12)=4.87>F0.01(12,12)=4.16,因此不及格率与寝室的相关性非常显著。出现这一现象的原因只能是室风造成的。这一结果提醒学生管理工作者,对二年级、三年级的学生,每年都要进行专业课成绩的统计分析,在每学年学生寝室南北向调换时将不及格率集中的寝室内的学生分散到优良率集中的寝室中(说明:我校的学生寝楼均为南北两面布置寝室的结构形式,为了让住在寝楼的阳面和阴面的学生都有“享受阳光”的均等机会,每一学年都要进行南、北面寝室学生的调换)。因为,人们都有从众心理,当一个寝室内的6个学生中有5个学生都努力学习,剩下一个学生他不好意思不好好学习。相反当一个寝室内的6个学生中有5个学生都不好好学习,剩下一个学生他努力学习时反而会不好意思。
由前面的分析看出,重视对学生的过程管理,比重视目标管理将更有效[4],因为,不同的过程管理,一定会有不同的结果。
[1]熊瑞生.注重过程管理与质量的钢结构课程设计的改革与实践[J].河南广播电视大学学报,2013,26(3).
[2]庄楚强,吴亚森.应用数理统计基础[M].广州:华南理工大学出版社,1992.
[3]盛承懋,楼江,余晓红.统计学[M].南京:东南大学出版社,2009.
[4]熊瑞生.期中考试的形式与内容的改革与实践[J].宜春学院学报,2012,34(8).
