基于支路两端母线频差的失步解列判据研究
2014-10-18陈恩泽刘涤尘廖清芬张洁琼
陈恩泽,刘涤尘,廖清芬,张洁琼
(武汉大学 电气工程学院,湖北 武汉 430072)
0 引言
近年来,世界各国大面积停电事故[1-2]屡有发生,研究表明大停电事故的发生往往是由于电网互联规模的扩大,所产生的局部扰动通过联络线扩散至整个电网导致的[3-5]。失步解列作为电网的第三道防线,是消除电网振荡和防止大面积停电的重要措施[6-9]。
失步解列判据是以电网失步振荡过程中的电气量变化特点为研究基础,总结归纳出的基于单个或多个电气量的判断电网失步特征的方法,要求在电网发生各种异常状态时能够准确地判断电网的失步状态。现有的失步解列判据主要分为4类:第1类是间接反映功角的判据[10-12],如阻抗型失步解列判据,电流型失步解列判据,电压型失步解列判据,基于相位角的失步解列判据,基于有功功率、无功功率的失步解列判据等;第2类是反映能量的判据[13];第3类是基于直接测量两侧电压相角差的失步解列判据[10];第4类则是根据电网特点,结合各个判据的优势所形成的复合判据[14]。
现有解列判据的整定多基于就地量测量,仅能反映一类或几类失步特性,存在不够完善、协调配合等问题。前期研究发现,受电网运行方式、故障形式的影响,判据的适应性显得非常重要,尤其是当振荡中心发生迁移时,准确判断失步状态并实施解列对于电网安全稳定具有重要意义。如仿真发现有的振荡中心所在支路ucos φ轨迹只穿过2个区域;测量点相位角在0~360°内变化,只能提供方向信息;当振荡中心在相邻2条线路上快速来回迁移时,基于无功功率积分的判据受限于振荡周期很短而无法计算。
鉴于此,本文依据等频差原则[15]推导了等值两机系统异步运行时电压的变化特点,依据失步中心出现频率与两端系统频差的对应关系提出基于支路两端母线频差的失步解列判据,以CEPRI 36节点系统为例,通过设置单一严重故障,分别在固定振荡中心和振荡中心发生迁移2种情况下对本文所提判据进行验证,并与实际解列装置所采用的判据进行比较。
1 异步运行时的电压变化
国内外已有研究表明,当电网受到故障的影响,2组机群间形成了失步振荡,可以依据失步断面将整个电网等值成两机系统进行研究。当电网异步运行时,电压、电流、频率、有功、无功等电气量均会发生变化。为了研究需要,可以认为在很短的时间内,失步振荡是一个相对稳定的过程,假设计算时段内各个系统频率不变,即等频差[15],并作如下假设:
a.用一个幅值固定的简单电动势源表示等值发电机;
b.系统中的阻抗角φeq都相等;
c.在频率实际可变化的范围内,认为线路整体阻抗Zeq恒定;
d.不考虑中间负荷的影响。
如图1所示的等值两机系统模型,两等值发电机电动势为EM和EN;发电机内部阻抗归算在线路上,则线路整体阻抗Zeq由ZM、ZN和ZL组成;规定联络线电流方向为从M流向N。

图1 等值两机系统Fig.1 Equivalent two-generator system
两端电势表示如下:

其中,ωM、ωN分别为两侧等值机 GM、GN的角频率;EM、EN分别为 EM、EN幅值。
设基准点N端到联络线任意一点的阻抗为ZD,则联络线上任意一点电压瞬时值可以表示为:


将式(1)代入式(3)推导可得:

由式(4)可以看出,联络线上电压eD的影响变量分别有 ωN、Δω=ωM-ωN、ke、t、k。ωN反映的是异步运行电压的周期,一般接近于工频;Δω反映的是异步运行电压包络线的周期;ke反映了异步运行电压的幅值;k则反映了联络线上测量点的位置。
2 基于两端母线频差的失步解列判据
由式(4)可看出,两侧等值系统的频率差ωM-ωN就是电压包络线的频率。异步运行时电压包络线幅值在一个振荡周期里存在最大值和最小值,分别为:

每个振荡周期内,电压包络线幅值会在两侧功角差为0或2π时达到最大值,两侧功角差为π时达到最小值,由失步中心电压为零,即1-k-kke=0,可知失步中心位置 k=1/(1+ke),当ke为一定值时,失步中心位置唯一,并且两侧等值系统的频差为失步中心出现的频率。但是实际系统异步运行时,电压、频率不断变化,因此失步中心的位置也不断变化,但在两侧等值功角差为π,即失步中心出现的时刻,该时刻的两侧系统频差代表了失步中心出现的频率,由失步振荡的特性决定了这一时刻存在频差极大值。
因此,近似使用支路两端母线频差Δω表示失步中心出现的时间间隔,由于失步振荡是一个较快的过程,其频率较大,所以可以用两侧频率差的大小进行失步状态的检测。
基于支路两端母线频差的失步解列判据表达式为:

其中,Δωt0为当两端功角差为π时的两端母线频差,在实际应用中,用支路两端母线频差极大值来近似表示;Δωset可以根据实际电网的特性分析、统计数据、实际运行经验进行具体整定[10],本文通过对CEPRI 36 节点系统进行故障扫描,定为 0.1 p.u.(基准值为50 Hz)。
关于频差定值说明如下。
a.振荡中心迁移的影响。前期研究发现,当电网故障处理不及时或发生连锁故障导致电网稳定性受到严重破坏时[16],电网可能发生振荡中心迁移现象。此时由于电网失步周期较短和振荡中心的迁移变化,可能导致传统的失步解列判据失效,而基于支路两端母线频差的失步解列判据则不受上述因素影响,可准确判断并定位,为现有判据提供有力的支撑。
b.与现有判据的协调配合。电网一般将失步解列装置安装在省间联络线,且采用多套装置进行协调配合。以南瑞RCS-993A型失步解列装置为例,该装置采用阻抗循序判别方式进行失步判别和保护区域限制,为保证安全性,规定其失步继电器的快跳段可以测量200 ms以上的失步周期,在测量到失步后的第1个周期出口跳闸,失步继电器的慢跳段可以测量100 ms以上的失步周期,慢跳段可以整定在失步后2~15个周期后出口跳闸。可以看出,失步周期在200 ms以上时,解列装置有较好的稳定性。但失步周期在200 ms以下时,周期越短,对装置的影响越大,而本文所提判据可以和该装置相互配合,为失步周期在200 ms以下的解列控制提供依据,并在失步后的1个周期内发出动作命令。
3 基于支路两端母线频差的失步解列步骤
步骤1设定频差阈值Δωset,实时获取支路两端母线频率 ωi和 ωj,计算频差,计算步长为tstep。
步骤2当计算至ti+tstep时刻,若检测到支路两端母线频差出现极大值判断是否成立,并根据判断结果选择以下步骤。
步骤3判断此时确定的振荡中心所在支路是否符合可行解列断面,如果符合,则执行步骤4;否则,解列不动作,所有判断流程结束。
步骤4在ti+tstep+Δt时刻对振荡中心所在支路实施解列,其中Δt表示解列动作的整定延时。
判断流程见图2。关于可行解列断面说明如下。
a.随电网互联规模扩大,解列点由传统的一条线延伸为一个解列断面,可能由多条线组成,可行解列断面的关键特征在于可将系统分为2个独立部分。
b.传统的解列又称为被动解列,依据就地测量值进行判断,缺少全局信息的交换。研究发现,当振荡中心发生迁移时,在某一时刻,若振荡中心所处断面不满足可行解列断面,此时解列装置应可靠不动作;只有当振荡中心所处支路满足可行解列断面时,解列装置才应准确动作。

图2 判断流程图Fig.2 Flowchart of judgment
4 算例分析
以中国电科院CEPRI 36节点系统为例,其结构图如图3所示,仿真软件采用PSASP,计算步长0.01 s,频率基准值 50 Hz。

图3 CEPRI 36节点系统结构图Fig.3 Structure of CEPRI 36-bus system
4.1 振荡中心未迁移
在支路19-30处设置三相短路故障,0 s开始,持续0.4 s后系统发生功角失稳,其相对功角曲线(以G1为参考机组,G1为母线1所连机组,其他类似)如图4所示,可以看出G7、G8对其余机组功角失稳。

图4 发电机相对功角曲线Fig.4 Relative power angle curves of generators
观察所有线路两端电压相角差,如图5所示,只有支路19-30和33-34两端电压相角差在0°~360°内变化,且在180°处连续,所以振荡中心位于这2条支路上,而其他支路两端电压相角差则变化很小。

图5 线路两端母线电压相角差Fig.5 Bus voltage phase angle difference between two terminals
分别观测所有支路两端母线的频率(标幺值),选取支路 19-30、30-31、31-33、33-34 为例,见图6。
由图6可以看出,支路19-30和33-34作为振荡中心所在支路,其两端母线频差较大,而支路30-31、31-33两端母线频率基本一样,很好地证明了振荡中心所在支路和非振荡中心所在支路的区别。
以支路19-30两端母线频率为例,其频率差(标幺值)见图7,分别取时间段内的曲线,见表1、2。
由图7和表1可以看出,振荡中心所在支路两侧母线频差在单个周期内,存在一个极大值,当等值功角差达到180°时,频差最大;由表2可以看出,随着失步振荡过程的发展,频差逐渐增大,意味着振荡过程越来越剧烈。
根据所提供的时刻,分别对支路19-30、33-34在 t=1.11 s实施断线操作(实际解列时应根据所提供时刻进行调整,以避免开断电流过大),系统趋于稳定,任意选取一条支路,如支路14-19有功功率(标幺值)如图8所示,可以看出解列后功率变化趋于平稳。

图6 支路两端母线频率Fig.6 Bus frequency at two terminals

图7 支路19-30两侧母线频差Fig.7 Bus frequency difference of line 19-30

表1 支路19-30两侧母线频差Tab.1 Bus frequency difference of line 19-30

表2 功角差为180°时的母线频差Tab.2 Bus frequency difference when power angle difference is 180°

图8 支路14-19有功功率Fig.8 Active power of line 14-19
4.2 振荡中心迁移
在支路23-24处设置三相短路故障,0 s开始,持续0.8 s后系统发生功角失稳,其相对功角曲线如图9所示,可以看出1.2 s左右G1开始相对其他机组功角失稳,振荡过程中G2的相对功角则在不断地变化。

图9 发电机相对功角曲线Fig.9 Relative power angle curves of generators
观测支路两端母线电压相角差,如图10所示。观察图 10(a)、(b),可以发现振荡中心在支路 23-24、22-23 上迁移;观察图 10(c)、(d)同时发现振荡中心在支路9-22和9-24上迁移。
分别以实际失步解列装置所采用的基于ucos φ的失步解列判据和基于相位角的失步解列判据进行说明,受篇幅所限,仅给出部分示意图,如图11所示。
基于ucos φ的失步解列判据是根据ucos φ的变化区域进行失步状态的判别与振荡中心的定位,需要至少穿过4个区域才能定位为振荡中心。结合图 10,由图 11(a)可见,大概在 0.9~1.8 s时间段内,振荡中心位于支路22-23上,但是该时间段内,ucosφ的变化只穿过2个区域,不满足判据,表明该判据的动作区域整定存在问题;而基于相位角的失步解列判据则是根据相位角的变化区域进行失步状态的判别,该判据只能提供振荡中心所在方向。由图11(b)可以看出,由于振荡中心的快速迁移,使得相位角轨迹变化迅速,导致方向的判别与振荡中心的定位存在困难。

图10 支路两端母线电压相角差Fig.10 Bus voltage phase angle difference of two terminals

图11 ucosφ和相位角变化曲线Fig.11 Curves of ucosφ and phase angle
采用本文所提出的基于支路两端母线频差的解列判据,计算支路两端母线频差,比较频差极大值与阈值的大小关系,判断振荡中心所在支路,如表3和表4所示。

表3 支路22-23和23-24的|Δω|max,tiTab.3 |Δω|max,ti of line 22-23 and 23-24
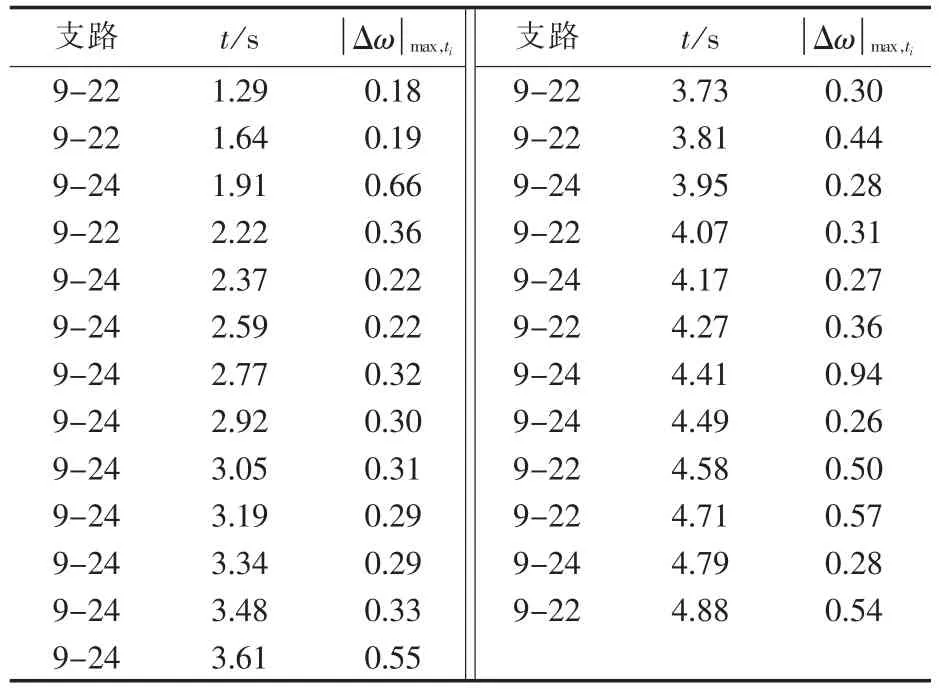
表4 支路9-22和9-24的 |Δω|max,tiTab.4 |Δω|max,ti of line 9-22 and 9-24
表3和表4明确给出了振荡中心分别在支路22-23、23-24和9-22、9-24来回迁移的情况以及相应的时间节点。观测发现在1.27 s、1.29 s、1.64 s振荡中心位于支路22-23、9-22上,但是该支路不满足可行的解列断面,因此解列应可靠不动作;而在1.92 s、1.91 s振荡中心位于支路23-24、9-24上,此时满足可行解列断面。
根据所得到的时间节点,在1.93 s+Δt,此处Δt=0.04 s,即在1.97 s(实际电网解列时可以根据具体电网的电压等级和解列装置的动作特性进行整定延时)对支路9-24和23-24实施解列。任选某一支路,观测其解列前后的支路有功功率(标幺值),如图12所示,可以看出实施解列后,振荡趋于平稳,证明了本文所提出的解列判据在振荡中心发生迁移时依然可以快速准确地判断失步状态、定位振荡中心,实施解列,有效地抑制了振荡。

图12 支路14-19有功功率Fig.12 Active power of line 14-19
由上述仿真结果可以发现,受振荡中心位置快速变化的影响,支路两端电压相角差快速变化,使得判断存在困难;基于ucos φ的解列判据,其曲线同样在快速地变化,且变化区域的整定对于判断结果影响较大;基于相位角的解列判据,由于只能提供方向性的判断结果,振荡中心位置的判断需要多条支路相互配合,计算量较大,由于曲线的快速变化,其变化规律的判断也存在一定的问题,上述判据的整定均需要1个失步周期。而本文所提出的基于支路两端母线频差的失步解列判据,只需要半个周期就能给出判断结果,时效性好,计算简单方便,计算量小。
5 结论
本文以等值两机系统中异步运行电压变化规律为理论基础,依据等值系统频率差反映了失步状态下失步中心出现频率的特点,提出了基于支路两端母线频率差的失步解列判据。
a.该判据仅需测量母线频率,进行简单的减法运算,可以实时判断系统的失步运行状态,准确定位振荡中心,不需要复杂的系统等值。
b.可以在电网第1个失步振荡周期内就发出解列信号,具有良好的时效性;可以提供相应的时间节点,为失步断面的解列装置协调配合提供了依据,同时通过整定延时就可以避免断路器开断电流过大所造成的危害。
c.可以准确区分短路故障、同步振荡、异步振荡,不受电网运行方式、故障形式的影响,即使发生振荡中心迁移,也可以快速准确地判断失步状态,定位振荡中心,保障了电网的安全稳定。
