纯铝弯曲的单晶体塑性有限元模拟

王 琦，黄庆学，马立东

(太原科技大学材料科学与工程学院，太原 030024)

随着计算机科学技术的发展，计算机仿真技术的日趋成熟，以及可视化工具的出现，材料细观角度的有限元模拟已经成为研究的热点。从晶体塑性理论出发建立晶体塑性模型，并将晶体塑性模型有限元结合，即晶体塑性有限元(Crystal Plasticity Finite Element Method，CPFEM)，从细观方面了解材料的变形机理从而能更好的把握材料的宏观性能，对强化材料，指导材料的塑性加工，塑性成型具有更为重要的意义。本文通过晶体塑性有限元的方法对铝板弯曲过程晶粒的滑移和变形过程进行了有限元模拟。

由Hill和Rice提出[1-3]最初的CPFEM基础理论，主要依据的是晶体塑性变形的Schmid定律。后来研究人员又提出了完整的率相关材料本构理论，其将单晶体塑性变形的产生归结于特定滑移系上的位错运动，将自硬化和潜在硬化速率引入到晶体塑性本构关系中，对相同滑移系和不同滑移系上位

错的相互作用进行描述。在国内晶体塑性理论和研究应用方面起步较晚，虽然如此，但是国内研究人员到目前为止也做了许多有意义的工作。例如，1997年，董湘怀等[4-6]开发了基于晶体塑性理论的板料成形过程的动力显式有限元分析程序，对单晶体和多晶体的塑性失稳以及织构对板材成形性能的影响进行了深入地研究。冯露等[7]通过ABAQUS/STANDARD用户材料接口UMAT做了对材料本构关系的分析，提出了对单晶体粘塑性滑移本构关系的一种求解方法，能够计算非线性变形的单晶体本构模型。

本文主要通过单晶体的塑性有限元理论开发纯铝单晶体材料用户子程序，结合ABAQUS有限元的子程序接口UMAT对子程序调用，计算铝板在不同压下位移的情况下不同滑移系的滑移启动情况及材料应变的不均匀性。

1 单晶体塑性本构理论

假设滑移变形不影响弹性性质，由Hill和Rice提出的基础理论可知单晶体弹性本构为:

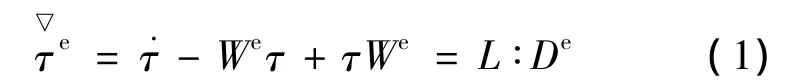
晶体继续变形进而产生塑性变形后，基于W的刚性导数为:

式中:W——旋转率张量

由公式(1)和式(2)得到:

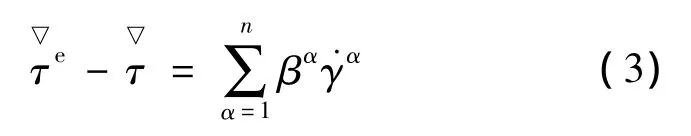
其中:

由(1)和式(3)的到单晶体本构方程:

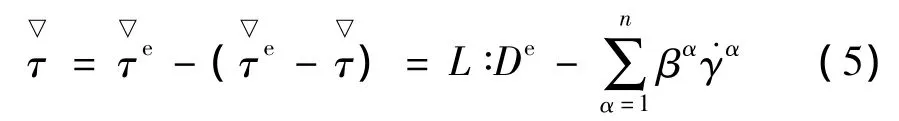
对于率相关滑移，第α个滑移系上的塑性剪切率和分剪切应力有如下关系:

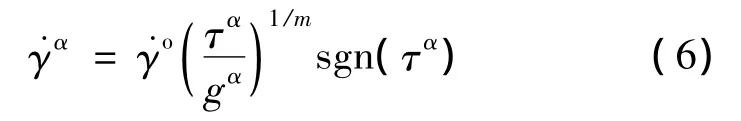
τα——第α个滑移系上的分切应力;

gα—— 硬化函数;

m——滑移系应变率敏感系数。

立方晶系中，单晶体滑移系的硬化规律可表示为:

式中:hαβ——表示硬化模量矩阵，其为 γ的函数:

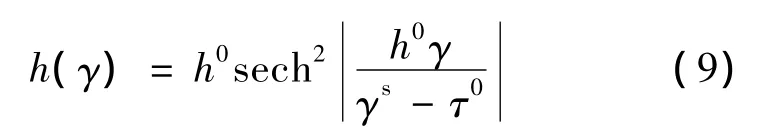
式中:h0——初始硬化率;

γ0—— 屈服切应力;

τs——流动应力饱和值;

q—— 硬化比率。

2 铝板弯曲模拟过程及结论

2.1 弯曲模拟及变形的分析

模拟过程的积分方法是由Kalidindi所给出的[7]，通过有限元软件ABAQUS的材料用户子程序接口UMAT将晶体塑性理论的本构模型嵌入到有限元软件ABAQUS中，进行了对铝板的弯曲过程模拟。模拟试件采用二维模型，其尺寸为长30 mm，高为1 mm.模拟过程用到的材料参数[8]为:

C11=108000 MPa，C12=62000 MPa，C44=28300 MPa，硬化比 q=1.4，其他参数参考文献[8]，参考剪切应变率=0.001，初始硬化率h0=60 MPa，屈服切应力 τ0=21.17 MPa，流动应力饱和值 τs=61 MPa.

几何模型建模时，支撑棍和压下棍定义为刚体，铝板定义为变形体300 mm×10 mm的长方形铝板，在变形体铝板两边距离端点5 mm处设置全约束。建立的弯曲几何模型如图1.

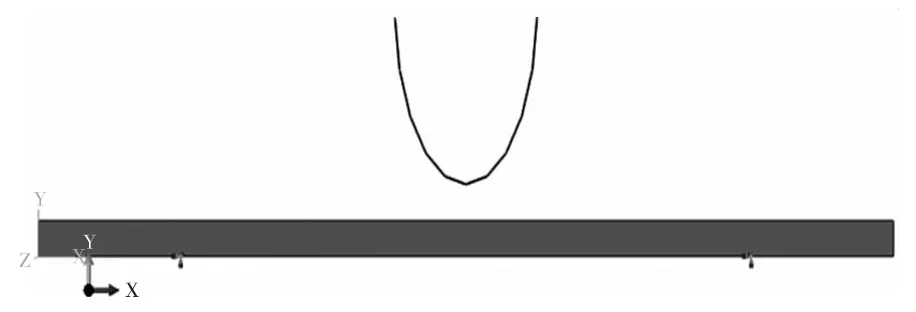
图1 弯曲几何模型Fig.1 Curved geometry model

计算过程中计算速度较快，计算比较稳定没有出现在计算过程中的不收敛现象。弯曲变形过程由弹性变形和塑性变形两部分组成。其中晶体的滑移引起塑性变形。在外力下，由于板带内部存在的应力而使滑移系存在分剪切应力，从而影响着滑移系的启动和滑移系应变的大小。下面主要从压下位移的不同对变形结果进行分析。

在几何模型建立时模型设置两个Step，第一个Step采用压下位移为20 mm，使压下辊先与板材刚好接触。在第二个Step中分别采用压下位移为30 mm，40 mm的方法对板材进行模拟。图2和图4是不同压下位移下的模型云图变化情况。

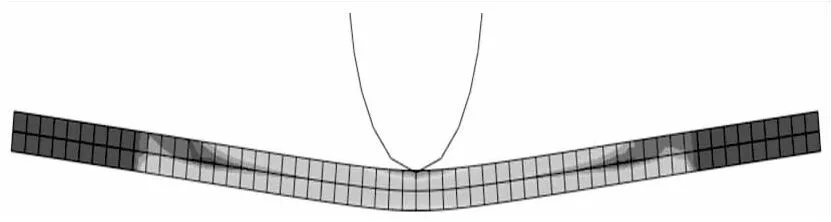
图2 下位移30 mm时的Mises应力云图Fig.2 Mises stress nephogram of displacement under 30 mm

图3 宏观条件下压下位移为30 mm的应力图Fig.3 Displacement for 30 mm macro conditions under the press stress diagram

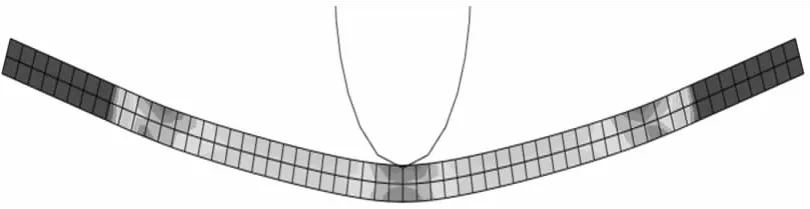
图4 下位移40 mm时的Mises应力云图Fig.4 Mises stress nephogram of displacement under 40 mm

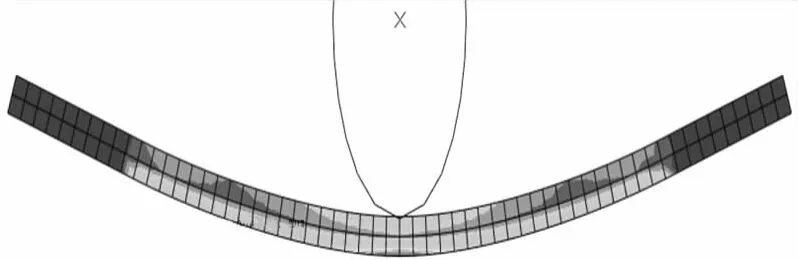
图5 宏条件下压下位移40 mm时的应力云图Fig.5 Displacement for 40 mm macro conditions under the press stress diagram

由图2和图4可以看出，当压下量为30 mm时应力分布比较均匀，只有在下压辊的接触部分铝板的中间应力变化较大。当压下量增加到40 mm时，板带的应变开始由中间向两端延生，在板带中间和两端的支撑点出都出现了较大的应力。由图3和图5对比可以看出这些非均匀的应力变化宏观模拟是难以实现的。由于晶体塑性理论从滑移的角度描述材料的塑性变形，因而可以很好的反映出材料变化的非均匀性。

2.2 滑移系启动分析

对于纯铝板属于面心立方晶体，对模拟过程的12个滑移系的启动进行了模拟结果数据采集，在INP文件中将frequency设置为2即每两步输出一次。本文通过建立的铝板材料子程序很好的模拟了在不同压下量的情况下的滑移系的启动情况，面心立方晶体具有12个滑移系，通过计算显示了10个滑移系的滑移系剪切应变情况，数据显示其中有(111)，[10-1]和(1-11)，[10-1]两套滑移系未启动，其滑移系剪切应变为0.图6和图7显示了在压下位移不同情况下启动的滑移系剪切应变随时间变化的情况。

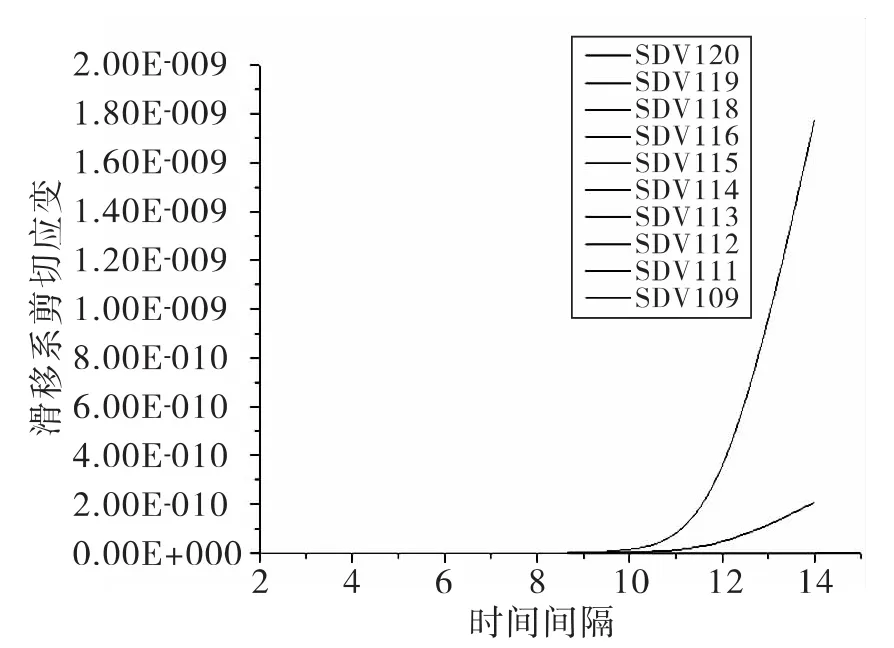
图6 压下30 mm时滑移系剪切应变随时间变化曲线Fig.6 Press down 30 mm slip system when shear strain curve over time

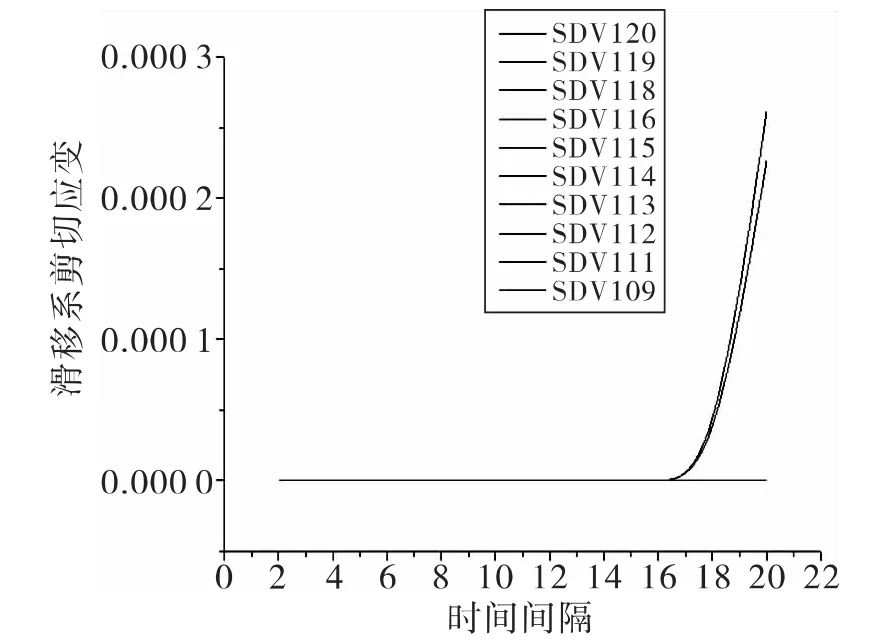
图7 压下40 mm时滑移系剪切应变随时间变化曲线Fig.7 Press down 30 mm slip system when shear strain curve over time

由两幅曲线图可以看出滑移系109和111应变值重合，滑移系115和116应变重合并且应变都较大，滑移系启动。其他滑移系应变值几乎为0.当压下位移由30 mm增大到40 mm时，滑移系109和111、115和116的应变值都相应的增大，而其他滑移系应变值增幅不明显仍接近于0.

3 结论

晶体塑性本构模型，应用ABAQUS用户材料子程序接口UMAT对材料模型进行调用，结合inp编写，很好的完成了对纯铝板弯曲过程变形情况的数值仿真。

(1)计算结果显示通过调用子程序进行细观方面模拟能很好的反映材料变形过程的不均匀性。压下位移不同，非均匀性变形程度不同，这与宏观条件下模拟结果对比可以发现以往宏观的模拟式难以实现的，这充分说明了单晶体材料模型能够很好的反映材料的各向异性。

(2)在变形过程中不同的压下位移影响着滑移系的启动，模拟结果表明不论压下位移多大，总有两套滑移系并未启动，说明未启动的滑移系取向因子处于硬位相，不产生滑移。而启动的滑移系也随着压下位移及加载取向的不同而不同。

上述研究通过计算机模拟仿真进行了深入的探索，在细观方面表征材料塑性变形不均匀性、滑移系启动情况更能真实的反映材料的变形情况。

[1]HILL R，RICE J R.Constitutive analysis of elastic-Plastic crystals at arbitrary strain[J].J Meeh Phys Solids，1972，20:401-413.

[2]ASARO R J，RICE J R.Strain localization in ductile single crystal[J].J Mech Phys Solids，1977，25:309-338.

[3]ASARO R J.Crystal plasticity[J].J App Mech，1983，50:921-934.

[4]董湘怀.金属塑性变形中织构演化的计算机模拟[J].塑性工程学报，1998，5(3):8-14.

[5]董湘怀，仲盯英治.晶体塑性模型在板材成形计算机模拟中的应用[J].中国机械工程，1997，8(4):27-30.

[6]郑莹，董湘怀，李志刚.晶体方位对板料成形制耳的影响[J].中国机械工程，2001，12(9):1070-1072.

[7]KALIDINDI S R，BRONKHORST C A，ANAND L.Crystallographic texture evolution in bulk deformation processing of FCC metals[J].Journal of the Mechanics and Physics of Solids，1992.40，537-569.

[8]ROTERS F，WANG Y，KUO JC，et al.Comparison of single crystal simple shear deformation experiments with crystal plasticity finite element simulations[J].Adv Eng Mat er，2004，6:653.