一种求解不定信赖域子问题的精确解法

于海波，王希云，李 亮(太原科技大学应用科学学院，太原 030024)

信赖域方法的关键是每次迭代时都需求解下面形式的信赖域子问题：

(1)

其中g∈Rn为目标函数在当前迭代点的梯度，B∈Rn×n为目标函数在当前迭代点的Hessian矩阵或其近似，△∈R为信赖域半径，δ∈Rn为待求变量。当△变化时，上述信赖域子问题(1)的解δ*就形成一条空间曲线，称为最优曲线[1]。

求解信赖域子问题的方法主要有精确求解法、折线法和截断共轭梯度法.其中折线法是比较有效和实用的方法，如单折线法、双折线法[1]、切线单折线法、不定折线法、混合折线法、双割线折线法等[2-5]。而目前常用的精确求解法主要是牛顿法，为避免牛顿法中初始迭代点位置选取的困难，李亮[6]在Hessian阵正定的前提下提出了一种解信赖域子问题的分段割线法，有效避免了牛顿法中初值选取的困难，提高了计算效率。本文在此基础上，针对Hessian阵不定的情况，提出了一种求解信赖域子问题的修正分段割线算法，进一步完善了这一精确求解方法在一般二次模型中的应用。

1 分段割线法的思想

基于信赖域子问题精确求解方法的思想，得到最优曲线的参数方程如下[6]：

δ=-(B+μI)-1g(μ>0)

(2)

定义函数y=f(μ)=‖δ‖2=‖-(B+μI)-1g‖2，(μ≥0).则信赖域子问题(1)的解δ*就是：当μ=0时，解δ*=-B-1g；当μ>0时，通过求解一元非线性方程f(μ)-△=‖-(B+μI)-1g‖2-△=0得到解μ*，此时解δ*=-(B+μ*I)-1g.

分段割线法的思想是在B正定的前提下，利用函数f(μ)的单调减性，当给定的信赖域半径△≥‖B-1g‖2时，令μ=μ0=0，得到子问题的最优解δ*=-B-1g；给定的信赖域半径△<‖B-1g‖2时，以给定的步长不断增大μ，从而缩小函数f(μ)的值，最终找到一个最小的正整数m，使得f(μm)-△≤0，得到方程f(μ)-△=0的有根区间[0,μm].记节点μk处的函数值f(μk)为yk，k=0,1,…,m,通过对节点(μk,yk)，(k=0,1,…,m)进行线性插值构造m条直线，连接所有直线构成分段割线，最后在插值点(μm-1,ym-1)和(μm,ym)之间利用线性插值构造的线性函数代替f(μ)来求解方程f(μ)-△=0的根μ*，从而求得子问题的解δ*=-(B+μ*I)-1g.

2 不定矩阵的修正

上述分段割线法是在B正定的前提下提出的，若B不定，则二次模型(1)不一定有极小值点，甚至没有平稳点[1]。为了克服这些困难，通常采用强迫矩阵正定的方法。文中采用了两种修正不定矩阵B的方法，一种是利用Bunch-Parlett分解和矩阵的特征值来构造新的对称正定矩阵G[2]；另一种是利用Gill-Murray提出的修改Cholesky分解来修正不定矩阵B[1]，从而提出了两种解决不定信赖域子问题的修正分段割线算法。通过数值实验比较了利用两种修正方法解不定子问题(1)的最优解。

2.1 Bunch-Parlett分解

对实对称矩阵B进行Bunch-Parlett分解：

RBRT=LDLT

其中R为置换阵，L是单位下三角矩阵，D为一块对角阵，对角块的阶数为1或2.为方便计算，不妨设置换阵R=I，其中I为单位矩阵。从而上式变为：

B=LDLT

由于矩阵D和B具有相同的惯性，即它们具有相同数目的正特征值、零特征值和负特征值[7]，本文利用D的特征值来构造对称正定矩阵G.

不妨记D的特征值为λ1,λ2,…,λn，对应于特征值λ1,λ2,…,λn的特征向量为p1,p2,…,pn，令P=(p1,p2,…,pn)T，下面分λi>0，i=1,2,…,n和存在i使λi≤0两种情况来构造正定矩阵G.

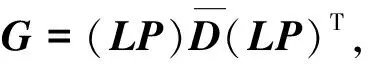
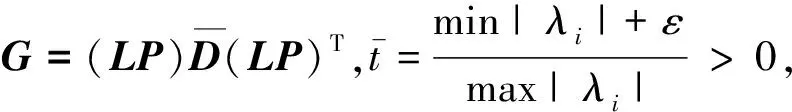
由文献[4]可知，G是对称正定阵且-Gg是拟牛顿方向。

2.2 修改Cholesky分解

采用文献[1]中Gill-Murray提出的修改Cholesky分解对不定矩阵B进行修正。

3 修正分段割线算法

下面给出该算法的具体步骤：

步0给定梯度g，不定矩阵B，信赖域半径△，步长h.

步1取调整参数ε=0.1(或ε=1.1)，对B进行Bunch-Parlett分解[7]，得到B=LDLT，利用D的特征值来构造对称正定矩阵G，令B=G-1；

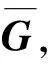
步3计算f(μk)，μk=kh，令yk=f(μk).在插值节点(μk-1,yk-1)和(μk,yk)之间用线性插值方法构造直线Lk(μ)，形成修正分段割线Γ.

注：步0中选取的步长h越小，则由该算法求得的信赖域子问题的最优解δ*越精确。

4 数值结果

对于无约束优化的信赖域子问题(1)，本文选取不同的信赖域半径△，利用测试函数Function 1和Function 2，分别测试了以上两种不定修正分段割线算法。其中q(δ)表示测试函数最优解的函数值，BPD表示采用Bunch-Parlett分解和矩阵的特征值的信息来修正不定矩阵的修正算法，CHD表示采用修改Cholesky方法修正不定矩阵的修正算法，HD表示文献[2]的混合折线算法。qCHD-qBPD表示分别采用CHD和BPD修正方法所得到的最优解的差值，该差值越大，说明采用BPD方法的修正分段割线法越好；qHD-qBPD表示分别采用HD和BPD方法得到的最优解的差值。具体数值结果见表1、表2及表3.

当选取不同的信赖域半径△来求解子问题(1)时，分析表1和表2可以看出，当信赖域半径相对较小时，采用CHD方法的修正分段割线法与采用BPD方法的修正分段割线法相比，CHD的结果要略优于BPD的且与精确解十分接近。然而随着信赖域半径的增大，CHD方法逐渐达到局部最优解并趋于稳定，采用BPD方法求得的最优解要优于CHD方法得到的最优解。

综上所述，虽然采用CHD方法在小半径下求解时精度较高，但是随着半径的增大，求解过程容易陷入局部最优的境地；对于BPD方法，求解过程比较稳定，而且可以得到相应半径下的全局最优解。为此，我们选取BPD方法来求解子问题(1)，并与HD算法进行比较。对比表3的数值结果可以看出，采用BPD方法求解子问题(1)得到的最优值明显优于运用HD算法得到的最优值。由此可见，修正分段割线法是一种求解不定信赖域子问题的很好的方法。

其中测试函数Function 1的拟牛顿步‖Gg‖=22.398，测试函数Function 2的拟牛顿步‖Gg‖=36.23.

其中测试函数如下：

表1 数值结果

表2 数值结果

表3 数值结果

参考文献：

[1] 袁亚湘，孙文瑜.最优化理论与方法[M].北京：科学出版社，2010.

[2] 赵丹.解信赖域子问题的混合折线法[J].徐州师范大学学报：自然科学版，2009，27(3)：38-41.

[3] 赵英良，徐成贤.解信赖域子问题的切线单折线法[J].数值计算与计算机应用，2000，21(1)：77-80.

[4] CHEN JUN，SUN WENYU.Nonmonotone Adaptive Trust Region Algorithms with Inde-finite Dogleg Path for Unconstrained Minimization[J].Northeast Math ，2008，24(1)：19-30.

[5] 王希云，邵安.一种双割线折法求解线信赖域子问题[J].应用数学，2012，25(2)：419-424.

[6] 李亮，王希云.解信赖域子问题的分段割线法[J].太原科技大学学报，2013，34(5)：393-397.

[7] 徐成贤，陈志平，李乃成.近代优化方法[M].北京：科学出版社，2002.

[8] 李董辉，童小娇，万中.数值最优化算法与理论[M].北京：科学出版社，2010.

[9] 任玉杰.数值分析及其MATLAB实现[M].北京：高等教育出版社，2007.

[10] 王建宏，钱峰.基于最速下降曲线的特征值法[J].南通大学学报：自然科学版，2007，6(1)：20-22.