基于无源性的分数阶控制在起重机防摆中应用

高武龙，陈志梅，孟文俊(.太原科技大学电子信息工程学院，太原 03004；.太原科技大学机械工程学院，太原 03004)

起重机作业过程中，一方面要求系统快速响应，实现小车定位，满足运送货物的要求；另一方面，运送过程中需有效地抑制负载的摆动，使其尽量小，且到达目的地后迅速衰减为零，避免与周围环境碰撞[1]。对于防摆问题，Nowacki Z[2]很早就利用PD控制器进行了研究，不过，其线性化的设计结构简单，但却使桥式起重机系统丧失了一部分非线性特性。目前很多研究[3-4]，往往依赖于精确的模型、复杂的算法，或只能在理想条件实现，而在有外来摄动和摩擦的情况下较难实现，控制器的鲁棒性不强。无源控制方法早期多用于机器人控制，后经Ortega等学者引入到电机控制中，因其从系统的能量入手，能够简化控制器，特别是在鲁棒性方面有较优异的性能，近年来得到了广泛的研究。方勇纯[5]、苏晴等[6]人在无源性分析的基础上，为保证系统所有状态渐近收敛，对系统控制Lyapunov能量函数(CLF)的势能项进行了修改，所设计的PD反馈控制能实现较快的收敛和一定的鲁棒性。遗憾的是他们都是在理想的条件下实现的，而且尽管基于无源性，PD控制却难以兼顾稳定性和快速性，鲁棒性也不强，易出现振荡现象和静态误差，降低系统的稳定性[7]。文献[8]中方勇纯等人为更进一步实现防摆效果，取控制Lyapunov函数为系统能量的平方，设计了一个非线性的控制器，该方法使得摆动次数减少一些，不过摆角仍稍显大，且对鲁棒性未做深入研究。

本文将分析系统的无源性，在构造控制Lyapunov能量函数基础上，结合分数阶微分方法，设计出基于无源性的分数阶控制器，实现存在摩擦及外界干扰等环境下，小车的精确定位和负载的有效防摆。并研究最佳的分数阶阶次区间、控制器的鲁棒性与稳定性。

1 系统动力学模型

如图1为桥式起重机的小车-负载二维模型，其描述的小车-负载动态方程为[9]：

(1)

式中，m为负载质量，M为小车质量，l为绳长，x为水平位移，θ为负载摆角，g为重力加速度，μx、μl为别水平运动和提升运动时摩擦系数，fx、fl分别为小车水平驱动力和负载提升力。利用欧拉-拉格朗日(Euler-Lagrange)方程，通过计算系统的能量建立动力学模型是常见的方法。则式(1)可改写成如下矩阵形式：

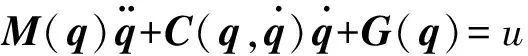
(2)

图1 桥式起重机的小车-负载模型

则系统状态:

q=(xlθ)T

(3)

惯量矩阵:

(4)

向心-柯氏力矩阵:

(5)

重力因子:

G(q)=(0 -mgcosθmglsinθ)T

(6)

控制输入:

u=(fxfl0)T

(7)

需要指出的几个系统性质是：

(1)由于系统控制输入量为二维而系统广义变量为三维，且受到一些非线性因素，如，饱和特性、继电特性等的影响，桥式起重机系统呈欠驱动性和非线性；

2 系统无源性分析

无源控制理论从能量角度来分析系统性能，根据其定义，当系统是耗散的，若供给率等于系统的输入与输出之积，则该系统是无源的[10]。若系统是无源的，则通过适当的输出反馈能够实现系统的镇定控制，使得闭环系统渐近稳定，因此，对于桥式起重机这类非线性系统，无源性是研究其稳定的一个重要特性。

系统总能量为：

(8)

其中，∂P(q)/∂q=G(q).

对式(8)求导，得：

(9)

(10)

3 控制器设计

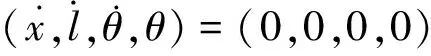
Hc=λHH+PTΛp=λHH+λx(x(δ))2+λl(l(δ))2

(11)

其中，Λ=dig(λx,λl,0);λH,λx,λl≥0.

对式(11)进行求导得:

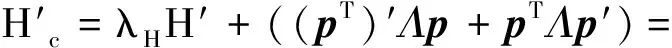
(12)

令γ=2δ，则:

(13)

取如下控制律:

(14)

整理得:

(15)

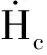
4 仿真研究

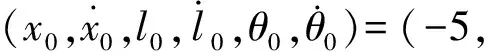
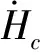
进一步缩小γ的范围，选取γ∈(-0.1,0.1)进行比较研究。在图4中，相比γ∈(0.01,0.1)，当γ∈(-0.1,-0.01)时，能量函数Hc能够在更短的时间衰减到0.不过，如图5所示，当γ≤0，位移曲线存在超调量，使得系统的定位效果不好。

图2 0<γ<0.5时能量变化

图3 -0.5<γ<0时能量变化

图4 -0.1<γ<0.1时能量变化

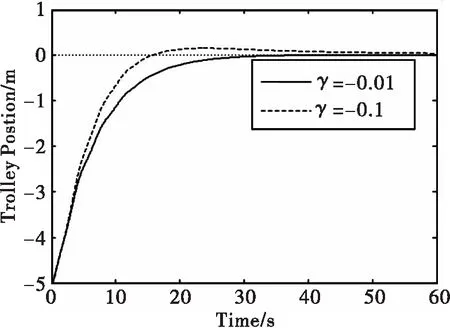
图5γ<0时小车位移

Fig.5Trolleyposition(γ<0)

图6 小车位移

图8 负载摆角曲线1

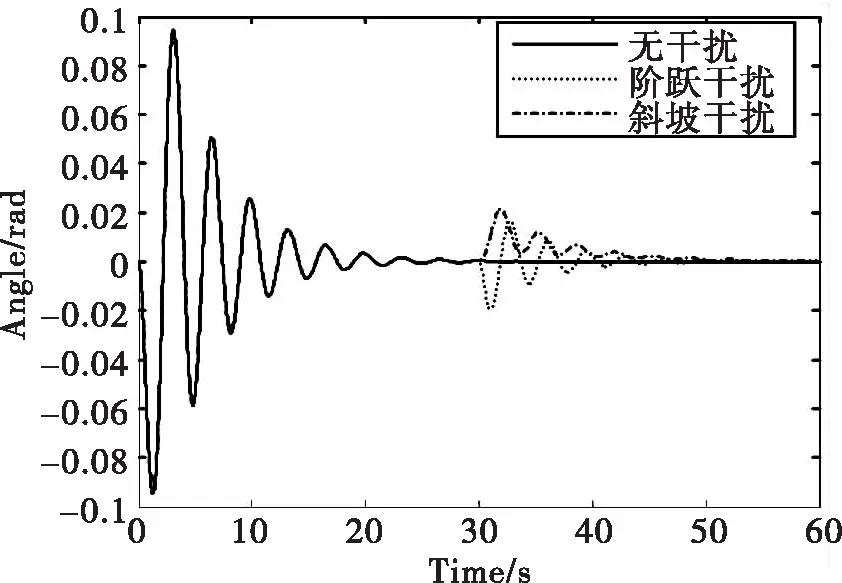
图10 负载摆角曲线3

当γ=0时，控制器将会变成一个无源PD控制器，选择γ=0.01设计的分数阶控制器与其进行比较研究，其仿真结果如图6-图8所示。由图6-图8，可以发现，尽管PD控制器小车速度和绳长变化速度稍快、摆动次数也少一些，不过，绳长却定位不准，摆角也明显更大。反观分数阶控制器，小车在40 s内到达了期望的位置，仅比PD控制器慢3 s，然而，却在10 s左右完成提升动作，绳长准确变为期望的3 m，整个过程摆动的次数不多，几乎呈谐振，摆角控制在(-0.1rad，0.1rad)以内，并在t=25 s时实现“零摆”。由此可见，本文设计的分数阶控制器改善了PD控制的性能，使得系统快速收敛而且准确。

而对存在摩擦和外界干扰的情况下的系统的鲁棒性和稳定性进行的研究，仿真结果如图9-图10所示。可发现，有阻尼状态下比无阻尼状态(即μx=μl=0)时的摆动稍微小一些，不过都在(-0.1rad，0.1rad)以内，说明控制器能有效地抑制摩擦的影响。而图10中，在t=30 s时对系统所加R=1的阶跃干扰和斜率k=-0.5的斜坡干扰，使得摆角在(-0.02rad，0.02rad)以内小幅振荡，并在15 s内迅速消除。由此可见，系统有着良好的稳定性和强鲁棒性。

5 结论

本文在系统无源性分析的基础上，修改了系统的控制Lyapunov能量函数，改造传统的PD控制器，设计了无源分数阶控制器。该控制器实现了小车的精确定位和负载的有效防摆，确保了系统的稳定，提高了系统的鲁棒性和快速性等性能。理论分析和仿真结果表明，无源控制理论和分数阶微分方法的有效结合应用于桥式起重机的防摆中，能取得良好的效果。

参考文献：

[1] CHOI S G，LEE H H.An anti-swing control of a 3-dimensional overhead crane[C]∥Proceedings of the 2000 IEEE American Control Conference，Illinois，USA，2000：1037-1041.

[2] NOWACKI Z，OWEZARZ D.On the roustness of fuzzy control of an overhead crane [C]∥Proceedings of the IEEE international Symposium on industrial Electronics，Warsaw，Poland，1996，61(5)：433-437.

[3] 杨斌，刘惠康，代文蕤.桥式起重机防摆控制器的设计[J].制造业自动化，2012，34(1)：122-124.

[4] XU W，GU W.Anti-swing control of a new container crane with fuzzy uncertainties compensation[C]∥Proceedings of the 2011 IEEE International Conference on Fuzzy Systems，Taiwan，Taipei，2011：474-478.

[5] FANG Y，DIXON W，DAWSON D，et al.Nonlinear coupling control laws for an overhead crane system[C]∥Proceedings of the 2001 IEEE International Conference on Control Applications，Mexico City，Mexico，2001：639-644.

[6] 苏晴，卢耀祖，张氢.岸边集装箱起重机防摇及定位控制研究[J].机电一体化，2008，2：51-54.

[7] 刘微容，李二超，李炜.机器人轨迹跟踪改进PD控制研究[J].2007，26(6)：89-91.

[8] FANG Y，DIXON W，DAWSON D，et al.Nonlinear coupling control laws for an underactuated overhead crane system [J].IEEE/ASME Transactions on Mechatronics，2003，8(3)：418-423.

[9] LEE H H，CHOI S G.A model-based anti-swing control of overhead cranes with high hoisting speeds[C]∥Proceedings of IEEE International Conference on Robotics and Automation，Seoul ，Korea，2001(1-4)：2547-2552.

[10] 王久和.无源控制理论及其应用[M].北京：电子工业出版社，2010.

[11] 李彭安，陈志梅，孟文俊，等.基于无源性的三维桥式起重机定位和防摆控制[J].太原科技大学学报，2013，34(3)：211-215.

[12] OUTALOUP A，LEVRON F，MATHIEU B，et al.Frequency-band complex noninteger differentiator?：characterization and synthesis[C]∥Proceedings of IEEE Transaction on Circuit and Systems-I：Fundamental Theory and Applications，2000，47(1)：25-39.