采用欧几里得贴近度的精密车削误差源模糊诊断方法

王建涛，顾立志，杜伟文，黄燕华，瞿少魁

（华侨大学 机电与自动化学院，福建 厦门361021）

机械加工过程是一个不断变化的极其复杂的过程，对零件加工精度有影响的因素很多，且各种影响因素与产品精度之间对应关系复杂，往往是非确定的、模糊的.机械加工误差直接影响零件的质量和使用性能，机械加工误差来源于加工系统各误差源.对误差源的恰当诊断，进而控制加工误差具有重要意义.由于误差源的多样性和随机性，对其诊断难度很大［1］.机械加工误差源的诊断方法主要有如下4种：1）基于启发式的诊断方法；2）基于进化计算的诊断方法［2-3］；3）基于专家系统的诊断方法［4-5］；4）基于模型的诊断方法［6］.模糊数学是研究和处理带有“模糊”性质的事物的一种理论和方法.它在工件误差与其误差源判别过程中，对于模糊信息和经验知识的数值化描述方面比其他方法具有很大的优势［7-8］.本研究提出基于模糊数学原理，采用欧几里得贴近度判别和确定加工误差源的方法，以揭示影响零件加工误差的主要误差源及其存在规律，进而找出减小加工误差、提升产品加工精度的途径.

1 模糊数学理论基础

1）模糊集合 .设U是论域，称映射μ∶U→［0，1］，u｜→μA（u）确定了U上的一个模糊子集，记为A，μA称为隶属函数，μA（u）在u＝u0的函数值称作u0对A的隶属度［9］.μA（u）的大小能够反映u对模糊子集A的从属程度，μA（u）的值愈接近1，表示u从属A的程度愈高，μA（u）的值愈接近0，表示u从属A的程度愈低.

2）模糊矩阵［10］.设U＝｛u1，u2，…，un｝，V＝｛v1，v2，…，vm｝，R为U到V的一个模糊关系，即R∈F（U×V）.则R可用一个m×n阶矩阵来表示，即R＝（ri，j）m×n，其中ri，j＝R（ui，uj），i＝1，2，…，m；j＝1，2，…，n.由于R（ui，uj）∈［0，1］，故称R＝（ri，j）m×n为模糊矩阵.

3）模糊集合间的贴近度［11］.考虑F（U）上的二元函数σ∶F（U）×F（U）→［0，1］，（A，B）→σ（A，B）.若满足下列3条公理：1）σ（A，A）＝1，σ（U，）＝0；2）σ（A，B）＝σ（B，A）；3）A⊆B⊆C⇒σ（A，B）∧σ（B，C）.则称σ为F（U）上的贴近度函数，σ（A，B）为A与B的贴近度.

在机械加工误差源的诊断中，工人对已加工工件的质量特征进行初步判断，对可能引起加工误差的误差源用模糊语言描述 .例如：该零件的圆度误差“非常大”、“一般大”、“比较小”，加工过程中工件受力变形“非常小”、“比较大”等.这些语言就构成了语言集合.

4）语言隶属度 .设论域U上的语言模糊子集A，可用如下一个映射μA（x）定义，即μA（x）∶U→L，x→μA（x）＝语言隶属度，其中L为模糊语言值集合，μA（x）为A的隶属函数，表示模糊语言元素x隶属于A的程度.

5）阈值原则 .设论域U＝｛u1，u2，…，un｝上有m个模糊子集A1，A2，…，Am，即m个模型.对于任一u0∈U，取定水平λ∈［0，1］，若存在i1，i2，…，ik，使得Ai，j（u0）≥λ，（j＝1，2，…，k），则判定为u0相对地隶属于Ai1∩Ai2∩…∩Aik.

对于语言模糊子集相互交叉（即边界模糊，有交叉现象），其对应的隶属函数目前只能基于领域专家学者的经验知识进行估算，无法用精确的数值模型计算的方法获取.经过反复仿真分析表明，使用7个定性词汇（即7个语言值如“很大”、“比较大”等）来描述模糊语言元素的隶属度，就可以满足使用要求.因此，可以定义该类情况的隶属函数，即μA（x）＝｛很大，相当大，比较大，中等，比较小，相当小，很小｝.

为满足模糊逻辑运算和模糊诊断的需要，用［0，1］上数值表示语言隶属度，即μA（x）＝｛1，5／6，4／6，3／6，2／6，1／6，0｝.通过这种方式及其表达，即可实现加工误差和加工误差源模糊信息的数值化.

2 加工误差与误差源的模糊数学表达

2.1 误差源的分类

机械加工误差源分类，如图1所示.分析机械加工工艺系统，对加工过程中存在的误差源进行分类.误差源的恰当分类有利于获取加工误差与误差源之间的映射关系［12］，便于利用模糊数学的方法描述加工过程中的现象和事实信息.

图1 误差源的分类Fig.1 Classification of error sources

2.2 加工误差与误差源之间的逻辑关系

1）不同误差源对加工误差的影响程度不同，即权重大小不同.由于加工误差具有误差敏感方向，在众多误差源中，只有某个别误差源作用在加工误差的敏感方向上，则其对加工误差的影响程度较大，即权重大；其他误差源作用在与加工误差敏感方向成一定角度的方向上，角度越大，对加工误差的影响程度越小，即权重小［13-14］.

2）不同误差源对同一个加工误差的影响方向不同，即有使加工误差变大的，有使其变小的.

3）同一误差源对不同加工误差的影响大小不同.

4）在机械加工工艺系统中，工件加工误差不但与各误差源的原始误差大小有关，而且还与原始误差的传递途径有关［15］.例如，机床主轴的回转误差对加工工件的直径及圆柱度有较大的影响，而主轴的轴向窜动对工件直径和圆柱度没有影响.

5）工艺系统的误差源与工件加工误差是多对多的对应关系.工件的某一项加工误差是由多个误差源综合作用引起的，而一个误差源也能够引起多项加工误差.如：机床主轴的回转误差一般可以导致被工件的圆柱度误差、圆度误差、表面粗糙度等；一根轴的圆柱度误差可能是由于刀具磨损、机床主轴回转误差、夹具变形误差等原因引起的.

6）工件的最终加工质量是由各误差源共同作用的结果.

2.3 机械加工误差建模

在机械加工过程中，工件一般需要经过粗加工、半精加工、精加工等阶段.工件的加工误差是机械加工工艺系统中各环节误差源的原始误差通过一定的误差传播途径，在工件上累积叠加耦合形成的［16］.

设工件在某道加工工序中存在m个加工误差，表示为Δδ＝（Δδ1，Δδ2，Δδ3，…，Δδm），且在该工序中存在n个加工误差源，表示为E＝（e1，e2，e3，…，en）.从几何误差的角度分析，每个误差源最多可能产生6个方向的原始误差，3个位置误差和3个角度误差.在笛卡尔坐标系下，设第j个误差源产生的原始误差表示为 Δξj＝（Δλj，x，Δλj，y，Δλj，z，Δθj，x，Δθj，y，Δθj，z）T.

设Δδi，j表示第j个误差源对第i个加工误差产生的误差分量，Ai，j为相应的误差传播系数，则有Am×n中各值可借助于齐次变换矩阵求出.

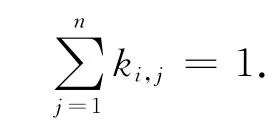
由以上分析可知：工件的加工误差主要取决于工艺系统中各误差源原始误差Δξj、各原始误差与工件加工误差间的传播系数Ai，j和误差源对各加工误差的影响程度即权重系数ki，j.因此，加工误差信息包含3个方面，即工艺系统各原始误差的大小、原始误差不同的传播途径［17-19］和加工误差源对各加工误差的权重系数.式（2）不仅表达了机械加工误差，亦表达了机械加工误差与误差源之间的关系.

3 知识库的建立

3.1 不确定性知识的表达

在知识库中，采用模糊量化的方式来表达不确定性知识.加工误差源诊断中的不确定性知识，采用“从定性到定量”的模糊量化方法将其数值化，即采用模糊数学的方法将定性知识合理地转化为定量知识.一个确定性概念可以用一个普通集合来表示，且一个普通集合可用一个特征函数来刻画.与此类似，一个模糊概念可用一个模糊子集来表示，且模糊子集也可用相应的隶属函数来刻画.因此，对于定性知识，只要合理确定它的隶属函数，就可以将其合理地量化.

3.2 知识库的结构

车削加工轴类零件的加工误差源诊断知识库，其知识组织形式按加工精度内容分为3大类：1）被加工零件产生形状误差的诊断知识（圆柱度、圆度等）；2）被加工零件产生位置误差的诊断知识（同轴度、垂直度、圆跳动等）；3）被加工零件产生尺寸误差的诊断知识.

每大类知识按照被加工零件材料（低、中、高碳钢和不锈钢）分为4个中类；每中类知识按照被加工零件的几何状态（刚性轴、细长轴、小轴）分为3个小类；每个小类对应的内容一是各可能误差源与工艺系统中零件加工误差间的关系确定度模糊向量，二是各可能误差源与工艺系统中零件加工误差间影响程度的权值模糊向量.车削加工误差源知识库结构，如图2所示.

图2 知识库组织结构Fig.2 Organization structure of knowledge base

4 加工误差源诊断

论域U＝｛主轴径向跳动，主轴运动精度，主轴分度精度，主轴回转精度，导轨平面度，导轨直线度，导轨磨损，工作台运动精度，工作台定位精度，工作台分度精度，工作台回转精度，刀具变形，刀具磨损，刀具调整装夹精度，工件材质，工件夹紧变形，工件热变形，工件加工余量，工件位置，测量误差，切削要素｝.模糊子集：A1为直线度；A2为平面度；A3为圆度；A4为圆柱度；A5为齿轮廓度；A6为面轮廓度；A7为平行度；A8为垂直度；A9为倾斜度；A10为同轴度；A11对称度；A12位置度；A13圆跳动；A14全跳动.

在进行误差源诊断时，通过人机交互方式将已加工好的工件误差特征信息用语言描述［20］，然后将所获得的零件加工误差信息转变成误差模糊向量，即

其中：a1，a2，a3，…，an元素代表零件在加工过程中加工误差表现出的程度.根据得到的误差模糊向量，由正向推理从已建立的知识库中得到各可能误差源与工艺系统中零件加工误差间的关系确定度模糊矩阵和影响程度的权值模糊矩阵

然后，利用模糊数学的原理方法，对误差源进行模糊逻辑运算和模糊诊断，由综合评判公式可得

模糊矩阵乘法采用欧几里得贴近度的方法计算，得到模糊向量（Bi和A）的贴近度为

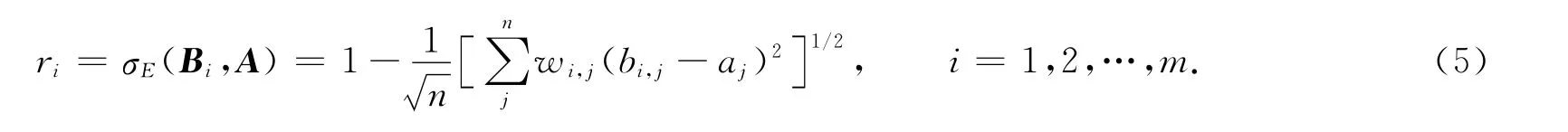
式（5）中：n为模糊向量A中的元素个数；m为工艺系统中误差源的个数.

然后反向推理，由计算出的模糊贴近度的大小及给定的阈值λ，依据阈值原则确定属于工件误差模糊子集A1～A14中的误差源.

5 实验验证与结论

实验采用精密车床CM6150，装夹方式为三爪卡盘及尾座顶尖，毛坯材料为直径为Φ40mm的45钢棒料，刀具为YT15（粗加工与半精加工）和YT30（精加工），切削液为5%的乳化液，测量仪器为圆柱度测量仪RS295C和游标卡尺.

车削加工基本工艺流程：毛坯（Φ40mm×205mm）—车削两端面与打中心孔—粗车各段外圆，三爪卡盘及尾座顶尖装夹—半精车，三爪卡盘及尾座顶尖装夹—精车，三爪卡盘及尾座顶尖装夹.加工一个刚性轴类零件，同批50件，如图3所示.其外圆由车床加工完成后，经测量知直径为Φ34mm轴段的圆柱度超差，测量结果如表1所示.

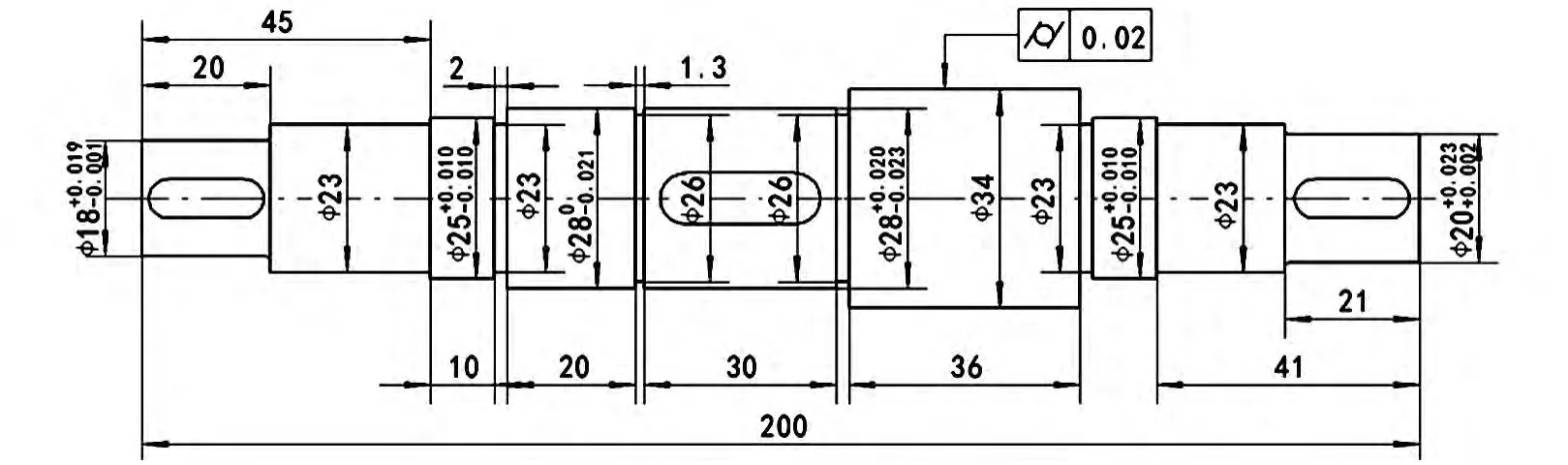
图3 零件简图（单位：mm）Fig.3 Parts diagram （unit：mm）

表1 圆柱度误差测量结果Tab.1 Measurement results of cylindricity error

经验与分析认为，产生该误差的主要原因是机床床身导轨误差、工件变形.因此，在诊断时，需要首先询问在整个加工过程中出现的一些情况和现象，如1）工件该轴段直径是否两端相差较大；2）加工过程中机床主轴转动平稳程度；3）工件加工过程中刀具表面是否有积屑瘤产生；4）工件表面是否凸凹不平；5）加工过程中工件是否多次装夹；6）加工后工件表面粗糙度是否超差；7）工件弯曲形变现象的程度 .通过对上述问题一一回答，得到回答是｛是；比较平稳；无；是；无；是；非常小｝.将以上信息转化成向量A＝［1，0.83，0，0.67，1，1，0］T.

对已建立的知识库进行搜寻，根据以上的模糊向量，可以得到对应的确定度向量和权重向量.

1）机床主轴回转误差 .B1＝（1，0，0，0，0.17，0，0），W1＝（0.23，0.23，0，0.11，0，0.43，0）；

2）床身导轨误差 .B2＝（0.67，0，0，0.83，0，0，0），W2＝（0.37，0，0，0.63，0，0，0）；

3）刀具刚度 .B3＝（0.83，0.5，0，0.67，0，0，0），W3＝（0.20，0.21，0，0，0，0.39，0.20）；

4）工件变形 .B4＝（0.67，0，0，0.33，0，0，0.5），W4＝（0.15，0，0，0.45，0，0，0.40）；

5）夹具装夹误差 .B5＝（0.33，0.17，0，0，0.5，0，0），W5＝（0.46，0，0，0，0.54，0，0）；

6）车削参数选择 .B6＝（0，0.5，1，0，0，1，0.83），W6＝（0，0.12，0.33，0，0，0.16，0.39）；

7）刀具几何角度 .B7＝（0，0.17，0.67，0，0，0，0），W7＝（0，0.28，0.31，0，0，0.41，0）.

由此得到关系确定度模糊矩阵和权重模糊矩阵分别为

由欧几里得贴近度公式计算模糊向量A与各可能误差源的贴近度，可得

最后根据阈值原则，由给定的截取阈值λ＝0.8和计算得出的贴进度可知r2＞λ，r4＞λ.运用反向推理得到引起工件圆柱度误差的工艺系统各可能误差源的权重矢量为

由所得权重矢量可知主要误差源有两点：1）机床导轨误差，其对工件误差影响的权重为0.297 6；2）工件变形误差，其对工件误差影响的权重为0.264 7.该结果与实际加工情况吻合.

［1］ 龚雯.机械加工误差源模糊智能诊断系统建模研究［J］.机械设计与制造，2003（5）：36-38.

［2］ 王帅强.基于进化计算的行为模型自动精化和排序学习方法的研究［D］.济南：山东大学，2009：3-13.

［3］ 任伟建，王重云，康朝海，等.基于神经网络和专家系统的故障诊断技术［J］.电器应用，2013，32（15）：66-71.

［4］ FU Xiao-jin.Novelty analysis and diagnosis system of error sources in machining based on expert system［J］.The Chinese Society of Mechanical of Engineers，2007，28（2）：225-232.

［5］ 卞玉涛，李志华.基于专家系统的故障诊断方法的研究与改进［J］.电子设计工程，2013，21（16）：83-87.

［6］ 朱芳.复杂零件加工过程质量控制理论与方法研究［D］.武汉：武汉理工大学，2011：3-21.

［7］ 龚雯.用于机械加工误差源诊断的模糊专家系统设计［J］.现代制造工程，2005（5）：97-100.

［8］ 吴常坤.基于SVM和模糊专家系统的机械加工工序质量诊断［J］.科技信息，2012（36）：433-434.

［9］ 谢季坚，刘承平.模糊数学方法及其应用［M］.武汉：华中科技大学出版社，2004：15-21.

［10］ CHEN De-gang，KWONG S，HE Qiang.Geometrical interpretation and applications of membership functions with fuzzy rough sets［J］.Fuzzy Sets and Systems，2012，193（16）：122-135.

［11］ 陈水利，李敬功，王向公.模糊集理论及其应用［M］.北京：科学出版社，2009：15-21.

［12］ ZENG Li，JIN Nong，ZHOU Shi-yu.Multiple fault signature integration and enhancing for variation source identification in manufacturing processes［J］.IIE Transactions，2008，40（10）：919-930.

［13］ 王秀艳.机械加工误差及提高加工精度分析［J］.中国新技术新产品，2012（4）：111.

［14］ 杜世昌，王猛，奚立峰.多工序加工系统产品尺寸误差传递建模［J］.机械工程学报，2011，47（16）：143-149.

［15］ 刘道玉，江平宇.基于误差传递网络的工序流波动分析［J］.机械工程学报，2010，46（2）：14-21.

［16］ JIAO Yi-bo，DJURDJANOVIC D.Compensability of errors in product quality in multistage manufacturing processes［J］.Journal of Manufacturing Systems，2011，30（4）：204-213.

［17］ 严子深.基于误差流理论（SOV）的机械加工误差诊断系统研究［D］.唐山：河北理工大学，2005：32-36.

［18］ 孙惠娟，殷国富，方辉，等.五轴数控机床综合误差建模评价方法研究［J］.四川大学学报：工程科学版，2012，44（6）：197-202.

［19］ LOOSE J P，ZHOU Shi-yu，CEGLAREK D.Variation source identification in manufacturing processes based on relational measurements of key product characteristics［J］.Manufacturing Science and Engineering-Transactions of the ASME，2008，130（3）：031007（1-11）（doi.org／10.1115／1.2844591）.

［20］ 龚雯.基于模糊理论的机械加工误差源智能诊断方法研究［J］.组合机床与自动化加工技术，2003（9）：33-35.