制动盘模态分析及其在生产线检测系统上的应用

褚志刚，叶方标，蒋忠翰，张昌福，周亚男

(1.重庆大学，机械传动国家重点实验室，重庆 400044;2.重庆大学机械工程学院，重庆 400044;3.重庆车辆检测研究院，国家客车质量监督检验中心，重庆 401122)

前言

当制动盘在持续制动时其表面温度高，摩擦副摩擦因数降低，产生热衰退，进而降低汽车的制动性能并影响制动安全性，其中散热辐条等结构对制动盘散热性能的影响尤为明显［1］。散热辐条等结构尺寸和铸造缺陷不易在生产线上快速和直接检测，且对制动盘的固有频率有显著影响［2］。Ford、TRW等国外知名汽车及其零部件企业均采用在线测量固有频率的方法来检测制动盘的生产质量，并依据测量得到的低阶固有频率数值是否处于允许容差范围内来判断其合格与否［3］。合理的固有频率容差非常重要，容差的确定可采用类比评价法和分析评价法，其中类比评价法是以多个加工质量良好的制动盘样本为对象进行测量获取其固有频率的统计值，此法简便易行，但无法对影响制动盘固有频率的容差因素进行定量分析;而分析评价法则可依据制动盘自身的结构，通过有限元概率设计［4］等方法确定其在生产许可的误差范围内的容差。

本文中以试验模态分析［5－12］修正后的制动盘有限元模型为基础，针对制动盘各尺寸允许公差范围，采用有限元概率设计方法，确定了前5阶固有频率的容差。

1 试验模态分析

由于制动盘结构尺寸和阻尼都较小，振动能量在结构中的传递消耗较少，且实际制动盘固有频率在线检测时常采用锤击法［3］，故本文中在进行模态试验时也采用锤击法。试验系统简易框图如图1所示，图2左图为试验现场照片。试验时首先通过B＆K 3560型数据采集系统同时采集制动盘的力锤激励力信号和粘贴在制动盘上传感器的振动加速度响应信号，并利用PULSE软件进行信号处理，得到各响应点和激励点之间的频率响应函数。之后，再利用PULSE Reflex Mode模态分析后处理软件提取制动盘的前9阶模态参数。为获得与制动盘设计尺寸最为接近的模态结果，试验时采用精密加工获得的标准制动盘，该制动盘除倒角、散热辐条长度等不易直接精确测量外的主要尺寸均经过准确测量。

鉴于制动盘的旋转对称性，将制动盘沿周向均匀划分为10等份，得到如图2右图所示的制动盘测量网格结构模型。试验时将制动盘放置在泡沫塑料上，确保制动盘第1阶弹性体模态频率高于整体刚体模态频率10倍以上，进而保证制动盘近似处于无约束的自由状态，所得模态结果则可认为是该制动盘本身的弹性模态。由于制动盘结构存在旋转对称性，导致制动盘必然存在大量的模态频率基本一致、振型正交的强耦合重根模态。因此，本文中采用移动力锤激励、固定3个加速度响应测点的方法进行频率响应函数测量，加速度传感器分别布置在盘体27号、30号和凸台50号节点上，通过测量系统频率响应函数矩阵的3行来准确分离出耦合度较高的重根模态。

图3为节点27和30的传递函数的互异性检验，可见两曲线近似重合，既表明制动盘质量矩阵、刚度矩阵、阻尼矩阵和频率响应函数矩阵近似为对称矩阵，又表明试验测量得到的频率响应函数质量良好。

对于大量的重根强耦合模态，本文中采用能有效识别重根模态的最小二乘复频域方法［4，13］结合稳态图［12－13］和复模态指示函数识别重根强耦合模态，其中稳态图如图4所示，3条曲线分别对应于3个复模态指示函数。

从图4可见，在1 060、2 360、2 460和2 800Hz左右均有2条复模态指示函数曲线出现较大峰值，且在稳态图上均出现了2个非常接近且极其稳定的模态频率(特征值)，表明在上述频率附近均存在2阶模态，而对应1 980Hz左右只有1条复模态指示函数出现较大峰值，表明在该频率附近只存在1阶模态。最终得到的制动盘前9阶固有频率和模态阻尼如表1所示。

表1 试验模态参数识别结果

前9阶试验模态振型如图5所示。由于制动盘是关于中心轴对称的旋转对称结构，因此分析中通常利用节圆和节径来表示制动盘的模态振型特征。(n，m)模态表示模态振型存在n个节圆和m个节径。模态(0，m)代表各阶周向模态，模态(n，0)代表各阶轴向模态;当m和n均不为零则代表组合模态［2］。第1、2阶振型均为具有2条正交节径的周向模态，即为(0，2)周向模态，这两阶模态之间的对应节径相差π/4;第3阶振型为具有1个节圆的第1阶轴向伸缩变形，对应于(1，0)轴向模态;第4、5阶振型则具有3条均匀分布节径的周向模态，各节径之间夹角为π/3，对应于(0，3)周向模态，且这两阶模态之间的对应节径相差π/6;第6、7阶振型则是具有1个节圆、1条节径的组合模态，即为(1，1)组合模态，且这两阶模态节圆位置相同，节径相互正交;第8、9阶振型是具有1个节圆、2条相互正交节径的组合模态，即为(1，2)组合模态。

2 有限元模态分析

该制动盘采用砂箱分型模铸造工艺，结构存在较多倒角和沟槽等，在不影响模态结果准确性的原则下对上述细节进行简化处理，减少了实体建模的时间和整个模型的复杂度，提高了单元质量。制动盘材质为HT250，弹性模量为1.17×1011Pa，密度为7 000kg/m3，泊松比为 0.27。

由于该制动盘具有旋转对称性，为提高有限元模态分析、特别是后续有限元概率设计的计算效率，本文中只建立其1/5的子结构模型，如图6(a)所示。为能反映内部的散热筋板结构和分布，对该图做适当的剖视处理，如图6(b)所示。选用Solid 92单元对制动盘划分网格后，得到如图6(c)所示的有限元网格模型。在此基础上，选用Block Lanzos方法基于有限元模型采用旋转对称算法提取该制动盘的前9阶自由状态下的弹性模态频率和振型。

表2列出了该制动盘有限元模态分析和试验模态分析获得的各阶固有频率的相对误差，图7为各阶模态对应振型。从表2、图5和图7可见，试验模态和有限元模态的固有频率和振型均吻合良好。

表2 试验模态频率与有限元模态频率的对比

3 固有频率容差范围确定

考虑工程实际的不确定因素，有限元分析的任何一个输入数值在某种程度上都具有不确定性。对于同批生产的零件来说，几何尺寸、加工误差和材料等都不可能完全一样［14］。为研究不确定因素对产品性能和质量的影响，采用有限元分析技术与概率设计技术相结合的有限元概率设计技术。

制动盘参数模型如图8所示。根据企业目前加工设备和工艺水平所能达到的技术指标和制动盘散热特性对结构关键尺寸的需求，且结合国标GB9439—2010，规定的各尺寸偏差如表3所示。对若干制动盘多个易测量几何尺寸参数测量结果表明，该制动盘的上述实际尺寸可以认为近似服从均匀分布。采用参数化命令建模，以上述有限元模型选择旋转对称计算方法在ANSYS的PDS模块中计算，采用Monte Carlo法进行3 000次随机抽样仿真。得到具有99.7%的置信度的前9阶固有频率范围，如表4所示。

表3 制动盘参数 mm

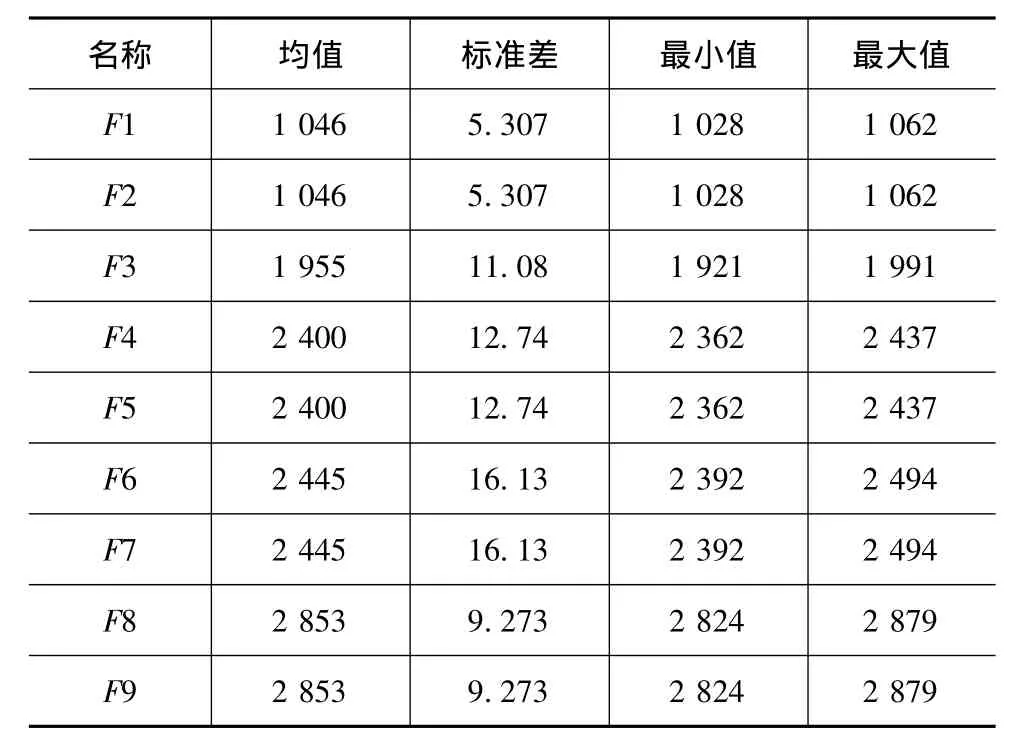
表4 置信度为99.7%的前9阶固有频率范围 Hz

需要指出的是，在文献［3］中，制动盘固有频率在线检测系统采用峰值法识别其各阶固有频率，此方法本质上是单自由度方法，无法对制动盘的重根模态进行解耦识别。因此，在线检测系统检测到的第1阶固有频率对应为该制动盘的第1、2阶模态频率，第2阶固有频率对应为该制动盘的第3阶模态频率，第3阶固有频率对应为该制动盘的第4、5阶固有频率，第4阶固有频率对应为该制动盘的第6、7阶，第5阶固有频率对应为该制动盘的第8、9阶，从而仿真须计算制动盘的前9阶固有频率分布范围。

图9为上述制动盘第1阶固有频率对于各参数的灵敏度，图中对于影响不显著(灵敏度＜2.5%)的变量未予显示，为节约篇幅，其他各阶固有频率对各参数的灵敏度以图10的形式给出。由图可见，影响最大的结构参数依次为 Y7、R、Z4、Y5、Z3、Z5、Z6，即盘体直径、散热辐条宽度、盘体内圈厚度、盘体外圈长度、沟槽深度、散热辐条高度和盘体外圈厚度等尺寸，显然通过观察固有频率的变化能有效解决制动盘在生产线上加工质量不易快速在线检测的问题。

综上所述，最终确定的该系列制动盘前5阶固有频率的在线检测容差范围如表5所示。

表5 在线检测系统前5阶固有频率容差范围

4 结论

首先对制动盘进行了试验模态分析和有限元模态分析，对比二者的分析结果，在此基础上，利用有限元概率设计方法对影响制动盘固有频率的各结构设计变量进行灵敏度分析，计算制动盘固有频率的变化范围，得出如下结论。

(1)制动盘有限元模态与试验模态分析结果吻合良好，前9阶固有频率的最大相对误差小于2%，振型亦吻合良好，表明该有限元模型准确。

(2)由制动盘固有频率对各结构设计变量的灵敏度分析结果表明，制动盘盘体直径、散热辐条宽度、盘体内圈厚度、盘体外圈长度、沟槽深度、散热辐条高度和盘体外圈厚度等尺寸显著影响制动盘的各低阶固有频率，通过观察固有频率的变化能有效解决上述结构参数在生产线上不易快速检测的问题，能实现制动盘质量的快速在线检测。

(3)利用有限元概率设计技术确定制动盘前5阶在线检测固有频率的容差范围。有限元概率设计技术为在线检测系统各阶固有频率容差设定提供了有效分析手段。

［1］ 赵凯辉．汽车制动器热衰退性能及相关制动安全检测研究［D］．西安:长安大学，2010．

［2］ 张立军，权循宇．制动盘几何特征对结构模态特性影响仿真分析［J］．系统仿真学报，2009，21(19):6256 －6259．

［3］ 褚志刚，周亚男，蒋忠翰，等．制动盘固有频率在线检测系统的设计［J］．机械科学与技术，2012，31(5):723 －725．

［4］ 周云，易伟健．用PolyMAX方法进行弹性地基板的实验模态分析［J］．振动与冲击，2007，26(7):139 －143．

［5］ 李小华，沈贝，蔡忆昔，等．4105型柴油机曲轴计算模态与试验模态的振型相关性［J］．农业工程学报，2011，27(11):51 －55．

［6］ 曹奇英，张准，李健康，等．基于内积的模态相关分析［J］．应用力学学报，1998，15(4):135 －138．

［7］ 朱茂桃，何志刚，徐凌，等．车身模态分析与振型相关性研究［J］．农业机械学报，2004，35(3):13 －15．

［8］ 周长路，范子杰，陈宗渝，等．微型客车白车身模态分析［J］．汽车工程，2004，26(1):78 －80．

［9］ 郭荣，周鋐．某型轿车白车身试验模态分析及动态特性评价［J］．机械设计，2010，27(8):18 －22．

［10］ 左言言，方玉莹．拖拉机发动机罩振动的模态相关分析［J］．农业机械学报，2003，34(3):15 －18．

［11］ 杨建国，胡旭刚，李玉军．4120SG柴油机机体动态特性分析［J］．振动与噪声控制，2008，24(4):24 －26．

［12］ 杨毅青，刘强，Munoa Jokin．基于正交多项式和稳定图的密集模态参数辨识［J］．振动、测试与诊断，2010，30(4):429 －433．

［13］ Bart Peeters，Herman Van der Auweraera，Patrick Guillaumeb，et al．The PolyMAX Frequency-domain Method:a New Standard for Modal Parameter Estimation［J］．Shock and Vibration，2004，31(1):395－409．

［14］ Pandey A K，Biswas M，Samman M M．Damage Detection from Changes in Curvature Mode Shapes［J］．Sound and Vibration，1991，145(2):321 －332．