基于绿灯时间等饱和度的TD学习配时优化模型*

邵 维，张吉光，刘改红

（1.贵阳职业技术学院轨道交通分院，贵州贵阳 550000；2.玉屏县公路管理所，贵州铜仁 554000）

基于绿灯时间等饱和度的TD学习配时优化模型*

邵 维1，张吉光2，刘改红1

（1.贵阳职业技术学院轨道交通分院，贵州贵阳 550000；2.玉屏县公路管理所，贵州铜仁 554000）

首先对传统的绿灯时间等饱和度概念进行了扩展，提出了分级绿灯时间等饱和度.在此基础上，针对分级绿灯时间等饱和度目标，构造了奖赏函数，采用了模糊方法解决流量状态空间维数爆炸问题，建立了定周期和变周期两种模式下的四种离线TD学习配时优化模型.通过Matlab编程，开发了这四种模型的计算程序，相对于在线TD学习模型，离线TD学习模型更适合交叉口信号配时优化.以一个两相位控制的单交叉口配时优化作为算例，对比分析了四种模型的性能.总体上变周期模式的离线TD学习模型可以获得解的结构、最优解的分布，这是传统配时理论不具备的.定周期条件下，奖赏分级的效果不明显；变周期条件下，奖赏分级效果明显，交通性能更优.

配时优化；绿灯时间等饱和度；TD方法；状态模糊；变周期

目前，交通问题已成为影响社会经济发展、人民生活水平提高的一个制约因素，交通问题已越来越受到人们的重视.然而交叉口信号灯控制的方法是交通控制要解决的核心问题.平面交叉口的通行能力不足是造成大城市交通拥堵的主要原因之一，因此，如何优化交通信号控制系统是交通管理中关键的工作.现代交通信号控制的类型五花八门，但单个交叉口的交通信号控制是交通控制网中最基本的节点，它的信号控制优化是解决城市交通拥堵的基础.继定时控制和感应控制这两种控制方法之后，自适应控制系统［1］在交通信号控制中的应用取得了更为满意的结果.本文立足于研究单个交叉口的信号灯控制问题，采用强化学习［2］中的TD（Temporal Difference）学习算法［3］，对单交叉口信号灯控制方法进行研究，试图研究和开发解决交叉口信号灯控制的新方法和新思路.

1 TD学习原理简介

强化学习是一种不同于监督学习的一种学习方法，将学习视为一种试错交互的过程［4］.其原理是：学习系统通过感知环境的变化，根据自身目前所处的状态，采取一个行为作用于环境，环境由于受到其行为的影响而产生变化，同时给予学习系统一个强烈的信号（奖励或惩罚），学习系统再根据当前环境的变化以及反馈回来的信号，调整自身的行为，调整的原则是寻找自己获得最大奖赏值的行为.选取的行为不仅影响当前的行为还会影响到下一时刻的状态及最终的学习效果.

瞬时差分（TD）算法是强化学习算法中的中心算法，它结合了动态规划和蒙特卡罗方法，是一种增量式的学习算法，很大程度上能表示强化学习的核心思想和新意.瞬时差分算法能直接从交互经验中学习，在学习过程中逐步进行修改，而不需要基于环境的动态信息模型，也不需要在最终输出结果产生之后再修改以往学到的经验.TD、动态规划和蒙特卡罗三者之间的关系是强化学习理论反复出现的理论［5］. Q－学习控制算法是强化学习发展中最重要的一个突破，它是的一个离线的TD控制方法.

2 基于绿灯时间等饱和度的状态模糊TD学习模型

SCATS系统提出了绿灯时间饱和度的概念，即被车流有效利用的绿灯时间与绿灯显示时间之比.SACTS系统绿信比优化的大致过程［6］如下：在每一信号周期内，都要对四种绿信比方案进行对比，对它们的“入选”进行“投票”.若在连续的三个周期内某一方案两次“中选”，则该方案即被选择作为下一周期的执行方案.绿信比方案的选择与信号周期的调整交错进行，两者结合起来，是对各相位的绿灯时间不断调整的结果，使各相位饱和度维持大致相等的水平，即“绿灯时间等饱和度”原则.SCATS控制系统的应用效果证明了绿灯时间等饱和度原则的有效性，但是该系统利用“投票”对绿信比进行小步距优化的方式是在四个解空间中进行优化，虽然保证了配时方案的连续性、小波动，但是难以保证解的最优化.本文突破了传统的绿信比优化受周期固定限制的不足，分别对定周期、变周期两种模式下的配时模型进行了研究.

2.1 建模方法

2.1.1 算法的模式选择

对于交通信号配时优化问题，若采用在线学习模式，学习算法会对未知的交通状态进行探索，将会产生一些性能不好的配时方案，那么可能会导致交叉口交通的拥堵，甚至交通中断.因此，将在线学习算法用于交通信号控制问题不理想.离线学习模式更加适合交通信号控制，具体地，先建立交通控制问题的模型，再利用离线学习算法对各种交通状态及配时方案进行学习，从而得到不同交通状态下的最优配时方案，最后将最优配时方案应用到实际交叉口的交通信号控制中.为加快离线学习模式的学习速度，在每个时间步随机等概率选择状态和行为［7］.

2.1.2 模型建立的关键因素

状态、行为、奖赏是强化学习方法的三个要素，建模的重点是如何处理这三个要素.模型通过迭代计算达到收敛.

TD控制中Q学习算法步骤为：

（1）设定学习速率、折扣因子和奖励函数；

（2）初始化Q矩阵；

（3）利用策略选择行为后，作用于环境，状态转移到下一个状态，并获得当前奖赏值；

（4）Q值更新函数为

（5）设置下一状态为当前状态；

（6）重复（3）－（5）步直至达到目标状态.

因此，利用TD控制的Q学习算法对单交叉口的信号进行调节，需要确定以下参数：

①选取学习的状态集；

②选取学习的行为集；

③确定状态转换之后的奖励函数r（s，a）；

④确定学习系统的行为选择策略.

⑤设定算法的学习速率α和折扣因子γ．

本文中状态选取交通流量，行为选取相位绿灯时间，奖赏建模为绿灯时间等饱和度.交叉口的饱和度管理是交通管理的重要组成部分，通过饱和度管理可以将交通压力在路网中合理分担，如将交通压力较大的上游路口饱和度适当提高，可以减轻本交叉口的交通压力.本文将传统的Scats系统中的绿灯时间饱和度概念进行了扩展，提出分级的绿灯时间饱和度概念，即将0至1之间的饱和度值进行分级，处于不同的饱和度时给予的奖励不同.设定学习速率α＝0.1，折扣因子6002＝0.8，初始化Q矩阵为零矩阵.

2.1.3 状态模糊函数的选取

为便于对模型结果进行分析，说明模型的正确性和有效性，以两相位控制的单交叉口为例进行研究.交叉口进口道的饱和流量为1600pcu／h，本章中到达流量的区间设为0至600puc／h，在两相位的情况下共有6002个状态，属于维数灾难问题，难以对整个状态集进行学习.首先采用离散化思想对状态和行为进行了离散，将每个相位的流量进行离散分为4个状态，离散间隔分别为［0，150］、［150，300］、［300，450］、［450，600］，用1，2，3，4来表示流量所处的区间.流量区间为150，由于交通流的随机性离散区间过大会影响的准确性，为了解决这一问题本章将到达的流量进行模糊.

交通流的论域为［0，600］（单位：辆／h），模糊的集合语言值为“很小（Verysmall，VS）”、“小（Small，S）”、“中等（Medium，M）”、“大（Big，B）”.隶属度函数［8］为三角形分布.由此可以得到交通流的隶属度函数曲线如图1所示.

图1 隶属度函数曲线

我们用1，2，3，4来表示流量所处的集合，对于两相位的交叉口每个相位的流量状态选择关键进口道的流量，用（i，j）表示两个相位的关键流量所处的状态区间，由此可得该算法中任然有16个流量对，即16个状态，分别为（1，1）、（1，2）、（1，3）、（1，4）、（2，1）、（2，2）、（2，3）、（2，4）、（3，1）、（3，2）、（3，3）、（3，4）、（4，1）、（4，2）、（4，3）、（4，4）.因此，对于同一个流量对它们所处的状态可能是不同的，例如对于流量对（100，100）所处的状态就有可能是（1，1）、（1，2）、（2，1）、（2，2）这四种状态，它们的概率由隶属度函数划分，且概率之和等于1.

选取绿灯时间对为行为，相位的最短绿灯时间为10s，最长绿灯时间为50s；且取2s的时间间隔，则可知每个相位的行为有21个，可以选择表示为g＝｛10，12，14…48，50｝，相应地对行为进行编号A∈｛1，2，3…20，21｝.采用60s的固定周期时共有21个行为，采用［30s，110s］的变周期共有441个行为.为了减小随机性带来的Q值波动，本文采用200个程序同时运行，相当于200个相同交叉口同时运行，然后对这200个同时运行的程序的Q值取平均值来判定是否已经收敛.

2.2 定周期奖赏不分级的状态模糊TD学习优化模型

周期固定为60s，相位的关键进口道流量为0～600pcu／h，状态和行为建模如2.1.3所述.提出了如下的奖励函数：

式中r为奖励值，DSX、DSY分别表示两个相位的绿灯饱和度.

优化结果如图2所示，横坐标表示的是行为，纵坐标表示的是状态，每个小方格内的颜色表示Q值，对于每个状态（即每一行）颜色最深的行为是该状态的最优行为.对于状态（1，1）、（2，2）、（3，3）、（4，4）四个状态的两相位的关键进口道流量处于相同的流量区间，如图所示取得的最优行为是11号行为，即信号配时方案为（30s，30s），说明该模型是正确的.对于这个模型，16个状态下最优解是唯一的.

图2 定周期奖赏不分级的状态模糊TD学习优化模型

2.3 定周期奖赏分级的状态模糊TD学习优化模型

周期固定为60s，相位的关键进口道流量为0～600pcu／h.状态和行为建模如前所述.提出了如公式（3）所示的奖励函数，其物理意义是控制交叉口在近饱和状态下运行.本例中对饱和度处于0.85至0.95之间给予最大奖励，随着饱和度减小，奖励值减小，过饱和时奖励为0，即为惩罚.这个公式可以根据管理者期望的饱和度值进行修改.

式（3）中r为奖励值，DSX、DSY分别表示两个相位的绿灯饱和度；f（ds）如（4）所示，式（4）中ds表示两相位饱和度的均值，即ds＝（DSY＋DSY）／2．

优化结果如图3所示，与2.2部分的优化结果类似，这是由于受到周期固定的约束，导致奖赏分级和奖赏不分级的结果类似.

2.4 变周期奖赏不分级的状态模糊TD学习优化模型

本部分研究周期可变、奖赏不分级的情况下解的结构.周期变化范围是30至110秒，相位的关键进口道流量为0～1200pcu／h.本文提出的奖励函数如下：

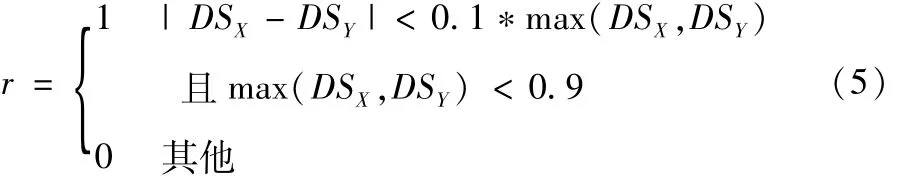
式（5）中r为奖励值，DSX、DSY分别表示两个相位的绿灯时间饱和度.

优化结果如图4所示，给出了16种状态下的最优解，最优解是不唯一的.图中的每个小图表示一个状态的优化结果，小图的横纵坐标表示的是两个相位采取的行为即绿灯时间，Q值大小用颜色表示，颜色越深的位置表示该行为越优.从该图可知，在变周期条件下最优解是不唯一的，呈带状.

图3 定周期奖赏分级的状态模糊TD学习优化模型

2.5 变周期奖赏分级的状态模糊TD学习优化模型

本部分研究周期可变、奖赏分级的情况下解的结构.周期变化范围是30至110秒，相位的关键进口道流量为0～600pcu／h.当流量一定时，饱和度随着周期的增大而减小.但是当周期较小时导致饱和度的变化量较大；随着周期不断增大，饱和度的变化量减小，趋近于一条直线，导致在较大周期的时候无法分别行为的性能优劣.因此，构造的奖励函数是当交叉口饱和度小于0.9时，随着周期的增大，奖励逐渐减小.提出的奖励函数如下：

式（6）中：r为奖励值；DSX、DSY分别表示两个相位的绿灯时间饱和度；C表示周期.

优化结果如图5所示，给出了16种状态下的最优解，最优解是不唯一的，呈带状.图中的每个小图表示一个状态的优化结果，小图的横纵坐标表示的是两个相位采取的行为即绿灯时间，Q值大小用颜色表示，颜色越深的位置表示该行为越优.状态（1，1）、（2，2）、（3，3）、（4，4）的最优解处于对角线上.对于每一列，即第二相位的流量区间相同时，随着第一相位流量的增大，行为的选择向右下方偏移，即选择第一相位的绿灯时间增加，第二相位的绿灯时间减少的行为集.对于每一行，即第一相位的流量区间相同时，随着第二相位流量的增大，行为的选择向左上方偏移，即选择第二相位的绿灯时间增大，第一相位的绿灯时间减小的行为集.

与变周期奖赏不分级的优化结果图4比较，最优解更加集中，对奖励进行分级有利于选择等饱和度值更大的行为对.

图4 变周期奖赏不分级的状态模糊TD学习优化模型

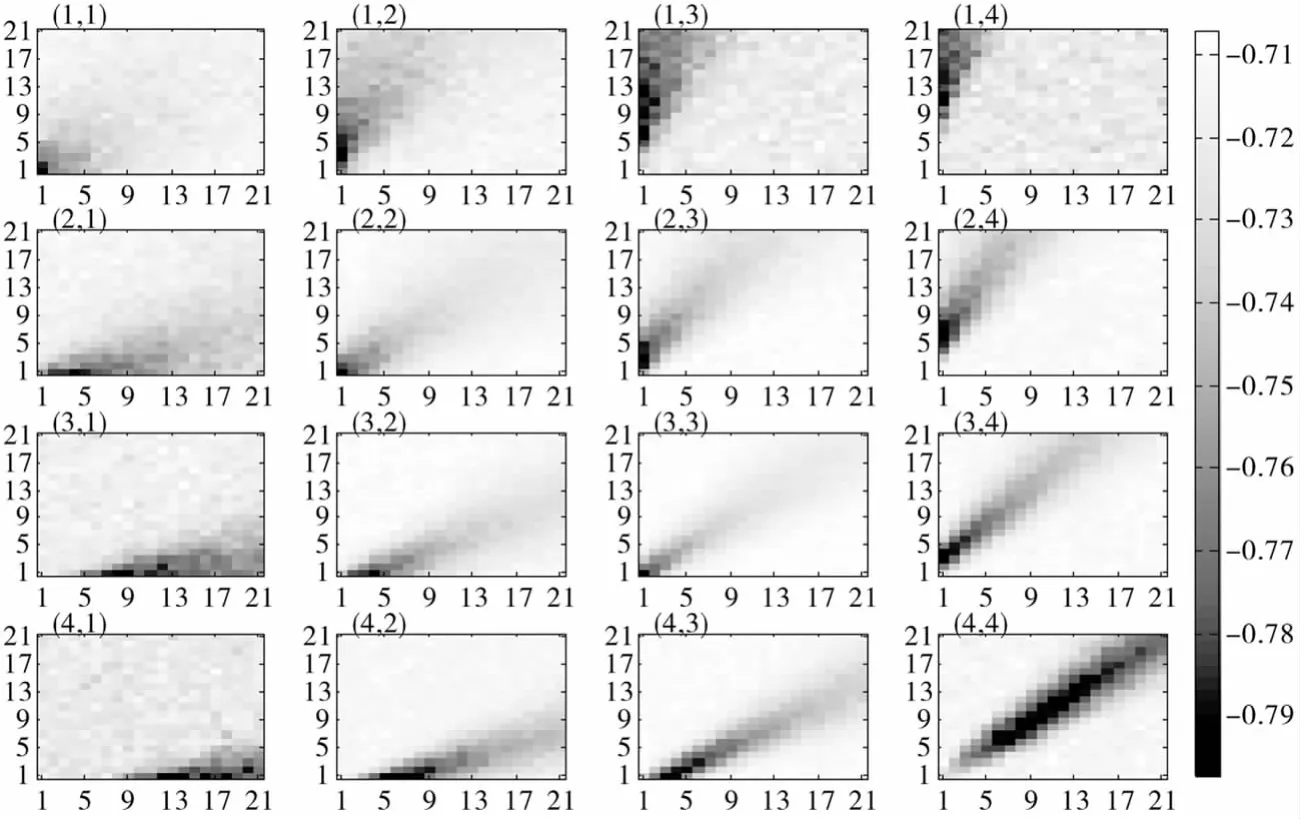
图5 变周期奖赏分级的状态模糊TD学习优化模型

模型对状态集进行了模糊，它的优点在于同一个流量它可能处于不同的状态，这样将状态集的边缘模糊化有利于选取更优的行为.例如：流量取（260，470），它可能的状态为（2，3）、（2，4）、（3，3，）和（3，4）这四种状态.提高了交通量处于同一状态区间最优配时方案的选择.

3 结论

（1）本文建立了单交叉口配时优化的离线TD学习模型.相对于在线TD学习模型，离线TD学习模型能够历遍整个解空间，弄清楚解的结构，事先知道性能较优的解的分布、性能较差的解的分布、最优解，这是传统配时理论不具备的.

（2）针对绿灯时间等饱和度的优化目标，本文建立了定周期和变周期两种模式下的离线TD学习模型，算例结果表明定周期模式下最优解是唯一的，变周期模式下最优解是不唯一的，呈带状.对于最优解不唯一的解结构，可以将这些解作为一个最优解的方案库，当检测器检测到交通流量时，从方案库中进行选择.这时可以考虑与上一个配时方案周期接近、与相邻交叉口周期接近等因素，提高配时方案与其他因素的兼容性、鲁棒性，这是传统配时理论不具备的.

（3）相比传统的Scats系统的小步距调整方式，离线TD学习模型能够实现流量变化小的时候，方案变化不大；流量变化大时，又能很快地调整方案，具有更强的适应性.

（4）对状态离散区间的模糊，增加了状态寻优的区间，有利于不同的交通量选取更优的配时方案.

［1］Stevanovic A.Adaptive Traffic Control Systems：Domestic and Foreign State of Practice［M］.Washington D C：Transportation Research Board，2010.

［2］Sutton R S，Barto A G.Reinforcement Learning－An Introduction［M］.Cambridge：The MIT Press，1998.

［3］Kaelbling L P，Littman M L，Moore AW.Reinforcement learning：a survey［J］.Journal of Artificial Intelligence Research，1996，（2）：237－285.

［4］马寿峰，李英，刘豹.一种基于Agent的单路口交通信号学习控制方法［J］.系统工程学报，2002，（6）：526－530.

［5］刘越伟，张海波.基于SCOOT交通控制系统的信号灯倒计时研究及应用［J］.交通标准化，2012，（1）：145－147.

［6］全永燊.城市交通控制［M］.北京：人民交通出版社，1989.

［7］卢守峰，邵维，韦钦平.基于绿灯时间等饱和度的离线Q学习配时优化模型［J］.系统工程，2012，（5）：117－122.

［8］谢季坚，刘承平.模糊数学方法及其应用［M］.武汉：华中科技大学出版社，2006.

（责任编校：晴川）

The Optim ization M odel of TD Learning Tim ing Based on the Green Time Equi－saturation

SHAOWei1，ZHANG Jiguang2，LIU Gaihong1
（1.Track Transportation Branch of Guiyang Vocational and Technical College，Guiyang Guizhou 550000，China；2.Highway Management Office of Yuping，Tongren Guizhou 554000，China）

We propose themulti－level green time saturation.On this basis，for the classification of green time saturation target，the study constructs a reward function，uses the fuzzymethod to solve the traffic state space dimension explosion problem，and establishes four optimization models of offline TD learning under fixed period and variable cycle twomodes.Using a two－phase control of a single intersection as an example，the study comparatively analyzes the performance of fourmodels.Generally speaking，offline TD learning model of variable cyclemode can obtain the structure of solutions and the optimal solutions distribution，which does not belong to the traditional timing theory.Under the fixed period condition，reward grading effect is not obvious，while under the variable cycle condition，reward grading effect is obvious and the traffic has better performance.

timing optimization；green time equi－saturation；TD control；state fuzzy；variable cycle

U491

A

1008－4681（2014）05－0070－05

2014－06－09

邵维（1988－），女，湖南岳阳人，贵阳职业技术学院轨道交通分院教师，硕士.研究方向：轨道交通运营管理、交通运输规划与管理.