集中荷载作用下工字型钢－混凝土组合梁稳定性研究*

卜伟斐

（江西工业工程职业技术学院采矿与建筑工程系，江西萍乡 337000）

集中荷载作用下工字型钢－混凝土组合梁稳定性研究*

卜伟斐

（江西工业工程职业技术学院采矿与建筑工程系，江西萍乡 337000）

钢—混凝土组合梁结构是当前土木工程建设中重要的建筑结构形式，其承载能力的有效发挥对于实际工程意义重大.但是，当前对于钢—混凝土组合梁结构稳定性计算方法以及结构设计还没有较为明确的标准和规范，所以给工程实际带来很大的不便.对集中荷载作用下工字型钢—混凝土组合梁结构的侧向失稳问题进行研究.根据集中荷载作用下工字型钢—混凝土组合梁变形特征，建立了集中荷载作用下组合梁翼缘侧向屈曲失稳的力学模型以及侧向弯扭力学模型.运用能量法，分别求解两种模型的结构变形势能，并根据势能驻值原理，采用变分法，进行结构失稳临界荷载的求解.并通过对两种模型的对比，来确定更加便于工程实践的力学模型和计算方法；通过实例对文中两种模型下的临界失稳求解计算方法进行验证，并与国内外关于组合梁稳定性的计算模型和方法进行比较，验证计算模型和计算方法的可行性.

钢－混凝土组合梁；集中荷载；侧向屈曲失稳；临界荷载

近年来，钢－混凝土组合结构广泛地应用于超高层建筑、大跨桥梁等工程领域.钢－混凝土组合结构把钢结构和混凝土结构的优点相结合，具有良好的社会效益和技术经济效益，已成为应用前景广阔的新型结构体系.而作为组合结构中重要的横向承重构件——钢－混凝土组合梁，其研究结果对组合结构在实践中应用推广起着举足轻重的作用.

R.Narayanan［1］等研究了在动荷载作用下，钢梁腹板可能发生的局部屈曲，指出钢梁腹板的局部屈曲将引发翼缘的较大变形，同时建议了避免局部屈曲设计方法；Fukumoto和kubo［2］采用线弹性有限元方法计算了受压下翼缘整体侧向失稳弯矩；Weston［3］在对连续组合梁有限元分析基础上，考虑了钢梁初始变形和局部失稳的影响，实现组合梁塑性铰内力重分布；南非学者N.W.Dekker［4］等人把梁分为正弯矩区和负弯矩区，讨论了正弯矩区和负弯矩区不同的计算方法，给出了考虑腹板局部屈曲的分析模型；英国桥梁规范［5］将组合梁的侧向失稳转化为弹性地基上压杆稳定问题，通过求等效压杆长度来计算临界应力值.

但对钢－混凝土组合梁稳定性方面的试验和理论研究工作还是比较少.就整体稳定性而言，组合梁远优于纯钢梁，但现在对组合梁整体稳定性的研究计算依然沿用钢结构设计规范中钢梁侧向失稳设计方法.在钢－混凝土连续组合梁实际工作过程中，当其承受较大的可变荷载及不利荷载分布时，受压的钢梁下翼缘可能发生侧向失稳.单纯的按钢结构设计规范计算组合梁的稳定问题，大大限制了组合梁的结构及经济性能的有效发挥，因此，对在集中荷载作用下钢－混凝土组合梁的整体稳定性问题进行研究是非常必要.本文主要研究在集中荷载作用下工字型截面钢－混凝土组合梁稳定性.

1 工字型钢－混凝土组合梁梁翼缘失稳计算方法

1.1 工字型钢－混凝土组合梁梁翼缘侧向屈曲失稳

理论分析采用如下基本假定：材料是各向同性的完全弹性体；构件为等截面梁且无缺陷；构件的侧向弯曲变形是微小的；平面内在屈曲前的弯曲变形对侧向屈曲的影响不考虑；工字钢翼缘的形状保持不变不考虑初始缺陷、残余应力和梁的扭转变形；钢梁上翼缘由于受到混凝土翼板的约束不能发生侧向变形和扭转变形；忽略混凝土的抗弯作用，只考虑混凝土翼板中钢筋的抗弯作用.

1.1.1 屈曲失稳模型

工字型钢－混凝土组合梁的弹性临界荷载Fcr，力学模型如图1所示.

图1 屈曲失稳力学模型

1.1.2 屈曲失稳应力分布

根据钢－混凝土组合梁结构受力情况，基于弹性力学，将整体结构简化为平面应力问题.平面内某一单元的应力分

根据弹性力学相关内容，求解得到钢梁腹板的变形uW见下式（1）布如图2所示，模型中以压应力为正.

图2 平面单元应力分量示意图

组合梁在横向集中荷载作用下，工字钢截面的纵向应力（z方向应力）可表示为，

其中σtz为组合梁结构上翼缘纵向应力；σwz为组合梁结构工字钢腹板纵向应力；σbz为工字钢下翼缘的纵向应力；h0为工字钢上翼缘与下翼缘重心轴之间的距离；I为全部钢材截面绕其中性轴的惯性矩；M（z）为组合梁各横截面的弯矩，以组合梁上翼缘受拉为正；yc为组合梁纵向弯曲中性轴到x轴的距离.

横向荷载作用下，组合梁结构工字钢横截面的剪应力计算表达式为：

对于集中荷载作用下的组合梁，根据材料力学［6］中工字型截面梁的横截面剪应力的分布分析可知，腹板承担了横截面上绝大部分的剪力，翼缘承担了横截面的绝大部分弯矩.因此，在计算中只考虑腹板上的剪应力τwzy的作用，而忽略翼缘剪应力τtzy和τbzy的作用.

1.1.3 屈曲失稳势能

在弹性力学中薄壁构件变形问题是一个较为复杂的问题，特别是当结构荷载和边界条件复杂的情况下，很难建立像普通平面应变问题的微分方程，更无法通过一般的弹性力学方法进行求解，得到准确的理论变形.所以，在薄壁构件变形问题求解过程中，一般都采用能量法分析，从能量角度分析可以避免微分方程建立及求解过程中的复杂性，并且能够得到相对精确的近似解.

在集中荷载作用下，组合梁结构的总势能Π包括两部分：结构变形的应变能势能U与集中荷载作用的外力势能V，即

在组合梁结构中，压缩应变能和剪切应变能对于总体结构变形的影响很小，因此可以忽略.所以，导致结构侧向弯曲时的应变能为钢梁下翼缘的侧向弯曲应变能U1和腹板的侧向弯曲应变能U2两部分.假设工字钢梁下翼缘的侧向位移为uB，由材料力学知识［7］，结构应变能U1可表示为

在图1的正交坐标系中，忽略横向变形（x方向）以及结构中的剪切应变，梁腹板侧向屈曲的应变能可表示为

联立几何方程和物理方程，求解可得组梁结构侧向屈曲失稳的总应变能为

对于外力势能的计算，通过外力做功就可以直接得到，在数值上，二者相等，符号不同，即：

其中S1、S2、S3、S4为腹板变形能；S5为下翼缘的变形能；S6、S7为外力做功的能.

1.1.4 屈曲失稳的临界荷载

在计算组合梁结构侧向屈曲的临界荷载时，采用势能驻值原理［8］进行计算.势能驻值原理中，设势能变化为δП，则势能有驻值的条件为：

这是一个四阶非常系数齐次常微分方程，解起来有困难，因此采用半逆解法来对δΠ＝0进行求解，即根据边界条件来拟定方程解的形式，可求得临界荷载为

1.2 工字型钢－混凝土组合梁梁翼缘侧向弯扭失稳

1.2.1 弯扭失稳模型

构建组合梁结构的力学失稳模型时只考虑了钢梁下翼缘的侧向变形uB，并未考虑它的扭转变形.然而，当组合梁结构翼缘发生侧向屈曲时会伴随产生下翼缘的扭转变形φB，因此，建立集中荷载作用下组合梁翼缘侧向屈弯扭失稳模型如图3所示.

根据弹性力学知识，求解得到钢梁腹板的变形uW为

1.2.2 弯扭失稳势能

在集中荷载F的作用下，组合梁的侧向弯扭失稳势能主要包括三个部分，除翼缘的侧向弯曲应变能、腹板的侧向弯曲应变能外，还包括钢梁下翼缘的扭转变形应变能.根据上述类似的方法，可以求解得集中荷载作用下组合梁侧向弯扭失稳势能.

1.2.3 弯扭失稳的临界荷载

集中荷载作用下组合梁侧向弯扭失稳临界荷载求解方法与弯曲失稳求解方法相同，仍然采用势能驻值原理计算得到，在此不再赘述.

1.3 组合梁其它侧向失稳模型及计算

1.3.1 英国钢结构研究院方法

在计算组合梁结构失稳问题时，英国钢结构研究院在能量法的基础上开展创新.在计算时，它考虑了复变变形、截面扭转、侧向屈曲以及翼缘受压变形等四方面的组合梁变形，但是混凝土板变形以及支座的约束扭曲两部分变形被忽略了.求解得到极限弯矩之后，再根据实际组合梁结构的受力特点进行临界荷载的求解，具体的计算公式为

式中D为组合梁中钢梁截面高度；EIz为受压翼缘关于z轴的抗屈刚度.

1.3.2 弹性约束压杆的失稳模型

除了英国钢结构研究院采用的方法之外，文献［9］提到了弹性约束压杆的失稳模型计算方法.根据类比性，它将组合梁结构失稳变形转化到弹性压杆地基上.这种方法的缺陷在于，其失稳变形主要是取决于压杆的截面性质和两端的支承形式以及轴力的分布情况.其临界失稳压力的表达形式为

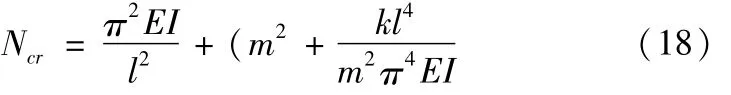
式中k为组合梁结构侧向弹性约束的约束刚度，m为杆长内失稳的波数.

2 算例分析

某多跨连续工字形组合梁的截面示意图如图4所示.若组合梁受到集中荷载作用，对其稳定性进行求解.其基本尺寸参数为：工字钢为I20a，混凝土翼板为C40现浇混凝土板，混凝土板厚hc＝120mm，混凝土板的有效宽度bc＝800mm，负屈矩跨度l＝4000mm.

图4 组合梁横截面尺寸

a.截面的几何性质

按相应计算方法得到如下结果：

（1）按集中荷载作用下工字钢下翼缘侧向弯曲失稳计算：组合梁屈曲时钢梁下翼缘侧向位移在l长度范围内的正弦半波数n＝400时，可得组合梁侧向弯曲失稳临界集中荷载值Fcr＝2.14×106N·mm.

（2）按集中荷载作用下工字钢下翼缘侧向弯扭失稳计算：组合梁屈曲时钢梁下翼缘侧向位移在l长度范围内的正弦半波数n＝190时，可得组合梁侧向弯扭失稳临界弯矩值Fcr＝1.89×106N·mm.

（3）按英国钢结构研究院的方法计算：得组合梁侧向失稳临界Mcr＝7.63×108N·mm，压杆截面面积可取等于工字钢截面面积之半A＝As／2＝1760.2mm2；所以组合梁侧向失稳临界弯矩值Ncr＝McrA／W＝2.92×106N·mm.

（4）按文献［10］介绍的方法计算：得临界压力Ncr＝1.55 ×106N·mm.

计算结果表明：

（1）在工字钢梁组合结构侧向稳定性分析过程中，下翼缘的扭转变形对整体组合梁结构变形是有影响的，需要考虑.运用弯曲失稳方法求解得到的临界荷载，忽略这一重要因素，求解得到的临界荷载较大，在实际设计中会导致整体结构提前发生失稳，偏于不安全.

（2）本文采用的方法与英国钢结构研究院的方法共同之处是将混凝土板看作完全刚性，不同之处在于前者是假定混凝土板和工字钢上翼缘不产生变形，并将腹板的变形用下翼缘的侧向变形和扭转变形表示；而后者考虑的是整个截面的圣维南扭转.从结果来看，后者的方法在设计上可能会导致组合梁提前出现侧向失稳的可能.

（3）文献［11］的方法引入了下半部腹板的面积，但是在负弯矩作用下组合梁弯曲时混凝土实际上已大部分开裂，此时截面的中性轴已然成为全部钢材的重心轴，截面的中性轴也高于工字钢梁截面的几何中性轴，它的应力值也应当随高度而发生变化.此外，该方法中没有考虑腹板对翼缘压杆的侧向惯性矩的影响，保守地将受压翼缘处理为弹性地基上压杆.

（4）本文建立的工字钢受压下翼缘侧向弯扭失稳模型，它不是将下翼缘等效为弹性压杆，而是同时考虑到了钢梁下翼缘的侧向变形和扭转变形和腹板的弯曲变形.这样就比文献［11］中方法相对更为可靠，比工字钢受压下翼缘侧向弯曲失稳模型更经济.

3 结论

对工字型钢－混凝土组合梁组合梁结构进行分析，基于材料力学、结构力学以及弹性力学知识，对两种组合梁结构侧向屈曲失稳问题进行了分析，通过理论计算得出了以下结论：

（1）根据集中荷载作用下工字型钢—混凝土组合梁变形特征，建立了集中荷载作用下组合梁翼缘侧向屈曲失稳的力学模型以及侧向弯扭力学模型.运用能量法，分别求解得到了两种模型的结构变形势能，并根据势能驻值原理，采用变分法，分别求解得到了两种模型下的临界荷载表达式.通过对两种模型进行分析，发现弯扭力学模型更加符合集中荷载作用下工字型钢—混凝土组合梁变形实际，符合工程实际要求；

（2）本文所建立的模型及计算的方法能够较好地反映模型受力变形的情况，特别是工字型钢—混凝土弯扭失稳模型，具有较高的计算精确度，因此计算公式具有较好的实用性.

［1］Narayanan R.Steel－concrete Composite Structures（Stability and Strength）［M］.Elsevier Applied Science，1988.

［2］Fukumoto Y，Kubo M.A Survey of tests on lateral buckling strength of beams［A］.2nd Int Colloquium Stability of Steel Structures［C］. 1997：233－240.

［3］Weston G，Nethercot D A.Lateral buckling in continuous composite bridges［J］.Structural Engineer，1991，（3）：79－87.

［4］Dekker N W.Factors influencing the composite beams with limited slip capacity of shear connections［J］.Journal of Structure Engineering，1995，（2）：127－130.

［5］British Standards Institution.Code of Practice for Design of Steel Bridge［Z］.BSI，1982.

［6］徐芝纶.弹性力学［M］.北京：高等教育出版社，1983.

［7］刘鸿文.材料力学［M］.北京：高等教育出版社，1992.

［8］夏志斌，潘有昌.结构稳定理论［M］.北京：高等教育出版社，1987.

［9］殷惠光，王景全，孙宝俊.钢－混凝土组合梁结构体系应用与研究进展［J］.彭城职业大学学报，2003，（5）：1－3.

［10］章荣国.新型T形截面外包钢混凝土组合梁滑移性能研究［D］.镇江：江苏大学硕士学位论文，2006.

［11］朱聘儒.钢－混凝土组合梁设计原理［M］.北京：中国建筑工业出版社，1989.

（责任编校：晴川）

Research on the Stability of I－shaped Steel－concrete Com posite Beam under the Action of Concentrated Load

BUWeifei
（Department of Mining and Construction Engineering，Jiangxi Polytechnic College，Pingxiang Jiangxi337000，China）

Steel－concrete composite beam structure is an important form of building structure in civil engineering construction，whose bearing capacity being effectively realized is of great significance for practical engineering.However，currently we do not have explicit standards and norms for the stability calculationmethod and structural design of steel－concrete composite beam structure，which brings about great inconvenience for the practice.The study verifies the calculationmethods for criticalbuckling under twomodels proposed in the paper through examples，and compares domestic and foreign calculation models and methods on the stability of composite beam，which verifies the feasibility of calculationmodels and methods.

steel－concrete composite beam；concentrated load；lateral buckling；critical load

TU398

A

1008－4681（2014）05－0027－04

2014－07－10

卜伟斐（1979－），女，山西晋中人，江西工业工程职业技术学院采矿与建筑工程系讲师，硕士.研究方向：钢筋混凝土组合梁稳定性.