双因素方差分析的应用及M atlab实现*
2014-10-10郭萍
郭 萍
(青岛理工大学琴岛学院,山东青岛 266106)
双因素方差分析的应用及M atlab实现*
郭 萍
(青岛理工大学琴岛学院,山东青岛 266106)
在阐述双因素方差分析原理的基础上,通过两个具体的数学建模案例,说明双因素方差分析的应用,并利用Matlab实现了两个案例的求解.在数理统计的授课过程中,将理论教学和数学软件Matlab紧密结合,不仅能帮助学生深入理解双因素方差分析的原理,而且能激发学生学习和研究的兴趣,提高学生自己动手分析、解决问题的能力,明显提高了课堂的教学效率和效果.
双因素方差分析;数理统计;应用;Matlab
当今社会是一个信息高度发达、人们的社会经济活动日益频繁的社会,大量的信息、数据需要人们处理.如何从这些海量的信息中提取有用的信息,指导人们的社会实践活动,越发显得必要而迫切,这为数理统计提供了日益广阔的舞台[1].
方差分析是数理统计中非常重要的一节,方差分析又称“变异数分析”或“F检验”,是由R.A.Fisher发明的,用于对两个及两个以上样本均数差别的显著性检验[2].双因素方差分析是检验在两种因素影响下,两个以上总体的均值彼此是否相等的一种统计方法.由于双因素方差分析的原理抽象,计算繁琐,导致教学枯燥无味.基于此,文中阐述了双因素方差分析的原理,通过两个具体的数学建模案例,说明双因素方差分析的应用,并利用Matlab实现了两个案例的求解.在数理统计的授课过程中,这种从理论到应用,再从应用到上机实现的过程,让学生体会到“学以致用”的真正含义,激发了学生的学习兴趣,同时也提高了学生的动手能力.
1 无交互影响的双因素方差分析
1.1 无交互影响的双因素方差分析原理
设因素A取r个水平,分别记为A1,A2,…,Ar,因素B取 s个水平,分别记为B1,B2,…,Bs,组合(Ai,Bj)下总体Xij~N(μij,σ2) i=1,2,…,r j=1,2,…,s,由此可得,无交互影响的双因素方差分析表(表1).
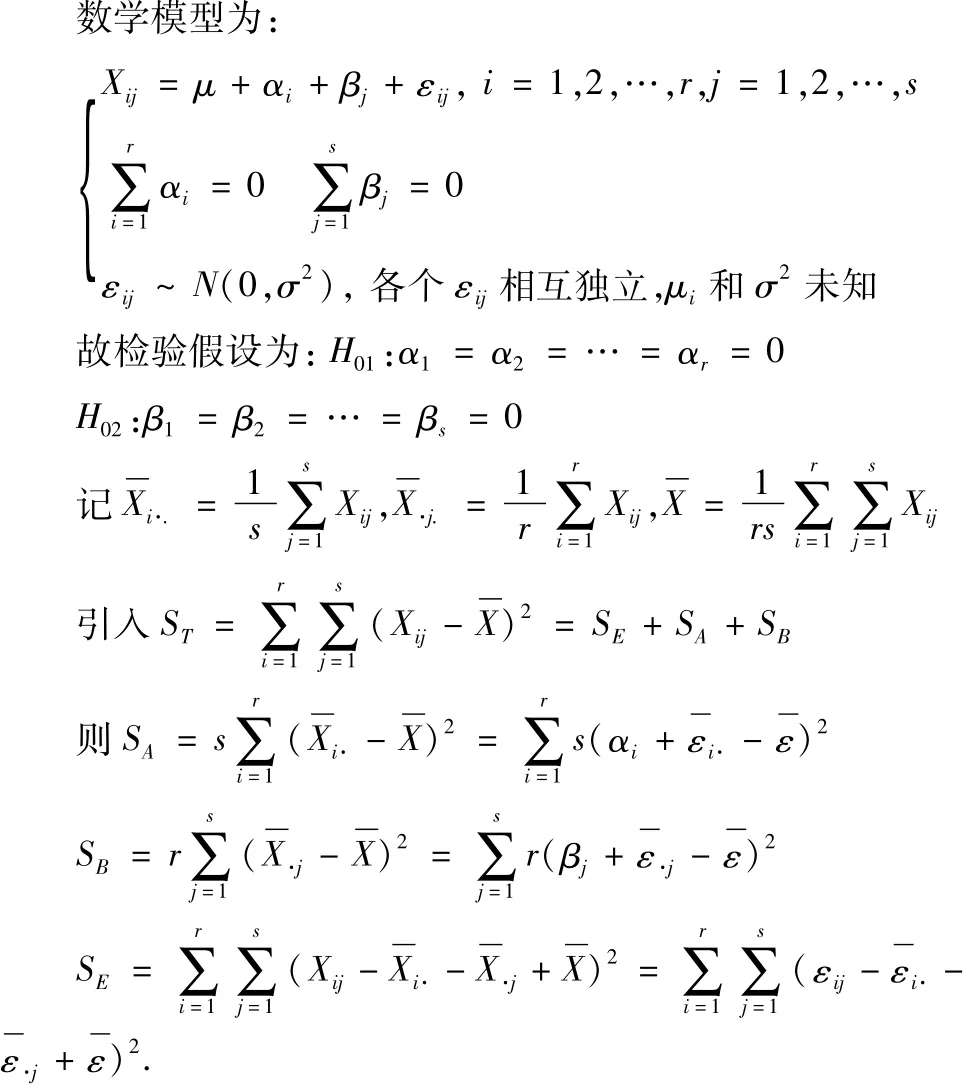
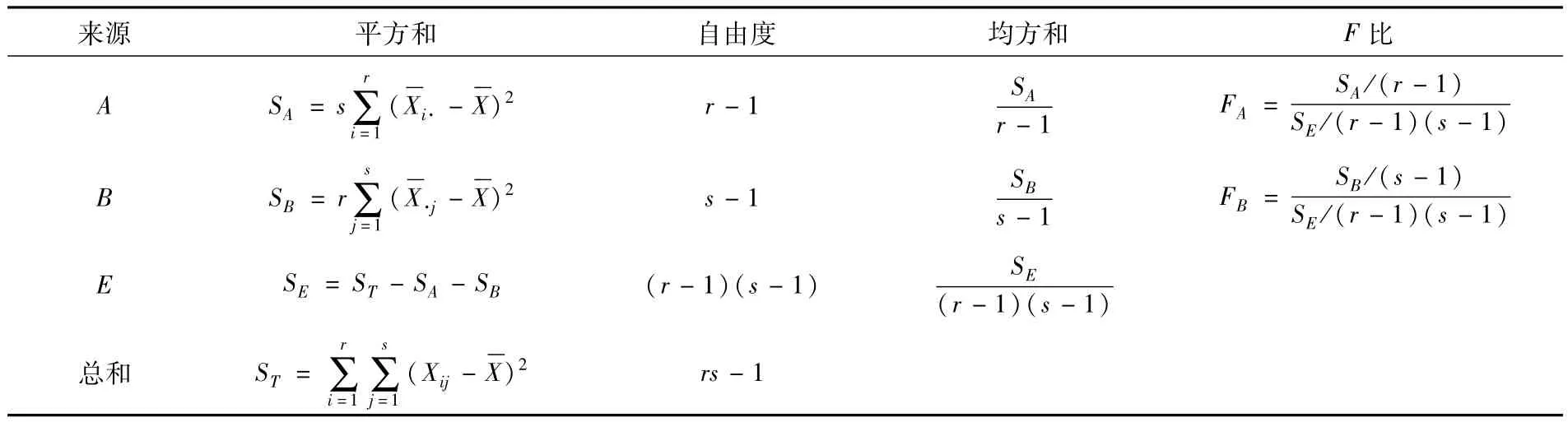
表1 无交互影响的双因素方差分析表[3]
检验规则为:
(1)若FA>F1-a(r-1,(r-1)(s-1))时,则拒绝H01,表示因素A的各水平下的效应有显著差异;
(2)若FB>F1-a(s-1,(r-1)(s-1))时,则拒绝H02,表示因素B的各水平下的效应有显著差异.
1.2 Matlab实现
统计工具箱中用anova2作双因素方差分析.无交互影响的双因素方差分析命令为[p,t]=anova2(x),返回值p是两个概率,当p>α时接受H0,t是方差分析表.
1.3 案例1
三位操作工分别在四台不同的机器上操作一天的日产量(如表2所示).

表2 三位操作工分别在四台不同的机器上操作一天的日产量
试在显著性水平α=0.05下检验:
(1)操作工之间的差异是否显著?
(2)机器之间的差异是否显著?解:编写程序如下:

求得p=0.6912、0.9932,第一个p值是由列因素(即操作工)影响下得到的,第二个p值是由行因素(即机器)影响下得到的,由于两个p值均大于0.05,故接受原假设,说明操作工之间,机器之间均无显著差异.
2 有无交互影响的双因素方差分析
2.1 有交互影响的双因素方差分析原理

由此可得,有交互影响的双因素方差分析表(表3).

表3 有交互影响的双因素方差分析表[3]
检验规则为:
(1)若FA>F1-a(r-1,rs(t-1))时,则拒绝H01,表示因素A的各水平下的效应有显著差异;
(2)若FB>F1-a(s-1,rs(t-1))时,则拒绝H02,表示因素B的各水平下的效应有显著差异.
(3)若FA×B>F1-a((r-1)(s-1),rs(t-1))时,则拒绝H03,表示因素A与因素B的交互作用显著.
2.2 Matlab实现
统计工具箱中用anova2作双因素方差分析.有交互影响的双因素方差分析命令为[p,t]=anova2(x,reps),返回值p是三个概率,当p>α时接受H0,t是方差分析表.
2.3 案例2
三位操作工分别在四台不同的机器上操作三天的日产量(如表4所示).

表4 三位操作工分别在四台不同的机器上操作三天的日产量
试在显著性水平α=0.05下检验:
(1)操作工之间的差异是否显著?
(2)机器之间的差异是否显著?
(3)操作工和机器的交互作用是否显著?解:编写程序如下:


求得p=0.0023、0.6645、0.0002,第一个p值是由列因素(即操作工)影响下得到的,第二个p值是由行因素(即机器)影响下得到的,第三个p值是由机器与操作工交互影响下得到的,由于第一个和第三个p值均小于0.05,故拒绝原假设,而第二个p值大于0.05,故接受原假设,说明在α=0.05水平上,操作工有显著差异,机器之间无显著差异,交互作用有显著差异.又由于第三个p值小于0.01,说明交互作用有非常显著差异.因此,要想提高日产量,一是要提高工人的技能,二是工人要操作自己最熟练的机器.
3 结语
目前统计工作所面临的数据日益庞大,传统教学中的计算公式已经很难使用手工计算的方式进行求解,因此借助于计算机及matlab软件完成统计计算,分析统计结果,做出统计推断便成为数理统计教学中不可忽视的一个手段[4].
在实际授课过程中,将理论知识条理化,扩充一些理论与实际相结合的例子,对于较复杂的计算方法利用matlab实现,不仅可以促进学生对理论知识的理解,让学生深刻体会到理论在实际中的应用,而且可以加强学生的动手操作能力,从而激发学生学习兴趣,更有利于实现应用型人才的培养目标.
[1]夏传武.Matlab在概率统计教学中的应用[J].徐州工程学院学报,2005,(S1):96-98.
[2]易昆南,程勋杰.“假设检验”决策的误区——一场由全国大学生数学建模竞赛引发的争论[J].重庆理工大学学报(自然科学版),2013,(4):106-109.
[3]魏宗舒.概率论与数理统计教程[M].北京:高等教育出版社,2001.
[4]王宁,孙晓玲.概率论与数理统计实验教学案例设计及实现[J].合肥师范学院学报,2014,(3):69-72.
(责任编校:晴川)
App lication of Two Factor Analysis of variance and Its Realization w ith M atlab
GUO Ping
(Qindao College,Qingdao University of Technology,Qingdao Shandong 266106,China)
Based on the introduction of the principle of two factor analysis of variance and two specific cases ofmathematicalmodeling,the paper demonstrates the application of two factor analysis of variance,and uses Matlab to solve two cases.In the teaching process of mathematical statistics,combining theory teaching andmathematics software Matlab can notonly help students understand the principle of two factor analysis of variance,but also stimulate students’interests in learning and research,and improve their ability in analyzing and solving problems,which improves the efficiency and effects of the teaching.
two factor analysis of variance;mathematical statistics;application;Matlab
O29
A
1008-4681(2014)05-0138-03
2014-09-11
郭萍(1981-),女,山西阳泉人,青岛理工大学琴岛学院讲师,硕士.研究方向:概率论、数理统计、动力系统.
