基于稀疏恢复的空时二维自适应处理技术研究现状

马泽强 王希勤 刘一民 孟华东

(清华大学电子工程系 北京 100084)

1 引言

稀疏恢复(Sparse Recovery,SR)是信号处理领域近年来兴起的一个研究热点[1－6]，主要关注具有稀疏性的信号。信号的稀疏性是指当用一个1维向量表示信号时，信号向量中绝大多数位置的元素值等于零或十分接近零，只有少数位置的元素有显著值，这样的信号被称为稀疏信号。稀疏恢复的主要思想是：在信号处理领域的很多场景中，信号向量往往本身具有稀疏性，或在某种变换之下具有稀疏性，对于稀疏信号，可以通过一定的方法进行压缩观测，使原来维度较大的信号以较小维度存储，当压缩观测满足一定条件时，可以通过相应的算法从压缩观测信号中恢复出原始的维度较大的稀疏信号，这一过程就叫做稀疏恢复。

稀疏恢复理论的数学模型可以用一个欠定线性方程组y=Ax的求解来说明，其中y为M×1的观测信号，A为M×N的观测矩阵(也称为基矩阵)，其中M＜N，矩阵A的每一列可以认为是一组基中的一个基向量。x为N×1的待恢复的稀疏信号向量。原始的稀疏恢复问题目标是求出“最稀疏”的原始信号向量，即使信号向量中显著分量数目最少，所以可以建模为一个l0范数最小化问题(l0范数定义为向量中非零元素的数目)：

其中ε为噪声容限。由于 l0范数最小化问题是一个非凸优化问题，直接求解的难度较大，所以很多情况下可以将该优化问题转化为如式(2)所示的 l1范数最小化问题[6]：

在雷达信号处理领域，有许多场景会涉及到通过较少的观测估计高分辨信号的问题，比如 SAR/ISAR成像、DOA/空间谱估计、自适应阵列处理、空时2维自适应处理等。在一定的变换下，这些待估计的信号具有稀疏性。目前国内外已经有大量学者开展了将稀疏恢复应用到雷达信号处理中的研究。

空时 2维自适应处理(Space-Time Adaptive Processing,STAP)技术是机载阵列雷达中一种重要的信号处理手段，其主要作用是抑制地杂波，检测慢速小目标[8]。传统的STAP技术需要通过距离维上足量的独立同分布的平稳训练样本来获得对杂波协方差矩阵的估计：

Reed等人的研究表明，如果阵元数为N，一个相干处理间隔(CPI)内的相干脉冲数为 M，那么当独立同分布训练样本数L＞2MN时，该方法可以获得近似最优性能。而在实际场景中，即使经过子阵合成，雷达的阵元数N和相干脉冲数M也是较大的，所以往往很难得到满足这一要求的足量平稳训练样本。为了减少所需的训练样本数，研究者提出了许多降维或降秩的STAP算法，以及直接数据域STAP方法。但这些方法在降低所需样本数的同时，往往会减小等效孔径的大小，造成性能损失。所以，在杂波非均匀环境下，如何通过较少量的平稳训练样本获得对杂波的尽可能准确的估计，是STAP技术面临的一个重要问题。

图1 传统STAP方法与空时谱估计-滤波器结构SR-STAP方法示意图Fig.1 The block diagram of traditional STAP method and SR-STAP

稀疏恢复在小样本下的优势和STAP技术面临的上述问题促使了基于稀疏恢复的 STAP技术(Sparse Recovery-based STAP，以下简称稀疏恢复STAP技术或SR-STAP)的出现。目前已经取得一定研究成果的稀疏恢复STAP技术是基于空时谱稀疏性的空时谱估计-滤波器结构 SR-STAP方法[9]，本文主要对基于空时谱稀疏性的稀疏恢复STAP方法的已有研究成果进行总结，并对其中涉及到的其他一些研究方向进行简要探讨。

2 基于空时谱稀疏性的SR-STAP方法

2.1 谱估计-滤波器结构SR-STAP的基本框架

传统的STAP算法可以分为两个环节：即估计杂波特性(具体体现在对杂波协方差矩阵的估计上)和自适应滤波。估计杂波协方差矩阵是通过直接将训练样本的自相关矩阵求平均得到的，如图1中“传统STAP方法”对应的实线框内流程所示。

2009年，文献[9]最先提出了正侧视均匀线性阵列(ULA)情形下基于稀疏恢复的STAP方法，该方法先利用稀疏恢复对检测单元杂波的空时谱进行估计，然后利用空时谱来估计杂波协方差矩阵。在这里我们将这种方法称为谱估计-滤波器结构的SR-STAP方法，如图 1中“谱估计-滤波器结构SR-STAP方法”对应的实线框内流程所示。其基本结构和传统的STAP方法一样，依然是使用检测单元附近的训练样本来估计杂波协方差矩阵，然后做自适应滤波。两者的核心差别在于利用采样数据估计杂波协方差矩阵的方法，即图1中虚线框内所示的部分。

谱估计-滤波器结构的SR-STAP方法是基于杂波空时谱的稀疏性建立的。如图2所示，对于某一距离单元的采样数据(以下称为空时快拍)，如果对其做2维DFT变换，会得到多普勒频率-波达角域的2维空时谱。由于机载雷达平台的运动，地杂波散射源相对雷达会有一定的运动速度，那么杂波的多普勒频率和波达角之间会有线性的关系fd=2v/ λ sin θ ，在空时谱平面上表现为一条斜线，称之为杂波脊线。图2为MountainTop数据146#距离单元的杂波空时谱，可以看出呈现稀疏特性。

理论和实验都表明，杂波脊线在整个空时谱平面上占据较窄的一条“频带”[9]，将空时谱做向量化后得到一个稀疏向量，只有少数位置的元素有显著值，对应杂波散射源，其他大部分位置都接近零，只有噪声分量。这是利用稀疏恢复进行杂波空时谱估计的重要前提和保证。在向量化的空时快拍x和向量化的空时谱α之间，存在着一个线性变换：

其中，n为观测噪声向量，Φ为空时导引矢量t排列组成的基矩阵，因为该基矩阵是在一个完备的正交基矩阵基础上扩充得到的，其列向量组构成了一组超完备基，所以又称为超完备基矩阵：

其中Ns=ρsN是角度维的量化点数，Nd=ρdM是多普勒维的量化点数，其中ρs和ρd分别为空时谱估计时角度维和多普勒维的扩维系数。式(4)是一个典型的稀疏恢复问题的模型，可以使用稀疏恢复的方法求解。因此，空时谱估计的问题就转化为如式(6)所示的一个稀疏恢复问题：

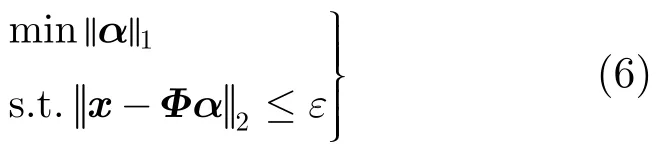
这里将稀疏恢复问题建模为l1范数最小化问题，通过求解这个稀疏恢复问题，可以获得空时谱估计α。通过稀疏恢复估计空时谱的过程如图3所示。

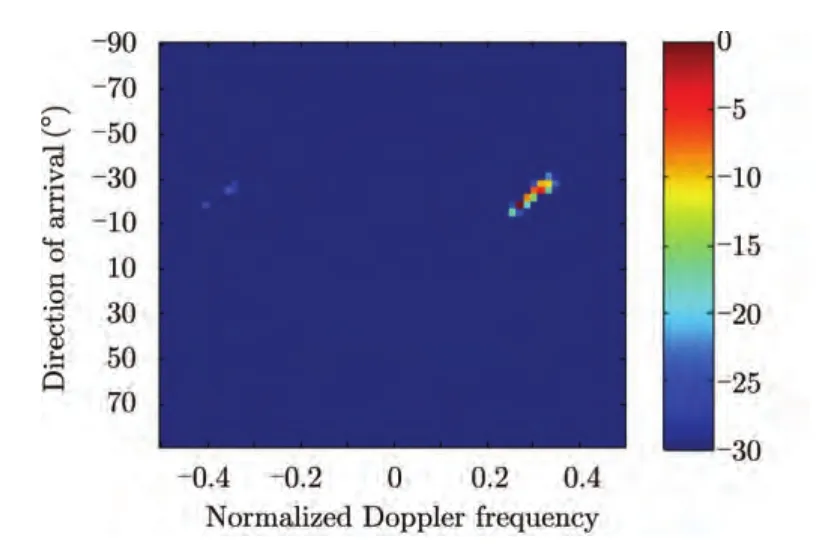
图2 杂波空时谱稀疏性示意图Fig.2 The sparsity of clutter space-time spectrum

图3 利用稀疏恢复进行杂波空时谱估计示意Fig.3 Estimating clutter space-time spectrum using sparse recovery

另外一个十分重要的环节是建立起空时谱和杂波协方差矩阵之间的联系，由式(4)以及杂波协方差矩阵的定义，Rxx=E[x xH]=E[ΦααHΦH]=Φ E[ααH]ΦH，可以得到式(7)所示的通过空时谱来估计杂波协方差矩阵的公式：

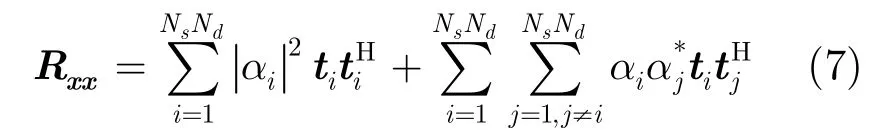
式(4)～式(7)是谱估计-滤波器结构的 SRSTAP方法的核心环节，即利用稀疏恢复从空时快拍x得到杂波协方差矩阵估计Rxx的完整流程。得到杂波协方差矩阵估计后的处理方法和传统STAP方法一致，即构造自适应滤波器：

整个方法的流程如图1中“谱估计-滤波器结构STAP方法”对应的实线框内所示。在该方法中，估计空时谱所用的仍然是来自检测单元附近距离单元上的训练样本，因此需要假设在检测单元邻近的若干个距离单元内，杂波满足局部平稳，即局部范围内能够获得若干个满足独立同分布的训练样本。在这种条件下，采用了稀疏恢复的直接优势就是能够使用很少的训练样本，就获得和传统方法接近甚至更优的性能。

有多种谱估计方法可以实现从空时快拍得到空时谱估计，比如2维DFT,MUSIC,Capon等方法。相比稀疏恢复空时谱估计方法，这些方法都有明显的不足，比如 DFT高旁瓣且分辨力受限于孔径大小(即采样数据维度)，Capon和MUSIC等传统高分辨谱估计方法则需要足量的快拍才能工作。相比这些传统谱估计方法，稀疏恢复的重要优势是，只需少量快拍即可实现高分辨的空时谱估计，进而获得对杂波特性的较好估计。

STAP方法的最终性能体现在杂波抑制效果上。在自适应滤波器的构造方法相同的情况下，杂波协方差矩阵估计的质量就成为了决定算法性能的关键因素。相关实验结果说明，用稀疏恢复空时谱估计得到的杂波协方差矩阵的估计具有优良的性能。图4展示了在MountainTop数据上传统STAP方法和谱估计-滤波器结构的 SR-STAP方法的性能对比。图4(a)，图4(b)两图通过空时谱输出结果的对比说明了SR-STAP具有更好的杂波抑制和目标检测性能，图4(c)的结果证明了SR-STAP可有效抑制主杂波，使得最大的旁瓣杂波剩余比实际运动目标低 8 dB左右。而利用同样数据训练样本传统方法难以有效估计出实际杂波分布，因此经过传统方法杂波抑制，目标还淹没在周围杂波剩余中，无法检测出。

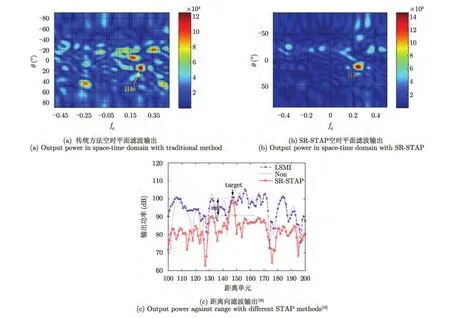
图4 传统STAP方法与空时谱估计-滤波器结构SR-STAP方法性能对比Fig.4 Performance comparison between traditional STAP methods and SR-STAP

从数学角度来看，谱估计-滤波器结构的 SRSTAP方法的基本框架和传统 STAP方法是一致的。如果将STAP看做一个优化问题，其优化的目标都是最大化输出信杂比SCNRout，由这个优化目标推导出来的最优滤波器的形式都是 w=，所以问题的关键是获得尽可能精准的杂波协方差矩阵的估计。谱估计-滤波器结构的SR-STAP方法的核心创新之处就在于避免了传统方法使用大量样本训练协方差矩阵的做法，将协方差矩阵的估计转化为一个空时谱估计问题，并使用稀疏恢复方法求解。在这种框架下，提高SR-STAP性能的关键也就在于尽可能将杂波协方差矩阵Rxx估计准确，即尽可能将杂波空时谱估计准确。

下面对谱估计-滤波器结构的SR-STAP框架下国内外近年来的一些研究成果进行简要介绍。

2.2 off-grid问题

谱估计-滤波器结构的SR-STAP方法面临着傅里叶基矩阵下稀疏恢复的一个共有问题：格子对不准问题(off-grid)[11]，有些文献也称之为基失配问题(basis mismatch)[12,13]。在基于稀疏恢复的空时谱估计中，该问题描述如下：在构造稀疏恢复问题的超完备基矩阵Φ时，需要将空时导引矢量的两个参数，即杂波的多普勒频率和波达角，进行离散化(格点划分)。而真实回波中杂波的这两个参数往往难以完全和预先划分的参数格点严格对齐，这就是off-grid问题。图5对空时谱估计中的off-grid问题进行了示意。图5中“空时频点”指多普勒频率-波达角对。

在谱估计-滤波器结构的SR-STAP方法中，offgrid会显著影响空时谱估计的性能，进而引起杂波抑制效果的下降，所以研究针对 off-grid问题的稀疏恢复算法，对于提高谱估计-滤波器结构的SR-STAP算法的性能很有意义。减少或消除off-grid问题带来的影响，一个最自然的思路就是设计自适应方法，寻找真实的基矩阵，即寻找杂波真实的多普勒频率和波达角。

国外已经有学者展开了对这一课题的研究。在2013年IEEE雷达会上出现了相关的论文[14]，提出了一种基于字典学习(dictionary learning)的稀疏恢复杂波空时谱估计方法CSDL算法。对于存在offgrid的基矩阵，假设在某个格点上构造的多普勒频率和波达角分别为fi和θi，真实杂波对应的多普勒频率和波达角分别为 fi+Δfi和 θi+Δθi，则真实的基矩阵中对应的那一列导引矢量为：

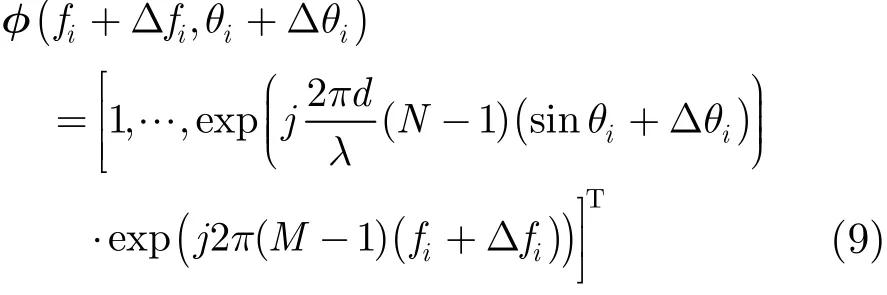
那么，考虑了格点失配之后的稀疏恢复空时谱估计问题变为：

其中基矩阵Φm为式(9)中包含格点误差在内的空时导引矢量构成的基矩阵，Δα为空时谱估计的误差。估计真实的基矩阵等效于估计空时频点的误差Δfi和Δθi，以及空时谱估计α和估计误差Δα，建立以它们为优化变量的优化问题：

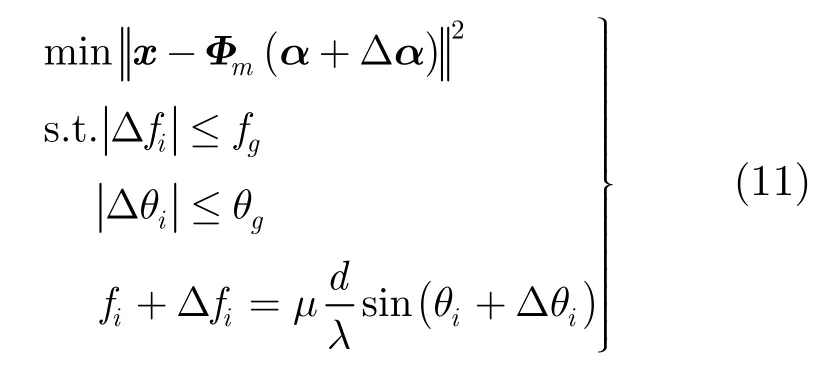
其中fg和θg是对格点误差范围的限定，最后一个约束是限定多普勒频率和波达角之间满足杂波脊线的线性关系。优化问题的求解在α,Δα和Δfi,Δθi之间交替进行：初始化时假设没有格点误差，得到关于空时谱α的初始估计，然后固定α和Δα，求解优化问题式(11)得到Δfi,Δθi的估计；再利用Δfi,Δθi的估计构造基矩阵Φm，再求解式(10)的稀疏恢复问题得到α,Δα的估计。如此交替进行，直至满足收敛条件。

文献[14]展示了该算法在KASSPER数据上的实验结果，以归一化输出信杂噪比SINR为指标，如图6所示。

图5 空时谱估计中格子对不准问题示意Fig.5 The off-grid problem in space-time spectrum estimation

图6 CSDL算法性能展示[14]Fig.6 Performance of CSDL algorithm[14]

根据该文献展示的实验结果，基于字典学习的CSDL算法能够有效解决off-grid问题，估计出杂波在空时谱平面上的真实位置，具有较好的鲁棒性。

2.3 MMV问题

在谱估计-滤波器结构的SR-STAP方法中，有一类问题叫做多观测向量问题(Multiple Measurement Vector,MMV)[15,16]，该问题表述如下：在杂波局部平稳条件下，可以得到距离维上若干个快拍的平稳训练样本，在此条件下使用稀疏恢复做空时谱估计，需要研究如何联合这多个快拍进行稀疏恢复才能充分利用多快拍中的信息，提高空时谱估计的精度和杂波抑制性能。

在2013年IEEE雷达会上发表了对该问题研究成果[17]，建立了混合l2,1范数优化模型[18]来求解联合稀疏恢复空时谱估计问题。在多快拍情形下，假设L个快拍组成的观测数据矩阵为 X=[x1,x2,…,xL]，联合稀疏恢复所得空时谱估计的结果组成的矩阵为A=[α1,α2,…,αL]，基矩阵仍然为 Φ ，那么多快拍情形下联合稀疏恢复的数学模型为：

其中，N 为观测噪声矩阵。求解该问题的混合 l2,1范数优化模型为：

其中混合l2,1范数为先对A的每一行求l2范数得到一个列向量，再对这个列向量求l1范数。对于稀疏恢复MMV问题，基本的假设是：多个观测向量xi来自同一个随机过程；它们都在同一个基矩阵下呈现稀疏特性，且这些稀疏向量αi具有相同的支撑集(即显著元素的位置)，并且显著元素的幅度服从同一随机分布。“不同快拍对应的稀疏空时谱具有相同的支撑集”这一假设是多快拍联合稀疏恢复能够进行的基本前提，在这个假设下，最小化混合l2,1范数的物理意义就很明显：l2范数对稀疏向量本身的稀疏性并无影响，但可以通过l2范数将稀疏约束在不同快拍间互相增强，l1范数保证了稀疏性的约束。通过混合l2,1范数，多快拍中蕴含的支撑集位置的信息被充分挖掘，提高了稀疏恢复估计支撑集位置的准确度[17,18]。

可以证明，式(13)仍然是一个凸优化问题，可以用凸优化算法求解。在联合稀疏恢复的结果A求得后，可以通过对行求l2范数获得最终的稀疏谱估计。图7展示了该方法在仿真数据下的实验结果。

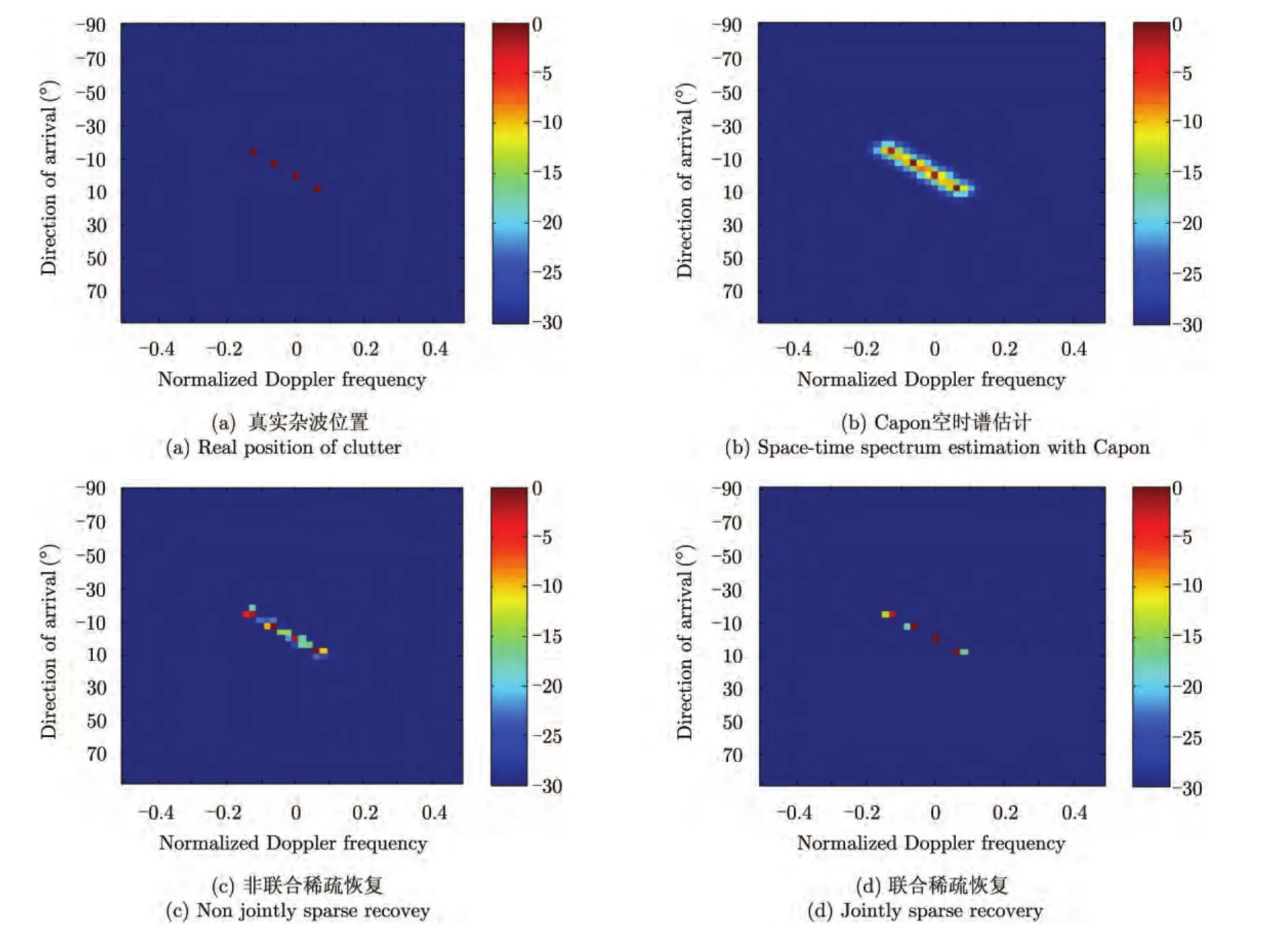
图7 联合稀疏恢复空时谱估计实验结果[17]Fig.7 Space-time spectrum estimation with jointly sparse recovery[17]

对于混合 l2,1范数优化问题还可以做一步的研究，比如在空时谱估计问题中该凸优化问题的针对性求解方法、多快拍情形下涉及阵列误差和 offgrid问题时的自适应联合稀疏恢复等。

2.4 共型阵问题

共型阵(ConFormal Array,CFA)配置在飞机机身、机翼或机头等部位，其形状和所配置部位的机体形状一致，具有载荷重量小、孔径数大、观测范围广等优点，因此研究共型阵下的STAP方法也具有重要意义[19－21]。共型阵条件下，杂波空时谱中波达角和多普勒频率不再成线性关系，并且随着距离变化。因此利用检测单元附近的训练样本估计的杂波协方差矩阵和真实杂波协方差矩阵特性并不一致，导致自适应滤波器的杂波抑制性能下降。针对随距离变化的杂波场景，已经有若干方法出现，其中基于距离配准补偿的 RBC算法就是较有代表性的一种[22,23]。该方法首先估计机载雷达平台的参数信息以及杂波场景的散射强度分布，然后设计变换矩阵以使得经过处理后的训练样本和检测单元配准。RBC算法可以同时实现主瓣和旁瓣杂波的有效补偿，但由于 RBC基于子孔径做空时谱估计，因此性能受限，限制后续配准处理的性能。

文献[24,25]最早将稀疏恢复引入了共型阵列的STAP方法研究之中，提出了基于RBC算法和稀疏恢复的SR-RBC方法，将平台参数估计和杂波估计统一在稀疏恢复环节中解决，并且该方法基于完整孔径估计，没有系统自由度(Degree Of Freedom,DOF)损失，谱估计性能较好，鲁棒性也较高。

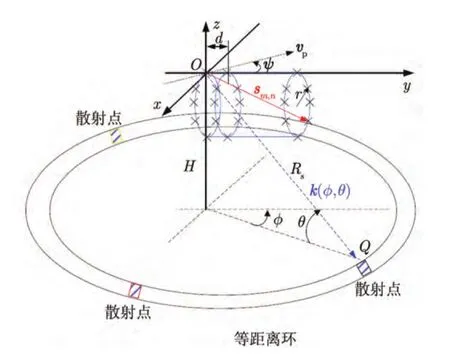
图8 机载圆柱体共型阵列示意[10]Fig.8 Airborne cylindrical arrays[10]

SR-RBC方法建立在如下的基本共型阵模型上：如图8所示，假设x,y和z轴分别代表正北、正西和垂直地球表面的方向；共型阵为圆柱形阵列，由M个圆形阵列环组成，圆环阵列和y轴垂直且均匀平行排列，每个圆形阵列中有N个均匀分布的阵元。对于地面上静止的杂波散射源Q，其空间方位角和俯仰角分别为φ和θ，记为角度向量Ψ=[φ,θ]T，电磁波的方向向量记为k(Ψ)，那么空域导引矢量和时域导引矢量分别为：

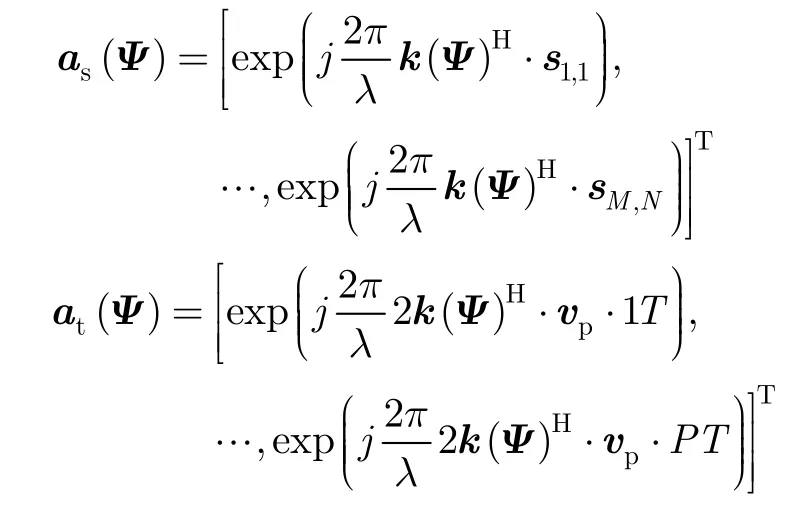
其中sm,n表示第m个阵列环的第n个阵元的方向向量，vp代表载机运动速度矢量，P为CPI内相干脉冲数。那么，在不考虑距离模糊、阵列误差的情况下，第 k个距离环的回波数据可以表示为：xk=。其中是第k个距离单元上第q个杂波散射源对应的空时导引矢量，αq,k代表第k个距离单元上第q个杂波散射源的散射强度。需要注意的是，不同于正侧视ULA阵列，在共型阵条件下，杂波散射源的空时导引矢量不仅与其所在方位角有关，而且和距离相关，同样的方位角上不同距离环上的杂波散射源对应的空时导引矢量也是不同的。所以，对于不同的距离单元k，需要构造不同的超完备基矩阵kΦ。对于整个圆柱体阵列来讲，其等效孔径维度为NM，而CPI内相干脉冲数为P，所以对多普勒频率-波达角参数平面量化为 Ns=ρsNM,Nd=ρdP，量化之后的多普勒频率-波达角对表示为(fi,φj)。那么，第k个距离单元的回波数据可用如式(14)方程表示：

在利用稀疏恢复方法得到高分辨的空时谱估计之后，和传统 RBC方法一样，还可以进一步设计变换矩阵，对不同距离单元的回波数据进行距离配准。传统 RBC方法通过子孔径平滑获得多个低维度的子孔径，进而利用 Capon等方法获得频谱估计，所以性能有一定的损失。传统 RBC方法采取提取频谱主要分量估计平台参数，进而估计杂波散射源散射强度的方法。SR-RBC方法将空时谱估计和平台参数估计结合在一起，并且空时谱估计是基于完整孔径的，没有系统自由度损失，谱估计性能更好。

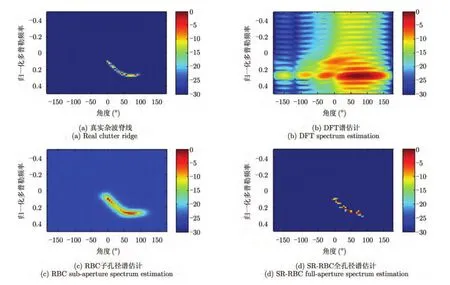
图9 SR-RBC空时谱估计性能[24]Fig.9 Perfoamance of space-time spectrum estimation with SR-RBC[24]

文献[24]给出了非正侧视共型阵的实验结果，如图9所示。图中结果说明，SR-RBC由于利用了全孔径，可以得到分辨率更高、精度更高的谱估计。

图10 SR-RBC改善因子性能[24]Fig.10 The improvement factor of SR-RBC[24]

图10表明，在共型阵条件下，由于不同距离单元的杂波特性并不一致，传统的LSMI算法估计的杂波凹口位置不准，性能下降严重；RBC算法和SR-RBC算法都可以实现杂波脊线主瓣和旁瓣的配准以及抑制，但由于 RBC的平台参数和杂波特性估计都是基于子孔径的，所以有一定的性能损失。而SR-RBC算法是基于全孔径的，没有孔径损失，并且是直接基于快拍数据的估计。总体来看，在共型阵条件下，由于不同距离单元的杂波特性完全不同，因此基于稀疏恢复的STAP方法具有巨大的优势和潜力。共型阵的具体形式多种多样，针对不同的共型阵形式开展基于稀疏恢复的STAP方法的针对性研究也是很有意义的。

2.5 直接数据域SR-STAP

前面所介绍的空时谱估计-滤波器结构的 SRSTAP方法都是基于训练样本的，即对杂波特性的估计是基于检测单元邻近距离单元的训练样本完成的。在杂波极度非均匀、非正侧视阵列、共型阵列等条件下，训练样本的杂波特性和检测单元的杂波特性会有较大差别，因此基于训练样本的STAP方法总是面临着检测单元杂波特性难以精准估计的问题。为此，人们提出了基于检测单元采样数据对检测单元本身的杂波特性进行估计的方法，这就是直接数据域STAP方法[26,27]。

经典的直接数据域方法一般采用滑动子孔径方法。比如D3LS方法[26,28]，假设在正侧视ULA阵列下，阵元数和一个 CPI内的相干脉冲数分别为 N和M，并且假设关心的目标的多普勒频率和角度的大致位置已知(在实际中这一点是可能实现的，可以根据其他传感器预先获知感兴趣目标的大致位置)，D3LS方法选择一个小于原始孔径维度的子孔径，沿着采样空时快拍数据矩阵滑动处理，对目标所在的多普勒频率-波达角，在相邻的两个子孔径间对消，然后将子孔径样本进行合成处理，进而获得自适应滤波器。D3LS方法虽然可以在一定程度上消除潜在目标的影响，获得不含潜在目标的杂波特性的估计，但这是以牺牲孔径维度为代价的，子孔径的维度小于原始孔径维度，导致分辨能力下降，对杂波特性的估计精度下降。

针对D3LS方法的不足，文献[29]提出了基于稀疏恢复的直接数据域STAP方法，称作D3SR方法。该方法假设阵列为非正侧视ULA阵列(正侧视只是非正侧视的一个特例，该方法仍然适用)，并且假设感兴趣目标所在空时平面上的区域(SOI)已知。在非正侧视情形下，杂波空时谱为一系列的椭圆脊线，并且不同距离环上的椭圆杂波脊线并不重合。

D3SR方法首先利用稀疏恢复对检测单元做高分辨的空时谱估计，假设检测单元采样数据为x，和基于训练样本的谱估计-滤波器结构SR-STAP方法一样，用空时导引矢量构造超完备基矩阵Φ，那么，对向量化的空时谱α的估计就转化为求解如式(15)所示的欠定方程：

理论和实验都表明，在非正侧视情形下，杂波在空时平面上表现为一系列的椭圆脊线(正侧视情形下退化为线性关系)，杂波显著分量在空时平面上占据的比例很小，所以杂波的空时谱α满足稀疏性，方程式(15)可以使用稀疏恢复的方法求解。在文献[29]所提的 D3SR方法中，使用了一种针对该方法进行修正和改进的 FOCUSS算法来求解该稀疏恢复问题，具体过程在这里不详述。

直接从检测单元得到的高分辨的空时谱估计准确反映了检测单元的杂波特性，比使用邻近距离单元训练样本得到的空时谱估计可信度更高。由于一般情况下信杂比较低，目标被杂波所淹没，很难直接提取出来，所以直接在检测单元空时谱估计上做检测的想法并不十分可行。D3SR方法采取了利用空时谱估计构造自适应滤波器的方法。由于空时谱估计中可能包含潜在目标，所以如果直接用该空时谱来估计杂波协方差矩阵，很可能在自适应滤波的时候将目标也抵消掉。为了避免这种情况发生，必须使用潜在目标空时位置的先验信息。假设我们已经从先验信息中获得目标 SOI区域的大致估计Γ(θs,fd)，那么，我们使用去除了区域Γ的空时谱分量来估计杂波协方差矩阵：

图11展示了在非正侧视情形下D3SR方法与D3LS方法的性能对比，可以看到，D3SR方法由于利用了全孔径，空时谱估计性能更佳，所以构造的自适应滤波器性能也更优。滤波之后空时平面的输出中，杂波脊线已经基本被完全消除(图11(b))，而D3LS方法由于利用子孔径滑动导致谱估计性能的损失，其滤波输出中杂波分量还有明显残余(图11(a))。距离维的滤波输出和改善因子也证明了D3SR方法的优势。

D3SR方法不需要训练样本即可有效估计检测单元的杂波特性，有效避免了训练样本和检测单元失配的影响，在杂波环境剧烈变化或非正侧视情形下具有明显优势和很好的应用潜力。直接数据域SR-STAP中还涉及到一些问题，例如获得潜在目标区域先验信息的有效方法、D3SR方法潜在的快速算法等，都值得进一步深入研究。

3 有待进一步研究的问题

从信号处理结构的角度，如果把STAP方法看作一个系统，其输入是空时2维的观测数据，其输出是滤波之后的空时 2维频谱(或主波束方向的多普勒频谱)，通过深入分析 STAP技术的本质和算法流程，挖掘其中可以被化归成和稀疏恢复相关的环节和步骤，可以形成不同的基于稀疏恢复的STAP技术。

从应用场景的角度，STAP技术应用的场景主要可以分为线性均匀阵列(ULA)和非ULA两大类，ULA中又可以分为正侧视ULA和非正侧视ULA，非 ULA阵列主要是指共型阵。根据不同的工程应用场景，STAP方法本身会有不同，相应的稀疏恢复STAP方法也会有区别。

表1列出了基于稀疏恢复的STAP方法这一问题的框架和结构，从信号处理结构和应用场景两个角度进行了划分，其中有些问题是已经有学者研究过并给出了系统的结论，在表1中用打钩的方式进行了标注，并且前文已经进行了综述；而空白处的相关问题尚未见到相关成果发表。

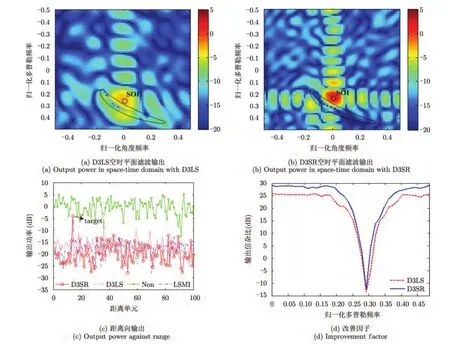
图11 非正侧视情形下D3LS与D3SR性能对比[29]Fig.11 Performance comparison between D3LS and D3SR in non side-looking case[29]

从表1可以看出，目前基于稀疏恢复的STAP方法的研究大部分都集中在正侧视 ULA阵列情形下，对于非正侧视 ULA阵列以及共型阵列的情形则只有较少的研究成果发表。在实际工程应用场景中，非正侧视 ULA阵列以及共型阵相关的问题有很高的应用价值，对于在这些场景下引入稀疏恢复之后的STAP方法的研究，具有重要意义。在非正侧视ULA以及共型阵情形下，杂波空时谱的稀疏性仍然满足，所以空时谱估计-滤波器结构的 SRSTAP的基本思想仍然适用，但是涉及到的其他一些具体问题仍有待进一步深入研究。在非正侧视阵列情形下，off-grid、阵列误差[30]，理想MMV，非理想MMV，降维/降秩等问题仍然存在。

表1 基于稀疏恢复的STAP技术的问题结构Tab.1 The structure of sparse recovery based STAP technology

现有的稀疏恢复STAP技术建立在杂波空时谱稀疏性的基础上，基于已有的常规信号观测结构。但从压缩感知与稀疏恢复的理论角度，完整的压缩感知和稀疏恢复过程应该包括这样两个环节：由经过设计的特定观测结构对稀疏信号进行压缩采样和对压缩观测信号进行稀疏恢复。所以，如果能够从压缩感知理论出发，设计特定的信号观测结构，保证压缩感知理论对观测矩阵的要求，并进一步在STAP处理环节采取相应的稀疏恢复方法，那么整个信号的观测和处理流程就会更加完善，处理性能也有望得到提升。

4 总结与展望

本文对基于稀疏恢复的STAP技术的已有研究成果进行了综述。首先介绍了基于空时谱稀疏性的谱估计-滤波器结构SR-STAP方法，然后对这一框架下的若干具体问题及最新研究成果进行了介绍，最后对其他潜在的研究方向进行了讨论。

压缩感知与稀疏恢复是信号处理领域近年来一个十分重要的研究方向。将其应用于STAP技术既是对自适应处理理论的扩充，在实际工程应用上也具有很高的价值。目前的研究现状表明，这一问题的研究尚处在起步阶段，在理论研究和工程应用上都有很多工作需要开展。希望本文能够给对这一研究方向感兴趣的读者提供参考和启发。

[1]Candès E J,Romberg J K,and Tao T.Stable signal recovery from incomplete and inaccurate measurements[J].Communications on Pure and Applied Mathematics,2006,59(8): 1207-1223.

[2]Candès E J and Tao T.Near-optimal signal recovery from random projections: universal encoding strategies?[J].IEEE Transactions on Information Theory,2006,52(12):5406-5425.

[3]Candès E and Romberg J.Encoding the lpball from limited measurements[C].IEEE Data Compression Conference,2006: 33-42.

[4]Candès E,Braun N,and Wakin M.Sparse signal and image recovery from compressive samples[C]. 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro,2007: 976-979.

[5]Candès E J and Wakin M B.An introduction to compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30.

[6]Donoho D L and Elad M.Optimally sparse representation in general (nonorthogonal) dictionaries via l1minimization[J].Proceedings of the National Academy of Sciences,2003,100(5): 2197-2202.

[7]Gorodnitsky I F and Rao B D.Sparse signal reconstruction from limited data using FOCUSS: a re-weighted minimum norm algorithm[J].IEEE Transactions on Signal Processing,1997,45(3): 600-616.

[8]Melvin W L.A stap overview[J].IEEE Aerospace and Electronic Systems Magazine,2004,19(1): 19-35.

[9]Sun Ke,Zhang Hao,Li Gang,et al..A novel STAP algorithm using sparse recovery technique[C].IEEE International Geoscience and Remote Sensing Symposium,2009: V-336-V-339.

[10]孙珂.非均匀杂波环境下基于稀疏恢复的STAP技术研究[D].[博士论文],清华大学,2011.Sun Ke.STAP technique using sparse recovery in heterogeneous clutter scenario[D].[Ph.D.dissertation],Tsinghua University,2011.

[11]Tang G,Bhaskar B N,Shah P,et al..Compressive sensing off the grid[C].IEEE Annual Allerton Conference on Communication,Control,and Computing (Allerton),2012:778-785.

[12]Zhu H,Leus G,and Giannakis G B.Sparsity-cognizant total least-squares for perturbed compressive sampling[J].IEEE Transactions on Signal Processing,2011,59(5):2002-2016.

[13]Chae D H,Sadeghi P,and Kennedy R A.Effects of basis-mismatch in compressive sampling of continuous sinusoidal signals[C].IEEE International Conference on Future Computer and Communication (ICFCC),2010,2:V2-739-V2-743.

[14]Bai Lin-da,Roy S,and Rangaswamy M.Compressive radar clutter subspace estimation using dictionary learning[C].IEEE Radar Conference (RADAR),2013,DOI:10.1109/RADAR.2013.6586160.

[15]Kim J M,Lee O K,and Ye J C.Compressive MUSIC:revisiting the link between compressive sensing and array signal processing[J].IEEE Transactions on Information Theory,2012,58(1): 278-301.

[16]Lee K,Bresler Y,and Junge M.Subspace methods for joint sparse recovery[J].IEEE Transactions on Information Theory,2012,58(6): 3613-3641.

[17]Ma Ze-qiang,Liu Yi-min,Meng Hua-dong,et al..Jointly sparse recovery of multiple snapshots in STAP[C].IEEE Radar Conference (RADAR),2013,DOI:10.1109/RADAR.2013.6586083.

[18]Zheng C,Li G,Zhang H,et al..An approach of DOA estimation using noise subspace weighted l1minimization[C].2011 IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP),2011: 2856-2859.

[19]Hersey R K,Melvin W L,McClellan J H,et al..Adaptive ground clutter suppression for conformal array radar systems[J].IET Radar,Sonar & Navigation,2009,3(4):357-372.

[20]Jaffer A G,Ho P T,and Himed B.Adaptive compensation for conformal array STAP by configuration parameter estimation[C].2006 IEEE Conference on Radar,2006,DOI:10.1109/RADAR.2006.1631883.

[21]Neyt X,Ries P,Verly J G,et al..Registration-based range-dependence compensation method for conformal array STAP[C].MIT Lincoln Laboratory Adaptive Sensor Array Processing Workshop,Lexington,MA,2005: 7-8.

[22]Lapierre F D,Ries P,and Verly J G.Foundation for mitigating range dependence in radar space-time adaptive processing[J].IET Radar,Sonar & Navigation,2009,3(1): 18-29.

[23]Ries P,Lesturgie M,Lapierre F D,et al..Knowledge-aided array calibration for registration-based range-dependence compensation in airborne STAP radar with conformal antenna arrays[C].IEEE Radar Conference,2007: 67-70.

[24]Sun Ke,Meng Hua-dong,Lapierre F D,et al..Registration-based compensation using sparse representation in conformal-array STAP[J]. Signal Processing,2011,91(10): 2268-2276.

[25]Sun Ke,Meng Hua-dong,Wang Xi-qin,et al..Conformalarray STAP using sparse representation[C].2011 IEEE Radar Conference (RADAR),2011: 576-579.

[26]Carlo J T,Sarkar T K,and Wicks M C.A least squares multiple constraint direct data domain approach for STAP[C].IEEE Radar Conference,2003: 431-438.

[27]Wang Xiao-qin and Han Chong-zhao.Direct data domain approach to space-time adaptive processing[J].Journal of Systems Engineering and Electronics,2006,17(1): 59-64.

[28]Sarkar T K,Wang H,Park S,et al..A deterministic leastsquares approach to space-time adaptive processing(STAP)[J].IEEE Transactions on Antennas and Propagation,2001,49(1): 91-103.

[29]Sun Ke,Meng Hua-dong,Wang Yong-liang,et al..Direct data domain STAP using sparse representation of clutter spectrum[J].Signal Processing,2011,91(9): 2222-2236.

[30]Sun K,Liu Y,Meng H,et al..Adaptive sparse representation for source localization with gain/phase errors[J].Sensors,2011,11(5): 4780-4793.