柔性基线抖动对机载干涉SAR性能影响分析

刘忠胜 汪丙南 向茂生 陈龙永

①(中国科学院电子学研究所微波成像技术重点实验室 北京 100190)

②(中国科学院大学 北京 100049)

1 引言

干涉合成孔径雷达(InSAR)集成了合成孔径雷达技术(SAR)和干涉技术，不但具有SAR全天时、全天候工作的优点，还可以获取地表高程信息，因此在军事和民用的各个领域得到了广泛应用[1－3]。干涉合成孔径雷达可通过重复轨迹飞行或双天线两种方式构建，重复轨迹干涉一般应用于星载模式，机载干涉SAR由于飞行轨迹难以精确控制，多数以双天线方式实现。与星载重轨干涉SAR相比，机载双天线干涉SAR具有作业效率高，同时不存在时间去相干，获取的数据相干性好，精度高等优点[4]。

在干涉SAR系统中，稳定的干涉基线是实现高精度测量的基础。根据干涉SAR系统高程灵敏度方程可知[5]，对于不同波段不同高程测量精度的要求，基线长度从亚米级、米级、几十米、甚至上百米。短波干涉SAR对植被穿透能力弱，只能获取数字地表模型(Digital Surface Model,DSM)，如果要获取植被丰富的森林地区的数字地形模型(Digital Terrain Model,DTM)，则需要系统工作于可以穿透植被到达地表的更低电磁波频段(如 P或 L波段)[6]。充分利用短波干涉和长波极化干涉各自的优势，可以实现森林地区的地形测绘和植被覆盖估计(例如美国JPL的GoeSAR[7,8])。与高频段干涉SAR系统相比，低频段干涉SAR系统需要更长的干涉基线。在机载双天线干涉SAR系统中，当干涉基线长度大于4 m时，基线呈现柔性结构。在雷达作业过程中，机载平台受航迹的调节和大气湍流等因素的影响，导致平台不仅偏离理想运动轨迹，而且会使柔性基线产生振动、扭曲等变形。因而在系统设计前分析基线抖动对干涉 SAR系统性能的影响具有重要的指导意义。

文献[9,10]分析了 SRTM 中基线抖动对其性能的影响，重点讨论了低频抖动对副天线图像和干涉相关性的影响。由于在星载平台中，不受大气湍流、重力等因素影响，卫星平台结构较为稳定，基线抖动频率可缩小到中低频率(SRTM 配备基于光学的基线测量系统测量频率仅为 10 Hz)。文献[11]建立了基线抖动造成的干涉SAR相位误差模型，针对一般斜距误差表达式，未给出干涉相位误差的定量化表达式，定性地分析了基线抖动对SAR干涉条纹的影响。

本文重点针对柔性基线机载干涉 SAR系统中基线抖动问题，从1次、2次和一般抖动3个方面详尽地分析了其对干涉 SAR图像聚焦和干涉性能的影响，并建立了相干性能分析的理论模型，最后通过仿真实验验证了理论分析的正确性。

2 柔性基线抖动下斜距误差模型

如图1所示，雷达主天线坐标系A1-xyz中，A1是主天线相位中心位置，x轴指向飞行速度方向，z轴垂直于地面向上，xyz构成右手系。A2为雷达副天线相位中心的位置，P为雷达波束照射带宽上任意目标点。由文献[9]可知，基线支撑臂俯仰和偏航引起副天线波束指向偏移，而沿支撑臂向的伸缩较小可以忽略，本文重点分析横滚向抖动引起的斜距误差。假设基线A1A2长度为B，与水平面倾角为α，主天线相对与目标P下视角θ，不存在基线抖动情况下，副天线斜距可表示为：

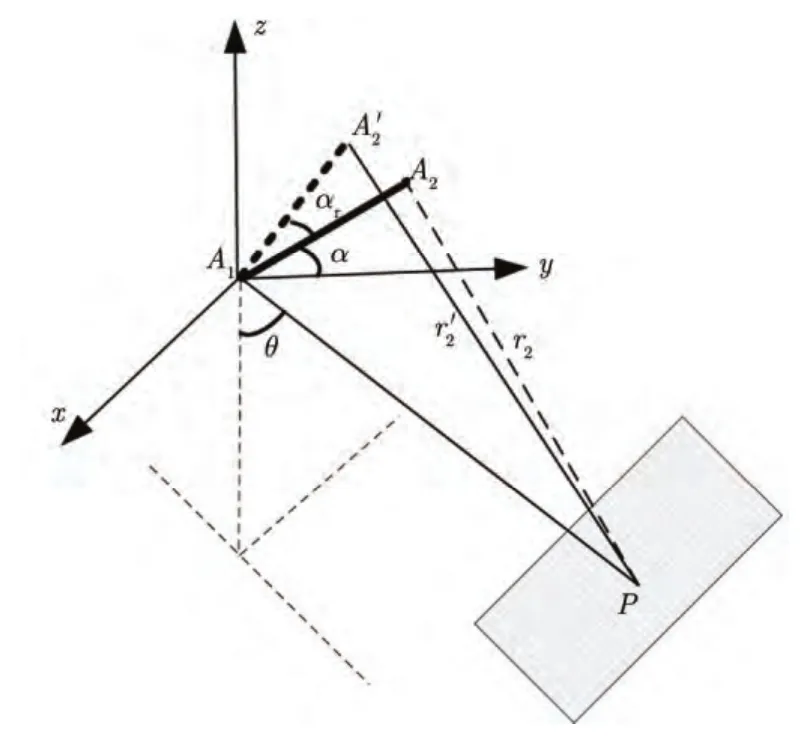
图1 柔性基线抖动模型Fig.1 Flexible baseline oscillating model

假设主天线位置不动，距离向存在基线抖动角αr时，副天线 A2移动到，由图1可知，副天线瞬时斜距变化为：

考虑到基线抖动幅度较小(大尺度的抖动可通过POS系统测量补偿)，有 sinαr≈αr,cosαr≈1，斜距误差可进一步简化为：

斜距误差对2维成像而言，影响图像方位向聚焦，从而更进一步降低干涉图像对相关性，最终影响数字高程精度。由式(3)可知，斜距误差与有效基线长度成正比，对于本文讨论长柔性基线而言，微弱的基线抖动均造成运动误差的产生。

在实际运行系统中，特别是机载双天线干涉SAR系统中，受平台机械结构、大气湍流等因素的影响，基线抖动是时变的，往往是多种振动频率的组合形式，为了简化分析过程，本文讨论单一频率下基线抖动对相干性能的影响。这种假设具有一定的普遍性，因为任意的抖动形式均可以表示成多个频点的正弦抖动和的形式。设距离抖动幅度和频率分别为Ar,fr，抖动角可表示为：

式中φ0是初始相位，将式(4)代入到式(3)中，得到：

考虑到2阶斜距误差导致方位调频率变化，是最为重要的一种斜距误差，将式(5)在方位中心时刻处泰勒级数2阶展开：

其中：Δr0=B cos(θ−α)Arsinφ0表示在方位中心时刻的斜距误差，斜距误差变化速度可表示为Vm=−2 π frB cos(θ−α)Arcos φ0。式(6)给出了柔性基线抖动导致的副天线2阶斜距误差模型，第3节将从低频线性1阶误差、2阶误差、高频误差3个方面建立复图像信号模型和相关系数模型，然后分析从低频抖动到高频抖动对干涉SAR性能的影响。

3 复图像和干涉性能分析模型

副天线接收 SAR原始回波信号经过距离压缩后2维时域表达式可表示为[12]：

其中发射信号波长λ，线性调频信号调频率为K，脉冲宽度为Tr,t是方位向慢时间，τ是距离快时间，wa(t)是方位向天线方向图调制，C1是无关的常数项，对式(7)进行方位向傅里叶变换，得到距离多普勒谱：

可采用驻定相位原理(POSP)对求取式(8)中的积分，将式(7)代入到式(8)中，并计算相位驻留点ts，式(8)可简化为：

相位驻留点的求取关系到斜距误差Δr的形式，下面将针对低频抖动和高频抖动误差，分别给出相应的副天线SAR图像信号模型。

3.1 1次斜距误差模型

当基线抖动频率较低时，即在方位处理时间内，可以对正弦函数进行线性化，1次斜距误差的表达式(6)可简化为：

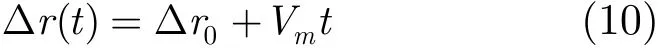
将式(10)代入到式(8)中，求取相位驻留点，计算方位向的时频关系 t=−(λ fa+2Vm)/(λ Ka)，从而得到存在斜距误差情况下方位压缩前距离多普勒谱：

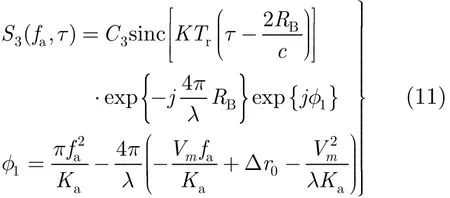
其中φ1是傅里叶变化后的相位项，Ka=2v2/(λ RB)为方位信号调频率，v是平台速度，RB是目标相对方位轨迹垂直斜距。φ1中第 1项为具有线性调频特性的频率方位调制项，第2项是由于线性斜距误差导致的相位误差项，由式(11)可知存在随方位频率线性变化的相位误差项。在频域内进行匹配滤波完成方位压缩，方位压缩后副天线2维时域复图像信号可表示为：

其中 Bd是方位向处理带宽，ψ1(t)是由于基线抖动造成的副天线图像带来的相位误差，Δt1=2Vm/λKa是线性斜距误差引起的图像方位向失配量。由式(12)可知：柔性基线线性抖动导致方位图像失配，不影响图像方位向聚焦，但对干涉SAR来说引起的相位误差将严重影响干涉系统性能。主副天线复图像相关系数可进一步计算[13]：

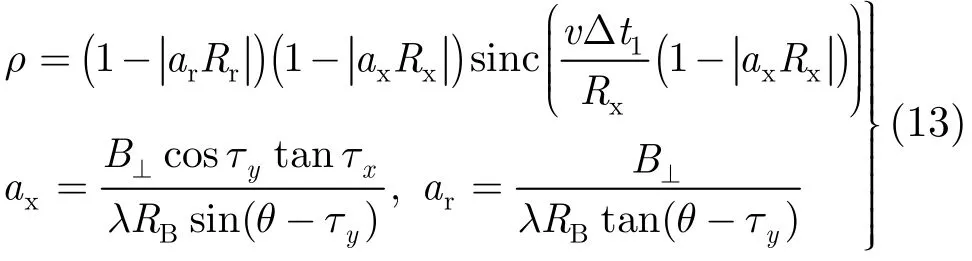
其中Rx,Rr分别是方位向和距离向分辨率，RB是场景中心斜距，τx,τy分别为地形沿x,y方向的坡度，B⊥是垂直有效基线长度。式(13)前面两项为空间基线导致的去相关，最后一项为基线抖动导致的相关性下降。当方位向定位偏移△t=0时，该项表达式值为1，那么式(13)退化为理想的相关系数表达式，进一步假设地形坡度为0，代入△t表达式值，该式可进一步简化为：

可见存在线性斜距误差情况下，干涉SAR系统相关性与基线抖动幅度和频率的乘积成反比例关系，基线抖动幅度越大、抖动频率越快，相关系数越小。图2给出了一种等相关系数变化曲线，由图2可知，双通道SAR图像为获得相等的相关性，抖动幅度和抖动频率约束形式近似为双曲线形式。例如当抖动频率为0.05 Hz时，可允许的抖动幅度可达0.25 m，即可保证0.95的相关系数。

3.2 2次斜距误差模型

当斜距误差可用2次函数来逼近时，参考式(6)我们将Δr(t)在方位中心时刻作2次泰勒展开：

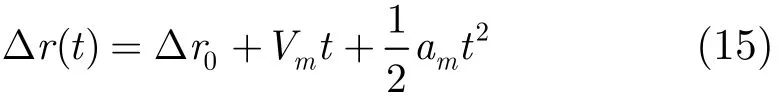
其中：am=−2Bcos(β−α)Ar(2πfr)2sin φ0，为求其距离压缩和距离徙动校正后的距离多普勒谱，方位多普勒域时频对应关系为t=−(λfa+2Vm)/(λ Ka+4am)，从而距离多普勒谱可表示成：

图2 线性抖动下相关系数曲线Fig.2 Correlation coefficient under linear oscillation

式中φ2的第 1项为具有线性调频性质的方位调制项，但多普勒调频率变化为，经过精确的距离徙动校正和方位压缩后，得到副天线图像信号表达式：

式(18)与式(14)相比，2次斜距误差情况下相关系数计算公式具备相似的规律(2次模型包含了线性误差)，然而由于方位调频率变化引起方位图像散焦，从而降低其相干性。

综上所述，基线抖动频率较低时对SAR成像和干涉性能的影响可以总结为：

(1) 基线抖动会造成方位分辨率下降，图像方位定位偏移，抖动幅度越大，频率越高，分辨率下降越多，图像定位偏移越大；

(2) 基线抖动对 SAR距离压缩的影响可以忽略，但会在距离向引入相位误差，影响干涉性能；

(3) 基线抖动造成的图像位置偏移会导致干涉图像对的配准误差，该误差会影响干涉相位和相干系数；抖动幅度和频率与干涉SAR系统相关性成反比例关系，基线抖动幅度越大、抖动频率越快，相关系数越小。

那天，李桂明的妻子回娘家了，就他一个人在家。他想，这是极好的机会。一早，他父亲嘱咐他早点回来，为帮他家做活的亲戚朋友做饭。

3.3 一般斜距误差模型

当基线抖动频率较快，在考察的方位时间内斜距误差包含2阶以上斜距误差分量，利用上述的方法不能够有效地解算出解析表达式，这里采用Jacobi-Anger展开相位误差项，将相位误差变换成一系列随慢时间以不同斜率线性变化的误差项和的形式：

其中Jn(⋅)是第1类Bessel函数，Δrm为基线抖动幅度最大值。其绝对值随着阶数n的增大而衰减，理论上任意幅度的运动误差均可以用有限阶展开项近似。幅度越小，衰减越快，则展开阶数越小。将式(19)代入 2维回波信号，经成像处理后复图像信号可表示为：

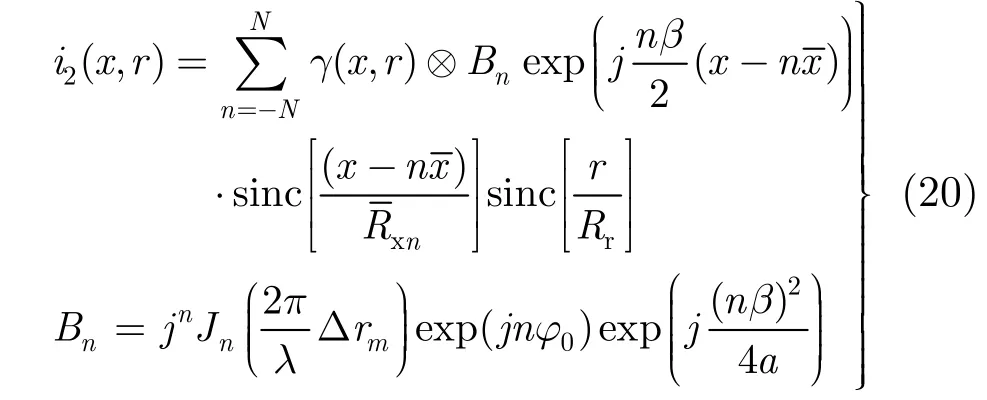
其中β=2π fr/v ,(T是SAR合成孔径时间)，(X是SAR合成孔径长度)，由式(20)可知，正弦形式的基线高频抖动造成复图像主瓣的两侧形成成对回波，总展开阶数，第n阶的成对回波偏移量为。1阶成对回波能量最强，距离主瓣最近，对成像的影响最大，这里着重分析1阶成对回波对成像的影响。图 3给出 1阶贝塞尔系数B1与基线抖动幅度最大值Δrm的关系曲线。由图3可知，当基线抖动幅度为5 cm时，1阶成对回波与主瓣能量只差5.6 dB，此时对成像和干涉的影响比较大，当基线抖动幅度为1 cm时，1阶成对回波与主回波能量差17.7 dB，如果基线抖动的测量结果能优于1 mm,1阶成对回波与主瓣已经相差了37.7 dB，此时成对回波对成像和干涉性能的影响可以忽略。由式(20)可得基线抖动对成像和干涉的影响包括：

(1) 成对回波偏移量与基线抖动频率成正比，与抖动幅度无关；当Tfr＜1时，1阶成对回波将对主瓣产生影响，将影响图像质量和相关性，这对应低频抖动的情形，不再赘述；

(2) 高频抖动引入了相位误差，相位误差的变化频率与基线抖动频率相关；抖动频率越大，相位误差变化越快；抖动幅度越大，引入的干涉相位误差越大；

(3) 当总展开阶数N＜1，即 fr＞ 2v/ la时，此时信号处理带宽内主回波两侧将不再出现成对回波，在振幅较小时，基线抖动对图像相关性的影响可以忽略，双通道图像相关性趋于一个定值；

(5) 基线抖动幅度主要是通过贝塞尔系数对相关性产生影响。如图4所示，曲线为贝塞尔系数幅度曲线随阶次和斜距误差幅度的变化曲线。当基线抖动幅度为1 cm时，1阶贝塞尔系数衰减为13%，2阶贝塞尔系数衰减为0.8%，能量几乎为0。抖动幅度越小，贝塞尔函数衰减得越快，因此当抖动幅度较小时，高阶成对回波的能量是非常小，对复图像对相干性的影响也很小。

4 仿真验证

为验证上述理论分析模型，通过在回波信号生成过程中添加基线抖动误差，最后经过成像处理和干涉处理，计算双通道SAR图像相关系数，从而验证柔性基线抖动参数变化对干涉性能的影响规律。实验参数如表1所示，采用L波段SAR，构建了16 m的柔性干涉基线，基线抖动幅度从0～300 mm，抖动频率从0～4 Hz范围内变化，分析在此变化范围内干涉SAR系统性能随参数变化曲线。

4.1 点目标仿真

图3 1阶衰减B1与Δrm的关系Fig.3 The relationship between the first-order attenuation B1and Δrm

图4 Bn随阶次及斜距误差幅度变化Fig.4 Bnchanging with the order and slant range error

表1 L波段雷达参数Tab.1 L-band radar parameters

图5给出了低频斜距误差对点目标方位成像的影响，斜距误差包括了1次项和2次项，斜距误差中2次项变化幅度为0.12 m,1次项变化幅度为0.08 m。从图5中点目标方位成像结果(经过了归一化处理)可知，一次项导致点目标定位偏移0.36 m,2次项导致方位图像分辨率从0.9 m下降为1.27 m，且峰值旁瓣比上升到−6 dB，成像质量大大降低。图6(a)是柔性基线抖动幅度为 1/8波长，抖动周期等于合成孔径时间时的方位脉冲响应函数(抖动频率0.11 Hz)，1阶成对回波叠加到主瓣单元，造成分辨率和旁瓣比恶化，这与低频抖动误差的分析结果一致。图 6(b)显示的是抖动频率增大到原来 4倍时(0.44 Hz)，1阶成对回波远离主瓣，主瓣成像指标基本不受影响。

4.2 面目标仿真

图5 2次斜距误差方位图像Fig.5 Azimuth image with quadratic slant-range error

图6 点目标方位图像Fig.6 Azimuth image of point target

图7 面目标干涉仿真结果Fig.7 Interferometric simulation result of scene

图8 不同基线抖动参数下的干涉条纹变化，8(a),8(b),8(c)为低频抖动仿真实验，8(d),8(e),8 (f)为高频抖动仿真实验Fig.8 Interferometric fringe changing with different oscillation parameters,8(a),8(b),8(c) for low frequency oscillation simulation experiment,8(d),8(e),8(f) for high frequency oscillation simulation experiment

图9 相关系数随基线抖动幅度和频率的变化Fig.9 Correlation coefficient changing with the amplitude and frequency of baseline oscillation

通过在干涉 SAR双通道原始回波信号模拟过程中添加各种形式的基线抖动[14,15]，并经过成像处理和干涉处理，得到干涉图像对的干涉条纹，并统计了双通道SAR图像相关系数。图7(a)为均匀目标成像结果，图7(b)为无误差情况下的干涉条纹。图8为不同基线抖动参数下的干涉条纹变化，图8(a)～图8(c)为低频抖动仿真实验结果，图8(d)～图8 (f)为高频抖动仿真实验结果。比较图8(a)和图8(b)，两者振动幅度A相同，频率F不同，图8(b)抖动频率大导致干涉条纹弯曲程度大；图8(a)和图8(c)中，两者振动频率相同，图 8(c)的振幅大干涉条纹弯曲程度大；图8(a)～图8(c)的仿真结果与3.1节和3.2节理论分析结果一致。对于基线高频抖动，由图8(d)和图 8(e)可知，两者振幅相同，抖动频率不同，干涉条纹弯曲快慢与基线抖动频率成正比；而由图8(d)和图 8(f)可知，两者抖动频率相同，幅度不同，干涉条纹弯曲程度与振幅成正比；这与 3.3节理论分析结果一致。图9表示干涉SAR系统相关性随基线抖动幅度和频率的变化曲线，图 9(a)是几种抖动频率下，相关系数随抖动幅度的变化曲线，首先看单条曲线，相关系数随抖动幅度增大而减小，且抖动幅度越大，相关系数的下降速度变快。例如抖动频率0.1 Hz曲线，振幅在100 mm以内时相关系数基本达到0.95，当振幅达到200 mm时，相关系数衰减到 0.85。再来比较不同频率的相关性数曲线，随着基线抖动频率的减小，相关系数逐步增大。当抖动幅度为100 mm时，抖动频率降到0.05 Hz时相关系数上升到0.973。这与3.1节低频抖动对相干系数理论分析一致。图9(b)为相关系数随抖动频率的变化规律，抖动频率从0变化到2 Hz过程中，相关系数随频率变化曲线首先下降，随后在1 Hz点附近后逐渐趋于一个定值。对于不同抖动幅度曲线相关系数最后的收敛值互不相同，抖动幅度越小，相关系数收敛值越大。当基线抖动周期与合成孔径时间(抖动频率约0.11 Hz时)相当时，成对回波相对主回波偏移量在一个分辨单元内，根据第3节分析，随着基线抖动频率和抖动幅度的增加，相关系数逐渐减小，因此曲线会在0.11 Hz点以前呈下降趋势。当基线抖动幅度较小时，随着抖动频率的进一步升高，成对回波逐渐远离主瓣，其与主回波的相关性逐渐减小，因而相干系数并不会继续下降，而是趋于一个稳定值。且收敛时的基线抖动幅度越大，相关系数收敛值越小。由图9(b)可知，20 mm振幅相关系数收敛于0.83，而振幅为10 mm时，相关系数收敛于 0.90。这说明当基线抖动幅度足够小时，无需进行运动误差补偿也可获得较高的干涉 SAR相关性能。但是基线抖动幅度较大时，图9(b)中，振幅为30 mm时，相关系数急剧下降，并不收敛于某一稳定值，因此对基线高频抖动，要严格控制振动幅度在一定范围内。图9(b)的仿真结果与高频振动理论分析基本一致。

5 结束语

柔性基线机载干涉SAR系统中，干涉基线的不稳定严重影响了干涉SAR系统性能。本文针对柔性基线机载干涉SAR系统中基线抖动问题，从SAR斜距误差模型出发，推导了 1次，2次和一般斜距误差下SAR复图像信号和双通道相关系数模型，并进一步理论分析了基线抖动对图像聚焦和干涉性能的影响。在理论分析的基础上，进行了仿真验证，采用点目标仿真验证了基线抖动对方位成像质量的影响，同时还开展了考虑基线抖动的干涉SAR面目标回波仿真，通过成像和干涉处理，仿真了不同参数下基线抖动对干涉条纹的影响，并统计各种基线抖动参数下的双通道图像的相关系数，得到相关系数随基线抖动幅度和基线抖动频率的变化曲线，验证了理论分析模型的正确性。

本文的研究结果对于柔性基线机载干涉 SAR系统设计、柔性基线估计和运动补偿具有重要的指导意义。

[1]Massonnet D and Rabaute T.Radar interferometry: limits and potential[J].IEEE Transactions on Geoscience and Remote Sensing,1993,31(2): 455-464.

[2]Richards M.A beginner’s guide to interferometric SAR concepts and signal processing[J].IEEE Aerospace and Electronic Systems Magazine,2007,22(9): 5-29.

[3]Dehghani M,Zoej V,Javad M,et al..InSAR monitoring of progressive land subsidence in neyshabour,northeast iran[J].Geophysical Journal International,2009,178(1): 47-56.

[4]Hensley S.Introduction to airborne SAR interferometry[C].EUSAR 2006,Tutorial.

[5]Sun Zhong-chang,Guo Hua-dong,Li Xin-wu,et al..Error analysis of DEM derived from airborne single-pass interferometric SAR data[C].Geoscience and Remote Sensing Symposium (IGARSS),Vancouver,Canada,2011:3405-3408.

[6]钟雪莲.机载重轨干涉SAR残余运动估计方法研究[D].[博士论文],中国科学院电子学研究所,2011: 3-4.Zhong Xue-lian.Residual motion estimation for airborne repeat-pass interferometric SAR[D].[Ph.D.dissertation],Institute of Electronics,Chinese Academy of Science,2011:3-4.

[7]Hensley S and Wheeler K.The geosar airborne mapping system[C].IEEE International Radar Conference,Alexandria,America,2000: 831-835.

[8]Reis J J,Williams M A,Hensley S,et al..Updating GeoSAR for full-pol interferometric capability[C].IEEE International Radar Conference,Pasadena,America,2009: 1-6.

[9]Franceschetti G,Iodice A,Maddaluno S,et al..Effect of antenna mast motion on X-SAR/SRTM performance[J].IEEE Transactions on Geoscience and Remote Sensing,2000,38(5): 2361-2372.

[10]王晓光,王治强,杨新,等.柔性基线抖动对星载双天线InSAR系统性能的影响分析[J].电子与信息学报,2011,33(5):1114-1118.Wang Xiao-guang,Wang Zhi-qiang,Yang Xin,et al..Analysis of spaceborne dual-antenna InSAR system characteristic under flexible baseline oscillation[J].Journal of Electronics & Information Technology,2011,33(5):1114-1118.

[11]汪丙南,张帆,向茂生.基线抖动对干涉SAR相位的影响[J].遥感学报,2010,14(6): 1171-1181.Wang Bing-nan,Zhang Fan,and Xiang Mao-sheng.Influence of baseline oscillations on SAR interferometric phase[J].Journal of Remote Sensing,2010,14(6): 1171-1181.

[12]Cumming I G and Wong F H.Digital Processing of Synthetic Aperture Radar Data[M].Boston,America,Artech House Publishers,2005,Chapter 3-Chapter 4.

[13]Rosen P A,Hensley S,Joughin I R,et al..Synthetic aperture radar interferometry[J].Proceedings of the IEEE,2000,88(3):333-382.

[14]唐晓青,向茂生,吴一戎.考虑基线抖动的双天线干涉SAR原始回波仿真[J].电子与信息学报,2009,31(8): 1856-1861.Tang Xiao-qing,Xiang Mao-sheng,and Wu Yi-rong.SAR raw signal simulation of dual-antenna InSAR accounting for baseline oscillations[J].Journal of Electronics & Information Technology,2009,31(8): 1856-1861.

[15]Khwaja A S,Ferro-Famil L,and Pottier E.Efficient stripmap SAR raw data generation taking into account sensor trajectory deviations[J].IEEE Geoscience and Remote Sensing Letters,2011,8(4): 794-798.