众筹融资模式中投资人协调博弈的实验研究

涂静，王鑫鑫

（武汉科技大学管理学院，湖北武汉430081）

众筹融资模式中投资人协调博弈的实验研究

涂静，王鑫鑫

（武汉科技大学管理学院，湖北武汉430081）

项目关键资金量和收益率的特征显著影响投资人选择合作的概率；资金量大的投资人更趋向于选择合作；投资人类型不对称时的合作概率显著高于对称时，众筹中领投制度能够减少协调失败的概率。

众筹融资模式；协调博弈；实验经济学

一、引言

相比传统融资方式，众筹融资模式有以下优点：（1）低门槛，众筹模式为小微创业项目提供了融资渠道，而个人投资者也可以通过对初创项目的投资分享项目成长的收益。（2）低信息成本，互联网为微小的资金参与创新项目提供可能，使得项目方与投资方得以高效匹配。（3）检验市场反应，创新是否受到大众的认可在融资启动阶段就可以进行检验。2012年美国政府通过《创业企业融资法案》，创业企业的众筹融资模式合法化，众筹模式参与者的权益受到法律保障。但众筹融资在我国还存在法律监管上的空白，如何根据我国国情，借鉴国外监管机制为众筹提供合法保障，是从监管立法的角度关注众筹融资问题[1]。

但是在有效监管下，与风险投资等专业投资机构相比，众筹融资模式也存在效率问题，这正是本文关注的问题。风险投资机构一旦确定投资，很少会在中途放弃项目，即使是在创业公司处于困境的时候，也会为它们制订计划并耐心地帮助它们解决困难。众筹能帮助初创项目快速筹到用于产品研发和生产的资金，但不能保证今后的资金链完整。当项目的成长状况不明朗时，众筹项目中个人投资者之间可能会出现协调失败。协调失败的原因在于：（1）众筹中的投资者是非专业对风险的容忍度很低，当不确定性出现时更趋于选择风险占优策略；（2）众筹中个人投资者是分散的，彼此之间不知道对方的策略，也没有有效的机制约束他人的策略。协调失败导致参与者在观察到项目的不确定性信息时，纷纷从项目中撤资，最终项目因为资金链不完整而失败。创业项目的发起人大费周折之后才意识到最容易得到的钱，到最后其实是最难维系的钱。

此时如果有足够的资金支持，项目可以避免失败，投资人也可以获得大于本金的收益，但支持项目继续的关键资金量是否能够达到取决于参与者的个人决策。每个参与者都知道最好的决策是跟随其他参与者的决策：如果其他的参与者都愿意继续，则自己也应该选择继续；如果其他的参与者都选择撤资，则自己的最优选择也是撤资。但当参与者不能获得确定的信息时，无法知道哪一个均衡会实现，这就是众筹模式中的协调博弈。

二、相关文献综述

Cooper和John(1988)指出主体之间如果存在着战略互补，即一个参与者的合作策略会给其他参与者带来正外部性时，那么博弈通常会出现多个帕累托排序的均衡，这一问题被称为协调博弈(coordination game)，当参与者在多个均衡中选择了一个帕累托次优的均衡，协调失败就发生了。Harsayi和Selten(1988)在经典的猎鹿博弈中定义了风险占优均衡和支付占优均衡，他们认为如果风险和支付一致时，博弈将收敛于唯一的效率均衡，但协调博弈中的支付与风险出现不一致性时，协调问题中的难点出现了[2]。Bravo和Siciliani(2007)认为，在参与者决策互补性的情况下，独立做出他们的决策时，很难推测其他人的决策，决策问题成为了一个两难的协调问题。李艳梅等(2007)指出协调博弈的多重均衡导致了制度的多样性,于是不同制度间的效率差异产生了制度变迁的压力,但是制度变迁能否实现还取决于与制度所对应的均衡是否具有随机稳定性[3]。博弈论仍无法找到强有力的方法来解决哪一个均衡会真正出现。从预测能力来看，博弈论在多重均衡问题上并不完善，其结果是博弈论学者已经成为实验经济学最经久不衰的使用者。实验经济学是协调博弈均衡选择研究中最重要的方法，通过对参与者真实行为的研究，探讨影响协调博弈中均衡选择的因素。Van Huyck等(1990)的实验研究表明，参与者之间协调成功，收敛于Pareto最优均衡并不是一个确定的结果。Croson和Marks(2000)在公共品提供博弈中提出了供给阈值的概念，超过阈值后外部性效应才出现，外部性用总收益与阈值之比来描述。Devetag(2003)实验借鉴了公共品实验中的阈值，提出了关键量的概念，用收益率来描述外部性，设计实验考虑了关键量和支付收益因素，认为在完全的信息反馈能够改善协调的效率。Van Huyck等(2007)设计了一个多轮实验，发现实验对象的策略随时间推移而不断收敛，最终达到支付占优，说明学习对克服协调失败具有改善作用。蒲勇健(2005)研究当协调博弈的参与者观察到收益信息是异质的不完全信息时，做出是否合作的决策，得到影响参与人的收益阈值。Heinemann等(2009)研究了协调博弈中关键量的影响，参与者面对一个支付占优和一个风险占优略的选择，随着关键量要求的增加，选择风险占优的人数也在增加。Mak和Zwick(2010)研究了战略互补的参与者的投资决策及其协调问题，设计了一个多轮博弈实验，不仅考虑投资者数量，还加入了投资关键量的影响，研究两个因素共同对参与者投资行为的影响，发现第一轮的结果如果达到的投资关键量，那么博弈会收敛到一个帕累托最优均衡。Cherry (2013)用实验比较了发生在市场中和公益中的协调博弈，发现无论参与者之间存在正外部性还是负外部性，公益中的协调行为都显著高于市场中，更容易收敛于支付占优的均衡，尤其是在公益和正外部性结合的情况下。

在已有协调博弈的影响因素的研究中，存在参与人是同质的基本假设，在此基础上研究信息反馈、参与者人数和关键量等因素对其行为的影响，本文引入了异质的参与人。希望通过对比同质和异质的投资者，观察投资者类型是否对协调行为产生影响。而且区别于Croson和Marks(2000)中外部性的测量。众筹项目与公共品不同，收益率与关键量是相互独立的，我们理论模型中定义了独立的收益率与关键量。本文研究的目的是探讨以下三类因素对众筹模式中投资人协调行为的影响：项目成长要求的关键资金量、项目的收益率以及项目投资者的类型，进而分析投资人之间协调失败的因素。

三、实验的博弈模型

初创项目的投资需要一个较长的过程。在项目的中间阶段，投资人可以观察到项目的成长情况P (P=failure,uncertain,success)，根据观察到的P选择撤资(S=0)还是继续(S=1)。我们以简化的两人投资的博弈矩阵，描叙投资人策略及其均衡问题，如图1所示。当观察到P=failure时，无论投资人是否撤资，项目一定失败，博弈只有一个均衡(0，0），投资人的最优策略是S=0，获得支付r。当观察到P=success时，无论投资人是否撤资，项目一定成功，博弈只有一个均衡(1,1)，投资人的最优策略是S=1，获得支付R，R>r。当观察到P=uncertain时，项目是否能成功并不确定，项目的成功取决于众投资人是否选择继续支持项目的成长，此时博弈有两个均衡：(0，0）和(1,1）。(0,0)是一个风险占优均衡，无论其他人的选择，自己选择S=0总能够获得支付r，此时项目失败。(1,1)是一个支付占优均衡，如果其他人选择S= 1，自己选择S=1可以获得R的支付，此时项目成功。但(1,1)均衡中风险和支付不一致，如果其他人选择S=0，自己却选择了S=1，支付为0，项目失败。

图1 投资人的博弈矩阵

P=uncertain时产生的多个均衡问题正是本文研究的投资人协调博弈模型的背景。模型假设存在一个项目，项目持续三个时期(T=0，1，2)和n个投资人。T=0是项目的融资期，T=1是项目的中间期，T=2是项目的结束期。投资人i在T=0时期投入mi单位的资金。T=1时期，投资人观察到P=uncertain的信息：如果选择S=0，可以获得T=0时投入的本金，退出项目；如果选择S=1，进入T=2时期。项目在T=2时期的是否成功取决于是否有足够的资金维持项目的成长，项目维持所需最低资金量为关键量k。如果项目内留存的总资金量超过了k，项目成功，每位选择继续的投资人都可以获得不低于本金的净收益；如果项目内留存的总资金量小于k，项目失败，每位选择继续的投资人的支付为0。T=2时期，选择继续的投资人的支付实现，投资人的支付取决于自己在T=0时期的投入，项目内的留存资金量，以及项目的收益率λ。综上，投资人i的支付函数πi定义为

四、实验设计

实验在学校经济学实验室进行，从学校高年级的本科生中我们招募72名实验对象，实验对象以前均没有参加过类似实验。Fehr(2002)证实了其可行性，认为这一实验对象不会受思维定势的局限，比较容易实现与实验主题的行动一致性。而且实验所研究的背景，对实验对象的要求正是对互联网金融有接受度的非专业个人投资者。72名实验对象被随机分配到12个实验组。每个组由6个实验对象组成。实验者和实验对象都不知道实验对象的分组信息，以减少偏见和无意识地暗示对实验结果的影响。

根据研究目标，实验设计中的自变量为项目的关键资金量，项目的收益率以及项目投资者的类型，为此采取2×2×2实验对象内设计来描述这3个维度的处理变量。第一个维度用来描述项目的关键资金量，分为两级处理水平：k=40为低关键量(LC)，k= 80为高关键量(HC)。第二个维度用来描述项目的收益率，分为两级处理水平，λ=2.5为低收益率(LE)，λ=3.5为高收益率(HE)。第三个维度用来描述项目的投资者类型，分为两级处理水平：对称处理(SYM)中，投资者的资金投入是相同的，6个实验对象在T=0期投入的资金为(20,20,20,20,20,20)；不对称处理(ASYM)中，投资者的资金投入是不同的，6个实验对象在T=0期投入的资金为(10,10,10,30, 30,30)。但资金总量在对称和不对称投资者实验组中都同为120，表示项目的资金量需求相同。

在T=1时期，实验对象观察到项目成长的不确定信息，实验对象的战略空间为(1,0)，1表示对项目继续融资，0表示从项目中撤资，实验对象同时做出是否投资的决策。实验对象决策的依据为支付函数，如式（1）所示。由于博弈中，支付不仅取决自己的策略，也取决其他参与人的策略，我们也给实验对象提供了由支付函数计算得出的二维支付表作为决策的参考，通过支付表，实验对象可以得到在给定实验组其他参与者的决策下，选择“1-choice”的支付。

每个实验对象发放了一张答卷，要求给出12个决策环境下的选择，如表1的处理水平列所示。其中4个为参与者类型为对称处理下的决策，8个为参与者类型为非对称处理下的决策。每个实验对象分别赋予三种角色，在不对称的处理中的小额投资人(m=10)和大额投资人(m=30)，在对称处理中的中额投资人(m=20)。

实验经济学的实验对象是真实的人，价值诱导是激发实验对象做出真实决策的手段。价值诱导理论(Smith,1976)的观点是：使用的报酬媒介使得实验对象能表现出实验者想要的特质，且参与者本身固有的性质大部分变得毫不相关。在参与者理解实验指导书的前提下，设定现金报酬与实验对象在实验中支付之间的比例关系，这样实验对象收到的报酬由他的行为（以及其他参与者的行为）来决定，行为和报酬之间的关系实现了预想的规则。我们设定实验现金与人民币的兑换比率为1∶1。实验结束，收回72份答卷。从12个决策中，抽取2个决策，每个实验对象的支付为其这2次决策所获支付的平均数。实验时间为35分钟，实验对象的平均支付为27元。现金报酬采取匿名领取，满足其占优性。

五、实验结果和分析

我们给出了实验12个处理水平的参与者的决策结果统计，如表1。本文中将参与者选择1-choice定义为合作行为，即个人投资者都选择继续，合作支持项目的成长，这也是协调博弈的支付占优策略。实验数据的统计结果显示，最终均衡偏离了支付占优，与以往协调博弈的实验研究相似，Pareto最优均衡不是一个确定的结果。

首先我们得到项目的关键资金量和项目的收益率是如何影响参与者的合作行为。表2给出了logit regression的结果。其中，独立变量是选择1-choice的概率，λ和k/120为解释变量。k/120描述关键量资金占项目初始融资量的比例。回归的结果显示在无论项目参与者类型是ASYM还是SYM，项目的关键资金量和收益率对参与者的合作行为有着显著的影响，所有的系数小于1‰，Hosmer-Lemeshow检验的p值显著大于5%的显著水平。Logit回归模型的系数显示：参与者的选择1-choice的概率随着收益率的增加而增加，随着关键资金量的增加而减少。特别是在LE-HC处理中，选择0-choice的概率与0.95没有差异，而在HE-LC处理中，选择1-choice的概率与0.99没有差异(Binomial检验，p=0.077和p 0.633)。本文中我们将LE-HC定义为“0-equilibrium”条件和HE-LC为“1-equilibrium”条件，即投资人面对具备LE-HC特征的项目会收敛于“0-equilibrium”，而面对HE-LC特征的项目会收敛于“1-equilibrium”。

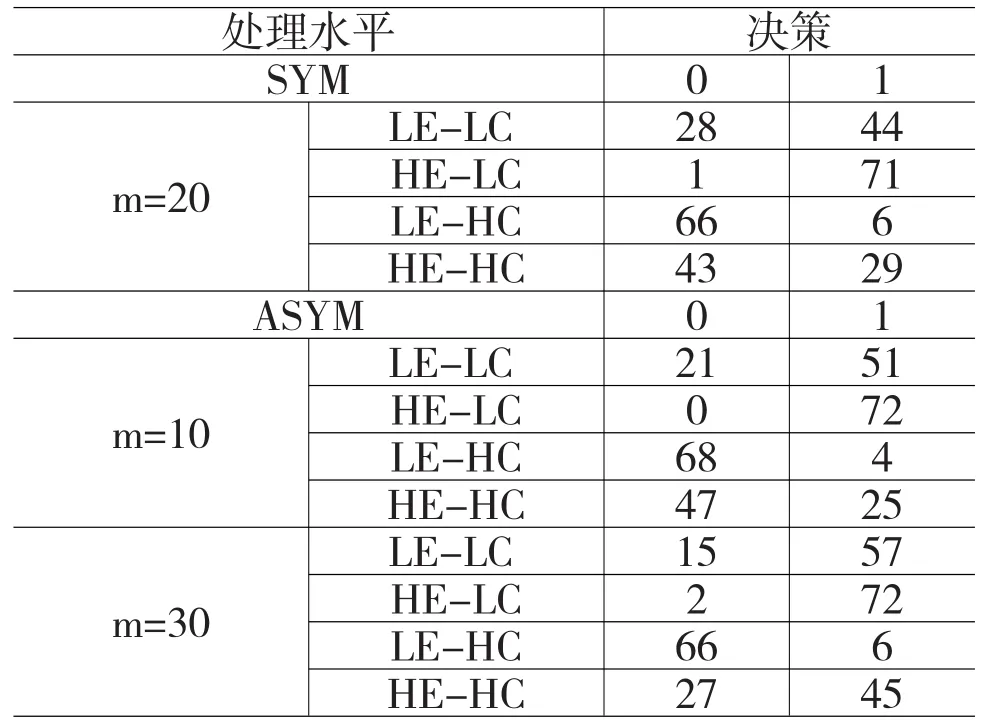
表1 参与者的决策结果统计

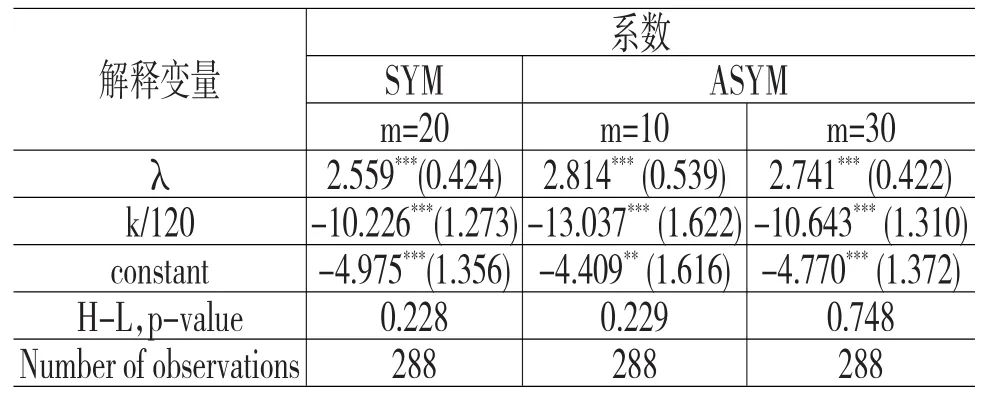
表2 选择1-choice概率的Logit回归解释

结论1：无论项目参与者类型是否对称，参与人选择继续合作的概率随着项目收益率的增加而增加，随着项目成长所需资金量的增加而减少。下面，我们得到当项目参与者类型不同的情况下，参与者的合作行为是否有所差异。将ASYM和SYM中的合作行为进行对比，其中SYM中的合作行为作为比较的基准。对LE-LC，HE-LC，LE-HC和HE-HC四种收益率和关键资金量的组合处理水平下，检验选择1-choice的频数是否与参与者的类型有关，采取Fisher精确检验。表3分别给出了四种组合处理水平下：m=10与m=20，m=30与m=20类型投资人行为是否存在显著差异的Fisher精确检验P值。

表3 对称和不对称参与者的合作行为比较

结果显示，在LE-HC和HE-LC处理水平下，即“0-equilibrium”条件和“1-equilibrium”条件下，ASYM中m=10的参与者和SYM中m=20的参与者在合作行为没有显著差异(p=0.5 and p=0.372)，ASYM中m=30的参与者和SYM中m=20的参与者在合作行为没有显著差异的m=10(p=0.5 and p=0.618)。

结论2：在LE-HC和HE-LC下，项目参与者类型对策略的选择没有显著影响，无论是大额投资者、中额投资者和小额投资者，在LE-HC下策略收敛于不合作的“0-equilibrium”，在HE-LC下策略收敛于合作的“1-equilibrium”。在LE-LC和HE-HC处理水平下，m=20的参与者与m=30的参与者合作行为存在显著差异(p=0.014和0.006)，资金量大的投资人更趋于选择合作策略，但m=20的参与者与m=10下的参与者，资金量存在差异，合作行为却没有差异(p=0.146和p=0.303)。

结论3：对于“0-equilibrium”和“1-equilibrium”之间特征的项目，资金量大的投资人更趋于选择合作策略，而且ASYM处理中的小额投资人因为有大额投资人的参与，也更趋于合作策略。与SYM处理下的中额投资人相比，ASYM下的小额投资人，即使资金量水平低，选择合作行为没有差异。因此，ASYM下的合作行为大于SYM。

五、结论

众筹融资中协调失败的概率随着项目收益率的增加而减少，随着项目关键量资金量的增加而增加，与投资者类型无关。因此，低收益率高关键量特征的项目，投资人策略收敛于撤资均衡，不适用于众筹融资模式；高收益率低关键量特征的项目，投资人策略收敛于继续融资均衡，适合众筹融资模式。

在这两个纯策略均衡之间特征的项目，资金量大的投资者更愿意选择继续融资。而且项目投资人类型不对称时，众筹更容易协调成功，有大额投资人参与的项目，小额投资人也更愿意选择继续融资。众筹融资中对投资者并没有设定准入门槛，但鼓励大额投资者领投后，个人投资者才可以进行跟投的融资制度对项目的协调成功是有效的，即使在大额投资者缺乏机构专业性情况下。

[1]胡吉祥，吴颖萌.众筹融资的发展及监管[J].证券市场导报，2013，（12）：60-65.

[2]Harsanyi J C,Selten R.A General Theory of Equilibrium in Games[M].MIT Press,Cambridge,1998.

[3]李艳梅，杨涛，荣朝和.协调型制度的进化博弈分析[J].管理工程学报，2007，21（2）：134-137.

（责任编辑：王淑云）

1003-4625（2014）10-0059-04中图分类号：F830.39文献标志码：A

2014-08-14

本文为2014年湖北省科技厅软科学研究专项资助项目(2014BDF107)“创新项目众筹融资中的协调失败与政策建议”的部分成果。

涂静（1975-），女，博士，副教授，研究方向：互联网金融，博弈论；王鑫鑫（1980-），男，博士，副教授，研究方向：商业模式创新。