电网电压三相不平衡时CVUF相角因素对异步电机运行性能影响
2014-09-28刘晓芳张元星赵海森王翔宇
刘晓芳,张元星,赵海森,王翔宇,韩 志,王 鹤
(1.华北电力大学 新能源电力系统国家重点实验室,北京 102206;2.中国电力科学研究院,北京 100192)
0 引言
电压不平衡是电力系统中一种普遍的电能质量偏差现象,包含幅值与相角不平衡因素,且主要由电网中三相负荷分布不均造成。异步电机运行在此状态下会产生损耗增加、温升过高、寿命缩短及输出转矩减小等不良影响[1-3]。为了探索电压不平衡条件下异步电机安全运行及节能控制策略,有必要针对电压不平衡时相角因素对异步电机定子三相电流、各项损耗及转矩性能的影响进行研究。
已有大量文献对三相电压不平衡对异步电机运行性能及损耗的影响开展了相关研究。文献[4]指出复数电压不平衡度 CVUF(Complex Voltage Unbalance Factor)同时包含幅值和相角不平衡因素,分析了CVUF相角对异步电机运行性能的影响,最终提出在分析异步电机不平衡运行问题时必须考虑CVUF相角对其的影响;文献[5]建立了三相感应电动机瞬态模型,使用四阶龙格库塔方法计算了不同CVUF时感应电动机的起动过程,研究了CVUF与最大转矩、起动时间、稳态三相电流不平衡因数、转速及其波动、转矩波动的关系;文献[6]指出美国电气制造商协会(NEMA)与国际电工委员会(IEC)对电压不平衡度(VUF)的定义均不是最精确的,基于这些定义对电机运行性能的分析也是不准确的,因此有必要制定一个更精确的VUF定义;文献[7]对电压不平衡条件下异步电机的损耗、温升、噪声、振动、转矩脉动、转差率、轴电压、轴电流和加速转矩进行了分析,并指出电压不平衡导致转子损耗增加,且定子电流不平衡会引起定子各相绕组温度分布不均,同时造成加速转矩减小及2倍频的转矩脉动;文献[8]使用对称分量法及MATLAB仿真得到如下结论:综合IEC中VUF定义与电压不平衡情况可以精确地评估电压不平衡对异步电机总铜耗、输入功率、功率因数及总输出转矩的影响程度,但同时也要考虑CVUF相角对三相绕组最大电流及降额因数的影响,并定义了一种区分电压不平衡状况的过欠系数,它有助于对电压不平衡条件下异步电机的运行性能进行更为准确的评估。综上,已有研究在参考的VUF评估标准上存在一定分歧[6],或并没有考虑电机实际运行时三相绕组电压矢量和为0[9],或没有同时考虑VUF与正序电压(或平均电压)[5],且大部分文献中所采用的传统磁路分析方法与等值电路理论由于无法计及饱和及谐波等因素而存在较大误差。
针对以上问题,本文利用对称分量法计算并分别表示出电机绕组三相电压幅值、两相电压相位与CVUF幅值及相角的关系,并针对一台5.5kW Y132S-4异步电机,建立了基于时步有限元的损耗计算模型,分析了CVUF相角对定子三相电流、各项损耗及转矩性能的影响。需要说明的是,由于电压不平衡情况较为复杂,包括CVUF幅值kv(负序电压和正序电压幅值之比)、CVUF相角θv、正序电压及负载率4个影响因素,且经试验测得上述电机在kv=0.05及75%负载下运行时最大单相电流已超过额定电流,故文中仅针对 75%负载、kv≤0.05[10]及正序电压为 380 V的情况开展研究。
1 CVUF定义及三相绕组电压幅值、相位与CVUF间的关系
1.1 CVUF定义
国内外通常采用以下VUF计算方法,即线电压不平衡度(LVUF)、相电压不平衡度(PVUF)、VUF 和CVUF。 文中采用 IEC 精确定义[11],如式(1)所示。
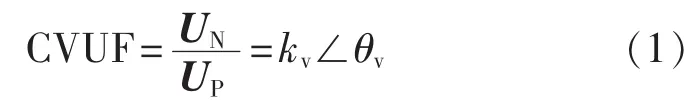
1.2 三相绕组电压幅值、相位与CVUF间的关系
1.2.1 三相绕组电压幅值与CVUF间的关系
在给定CVUF及正序电压UP的情况下,可以根据对称分量法以及基尔霍夫电压定律反求出该电压不平衡状态时的三相绕组电压。例如,在kv=0.05、-180°≤θv≤180°、350 V≤≤410 V条件下,三相绕组电压 Uab、Ubc、Uca幅值的三维关系如图1所示,其中三维图形表面上的经线、纬线分别表示CVUF相角θv和正序电压幅值,图中已将为350 V、380 V、410V的3条纬线标出。从图中可以看出:kv=0.05时所对应的三相不平衡电压组合情况有很多种,因此使用其中某一组电压去衡量该CVUF幅值下电机的运行性能会引起较大的误差。
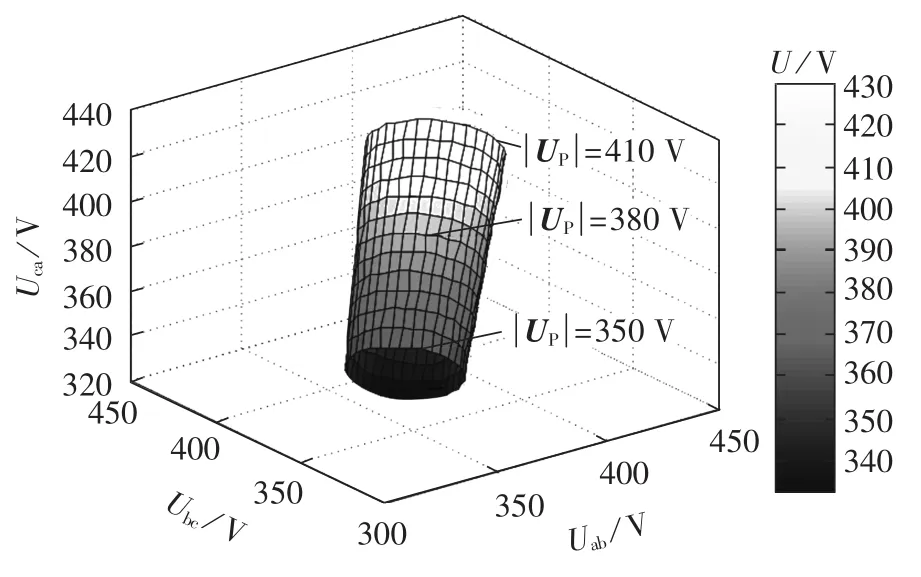
图1 kv=0.05 且-180°≤θv≤180°时三相绕组电压幅值Fig.1 Three-phase winding voltage amplitudes when kv=0.05 and -180°≤θv≤180°
1.2.2 三相绕组电压相位与CVUF间的关系
假设Uab相位始终为参考相位,且值为0°,可将电压不平衡时Ubc相位θbc与 kv、θv关系表示成图 2所示。 图 2(a)为 θv相同时 θbc随 kv的变化规律,仅以4组θv进行说明,可见:θbc随kv呈线性规律变化,且 θv=-100°时,θbc随 kv的变化率较大;而在 θv=-30°时,θbc随 kv的变化率近似为 0。 图 2(b)为 kv相同时θbc随 θv的变化规律,可以看出:θbc随 θv呈正弦规律变化,且变化幅度随kv的增大而增大。同理可得Uca相位θca随kv、θv的变化规律。 此外,在保持kv相同前提下,对正序电压在350~410 V时的两相电压相位进行计算时,发现不同正序电压下每一θv所对应的两相电压相位均相等。因此可认为:任何给定kv条件下,所求两相电压相位与正序电压大小均无关。
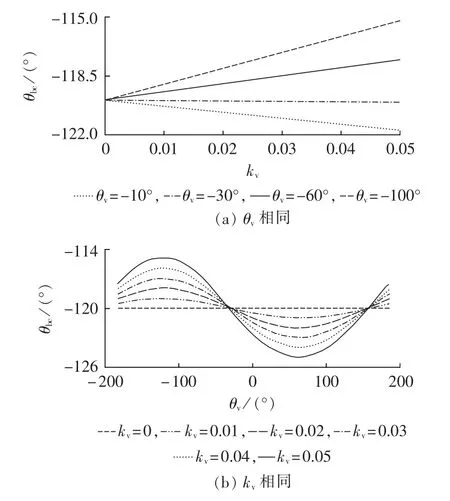
图2 恒定 θv(kv)下 θbc随 kv(θv)变化规律Fig.2 Relationship between θbcand kv(θv)when θv(kv) is constant
综上,结合图1与图2,可得任意kv、θv及正序电压条件下的三相绕组电压幅值与相位,如CVUF=0.05∠50°且正序电压为 380 V 时,Uab=392.5∠0°V,Ubc=386.9∠-124.8°V,Uca=361.3∠-241.6°V,且每个CVUF对应多种三相不平衡电压组合,按照正序电压大小可将其分为欠电压不平衡与过电压不平衡。
2 时步有限元法
2.1 时步有限元模型建立
本文以一台5.5 kW Y132S-4异步电机为例,其基本参数如表 1 所示,绕组为△接法。表中,U′N、PN、IN、nN分别为电机额定电压、额定功率、额定电流和额定转速;p为电机极对数。基于表1参数,建立了如图3所示的有限元模型,其中左半部分为电机定转子基本结构,右半部分为有限元剖分网格图。
2.2 时步有限元损耗计算方法
与传统计算方法相比,本文采用的时步有限元损耗计算模型可以在计及饱和及谐波等因素前提下,对电机内部任意单元的磁通密度和电流密度进行计算,在损耗计算方面具有明显优势,其中定子铜耗、转子铜耗以及铁耗均采用文献[13]中的计算方法;且由于本文所分析电机为斜槽转子,电机内部磁场沿轴向分布不同,故利用文献[14]中的多截面场-路耦合时步有限元法进行计算。

表1 5.5 kW Y132S-4电机参数及尺寸Tab.1 Parameters and size of 5.5 kW Y132S-4 motor
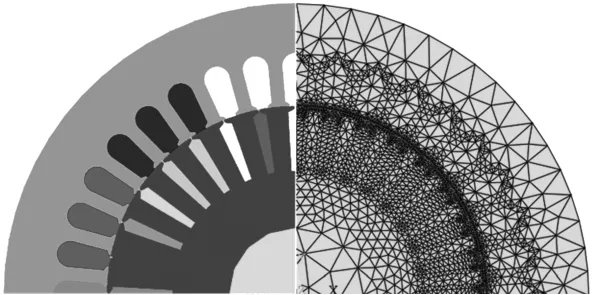
图3 5.5 kW异步电机有限元结构及剖分图Fig.3 FEM structure and subdivisions of 5.5 kW motor
3 CVUF相角对定子电流的影响
对异步电机定子绕组施加 kv=0.05、-180°≤θv≤180°条件下的三相不平衡电压,经时步有限元计算得到每组电压下定子三相电流随θv的变化规律如图4所示。从图4中可以看出:电压不平衡时,三相电流IA、IB、IC有效值随θv均呈正弦变化规律,且三者出现最大值时的θv互差120°。经计算验证,kv分别取值 0.01、0.02、0.03、0.04 条件下,三相电流变化规律与此相同,故不再赘述。
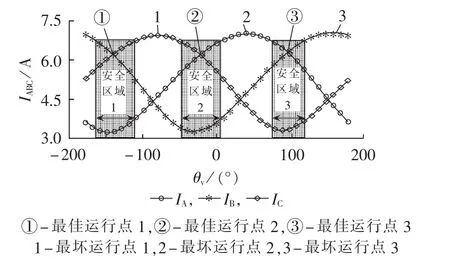
图4 kv=0.05且75%负载时定子三相电流与θv的关系曲线Fig.4 Curves of three-phase stator current vs.θvwhen kvis 0.05 and load is 75%
受温升限制,电机长期运行时绕组电流应不超过额定电流,而电压不平衡会引起绕组电流出现不平衡,为了确保不平衡电压下电机安全稳定运行,就需要限制单相最大电流不超过额定电流,据此可确定电机安全运行区域如图4中所示。图中,当某相定子电流出现最大值时的θv为电机最坏运行点,任意两相定子电流相同且不超过额定电流时的θv为电机最佳运行点,可以看出在 -180°≤θv≤180°范围内,有3个安全运行区域且每个安全区域内存在1个最佳运行点,而在安全区域外有3个最坏运行点。图4中所示kv=0.05且电机带75%负载时,最坏与最佳运行点时的 θv分别为:-80°、40°、160°与- 140°、-20°、100°。
需特殊说明的是,本文仅针对系统中允许的较低CVUF幅值进行研究,为处理方便,对电机正、负序等效电路作简化处理,由电机学理论分析可知:电机最坏、最佳运行点时的 θv分别由式(2)、(3)决定。
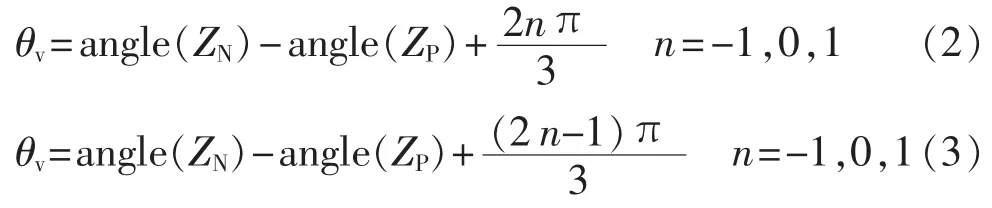
其中,ZP、ZN分别为从异步电机定子绕组端看进去的正、负序等效阻抗;angle为阻抗角的运算命令,如Z=R+jX,则 angle(Z)=arctan(X/R)。 ZP、ZN可分别由图 5(a)、(b)所示的正、负序等效电路[15]计算得到,结果分别如式(4)、(5)所示。
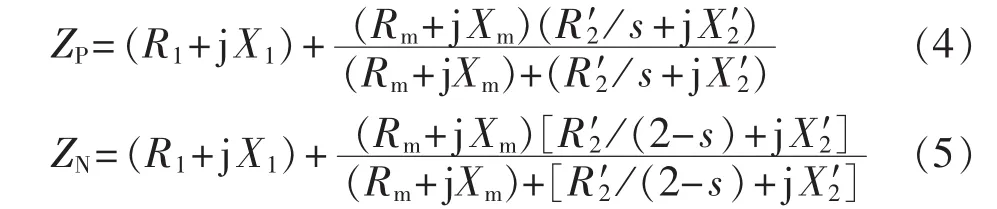
其中,R1、X1、R′2、X′2、Rm、Xm、s分别为定子电阻、定子电抗、转子电阻、转子电抗、激磁电阻、激磁电抗和转差率。

图5 异步电机正、负序等效电路Fig.5 Positive and negative sequence equivalent circuits of asynchronous motor
经空载与堵转试验可知,文中所分析5.5kW异步电机的正、负序等效阻抗 ZP、ZN分别为(47.2+j30.5)Ω、(3.5+j11.9)Ω,因此 angle(ZN)-angle(ZP)=40.5°,为图4中的最坏运行点,故计算结果与理论分析是一致的。该最坏运行状态时θv的含义为:此时A相的正、负序电流分量接近同相致使该相电流达到最大值。
综上,电压不平衡时,应根据电机参数求得最佳、最坏运行点,尽量使其工作在最佳运行点,以使在该CVUF幅值下电机带载能力下降程度最少。另外,在设计电机负序电流保护电路时,若只考虑kv影响时,则可能会由于电机运行在最坏运行点且单相最大电流已超额定电流,保护电路未发出动作命令而导致电机过热运行。
进一步对电机在 kv取 0.01、0.02、0.03、0.04 且正序电压380 V条件下的三相不平衡电压进行75%负载计算,得到其三相电流随θv的变化关系,最终绘出 Imax/IN与 kv、θv的关系曲面如图 6 所示。 其中,Imax为每一θv对应的最大相电流,IN为额定相电流。由图6可知:定子最大相电流随kv的减小而减小,且在kv=0.04时最坏运行点所对应的最大相电流已达到额定电流。因此,对于文中分析的5.5 kW异步电机在该状况下运行时,其CVUF幅值应不超过0.04。
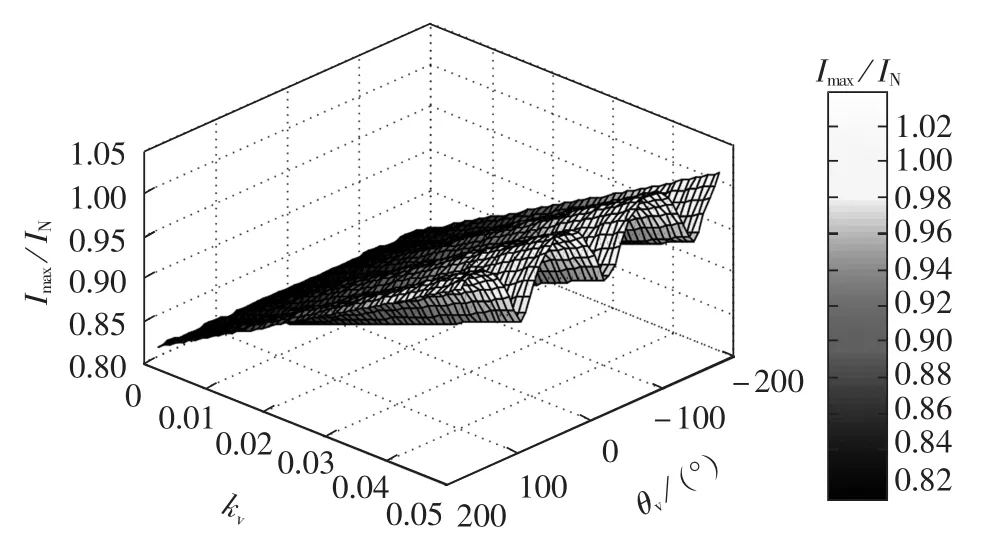
图6 Imax/IN 随 kv、θv的变化关系Fig.6 Imax /INvarying along with kvand θv
4 CVUF相角对损耗的影响
4.1 各项损耗变化规律
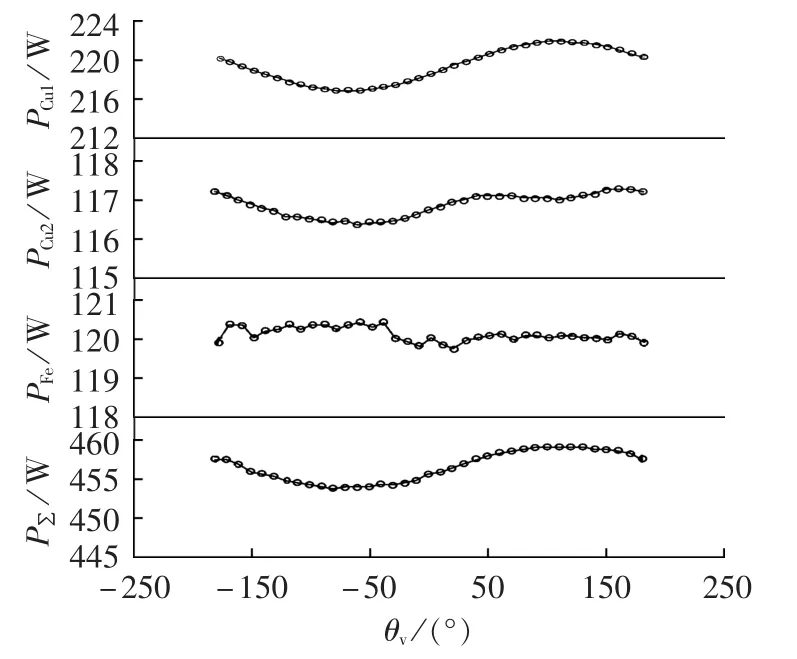
图7 kv=0.05时各项损耗及总损耗随θv变化关系曲线Fig.7 Curves of losses vs.θvwhen kvis 0.05
利用时步有限元法也可计算得到异步电机内部各项损耗,例如,电机带75%负载、kv=0.05且正序电压为380 V时,定子铜耗pCu1、转子铜耗pCu2、铁耗及附加损耗 pFe、总损耗p∑随θv的变化规律如图7所示。从图7可知:定子铜耗变化相对较大,但也低于5 W,其最大值、最小值对应的θv分别近似对应图4中的最佳运行点100°与最坏运行点-80°;此外,对kv取 0.01、0.02、0.03、0.04 时的损耗也进行计算,发现定子铜耗随θv的变化幅度随kv增加而增加,但在相同kv条件下,定子铜耗随θv的变化规律与图7类似;转子铜耗、铁耗变化较小,为1W左右。上述变化仅占电机总损耗的1.1%。
4.2 各项损耗变化原因分析
针对以上各项损耗变化规律进行分析可知,异步电机在kv=0.05、正序电压380 V且带75%负载时有以下特点。
a.从图7中可以看到定子铜耗最大与最小值对应的 θv分别为 110°、-70°,且两者相差 5W 左右,对这2种情况下所对应的定子三相电流进行傅里叶分解可得其基波及各次谐波幅值大小,其对比结果如表2所示,表中,IA、IB、IC及Iav分别为三相不平衡电流及其平均值的幅值,Ieq为三相不平衡电流的等效有效值。由表中数据可知,2种情况下三相不平衡电流均不相等,但3次谐波占基波的比重及Ieq均接近相等,而定子铜耗与定子三相电流有效值的平方和近似成正比,所以定子铜耗变化不大。同样可对θv取其他值时的定子三相电流进行对比分析,结果均与此相同。
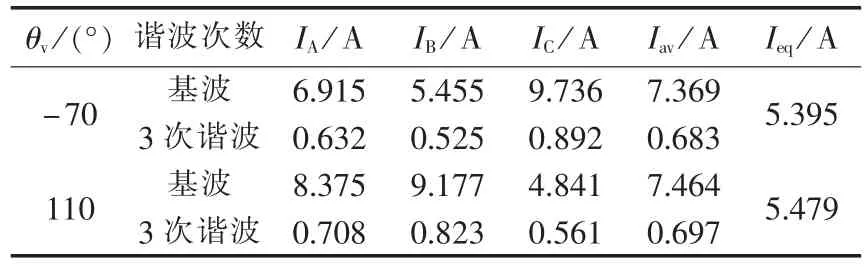
表2 θv为-70°、110°时定子三相电流的傅里叶分解结果Tab.2 Fourier transformation results of three-phase stator currents when θv=-70°and 110°
b.转子铜耗主要与转差率成正比,从图7中可知转子铜耗变化在1 W左右,计算结果显示不同θv时转速接近相等,例如,θv为-80°、100°时的转速差别最大,分别为 1458.4、1456.7 r/min;从转子电流角度分析时,对转子槽顶某位置在 θv为 -70°、110°时的电流密度波形及其傅里叶分析进行对比,结果如图8所示,其中J表示电流密度。由图8可知2种情况下转子槽2、6、18等偶次谐波电流密度变化较小,故转子铜耗基本不变。
c.忽略定子压降的前提下,可认为铁耗与定子绕组端电压的平方近似成正比,电压不平衡时则主要由正序电压或三相电压平均值决定。从图7可见铁耗变化在0.8 W内,且无明显变化规律。从铁芯磁通密度角度分析,对定、转子铁芯齿顶某位置在θv为-70°、110°时的磁通密度波形及其傅里叶分析进行对比,结果分别如图 9、10 所示,图中,Br、Bt分别为径向磁通密度与切向磁通密度。由图9可以看出定子铁芯Br与Bt基波磁通密度幅值相差很小,因此定子铁耗变化不大;由图10可以看出转子铁芯Br与Bt的2、6、12、18等偶次谐波磁通密度变化也较小,因此转子铁耗变化不大,两者综合导致总铁耗基本不变。
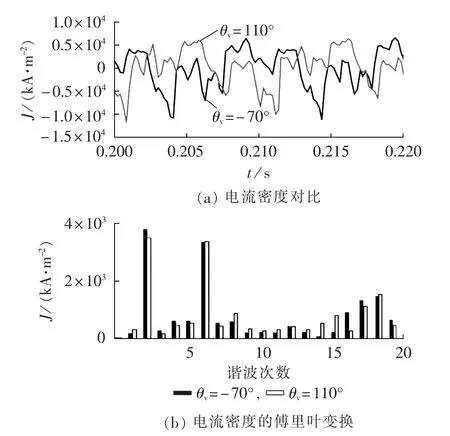
图8 转子槽顶典型位置处电流密度波形及其傅里叶变换结果对比Fig.8 Comparison of current density waveforms and corresponding Fourier transformation results when rotor slot is at typical position
综上可知:电压不平衡时,在CVUF幅值、正序电压及负载相同的前提下,定子三相不平衡电流有效值、转子电流密度各次谐波含量及定转子铁芯磁通密度各次谐波含量总体变化均较小,因此各项损耗随θv变化不大,因此在工程实际中,θv对各项损耗影响可忽略。此外,经计算验证,保持负载及正序电压相同条件下,kv为 0.01、0.02、0.03、0.04 与 kv为0.05时的各项损耗随θv的变化规律均相同,且各项损耗变化量随kv的减小而减小。
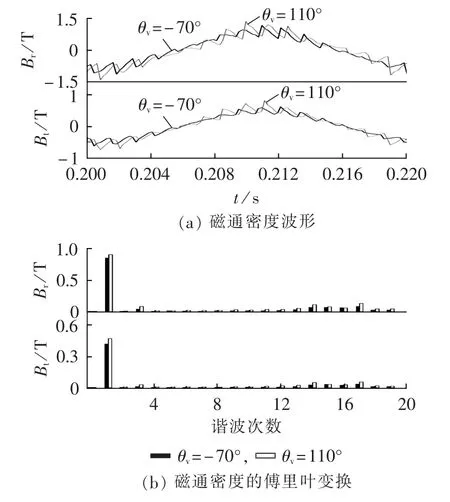
图9 定子铁芯典型位置处磁通密度波形及其傅里叶变换结果对比Fig.9 Comparison of flux density waveforms and corresponding Fourier transformation results when stator core is at typical position
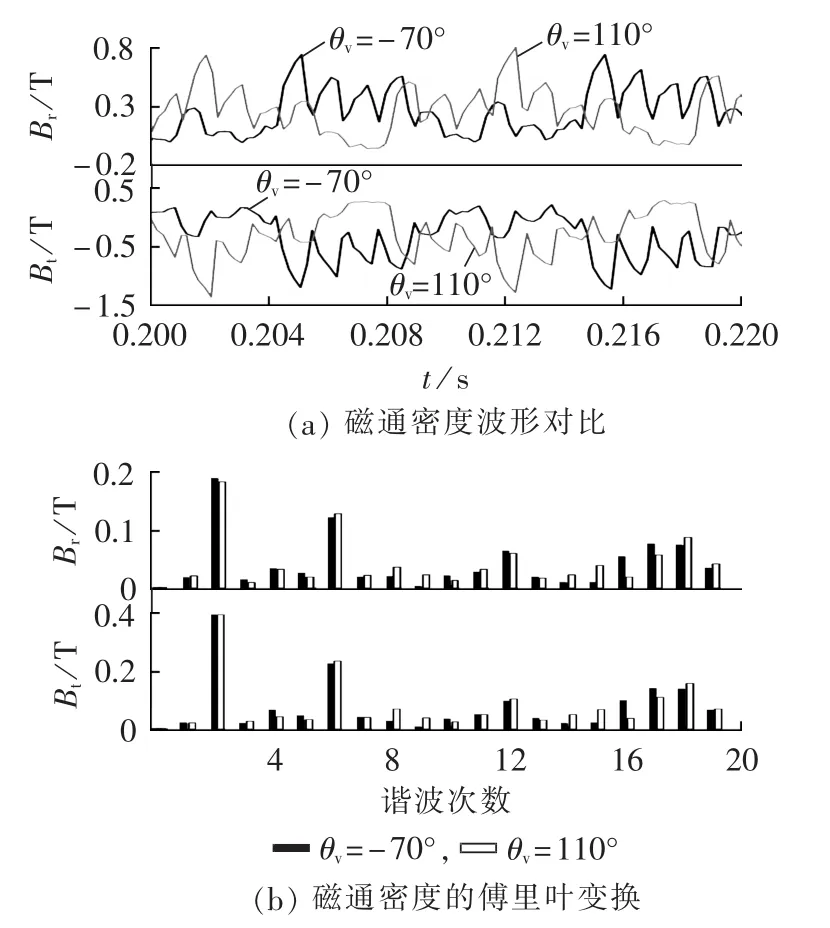
图10 转子铁芯典型位置处磁通密度波形及其傅里叶变换结果对比Fig.10 Comparison of flux density waveforms and corresponding Fourier transformation results when rotor core is at typical position
5 CVUF相角对转矩性能的影响
电压不平衡时,负序磁场将导致异步电机输出转矩减小,为分析CVUF相角对电机转矩性能的影响,在kv=0.05且正序电压380 V前提下,本文选取θv分别为 90°、0°、-90°、-180°4 种条件下的三相不平衡电压,并利用时步有限元法对电机的满载起动过程进行了计算,最终得到这4种情况下的转矩-转速特性曲线及稳态转矩波形,并将其与电压平衡时进行对比,结果分别如图 11(a)、(b)所示。
由图11(a)可知:电压不平衡时,异步电机的最大、最小转矩均有不同程度的减小,如 θv为 0°、-90°、-180°、90°时,最大转矩分别为 101.0、101.3、101.1、101.1N·m,相对平衡时均减小了约3.8%;最小转矩分别为72.5、71.4、71.9、72.8N·m,相对于平衡时分别减小了 1.4%、3.0%、2.3%、1.1%;但是4种不平衡条件下的最大、最小转矩差别较小,最大转矩接近相等,且最小转矩差值保持在1.9%以内。另外,图11(a)中转矩-转速特性曲线在电机起动初始阶段有一定的波动,这主要是由电机内部5、7次谐波磁场综合引起的。综上,可认为CVUF幅值及正序电压相同条件下,CVUF相角对异步电机的最大、最小转矩影响较小。
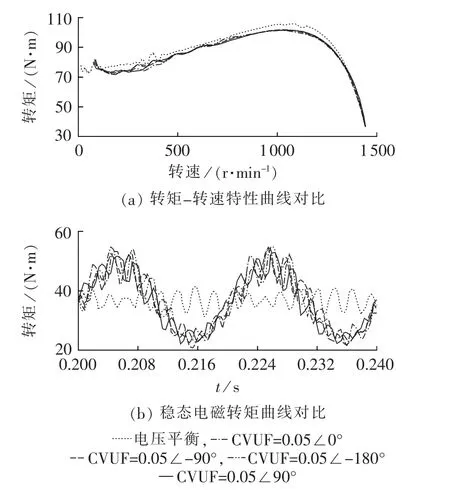
图11 kv=0.05且正序电压380 V与平衡时转矩性能对比Fig.11 Comparison of torque performances between balanced condition and condition that kv=0.05,positive-sequence voltage is 380 V
由图11(b)中可知:电压不平衡时,异步电机稳态电磁转矩存在较大的2倍频脉动分量,例如θv为 0°、-90°、-180°、90°时的 2 倍频脉动分量分别为12.7、12.8、12.5、12.1 N·m,差值保持在 5%以内;另外,受定转子开槽影响,电磁转矩波形中也含有一定的17次谐波分量,例如,电压平衡时电磁转矩为2.5 N·m,电压不平衡情况下,θv为 0°、-90°、-180°、90°时电磁转矩分别为 2.7、2.5、2.5、2.3 N·m,与电压平衡时均相差较小。综上,可认为CVUF相角对电机起动性能及稳态转矩脉动分量影响均较小。
6 实验验证
采用在电机绕组进线端串联电抗器的方式制造某几种电压不平衡条件,利用时步有限元法模拟实测得到的三相不平衡电压及负载,并对仿真与实测结果进行对比。例如,在电机带75%负载且CVUF为0.03∠-73.6°时,定子绕组的实测与仿真三相电流波形分别如图12(a)、(b)所示。其中实测三相电流 ia、ib、ic的有效值分别为 5.14、4.70、6.54 A,仿真三相电流 ia、ib、ic的有效值分别为 5.07、4.70、6.53 A,因此实测与仿真定子三相电流近似相等。
根据GB1032—2012《三相异步电动机试验法》中B法可实测并计算得到电机内部各项损耗[16],并将其与有限元损耗计算结果进行对比。表3中所示为75%负载、kv=0.05时各项损耗的仿真与实测结果对比,由表中可看出电压不平衡时,仿真与实测各项损耗存在一定误差,但总体接近一致。
综上,实测与仿真得到的定子电流及各项损耗基本一致,验证了时步有限元方法及文中分析结论的正确性。
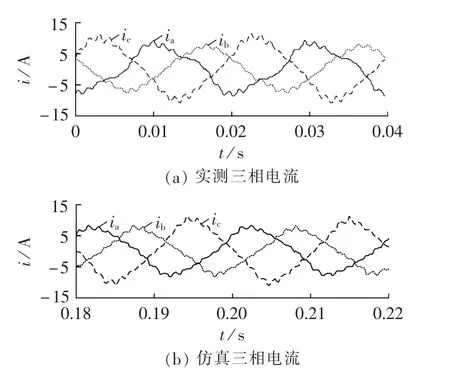
图12 三相定子电流的实测与仿真结果对比Fig.12 Comparison of three-phase stator currentsbetween measured and simulative results
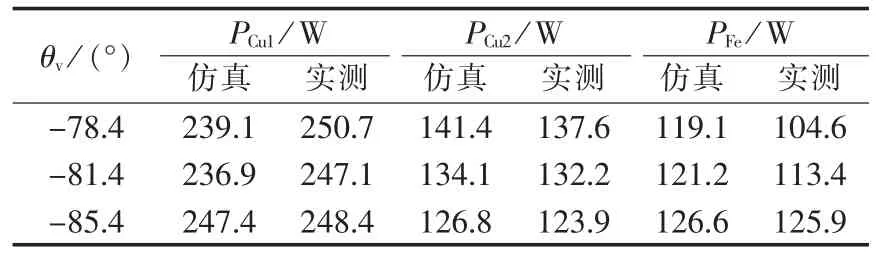
表3 75%负载及kv=0.05时仿真与实测各项损耗对比Tab.3 Comparison of losses between measured and simulative results when load rate is 75%and kvis 0.05
7 结论
本文针对一台5.5 kW异步电机建立了基于时步有限元的损耗计算模型,在给定kv=0.05、正序电压380 V及75%负载条件下,分析了CVUF相角对定子电流、损耗及转矩性能的影响,并验证了文中分析结果的正确性,主要结论如下。
a.定子三相电流随CVUF相角均呈正弦变化规律,为避免绕组过热且使电机保持较高带载能力,应避开最坏运行点。
b.CVUF相角对定子铜耗的影响相对较大,但工程实际中其对各项损耗的影响均可忽略不计。
c.电压不平衡会造成异步电机最大、最小转矩均有不同程度的减小,且稳态电磁转矩中会出现较大的脉动分量,但相同CVUF幅值及正序电压条件下的CVUF相角对其影响均较小。
由于电压不平衡情况较为复杂,且与负载组合状况较多,本文仅针对75%负载及正序电压380V条件下的不平衡电压进行了计算分析,对于其他正序电压及负载条件下的分析将在后续研究中开展。
