基于星形三角形接线多功能平衡变压器的负序和谐波综合治理系统

张志文，陈明飞，胡斯佳，李 勇，王 丹，姜 鹏

（湖南大学 电气与信息工程学院，湖南 长沙 410082）

0 引言

随着近年来我国单相负荷的装机容量不断增大，经单相负荷变电所渗透至公共电网的负序、谐波和无功不断增加，严重威胁公共电力系统的安全稳定运行，污染点周围电力用户也因此无法正常生产和生活，这引起了相关工业部门和学者的广泛关注[1]。

考虑到经济性，为求得电力系统的平衡，我国多数大功率单相负荷的供电系统的进线均采用了相序轮换技术。但对于山区、高原等电网相对薄弱地区的单相负荷供电系统，该方法难以满足国家标准对公共连接点（PCC）电压不平衡度所提出的要求[2]。

采用平衡变压器，是一种抑制由单相负荷引起的负序电流的有效方法，因为该系统具有比非平衡变更强的负序抑制能力。但是平衡变抑制负序的能力受负荷的波动性影响较大，研究结果表明，平衡变两臂的单相负荷越不平衡，其抑制负序的能力越差[3-4]。另外，由于与多数大功率单相负荷引起的负序问题同时存在的还有谐波和功率因数超标（如电气化铁道、单相电弧炉等），平衡变对此无能为力。

采用晶闸管分组投/切的单相静止无功补偿器能对负序和无功进行综合补偿，但该系统在技术和经济上均难以达到理想状态。更为严重的是该系统所采用的无源器件具有易与电网产生串/并联谐振的风险，故其可靠性在本质上存在缺陷[5-6]。

基于上述单相补偿系统的缺点，近20年来，学者和工程师提出了多种基于GTO、IGBT和IGCT等全控型大功率电力电子器件的有源补偿系统。其中受到工业用户广为认可的有静止无功发生器（STATCOM）[7-8]和铁路功率调节器RPC（Railway static Power Conditioner）[9]。

STATCOM主要适用于在单相负荷主变的高压三相电网处进行补偿，考虑到功率器件的耐压水平，STATCOM与高压电网的耦合部分一般需要大容量工频降压变压器（该变压器的容量有时甚至与主变的容量不相上下）[10]，故系统的损耗和投资成本将大幅增加，同时也将增加整个系统的土建和维护成本。STATCOM的另外一种发展趋势是采用多电平技术[11]，采用该技术后可以省去降压变压器，但是整个系统的控制将变得十分复杂。

RPC是一种在电气化铁道单相牵引供电系统中取得成功应用的补偿装置。该系统采用2组单相逆变器背靠背连接，通过重新分配牵引网两相的有功潮流，并分别补偿各相的无功和谐波，能成功应对牵引供电系统几乎所有电能质量问题。与STATCOM类似，为满足功率器件的电压承载能力，牵引网和RPC的耦合部分需采用2台大容量工频单相降压变压器[12-13]，故该系统的成本十分可观，目前仅在国内外少数牵引变电所投入了实际应用[14]。

为弥补上述各补偿系统的缺点，本文提出了一种基于星形三角形接线多功能平衡变压器Y-DMFBT（Y-D Multi-Function Balance Transformer）[15-16]的负序和谐波综合治理系统。本系统充分利用了Y-DMFBT三相变两相和三相变三相的潜能，在将其作为单相负载供电的主变的同时可将辅助降压变压器与主变融合在一起，即从Y-DMFBT二次侧c、d、e三抽头引出低压电源直接与三相全桥型有源系统TPARPC（Three Phase Active Regulation Power Converter）相连。另外，由于Y-DMFBT是一种平衡变压器，与非平衡变压器相比，在两相负载不平衡程度相同时，该系统有源部分调节的功率更低，故系统的可靠性和运行效率也更高。省去辅助降压变压器后整个系统的占地面积将大幅减少，故其土建成本和安装难度将变得更低，系统的集成度得到大幅提高。由于该系统充分利用了Y-DMFBT和TPARPC的潜能，故可以说该系统是一种适用于单相供电系统的具有较高综合性能的电能质量综合控制系统。

1 拓扑结构与接线原理

1.1 拓扑结构

本文所提系统的拓扑结构图如图1所示。该系统由Y-DMFBT作为主变压器为单相负载供电，TPARPC通过3个滤波电抗器与平衡变压器二次侧的三相负载端子（即 c、d、e端子）相连。

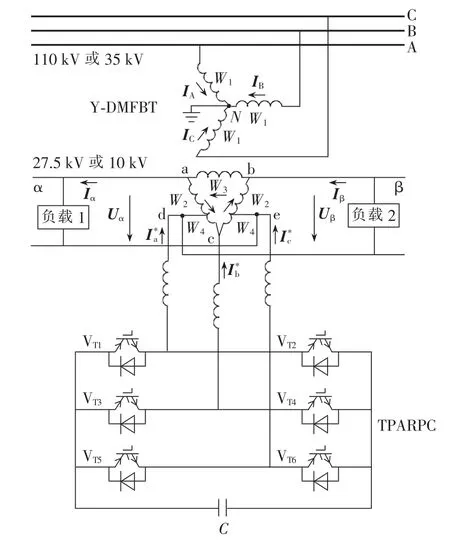
图1 所提补偿系统的拓扑结构Fig.1 Topology of proposed compensation system

在设计时，通过改变Y-DMFBT二次侧d、e抽头处的匝比及阻抗匹配关系，可灵活配置TPARPC的供电电压。这样将大幅降低有源系统中功率器件的负担和控制难度，在不需要多电平技术或者外置降压变压器的情况下即可得到较好的补偿效果。同时在有源系统的制造过程中，系统的散热、损耗及维护成本将大幅降低，可靠性也将得到提高。

1.2 主变基本构成原理

Y-DMFBT既可以给两相负载供电，也可以给三相负载供电。变压器一次侧三相绕组匝数均为W1；A、C相二次侧绕组由2个绕组构成，绕组匝数分别为W2和W4；B相的二次侧绕组由1个绕组构成，匝数为W3。记W1/W2=K，各绕组之间的匝数关系为：

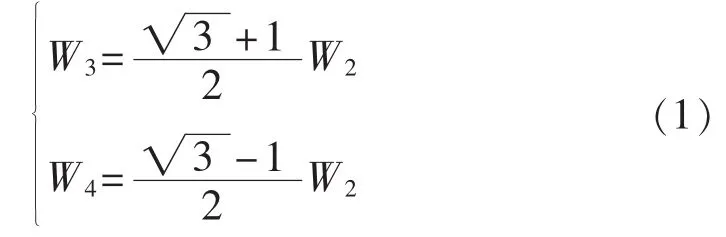
各绕组只需满足如式（2）所示的等值阻抗关系式，则两相之间的电气关系互不影响，即两相解耦。

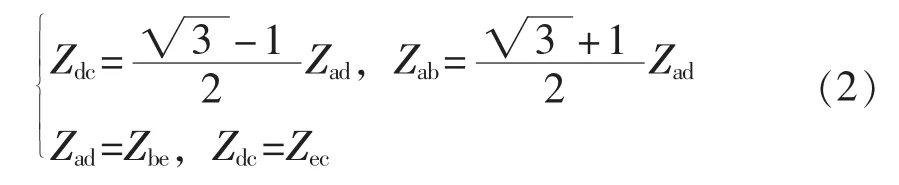
2 系统的补偿原理

在Y-DMFBT中，当单独接两相负载时，一次侧电流和负载端电流满足如式（3）所示关系[15]：

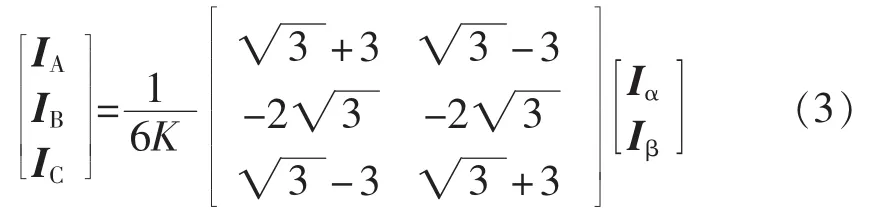
下面将导出当主变仅带有三相负荷时一、二次侧电流的传递关系。

当Y-DMFBT接三相负载时其原理图如图2所示。 对图 2 中 a、d、c、e、b 运用基尔霍夫电流定律（KCL）可得：

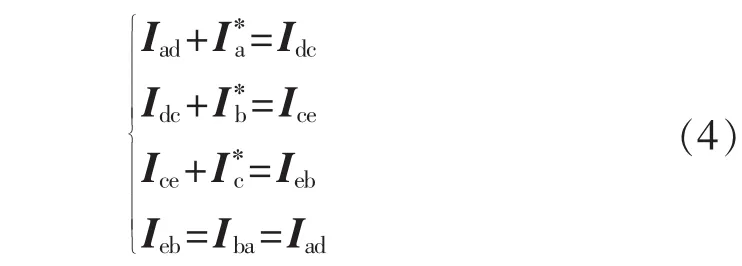
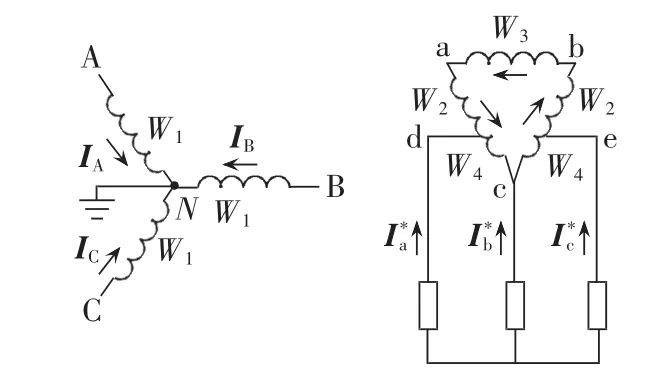
图2 星形三角形接线多功能平衡变压器接星形三相负载Fig.2 Y-D multi-function balance transformer with star-connected three-phase load

在二次侧三角形绕组中由基尔霍夫电压定律（KVL）可得：

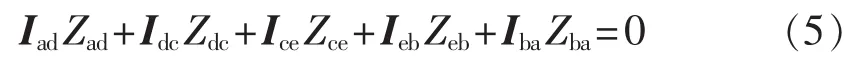
忽略变压器的励磁电流，由一、二次侧磁势平衡关系可得：

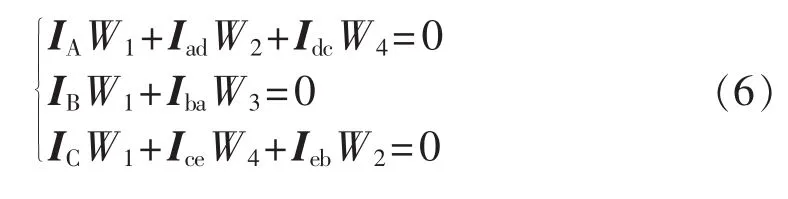
联立式（1）、（2）、（4）—（6）可得：

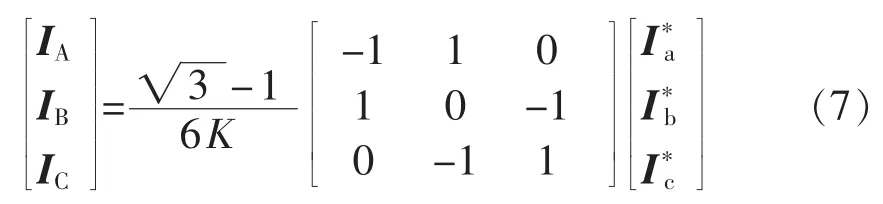
如果Y-DMFBT只接两相负载，而且两相负载平衡，则一次侧不会含有负序和零序电流。同理，如果Y-DMFBT只接三相负载，且三相负载平衡，在一次侧同样也不产生负序和零序电流。但若Y-DMFBT运行在两相负载不对称的场合，一次侧电流中便会出现负序电流。若负载中含有谐波和无功分量，在主变一次侧将会感应出谐波和无功。如果接两相负载的同时，在变压器二次侧的三相负载端接上TPARPC，由叠加定理可得一、二次侧电流传递关系如式（8）所示：

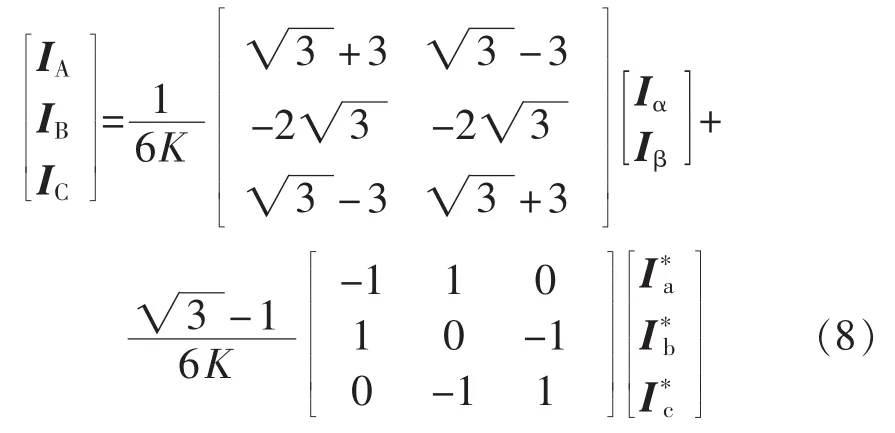
式（8）的瞬时值表达式为：

对于含有负序、谐波和无功分量的负载电流iα（t）、iβ（t），可将其分解成基波有功分量和谐波+无功分量2个部分，即：

其中，iplk（t）、ilk（t）分别为 k（k=α，β）相的基波有功分量和谐波+无功分量。

将式（10）代入式（9）中，可以得到：

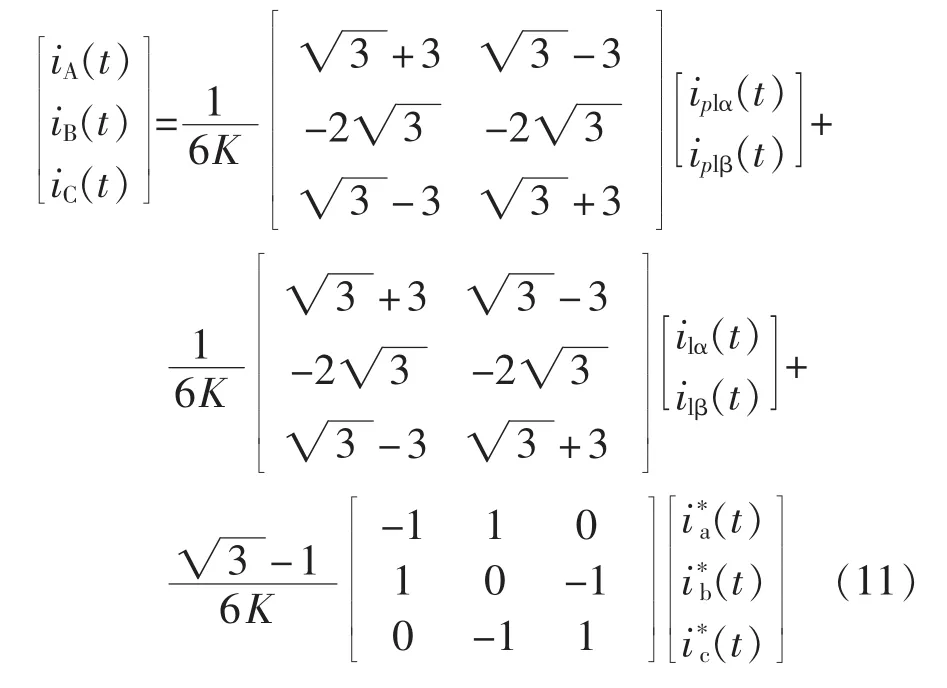
如果式（11）中存在如下关系：

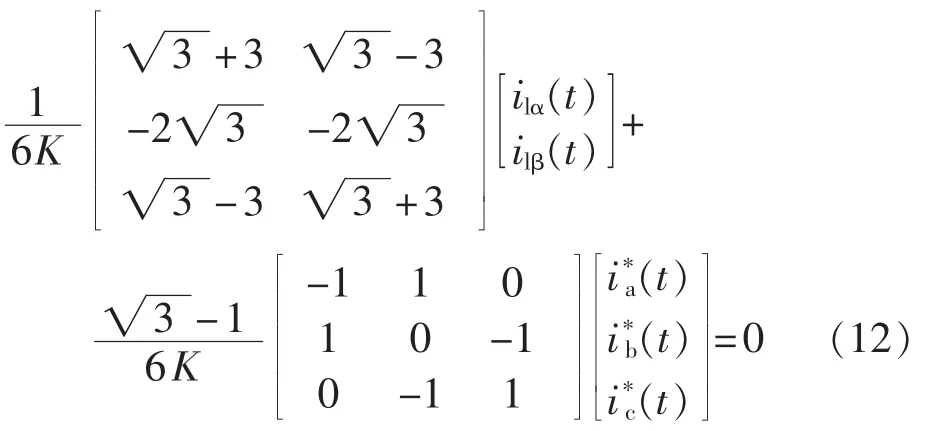
则主变一次侧三相电流将满足式（13）：

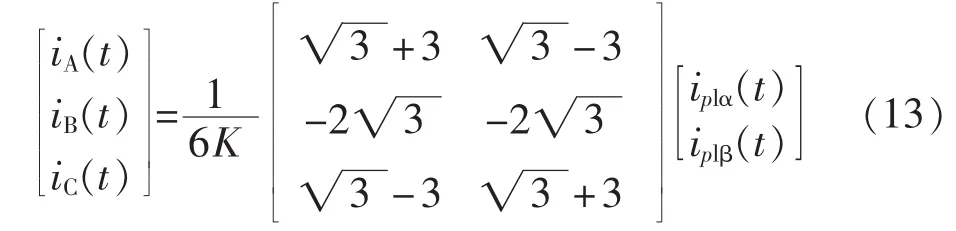
此时式（13）的一次侧电流中只存在基波正序分量，即达到了完全消除一次侧负序、谐波和无功电流的目的。

由式（12）经简单计算可得：

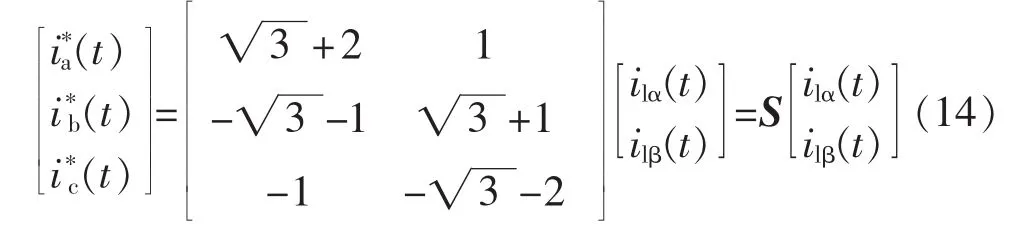
若能将变流器输出电流控制成式（14）的形式，就能实现主变一次侧负序、谐波和无功的完全补偿。

3 系统的控制策略

3.1 检测部分

本系统的检测方法如图3所示，其核心采用基于两相供电电压互差90°的瞬时功率检测方法[17-18]。

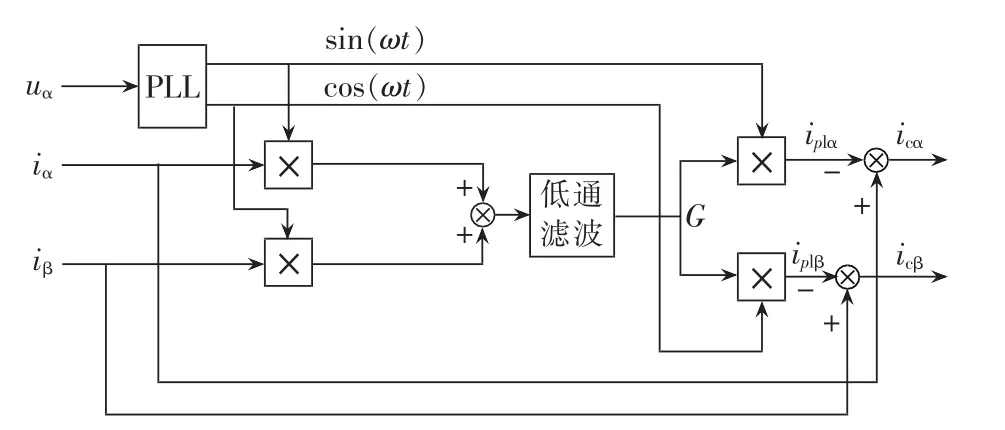
图3 负序、谐波和无功的检测方法Fig.3 Principle of negative-sequence，harmonic and reactive power detection

如图3所示，将α、β相负载电流进行傅里叶分解可得到如式（15）所示的关系：

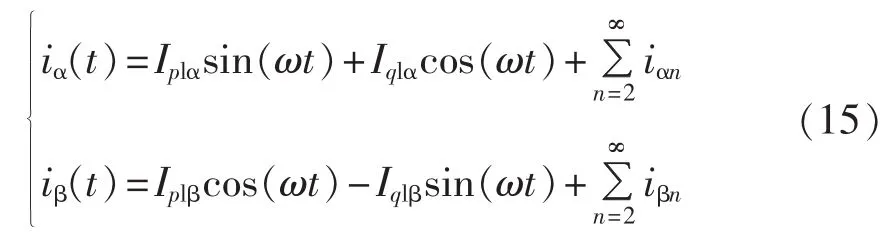
其中，Iplα、Iplβ代表负载电流中的基波有功分量；Iqlα、代表负载电流中的基波无功分量；代表谐波分量。

将式中的 iα（t）、iβ（t）分别乘以与电压相位的同步信号 sin（ωt）、cos（ωt），再将 iα（t）sin（ωt）、iβ（t）cos（ωt）相加，经过低通滤波器可以得到α、β相基波电流有效值的平均值，即：

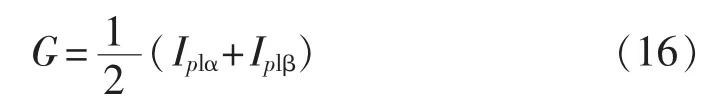
再将 G 分别与 sin（ωt）、cos（ωt）相乘，即可得到α、β相瞬时电流的理想平衡值。该值不再含有谐波和无功分量，并且有效值大小相同。将实际的负载电流瞬时值与理想电流的瞬时值相减，便可以得到所需的补偿电流值 icα、icβ，其表达式如式（17）所示：

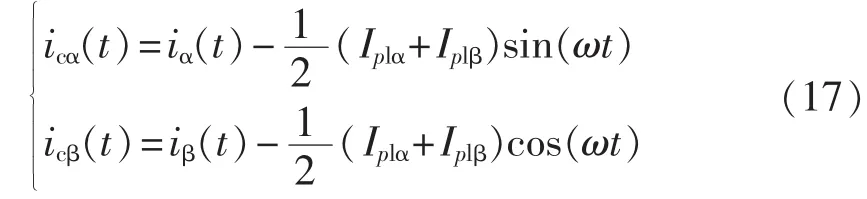
3.2 控制部分

补偿系统的综合控制策略如图4所示。通过检测模块将α相电压的相位信息和两相负载电流的瞬时值经由调理电路输入数字控制器，通过控制器计算出两相负载电流中所含有的负序、谐波和无功分量，并由式（14）计算出TPARPC的指令电流，将指令信号与输出实际电流ia*f、i*bf、i*cf比较之后，通过PI控制器调节，再将其与三角载波进行比较输出功率器件所需要的触发脉冲，从而实现对负序、谐波和无功进行综合治理的目的。

4 仿真分析

为验证本文所提出的补偿系统的正确性，参照图1在MATLAB/Simulink环境下搭建了系统的仿真模型。整个系统仿真参数如下：网侧电压35 kV，二次侧电压10 kV，系统短路容量360 MV·A，变压器容量6.3 MV·A，直流侧电容50 mF，输出电感1 mH，直流侧电压设定值5500 V。

4.1 负载不对称工况

为了验证系统在极不对称负荷条件下的补偿效果。本文中选取β相空载、α相重载作为仿真工况，其中α相负载的具体参数如下：有功功率1.54 MW，无功功率 1.62 Mvar，功率因数0.69，电流谐波畸变率（THD）22.03%。该工况下的仿真结果如图5所示。

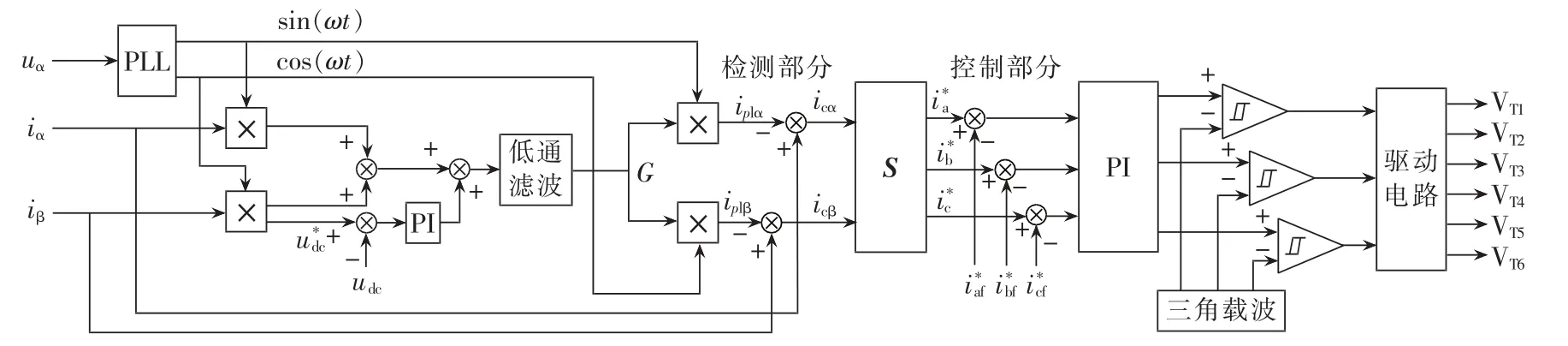
图4 负序和谐波综合治理系统控制框图Fig.4 Block diagram of comprehensive negative-sequence and harmonic suppression system

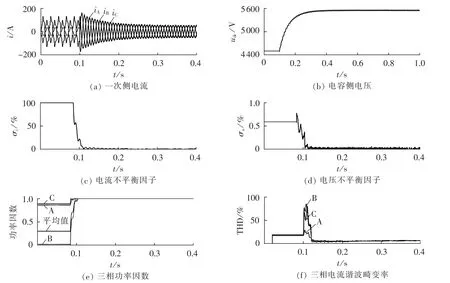
图5 投入TPARPC前后波形及性能对比Fig.5 Comparison of performance and waveform between with and without TPARPC

从图5（a）可以看出，在0.1 s投入TPARPC后，原本不对称且畸变严重的的一次侧电流波形在系统投入半个周期内就成为了三相对称的正弦波，这说明系统具有较好的暂态性能。从图5（c）—（f）可以看出在补偿系统投入后，原系统的电压不平衡度、电流不平衡度、功率因数以及电流谐波畸变率均得到了明显的改善（电压、电流不平衡因子σu、σi分别从0.6%和100%降至0.05%和2%；功率因数接近于1；电流畸变率从20%降至7%以下）。仔细观察还可得知，这几项电能质量指标均在1个周期内达到了稳态，扣除Simulink模块自身的运算时间，它们进入稳态的时间应该小于1个周期。这说明本系统的确能有效应对单相负荷产生的各种主要电能质量问题。另外，从图5（b）可以看出当系统投入后，直流侧电压经过0.3s的调节时间进入稳态，稳态后直流侧电压的稳定情况良好，最大和最小值在指令量1%左右的范围内波动。

4.2 负载变动时的仿真结果

在图6所示的负荷变化时序下，系统的仿真结果如图7所示。负载参数如下：α相负载，有功功率1.54 MW，无功功率1.62 Mvar，功率因数 0.69，电流谐波畸变率22.03%；β相负载，有功功率2.42 MW，无功功率1.89 Mvar，功率因数0.79，电流谐波畸变率16.52%。

图6 负载变化情况时序图Fig.6 Sequence chart during load variation

由图7（a）可知，当负载从单边带负载变成双边带负载时（0.6s），电流能够很平稳地过渡；当突然撤掉β相的负载（0.8s），网侧三相电流仍然能平稳地过渡，在0.2s内进行了2次负载的突变，但是系统的电流基本平稳，这表明在冲击性负荷条件下本系统仍然有比较好的动态性能。图7（b）为与图7（a）相对应的直流电压波形，由图可知，在负荷突变情况下，直流电压的超调量依然不超过5%，这说明本系统的直流电压具有较好的稳定性。图7（c）和图7（d）分别为网侧电流和电压不平衡因子的时序波形，由图可知，其变化波动很小，电流不平衡因子基本上稳定在2%，电压不平衡因子能小于0.1%。由图7（e）可知平均功率因数可以维持在0.98的水平。从图7（f）可以看到，负载每变动一次，一次侧的电流谐波畸变率都会有一定的波动，但是其能够在1～2个周期内趋于稳定，因此对电网系统的影响不大。上述仿真结果验证了该系统应对负荷波动时具有较好的补偿效果。

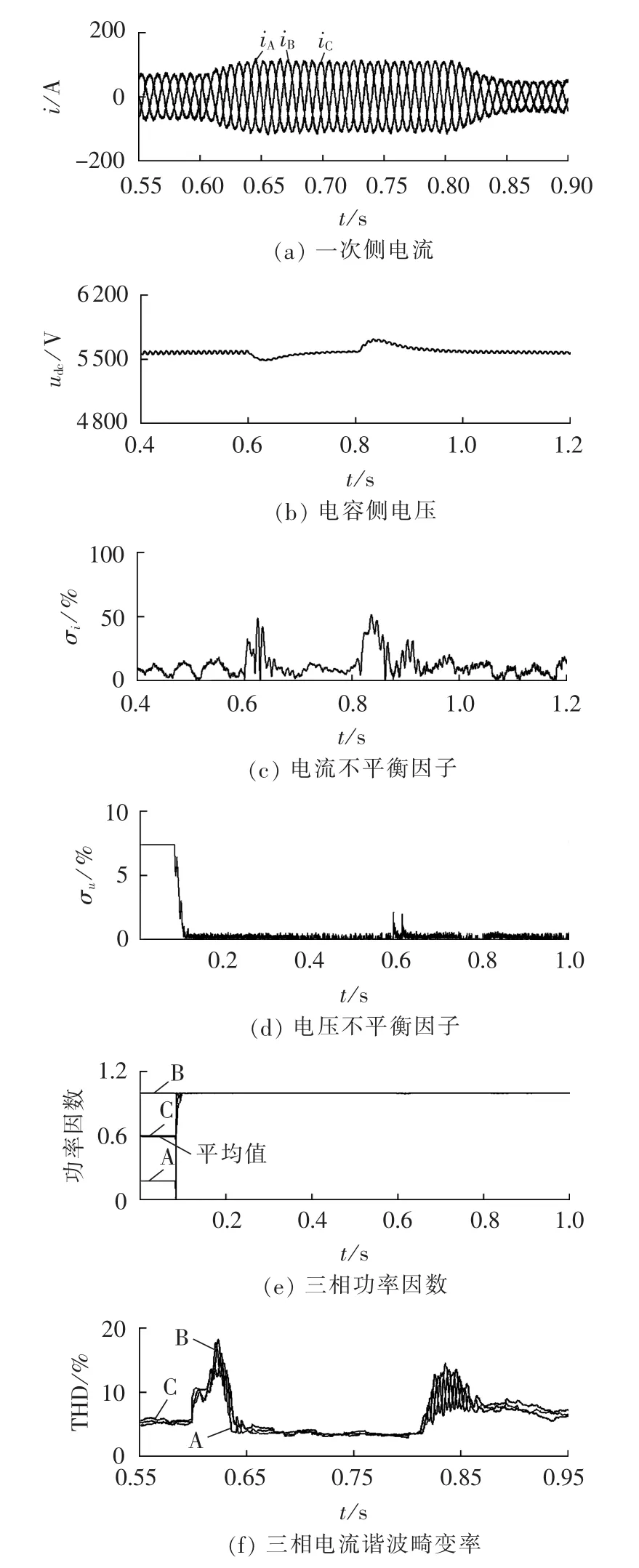
图7 负载波动时投入TPARPC前后性能对比Fig.7 Comparison of performance during load fluctuation between with and without TPARPC

5 实验分析

为了验证本文提出的构想，在实验室搭建了一个380 V电压等级的实物模型。数字控制器采用TMS320F2812；采样频率为12.8 kHz；负载用单相不可控整流桥代替；两相功率分别为Pα=1 kW和Pβ=2 kW；Y-DMFBT容量 5 kV·A；电网电压 380 V；连接电抗 2.5 mH/0.1 Ω，50 A；嘉尚DR50功率模块每相输出17.5 A。波形测量仪器为HIOKI3196电能质量分析仪。

图8给出了投入TRARPC前后变压器一次侧的电流波形。可知，投入前三相电流谐波畸变率的平均值为13.27%，电流不平衡因子为30.26%；投入后电流波形在半个周期内即趋于稳定，三相电流谐波畸变率平均值为6.19%，电流不平衡因子约为2.43%。这说明本系统的治理效果较为明显。

图8 实验波形Fig.8 Experimental waveforms

6 结论

本文提出了一种将Y-DMFBT和TPARPC融合在一起的单相负荷负序和谐波综合治理系统，分析了该系统的补偿原理，并给出了相应的检测及控制算法，对整个系统进行了仿真分析。仿真结果表明该系统能有效抑制供电系统一次侧的负序和谐波电流，提高其受电端功率因数，并通过实验验证了所提系统的有效性。

本文中所提出的系统充分挖掘了Y-DMFBT和TPARPC的潜能，利用Y-DMFBT二次侧三相系统的对称性，在不需要辅助平衡变压器的条件下实现了Y-DMFBT与主变压器的结合，并且成功地对单相负荷供电系统中的负序、谐波和无功进行了综合治理。相比于传统单相供电场合的电能治理系统，该系统在获得相同补偿效果的前提下，无需辅助降压变压器，同时也可以不采用多电平拓扑结构，因此具有较好的成本优势，运行可靠性也得到了提高。因此，所提系统是一种具有较高综合性能的负序与谐波综合治理系统。