改进的Winkler地基桩土相互作用模型①
2014-09-27唐剑华刘振兴
唐剑华, 刘振兴
(1.同济大学土木工程学院地下建筑与工程系,上海 200092;2.岩土及地下工程教育部重点实验室(同济大学),上海 200092)
0 引言
本文在传统的Winkler地基基础上,引进剪力基床系数Kz来考虑桩侧摩阻力,剪力基床系数通过半无限弹性体中的Mindlin解求得.从桩的弹性理论出发,考虑桩顶的集中荷载和桩侧摩阻力,通过对典型单元的受力分析推导桩的挠曲线微分方程,并采用差分法求解该微分方程.
1 基本假设及微分方程
1.1 基本假设
根据以上分析,为建立桩的挠曲线微分方程可作如下假设:
(1)桩及桩周土体均处于弹性工作状态.

图1 典型单元体示意图
(2)桩是柔性桩,桩身均匀,各截面相等.
(3)基于Winkler地基模型把桩视为弹性地基梁,且桩土之间的位移协调.
1.2 桩身挠曲线微分方程
如图1所示考虑长度为d z微分单元体,两端作用,两端作用有弯矩M、剪力H及轴力N,桩侧有土抗力q、侧摩阻力ps,单元体的横向位移为d u.
对图1典型单元体下端中点取矩有:
从图1以上数据可以看出,与全球系统重要性银行相比,当前四大行的资本充足率均低于G-SIBs平均资本充足率(16.32%),四大行面临资本金的制约。资本充足率指标决定了商业银行必须转变发展方式,由原来的“信贷依赖症”、“粗放发展症”,向内涵式集约化追求质量和效益的方式转变。国际上大银行,通过较高的盈利能力留存补充资本,促进贷款投放,形成了资本的良性循环机制。虽然通过发行普通股等方式可以补充资本金,一定程度上缓解资本的压力,但仅仅依靠融资方式补充资本既受制于监管政策,又取决于资本市场的容量,因此,以RAROC为核心,通过改善资产结构、提升资本使用效率是解决问题的根本途径。

式中kh为桩侧土基床反力系数,单位为kN/m2,本文采用vesic[4]提出的方法来确定 .该方法的特点是将基床系数与桩的抗弯刚度、土体的弹性参数和土的泊松比联系起来[5].即:

式中:Es为土体的弹性模量,单位为kPa;v为土的泊松比;EpIp为桩的抗弯刚度,单位为kN·m2;d为桩的直径,单位为m.对于桩侧摩阻力Ps,可定义Ps=kzw,kz可定义为剪切基床系数,kz的单位为kPa,kz的确定方法将在下节详述.
1.3 边界条件的确定
对于顶端自由的桩,桩顶的横向集中力H,轴向力N,弯矩M.故有

对于桩端,除了刚性短桩以外,通常认为桩底的弯矩作用效应是可以忽略的[6,7].因此,桩端边界条件为
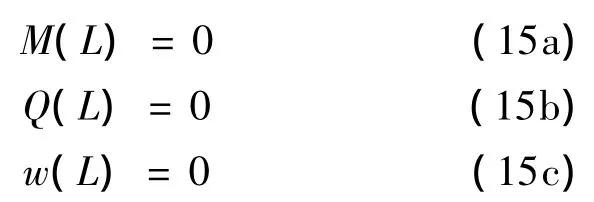

图2 桩侧表面的积分图形
2 基床系数的确定
如图2所示将桩等分成n段,根据polous[8]的思想,按照mindlin解答的基本思路可求出桩侧任意一点的剪力与沉降的关系.由图2可得第i个单元桩侧土的沉降:

式中:w是土体的沉降,h是单元i中点的纵坐标,ρI是位移系数,可由半无限弹性体中的Mindlin解给出,Es是土体的弹性模量.c是桩侧摩阻力所在单元的纵坐标.对(16)式运用积分第一中值定理并考虑到位移系数在c=h处的奇异性[8],化简可得到(16)式.

式(17)中Ps(h)和Es(h)沿着桩身随着深度变化而变化.Iv(h)可由(18)式确定.

式(18)中的 ρI可由 Mindlin解[9]给出

式中 z1=h - c,z2=h+c,r=2R sin(θ/2),
由(17)式可得

式(20)中kz(h)=Es(h)/d Iv(h),经上述分析可得到剪力基床系数kz.
3 有限差分解
利用有限差分法,将微分方程(10)、(11)、
(12)、(15)离散得到代数方程.


式中δh=L/n,离散后的代数方程是非线性的代数方程组,可采用Newton-Raphson方法求解.

图3 桩顶作用水平力

图4 竖向基床系数分布图
4 算例验证
算例1:为说明计算方法的实用性,本文与Poulos的弹性理论法[8]对比,如图3所示,计算时桩长与直径比为L/d=25,桩的柔度系数为kR=EpIp/EsL4,土的泊松比 v为0.5,桩顶自由,桩顶作用水平力.本文方法与Poulos的分析一致,在桩身刚度较小的时候,本文方法得到的桩身弯矩.
由本文方法可得到剪力基床系数Kz随深度的分布.图4是竖向基床系数Kz的分布图.从桩顶到桩身,Kz呈非线性的分布,随着深度的增加,Kz先减小,后逐渐增大,且在靠近桩端的部分,Kz增加的较快.此外,由图4还可知道,随着泊忪比v的增大,剪力基床系数减小,但泊忪比v对剪力基床系数的影响较小.

图5 桩身弯矩

图6 桩身水平位移
算例2:计算参数如下:取桩长与直径比 L/d=25,土的泊松比v=0.25,桩土弹性模量比Ep/Es=1000,桩顶作用的水平力和轴力分别为H=πGsd2,N=0.2H,0.5H,H,Gs为土体的剪切模量.
从图5中可以看出本文方法得到的弯矩比polous得到的弯矩偏大,这是因为本文考虑了侧摩阻力的影响.从图5中还可知道,轴向荷载对桩身弯矩的影响主要集中在桩身上部Z/L=0~0.4的范围内.Z/L约等于0.2处,弯矩取得最大之.随着N/H的增大,最大弯矩逐渐增大.当N=0.5H时,最大弯矩增加10.4%;当N=H时,最大弯矩增大32.8%.
从图6中可看出,当N/H的值较小的时候,N/H的值对桩身挠度的影响较小.当N/H的值较大的时候,随着N/H的增大,p-Δ效应显著,桩身挠度显著增大.桩身的侧向挠度主要集中在Z/L=0~0.6范围内.
5 结语
本文在传统的Winkler地基基础上,引进竖向基床系数Kz来考虑桩侧摩阻力,并得到了竖向基床系数随深度的分布图.随着深度的增加,竖向基床系数显著地增大.本文在引进竖向基床系数的基础上,计算表明,忽略侧摩阻力会使桩身弯矩偏小,在设计中会带来潜在的风险.
[1]赵明华.轴向和横向荷载同时作用下的桩基计算[J].湖南大学学报,1987,14(2):69 -81.
[2]Yun Tian - quan.Pile Analysis by Simply Integral Equation Method[J].Appl,Math&Mech,1981,2(3):2(3):331 -348.
[3]赵明华.倾斜荷载下基桩的受力研究[J].湖南大学学报,1997,24(2):98 -102.
[4]Vesic AS.Bending of Beams Resting on Isotropic Elastic Solids[J].Journal of Soil Mechanicals and Foundation Engineering,ASCE,1961,87(2):35 -41.
[5]梁发云,于峰,黄茂松.受土体侧移作用既有轴向受荷单桩的简化算法[J].同济大学学报,2011,39(6):807-813.
[6]PAK R Y S.On the Flexure of a Partially Embedded Bar Under Lateral Loads[J].Journal of Applied Mechanics,1989,56(2):263–269.
[7]CHEN S L,CHEN L Z.Note on the Interaction Factor for Two Laterally Loaded Piles[J].Journal of Geotechnical and Geoenvironmental Engineering,2008,134(11):1685–1680.
[8]Hiroyoshi Hirai.A Winkler Model Approach for Vertically and Laterally Loaded Piles in Nonhomogeneous Soil[J].Int.J.Numer.Anal.Meth.Geomech.2012,36:1869 – 1897.
[9]RAYMOND D.MINDLIN.Force at a Point in the Interior of a Semi- Infinite Solid[J].Journal of Physis,1936,7(2):195 -202.
[10]陈海兵.横向与竖向荷载作用下单桩分析方法及两桩相互作用系数研究[J].上海:同济大学,2011.
