含DFIG风机的电力系统次同步谐振附加阻尼控制器设计

张宋彬，江全元，陈跃辉，张文磊，宋军英

（1.浙江大学 电气工程学院，浙江 杭州 310027；2.湖南省电力公司，湖南 长沙 410007）

0 引言

近年来，越来越多的风电接入电力系统中，据统计，在2010年，全世界总的风电装机容量增加了23.6%[1]。随着风电注入功率的增加，需要建设新的传输线路或者提高现有输电线路的传输极限。通常提高线路传输极限的方法是在线路中串补电容。但是，输电线路的不恰当串联电容补偿不仅会引起电力系统“自励磁”运行状态的发生，还可能会诱发一种更严重的机电耦合振荡——次同步谐振SSR（SubSynchronous Resonance）[2]。

近年来发现，DFIG风机经串补线路接入系统中，系统容易发生SSR，而SSR会对DFIG风机造成严重的损坏[3]。所以，对含DFIG风机的SSR的研究十分必要。

SSR现象通常包括感应发电机效应IGE（Induction Generator Effect）和机电扭振互作用 TIE（Torsional Interaction Effect）[2]，由于在 DFIG 风机和串补网络之间的TIE只有当串补很高时才会发生[4]，所以TIE不是本文研究的重点。本文主要研究IGE，因为它是引起SSR的主要原因。

文献[4-5]通过特征值分析，得出SSR现象与线路串补度、风速以及转子侧的PI控制参数有密切的关系，但是没有提出SSR的治理方法。当前治理SSR最为常用的方法是通过FACTS器件附加一些控制策略[6-8]；文献[6-7]通过调节可控串补（SSSC）控制，提高串补网络的阻尼进而抑制SSR，但是只是针对传统发电机的SSR问题；文献[8]通过在风电场出口处并联接入STATCOM，进而抑制SSR和功率波动，但是风电场中的风机是恒速风机，并不包含DFIG风机。文献[9]通过在DFIG风机的网侧控制器附加阻尼控制来治理SSR，结合了DFIG风机的特点，提出了相应的控制策略，但是没有考虑转子侧PI控制参数对SSR的影响。

分析SSR的方法大多数基于特征值[4]，通过状态空间表达式来得到系统的特征矩阵，进而分析系统的稳定性。本文采用阻抗分析方法，相比状态空间法有如下优点[10]：当独立的电源和负载的阻抗模型已经建立时，系统的阻抗模型就很容易得到；增加或减少一个电源、负载，或者改变负载的运行模式，只影响对应的阻抗支路，对系统阻抗模型影响很小；一个元件的阻抗模型可以通过实验的方法得到；当系统存在稳定性问题时，阻抗分析法可以比较方便地给出可能的解决方法。

本文在文献[5，11]的基础上，基于阻抗分析方法，提出了一种在转子变流器侧附加阻尼控制器的方法。该控制方法能够很好地抑制SSR，同时由于考虑了SSR的振荡频率，相比于在网侧附加SSR阻尼控制器（SSRDC），在转子侧内环电流控制附加SSRDC抑制SSR的效果更好。最后，在MATLAB/Simulink环境下搭建仿真系统，验证了该阻尼控制器抑制SSR的作用。

1 基于阻抗分析的奈奎斯特稳定判据

把被研究的系统分割成2个子系统，即电源子系统和负载子系统。电源子系统的戴维南等效电路为一个理想电压源Us串联一个输出阻抗Zs，而负荷子系统的模型为阻抗Zl，如图1所示。几乎所有的电力电子电路均为非线性的，所以这种线性化的表达形式只适用于小信号分析。

图1 电压源和负载连接的小信号模型Fig.1 Small-signal model of voltage source with load

对于假定的小信号模型（图1所示），从电源流向负载的电流为：

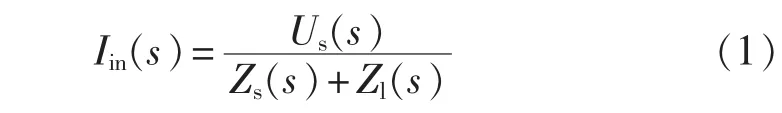
式（1）可以写成：

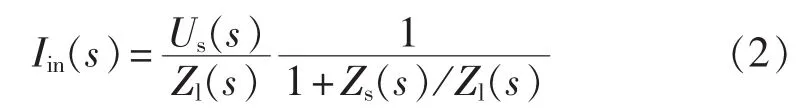
式（2）可以用图2所示的传递函数形式来表示。

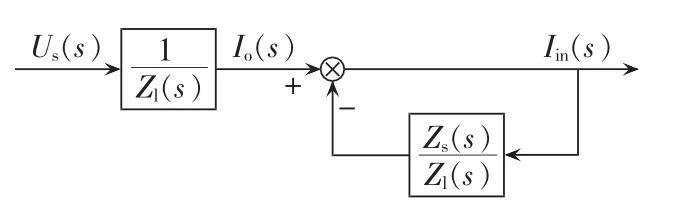
图2 电压源和负载连接的小信号模型传递函数框图Fig.2 Transfer function of small-signal model of voltage source with load

对于图2所示的系统，稳定的前提为下述的3个条件同时满足：电源的输出阻抗为零、负荷的输入阻抗为无穷大、在所有的频率下都成立。但该条件是充分不必要的条件，下面介绍系统稳定的充分必要条件[11]。

如图2所示，其传递函数为：

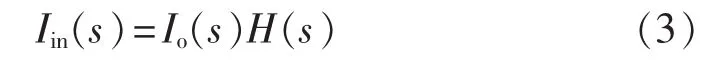
其中，Io（s）=Us（s）/Zl（s），H（s）=1/[1+Zs（s）/Zl（s）]。

如式（3）所示，分析系统的稳定性只需要分析闭环传递函数H（s）的表达式即可。根据自动控制理论可知，闭环系统的稳定性可以通过其开环频率响应Zs（jω）/Zl（jω）曲线对（-1，j0）点的包围与否来进行判别[12]，即奈奎斯特稳定判据。

a.如果开环系统是稳定的，即分母的所有零点均在s域的左半平面时，则其闭环系统稳定的充要条件是 Zs（jω）/Zl（jω）曲线不包围（-1，j0）点。

b.如果开环系统不稳定，且已知有P个开环极点在s域的右半平面，则其闭环系统稳定的充要条件是 Zs（jω）/Zl（jω）曲线按逆时针方向围绕（-1，j0）点旋转P周。

大多数系统的不稳定发生在 Zs（jω）/Zl（jω）包围（-1，j0）点的时候。假设系统存在一个频率 ω0使得Zs（jω0）/Zl（jω0）是纯实数，且小于 -1，则有：

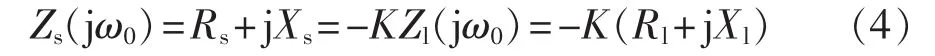
其中，K＞1，且是一个实数，所以：

由式（4）和（5）可得，在某一频率下，应用奈奎斯特稳定性判据判定的系统不稳定等价于该系统具有等效的负电阻。

2 系统阻抗模型

本文采用的研究系统如图3所示，单台1.5 MW的DFIG风机经变压器接入25 kV的串补线路，XTg代表网侧变流器（GSC）的感性滤波器[13]。下面将介绍各部分的阻抗模型。

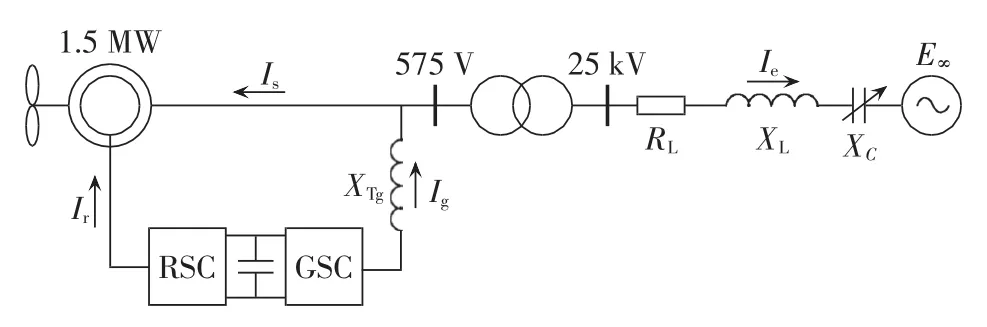
图3 DFIG风机经串补接入无穷大系统结构图Fig.3 Structure of DFIG connected to infinite system via series-compensated network

2.1 RLC线路的阻抗模型

假设串补线路三相对称，且不考虑该线路的互感，则对于三相RLC电路的矢量空间（abc坐标系）表达式如式（6）所示：

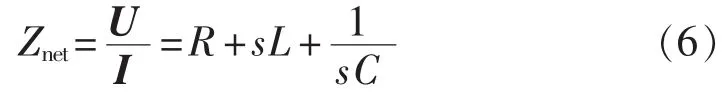
2.2 异步电机的阻抗模型

异步电机的dq0模型[14]如图4所示，根据dq坐标系下的异步电机电路可得[5，15]：

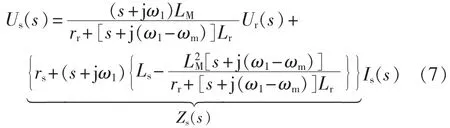
式（7）是基于dq坐标系，串补线路RLC的阻抗模型是基于abc坐标系，根据dq坐标系和abc坐标系之间的关系式（8），异步电机在abc坐标系下的阻抗模型如式（9）所示。

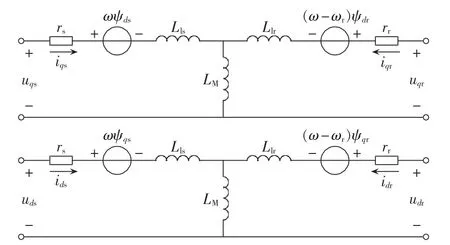
图4 dq坐标系下异步电机的电路Fig.4 Circuits of induction machine in dq axises

由式（9）可得异步电机的阻抗模型等效电路图（等效戴维南电路）如图5所示。

图5 异步电机的等效戴维南电路Fig.5 Thevenin equivalent circuit of induction machine

2.3 变流器阻抗模型

DFIG风机变流器控制采用级联控制[16-17]，控制回路包含内环电流控制和外环功率/电压控制，如图6所示。内环电流控制的控制速度很快，频带接近或高于100 Hz；而外环控制的控制速度较慢，频带只有几赫兹[5]。对于SSR而言，其响应速度远快于外环的功率/电压控制，外环控制可以认为在发生SSR时不起作用，因此在分析SSR现象时，可以不考虑外环控制。

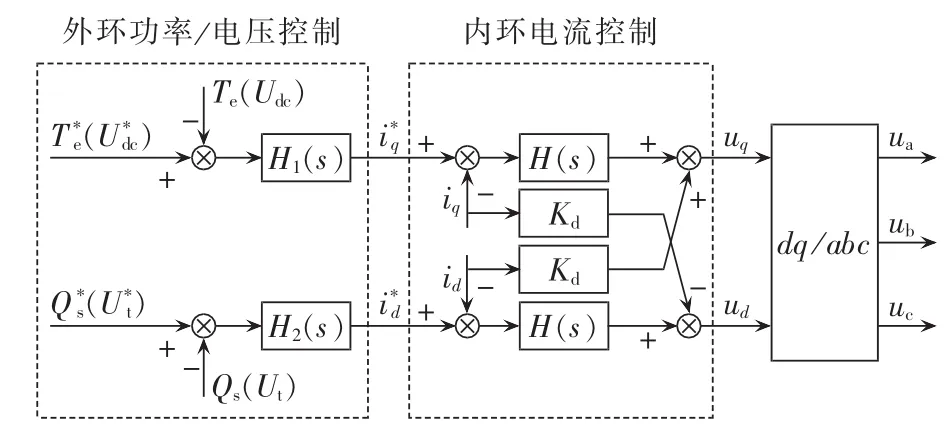
图6 变流器控制回路Fig.6 Control loop of converter

如图6所示，按照类似异步机推导过程可得：

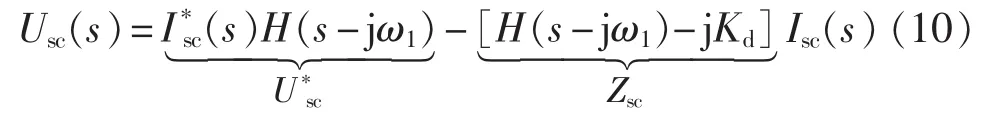
由式（10）可得，GSC 和转子侧变换器（RSC）的等效阻抗模型电路图（戴维南电路）如图7所示。

对于GSC侧：

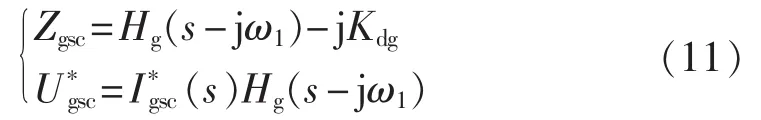
对于RSC侧：

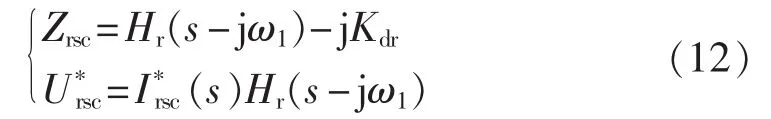
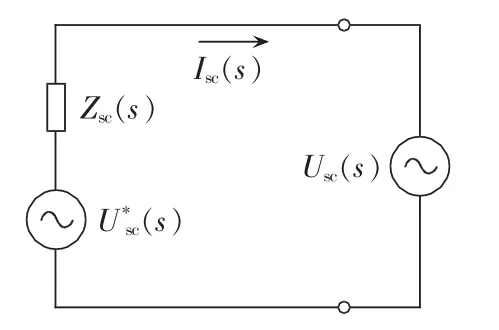
图7 GSC和RSC的等效戴维南电路Fig.7 Thevenin equivalent circuit of GSC and RSC

2.4 整个系统的等效电路模型

由2.1、2.2和2.3节内容可得到如图8所示的整个系统的等效阻抗模型。该模型包含两部分阻抗：DFIG风机阻抗ZDFIG和串补网络阻抗Znet。

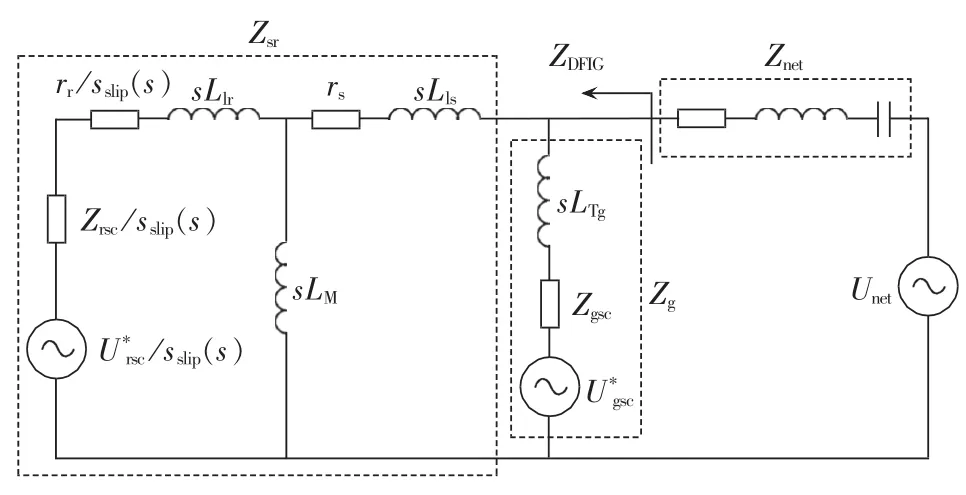
图8 整个系统的等效电路图Fig.8 Equivalent circuit of overall system

由转差率 sslip的定义可知，sslip=1-ωm/ω1，在 s平面下，转差率的表达式变为：

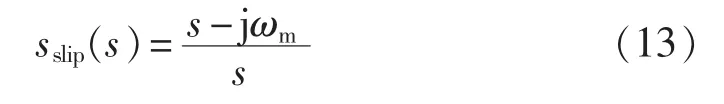
线路的谐振频率为：

其中，XL和XT分别为线路电抗和变压器电抗；XC为串联电容容抗。一般而言，在SSR谐振频率下，Zg的幅值远大于Zsr的幅值[5]，所以以下的分析均忽略Zg所在的支路。

2.5 谐振频率下SSR对DFIG风机的影响

当线路谐振频率为fn时，时域下转差率的表达式为：

其中，fN为系统额定频率，因为 fn＜fN，所以 sslip＜0，即异步发电机的转子电阻为负。此时系统的等效电阻为：

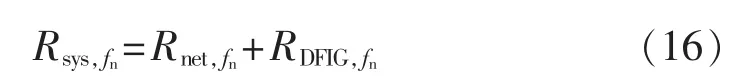
当线路的串补度不同时，fn不同，系统的等效电阻也不同。线路接入的串补度越高，fn越接近fN，sslip越小，转子电阻 Rr/sslip负阻尼越大，则 RDFIG，fn负阻尼也越大。 如果RDFIG，fn负阻尼过大，则可能导致Rsys，fn呈现负阻尼，系统振荡将加剧，最后失去稳定。

如图9所示（U为标幺值），当串补度δSC=70%时，DFIG风机出口处的电压幅值振荡幅度达到近2倍的额定电压，如此高的电压，势必对风机造成危害。同时风机的撬棒回路的启动导致机器的自激励，风机中的电力电子控制作用导致了负阻尼和系统不稳定性的进一步加深[3]，致使电压振荡加剧，如此产生恶性循环，又加剧了对风机的影响。

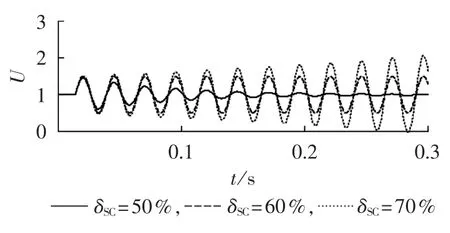
图9 DFIG风机端电压幅值Fig.9 Voltage amplitude of DFIG terminal

2.6 风电场下系统的等效阻抗模型

如图10所示，由N台DFIG风机构成的风电场，经高压串补线路输送到无穷大系统。首先根据2.1—2.4节的方法建立所有DFIG风机的等效阻抗模型（等效阻抗为 ZDFIGi（i=1，2，…，n）），进而可以得到整个风电场的等效阻抗模型：

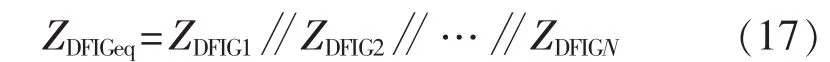
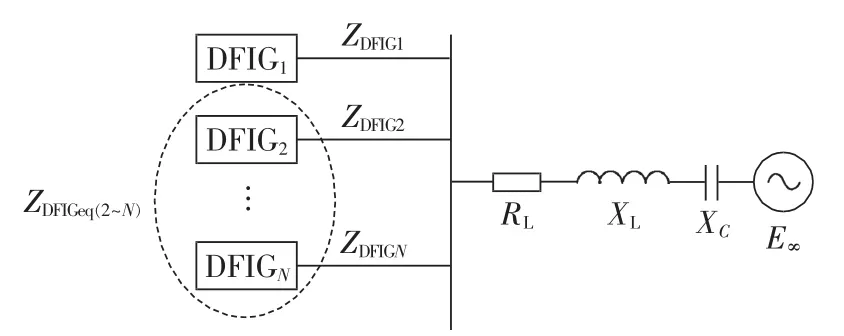
图10 N台DFIG风机构成的风电场经串补线路接入无穷大系统Fig.10 Connection of N DFIGs to infinite system via series-compensated network

如果分析SSR对任意一台风机（假设第1台风机）的影响，只需要将除了这台风机以外的所有风机（2～N）等效为一台风机 ZDFIGeq（2～N），第 1 台风机单独考虑，如图10中所示。当δSC=50%时，所有风机单独考虑与该方法等效考虑的对比如图11、12所示。

图11、12的仿真结果都是第1台风机的电磁转矩Te（标幺值），可知，该等效方法很好地符合实际情况，能够用于分析SSR对任意一台风机的影响。

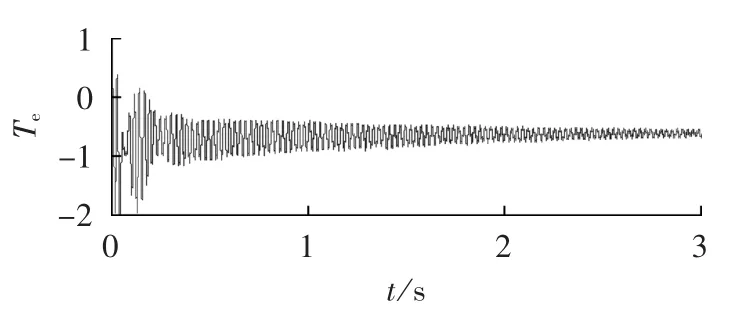
图11 DFIG风机单独考虑的仿真结果Fig.11 Simulative result when single DFIG is considered

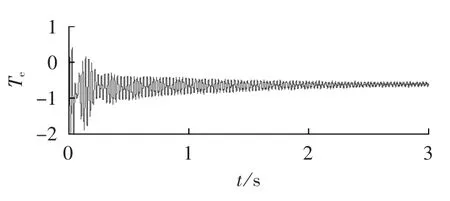
图12 DFIG风机等效考虑的仿真结果Fig.12 Simulative result when all DFIGs are equally considered

3 附加SSR阻尼控制器的设计

考虑到 SSR 的谐振频率范围 10～40 Hz[18]，同时考虑RSC内外环的动态响应频率，为抑制SSR，提出在RSC的内环电流控制中附加SSRDC，如图13所示。

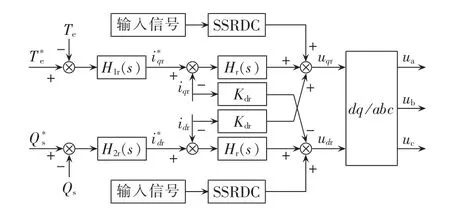
图13 RSC侧电流内环附加SSRDCFig.13 SSRDC added to inner control loop of RSC

3.1 SSRDC结构设计

文献[4]中提到，风速以及线路串补对SSR具有很大的影响，所以本文提出以风机转速偏差Δωm作为控制器的输入信号，将Δωm反馈引入RSC控制的内环中。

SSRDC采用超前-滞后校正模型，其传递函数如下[16]：

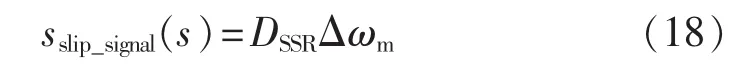
3.2 基于PSO算法优化SSRDC的控制参数

如图3所示的系统，附加SSRDC控制后的阻抗模型如图14所示。由2.4节内容介绍可知，系统的开环传递函数Znet/Zsr为：

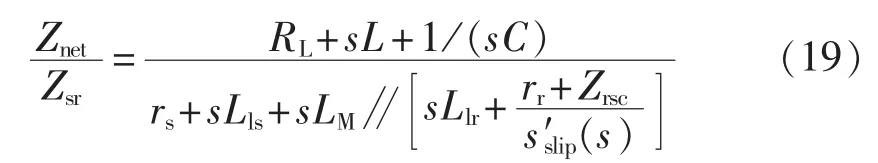
根据 3.1 节的分析可得 s′slip（s）的表达式为：

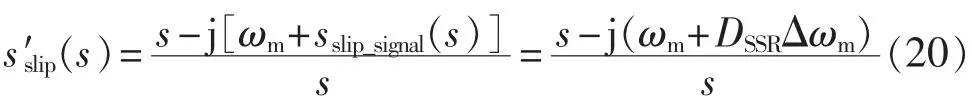
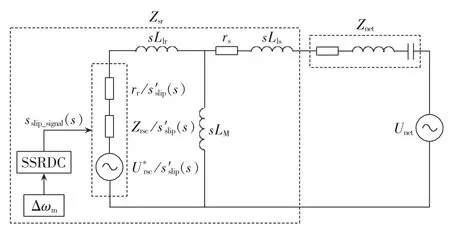
图14 附加SSRDC系统的等效电路图Fig.14 Equivalent circuit of system with additional SSRDC

根据奈奎斯特稳定判据，分析系统的开环传递函数Znet/Zsr的奈氏曲线，可以得到系统的增益裕量Kg和相位裕量γ，由于工程上通常要求γ在30°～60°之间[12]，而增益裕量越大越好，所以本文优化的目标函数为：

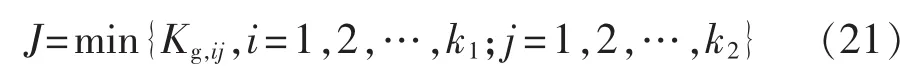
其中，Kg，ij为在第i种串补度、第j种风机转速下的增益裕量；k1为串补度数；k2为不同风机转速数。附加SSRDC后希望J尽可能的大，为此可将优化问题描述如下：

其中，KSSR∈[0.1，100]；时间常数τ1和τ3取值范围为[0.01，1]s[17]。 保持系统稳定，附加如下 2 个约束：

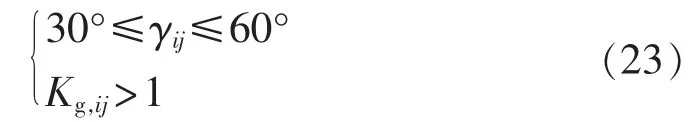
其中，γij为在第i种串补度、第j种风机转速下的相位裕量。

本文调用粒子群优化（PSO）算法解决上述优化问题，经优化计算得到KSSR、τ1、τ3值分别为26.434、0.113 s、0.059 s，目标函数 Jmax=5.561。

附加SSRDC采用上述优化出的参数值，附加该控制器后，系统的开环传递函数Znet/Zsr在不同风机转速下和不同串补度下的奈奎斯特曲线如图15和图16所示。如图15（a）所示，在不同串补度下，当不加 SSRDC 时，Znet/Zsr的奈奎斯特曲线包围（-1，j0）点，此时系统不稳定；如图15（b）所示，当附加该控制器后，该曲线不包围（-1，j0）点，此时系统稳定。因此对比图15（a）和15（b）可得结论：在不同串补度下，该控制器都能够有效地抑制SSR。如图16（a）和16（b），同理分析可得结论：在不同风机转速下，该控制器同样能有效地抑制SSR。综合以上分析可知，附加SSRDC能够有效地抑制系统的SSR。

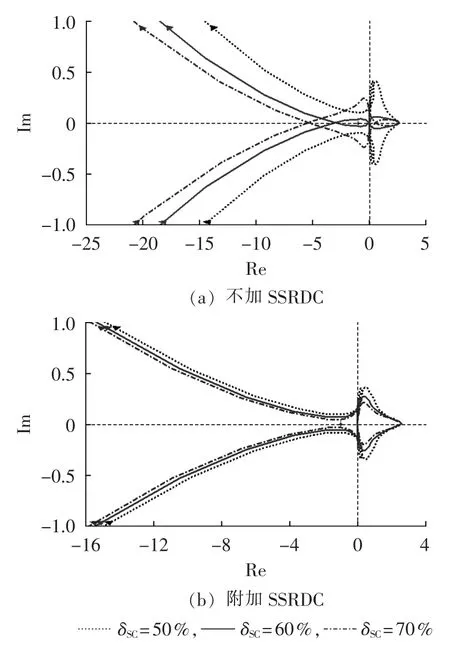
图15 不同串补度下Znet/Zsr的奈奎斯特曲线Fig.15 Nyquist curves of Znet/Zsrfor different δSCvalues

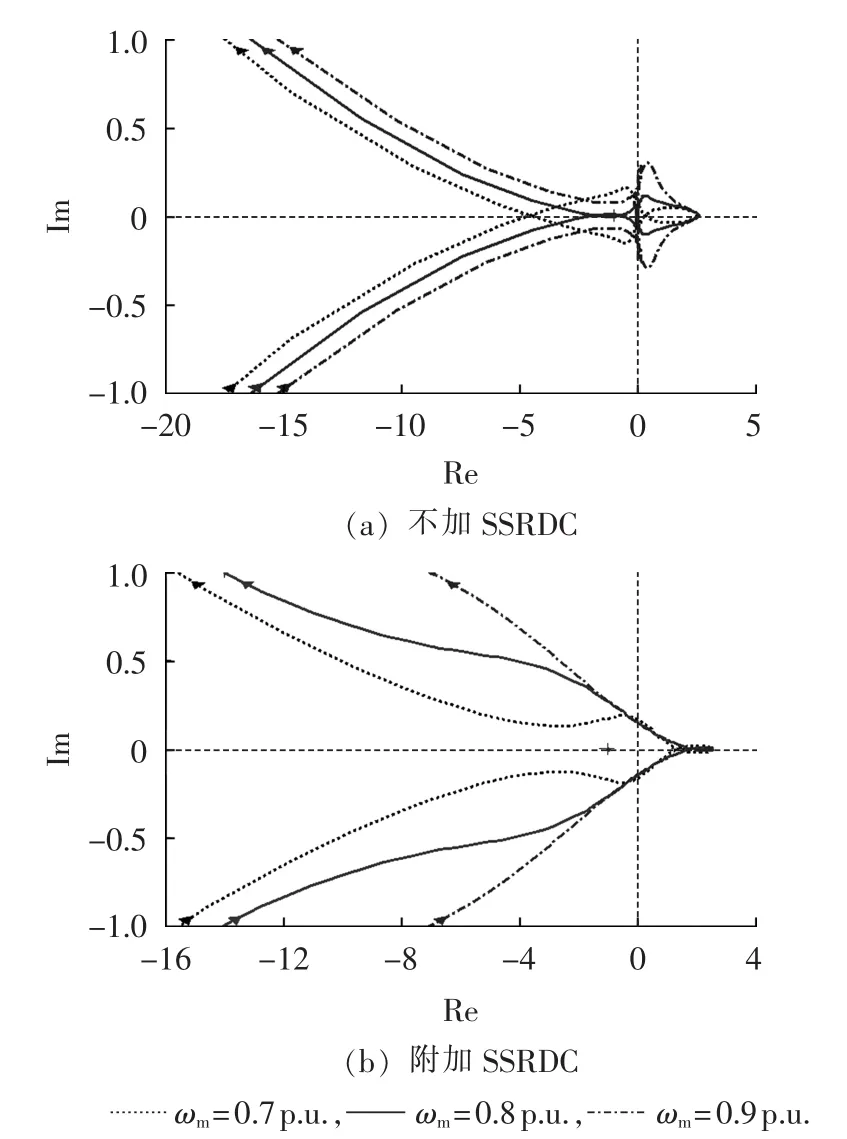
图16 不同风机转速下Znet/Zsr的奈奎斯特曲线Fig.16 Nyquist curves of Znet/Zsrfor different ωmvalues

4 仿真分析

在MATLAB/Simulink下搭建如图3所示的仿真系统，风机额定功率1.5 MW，定子额定电压575 V，定子电阻rs=0.023 p.u.，转子电阻rr=0.016 p.u.，定子漏感Lls=0.18 p.u.，转子漏感Llr=0.16 p.u.，励磁电感LM=2.9 p.u.。线路电阻RL=0.02 p.u.，线路电抗XL=0.5 p.u.。GSC侧滤波电抗XTg=0.3 p.u.。

4.1 转子侧附加SSRDC抑制SSR效果分析

设置2个仿真场景来检验SSRDC抑制SSR的效果：固定 ωm=1 p.u.，不同 δSC；固定 δSC=50%，不同ωm。 仿真结果如图17、18所示（Te为标幺值，后同）。

如图17所示，线路串补度越大，系统的SSR越严重。当δSC=50%时，系统最终的振荡会趋于稳定；当δSC=60%时，振荡加剧，此时的SSR谐振频率为25 Hz（振荡周期为 0.04 s）；当 δSC=70% 时，系统将失去稳定，此时的SSR谐振频率为33 Hz（振荡周期为0.03 s）。当附加SSRDC后，即使在δSC=70%时，系统的SSR都能被抑制，因此该附加控制器能够很好地抑制系统的SSR。如图18所示，风机转速越低，系统的SSR越严重。而附加SSRDC后，ωm变化时，SSR都能够被很好地抑制。2种情况说明，无论在高串补度，还是在低风速下，该控制都能够有效地抑制SSR。

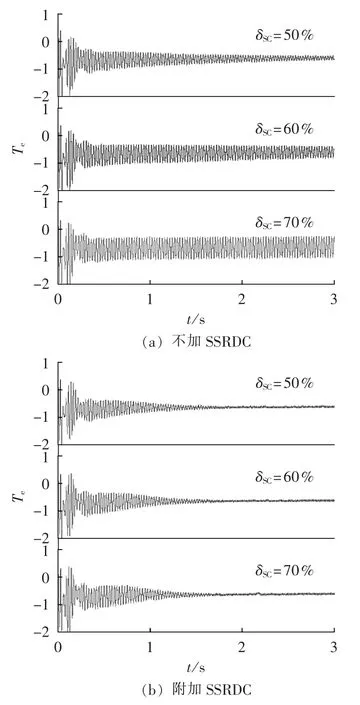
图17 不同串补度下SSRDC抑制SSR的效果Fig.17 Results of damping SSR with SSRDC for different δSCvalues

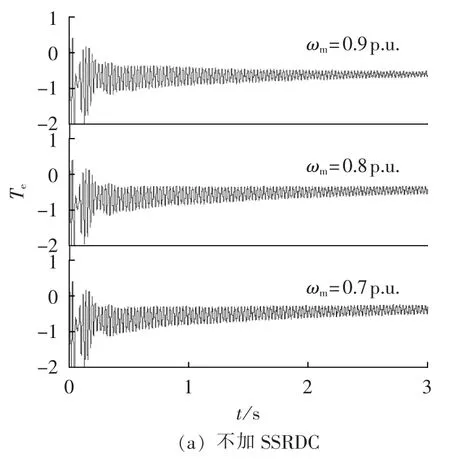
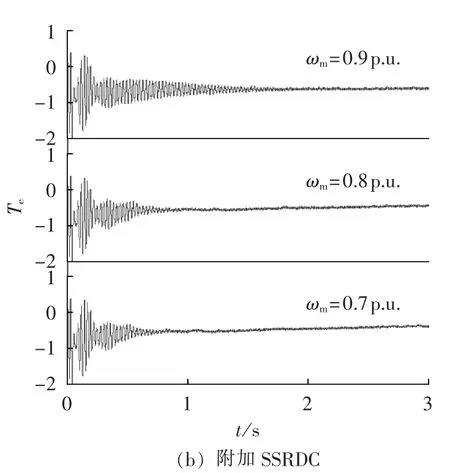
图18 不同风机转速下SSRDC抑制SSR的效果Fig.18 Results of damping SSR for different ωmvalues

4.2 转子侧和网侧附加SSRDC抑制SSR效果对比

如图19所示，当系统出现严重的SSR（δSC=70%或者ωm=0.7 p.u.）时，在转子侧附加SSRDC时，最终达到稳定所需要的时间明显少于在网侧附加SSRDC，因此可知，在转子侧附加SSRDC抑制SSR的效果优于在网侧附加SSRDC。

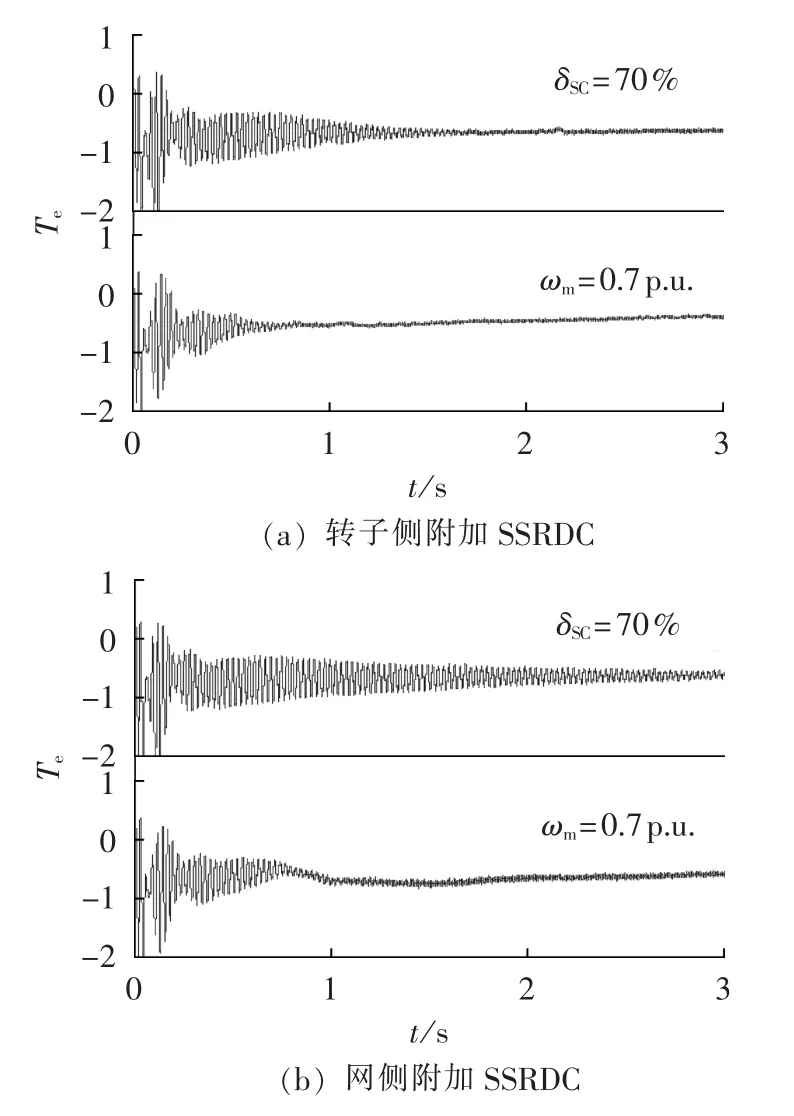
图19 转子侧和网侧附加SSRDC抑制SSR的效果Fig.19 SSR damping results of rotor-side and grid-side SSRDCs

4.3 基于阻抗法与基于状态空间法附加SSRDC抑制SSR效果对比

基于状态空间法设计的附加SSRDC[17]，该附加SSRDC采用的结构与基于阻抗法设计的附加SSRDC结构一样。2种方法设计的附加SSRDC抑制SSR的效果如图20所示，可以看出，基于阻抗法设计的SSRDC抑制SSR所需要的时间更少，因此可知，基于阻抗法设计的附加SSRDC抑制SSR效果更好。

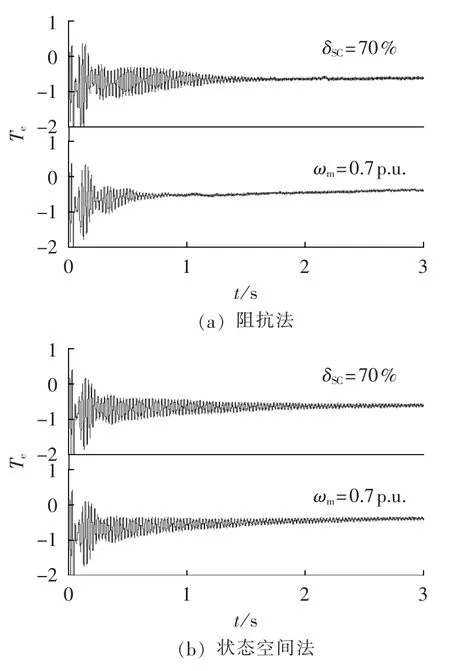
图20 基于不同方法设计SSRDC抑制SSR的效果Fig.20 SSR damping results of SSRDCs designed by different methods

5 结论

本文针对DFIG风机经串补线路接入网络造成的SSR，设计了相应的附加SSRDC；并且通过奈奎斯特稳定判据分析系统的稳定性，以此指导SSRDC参数的设计。最后，通过在MATLAB/Simulink中搭建仿真模型首先验证了该控制器能够有效地抑制SSR，其次验证了在转子侧附加SSRDC控制器比在网侧附加该控制器抑制SSR振荡的效果更好，最后验证了基于阻抗法设计的附加SSRDC抑制SSR的效果优于基于状态空间法设计的附加SSRDC。