一种新型同相牵引供电系统均流性能研究

何晓琼,彭 旭,周瑛英,王 远,舒泽亮,肖 建

（西南交通大学 电气工程学院,四川 成都 610031）

0 引言

牵引供电系统是电气化铁道的重要组成部分，承担着向电力机车提供能量的任务。目前，绝大多数国家均采用三相-两相分相供电模式，由于电气铁道接触网采用单相交流制，如果仅从电力系统单相取电将造成电力系统的不对称而使三相电压不平衡，因此现行牵引供电系统设置了电分相。由于电分相装置的存在，机车运行速度和承载能力受到限制，严重制约着高速重载铁路发展。为保证电力系统三相负荷对称性，提升机车运行速度和承载能力，世界各国对牵引供电模式开展了诸多研究[1-10]。

自文献[1]提出牵引网全线贯通供电以来，诸多学者对其系统架构展开了研究。本文研究一种基于三相-单相变换器的贯通式同相牵引供电系统[7]，该系统利用电力电子变流技术实现牵引网的贯通并网与柔性可控，可彻底取消牵引网电分相装置，能极大改善三相电网的电能质量。针对多个电压源模块的并网控制，最主流的控制方法有主从控制法和外特性下垂控制法[11]。本文研究的系统中各变电所之间不存在主从关系，因此，主从控制方法不适合于本系统。

本文建立了基于三相-单相变换器的贯通式同相牵引供电系统两变电所模型，分析了系统环流阻抗和下垂特性，设计了下垂控制策略，仿真验证了利用下垂控制进行变换器并网控制在该系统的可行性。

1 贯通式同相牵引供电系统结构

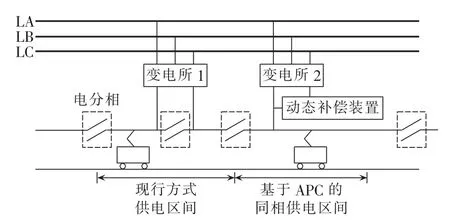
图1 现行分相供电系统与同相供电系统示意图Fig.1 Schematic diagram of present split-phase power supply system and co-phase power supply system

图1左半部分是现行牵引供电系统，变电所从三相电网向牵引网提供两相供电，为了保持系统功率平衡以及提高功率利用率，机车需要电分相。一方面，电分相会引起牵引网远端电压明显下降，所引起的谐波、无功以及三相不平衡电流会对电网产生巨大冲击；另一方面，电分相会使机车不能连续受流，造成机车速度以及牵引功率的巨大损失[12]。

基于既有线路改造的同相牵引供电系统已在四川眉山投入试运行，见图1右半部分。该系统通过Ynvd平衡变压器将三相变为两相。一相提供牵引功率，另一相连接动态补偿装置，为无功及单相负载电流谐波提供补偿，同时提供一半的有功功率。但是由于动态补偿装置连接到变压器次边的两相输出对于供电臂间的相位没有影响，因此系统难以实现贯通供电[13-14]。

图2 贯通式同相牵引供电系统模型Fig.2 Model of advanced co-phase traction power supply system

图3 三相-单相变换器结构Fig.3 Structure of three-phase to single-phase converter

基于三相-单相变换器的贯通式同相牵引供电系统如图2所示，三相-单相变换器结构如图3所示。该系统通过有源功率变换器实现功率在三相电网和牵引网之间直接传递，通过三相-单相变换器，可获得幅值/相位相等的单相交流电，并对无功、谐波进行补偿，同时平衡分配三相-单相系统的有功电流，机车可以在该系统任何位置受流。牵引网可以完全取消电分相，系统可以真正实现贯通供电，并能极大改善电能质量[7-8，13]。

2 牵引网阻抗计算

牵引网是牵引系统的重要组成部分，由接触网、铁轨及大地构成回路，贯通式同相牵引供电系统的接触网与现有铁路模型一致。因此，对该系统牵引网的分析可以参照现行牵引网阻抗分布分析进行。牵引网上工频电压频率较低，且占主导地位，但考虑动车在线路运行中产生的高次谐波问题，在牵引网阻抗的计算中，等效电容和电感的影响不可忽略。

根据图4牵引网电路最简模型[15]，图中z1为接触网-地回路自阻抗，z2为轨-地回路自阻抗，U为输出电压，U′为机车负载电压，可以得出回路电压方程如下：

则牵引网单位长度阻抗为：

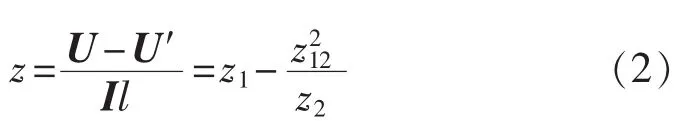
选取单线有加强全补偿链形悬挂，导线型号LJ-70+LGJ-185+GLCA-100/215，钢轨规格为50 kg/km。查阅相关参数[16]，计算得接触网-地回路自阻抗为0.136+j0.56Ω/km，轨-地回路自阻抗为0.198+j0.56 Ω/km，互阻抗为 0.05+j0.312 Ω/km，牵引网单位长度阻抗为0.14+j0.309 Ω/km。

3 系统环流分析

贯通式同相牵引供电系统虽然极大改善了电能质量，取消了电分相装置，却带来了新的问题。由于系统实现了贯通，各变电所并联运行，而各变电所参数及运行情况存在差异，因此变电所之间会出现环流。过大的环流不仅对负载没有贡献，反而会增加系统负担，甚至损坏设备，因此有必要对该系统的环流加以分析。

将变电所等效为电源，简化的两变电所并联回路如图 5 所示。 其中，U1，2是电源输出电压幅值；φ1，2是电源输出电压相位；Uo是负载电压幅值，其中负载相位在文中定义为 0°；X1，2是变电所等效输出感抗；R1，2是变电所等效输出电阻；Z′1，2是牵引网等效输出阻抗；ZL是负载，即运行的机车；I1，2是两电源输出电流。

图5 两变电所并联模型Fig.5 Model of two substations connected in parallel

为简化分析过程，假设 φ1=φ2，R1=R2，X1=X2，定义环流为IH，根据图5，有：

由于机车的运动造成Z′1，2的变化，设z′是牵引网单位长度等效输出阻抗，D是机车与左侧变电所距离，两变电所相距50 km，得：

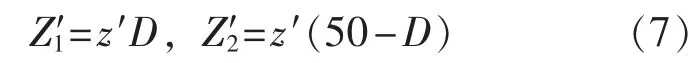
所以：

因此环流阻抗中的负载阻抗不能忽略，根据式（3）—（8），可得 I1，2及 IH的表达式分别为：

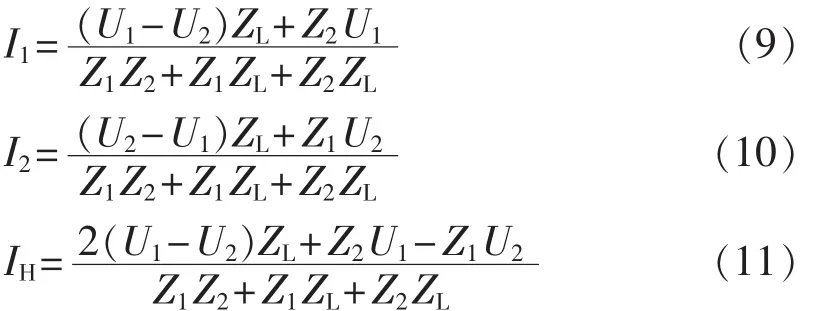
根据上述计算结果，取机车为恒阻抗模型[17]，ZL=62.5+j46.875 Ω。计算环流IH随距离D变化趋势如图6所示。

当D在[0，50]区间变化时，由图6可见：当D=25 km 时，图形出现拐点，此时，Z1=Z2=Z，式（11）可化简为：

图6 环流随D变化趋势Fig.6 Variation trend of circulation along with D

通过以上分析和图6可知，贯通式同相牵引供电系统多机并联运行时的环流不可忽略。

4 下垂特性分析及均流控制器设计

本系统多变电所并联运行等同于多个电源模块的并联运行，各模块由于参数不完全一致，使得其输出不同，有的甚至不输出，导致电流分配不均，引起环流，使部分模块开关应力过大，造成设备损坏，最终使系统可靠性降低。均流控制就是要采用合适的控制策略合理分配负载电流给各变电所，同时使输出电压符合系统要求，保证系统稳定工作。

4.1 系统下垂外特性分析

根据外特性下垂控制原理，下垂控制法的使用要求系统具有下垂外特性[11，18]。本系统与一般电力系统所不同的是负载在两电源之间运动，负载与两侧变电所之间阻抗动态变化，该系统是否具有下垂外特性，需要进行具体分析。

根据图5及式（3）—（8）计算可得该系统变电所输出功率如下：

其中，Rn为 Zn实部；Xn为 Zn虚部；n=1，2。

联立式（13）、（14）可得：

由第2节可知牵引网的阻抗通常较小，牵引网传输线对系统电压相位差影响较小，有sin φn≈φn、cos φn≈1。 因此，式（15）和（16）可简化为：

另外，牵引网阻抗中电抗数倍于电阻，因此变电所输出无功功率Qn对负载电压Uo与变电所电压Un的幅值差影响较大，变电所输出有功功率Pn对负载电压Uo与变电所电压Un的相角差φn影响较大。代入相关参数，可得贯通式同相牵引供电系统的有功与相角、无功与电压幅值变化量关系分别如图7、图8所示。可以看出，有功功率与相角的变化量、无功功率与输出电压幅值变化量近似成正比关系，当机车位置固定时，斜率基本为一负常数，且随着机车位置的移动，斜率始终为负，系统整体上具有下垂外特性。

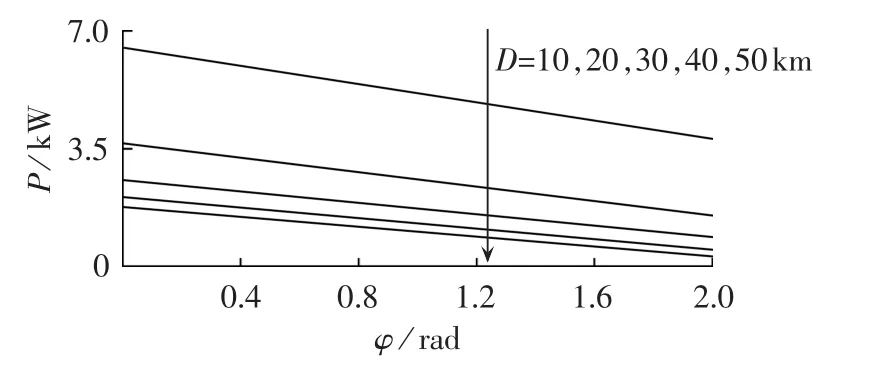
图7 P-φ曲线Fig.7 Curves of P-φ

4.2 均流控制器设计

根据前述系统下垂特性，建立图9所示的牵引网侧有功、无功的均流算法。该算法的前提条件是系统中各个变电所的电压频率与幅值无较大差异。而该前提条件在当前变电所接入的工业电网端口较易满足。

图9 下垂控制框图Fig.9 Block diagram of droop control

由式（13）和（14）推导出下垂控制公式如下[19]：

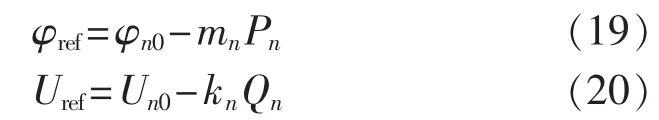
其中，φref、Uref分别为输出电压相位与幅值的参考值；φn0、Un0分别为变电所输出电压初始相位与初始幅值；kn、mn为下垂系数，主要与系统输出功率有关。由于两变电所间同一时刻一般只有一列机车，且机车运行基本不影响变电所输出功率，因此本系统的输出功率变化很小。综合考虑均流效果及动态响应，选kn、mn为固定值进行下垂控制设计。

通过检测变电所输出电压和电流，计算出Pn和Qn，根据各变电所有功与无功的变化，由式（19）和（20）得到给定电压相角和幅值，通过对输出电压的相角和幅值的控制，实现下垂控制，从而对环流进行有效抑制以达到均流效果。

5 仿真系统及仿真分析

5.1 仿真系统与仿真参数

贯通式同相牵引供电系统理论上可以由任意多个变电所组成。两变电所模型已可以研究该系统的绝大多数工况下的性能。因此根据下垂控制理论建立图10所示的两变电所仿真系统架构图。

图10 两变电所仿真系统Fig.10 Dual-substation simulation system

图10中变电所1和2为三相-单相变换器的贯通式同相牵引变电所，变电所由理想变压器、三相-单相变换器组成。系统电压设定为25 kV；模拟实际情况，设两变电所初始相位差为5.73°，初始幅值给定相差250 V；两变电所间设置模拟牵引负载，由于机车（特别是动车）运行时无功很小，根据牵引负荷功率推算，取负载为168 Ω；各变电所与负载之间的牵引网简化为T型等效电路，等效电阻0.2568Ω/km、电感0.002 H/km、电容8.6 nF/km；根据工程实际，设两变电所相距50 km。

模拟系统运行过程：0s时，变电所1投入运行，系统空载；0.2s时，变电所2投入，与变电所1并网运行，系统空载；1s时，负载在距离两变电所均为25 km处投入；5 s时，由于机车在此期间发生位移，负载两侧线路阻抗发生变化，负载位移设定为500 m；8 s时，负载离开，等效为被切除。

5.2 仿真结果及分析

图11是机车受流处电压Uo、变电所1输出电压U1与变电所2输出电压U2波形，两变电所设计为电压源模型，由图可知Uo有效值始终在牵引网规定的电压范围内变动。图12是负载电流、变电所1输出电流、变电所2输出电流以及上述两变电所之间的环流波形。由图12可知，在0.2 s前，只有变电所1空载，所以不存在环流问题；0.2 s时变电所2投入，虽然没有向牵引负载供电，但由于两变电所之间存在初始值的差异，造成瞬时的环流很大，达到50 A左右，由于系统加入了下垂控制，环流迅速被抑制在2 A左右；在1 s时，两变电所电流相位、幅值已基本被调整一致，此时投入牵引负载，两变电所间已基本不存在环流，阻性牵引阻抗使得输出电流幅值在2～8s几乎保持不变；5 s时，机车移动500 m引起系统阻抗值的变化，从而产生环流，然而环流较小，仅17 A，并且也很快被抑制在2 A左右。可见变换器能够根据负载与线路阻抗自动分配电流大小，系统可以实现均流。

图11 负载、变电所1和2的输出电压波形Fig.11 Voltage waveforms of load，substation No.1 and No.2

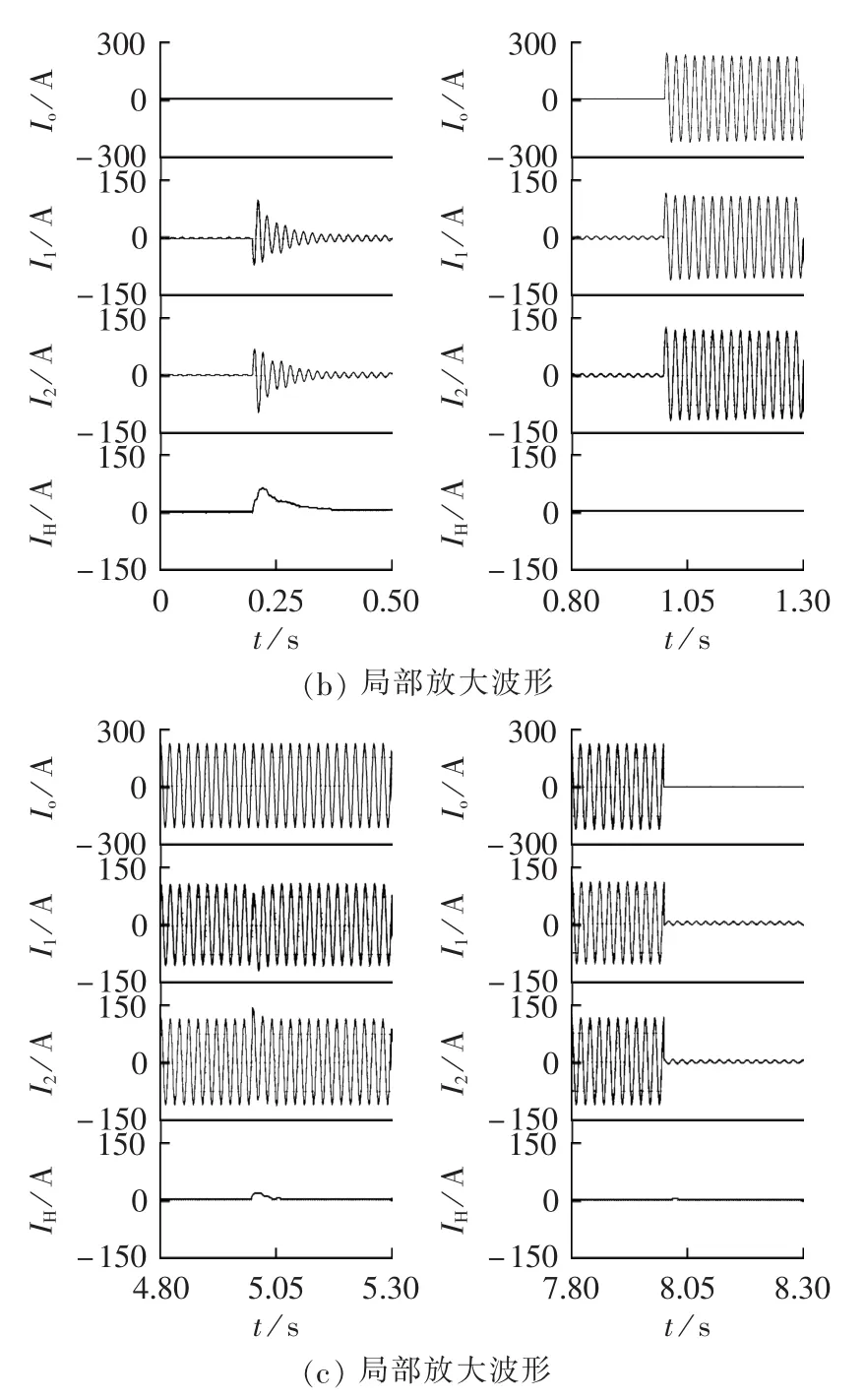
图12 负载、变电所1和2的电流与系统环流波形Fig.12 Current waveforms of load，substation No.1&No.2 and circulation

6 结论

本文针对现行牵引供电系统存在的缺陷，研究了一种基于三相-单相变换器的贯通式同相牵引供电系统，分析了系统阻抗、环流和下垂特性，讨论了均流控制方法，计算得出了系统牵引阻抗，得到该系统环流分布特性，得出该系统具有下垂外特性，并设计了下垂控制策略。本文利用MATLAB/Simulink建立了两变电所贯通式同相牵引供电系统模型，通过仿真验证了该系统可根据负载和线路阻抗分布特征，通过下垂控制使系统实现均流。