电力系统暂态稳定性闭环控制（五）——控制量的实时计算

张保会，王怀远，杨松浩，马世英

（1.西安交通大学 电气工程学院，陕西 西安 710049；2.中国电力科学研究院，北京 100192）

0 引言

在电力系统遭受大扰动[1-5]快速判别出暂态不稳定后，立即正确算出需要的控制量[6-11]，是保证控制有效性和经济性[12-13]的重要环节。文献[6]论述了离线和实时准确计算最小切机量的理论和实际困难，本文将探讨切机量近似计算的原理[14]与方法。

文献[1]提出了基于相平面轨迹凹凸性变化的暂态不稳定性判别理论，文献[2]经过增加判别轨迹穿越拐点时变化率方向场的符号，将该理论推广至多机系统并做了相应的验证。分析轨迹的凹凸性特征及角速度与功角的关系，不稳定的系统轨迹在其通过动态鞍点（DSP）[15]时，对应的角速度不为0，系统不会回摆。而稳定的轨迹在其达到动态鞍点前其角速度一定会存在为0的时刻（对应最大摇摆角），并且发生回摆。本文的学术思想就是通过切机措施使得不稳定的系统轨迹在其动态鞍点处（或前）的角速度降为0，系统开始回摆。

通过控制改变轨迹的发展使其由不稳定变得稳定，需要进一步研究控制量与轨迹发展的关系，本文首先研究相轨迹斜率的变化趋势与轨迹凹凸性变化的关系，进而研究相轨迹斜率与控制量的关系，解决基于实测的轨迹信息最小控制量的实时近似计算问题。而最小控制量与允许的系统最大摇摆角有关，本文提出2种方法：第1种方法是给定一个最大摇摆角，通过切机控制使得系统轨迹在给定的最大摇摆角处返回，系统保持稳定，所给的系统的最大摇摆角必须小于不稳定平衡点角度，否则计算出的控制量无法使系统恢复稳定，其优点是最大摇摆角可控，可根据更复杂的控制要求调整；第2种方法是假设切机控制前后两区域间电磁功率曲线未发生变化或者变化幅度很小，最大摇摆角自动计算，保持暂态稳定。实际电网的规模非常大，等值为两群系统后切除少量机组对于两群间电磁传输曲线的影响较小，不稳定平衡点的变化对于切机量的影响可以忽略不计，可以做到完全自动计算。在单机无穷大系统和三华联网系统进行了仿真，验证了本文算法的有效性。

1 相轨迹斜率的时间特性与稳定性关系分析

回顾文献[1]用相轨迹几何特征判别暂态不稳定的有关判据，相轨迹斜率为：

相轨迹拐点为：

不稳定判据为：

其离散表达式为：

其中，Δω（i）、δ（i）分别为系统的角速度偏差、角度。 在Δω-δ相平面内，当τ（i）＜0 时，相轨迹相对于稳定平衡点的几何特征是凹的，系统稳定；若某时刻τ（t）＞0，相平面轨迹从凹区域穿入凸区域，系统将失去稳定[5]。

对于图1所示系统，在其输电线路L2上发生短路，0.25 s跳开故障线路切除故障，系统临界稳定，0.3 s跳开故障线路，系统不稳定。对于不稳定的故障，在0.43 s时完成切除不同比例的机组，切除机组容量不足时，系统依然失稳，对应的角速度偏差、相轨迹斜率曲线如图2所示，图中角速度偏差为标幺值。

图1 单机无穷大系统示意图Fig.1 Schematic diagram of a SMIB system

图2 不同切机量的相轨迹斜率Fig.2 Slope of phase trajectory for different control quantities

考察相轨迹斜率k（t）随时间的变化方向，对于稳定的轨迹，其变化率持续减小并在最大摇摆角处发生符号跃变，因为在最大摇摆角处角度随时间变化率为0，而角速度偏差随时间变化率改变符号，轨迹不会到达拐点，轨迹回摆，系统不会失稳。对于不稳定的轨迹，其变化率并非持续减小，在拐点处开始增大并在功率平衡点处开始大于0。对于经切机控制后的轨迹，切机使得相轨迹斜率突然减小，切机量越大斜率减小越多。如果切机量不足，在轨迹拐点处斜率开始增大并在功率平衡点处开始大于0，系统仍然失稳；如果切机量足够，相轨迹斜率持续变小，在最大摇摆角处发生符号跃变，轨迹不会到达拐点，轨迹回摆，系统经切机控制后稳定；对于使得系统稳定的最小切机量控制后的轨迹，相轨迹斜率持续变小，并在功率平衡点处发生符号跃变，轨迹回摆，系统经切机控制后临界稳定。

定理3：在功率平衡点前，欲使相轨迹由凸区域向凹区域运动且不再回到凸区域，则相轨迹斜率持续变小。

等价于文献[1，4]所提定理1，相轨迹一直运行在凹区域内，不再回到凸区域，系统稳定，故定理3得证。

2 切机控制量的计算

对于稳定的系统，角速度偏差在最大摇摆角处为0，相轨迹在该点开始回摆；而不稳定的系统，角速度偏差在功率平衡点处达到最小，但不为0，经过不稳定平衡点之后，角速度偏差继续增大，从而失稳。对于将要失稳的系统，通过切机控制使得系统在指定的最大摇摆角或功率平衡点处角速度偏差为0，才能恢复稳定，以此为控制目标计算所需切机控制量。

对其相轨迹斜率进行积分，取积分下限为切机时刻的功角δa，积分上限为功角δb，可以得到：

式（6）表达了相轨迹斜率与角速度偏差间的关系，对于稳定的系统，当δb对应于系统的最大摇摆角时，对应的角速度偏差Δωb为0时，相应为式（6）的第一项为 0。 再次回顾式（1），k（t）表达了不平衡功率与角速度偏差的关系，如果能够求得稳定控制需要的k（t），进而可求得切机控制量。

观察图2中切机控制后的k（t），它是非线性变化的，切机量越大，k（t）向负方向变化率越大，对应不同的最大摇摆角处角速度偏差为0，需要的切机量不同。当在功率平衡点处角速度偏差为0时，对应一个临界最小切机量，则该切机量就是使得系统由不稳定变稳定需要的最小切机量，记为：

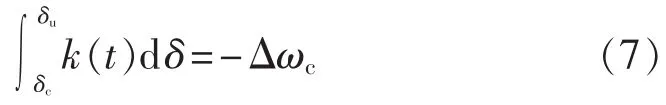
其中，δc为切机时刻系统的功角；δu为系统的不稳定平衡点功角。

若能得知最小切机量在切机时刻对应的相轨迹斜率，通过式（1）就能求得系统所需要的最小切机量。 由于 k（t）非线性变化，且 k（t）值的求取显然与计算需要的切机量构成了一个“环锁”问题[7]，因此需要近似计算。假定切机控制后至最大摇摆角前，相轨迹斜率是常数，采用一个恒定不变的k′值来代替式（7）中 k（t），可以得到：

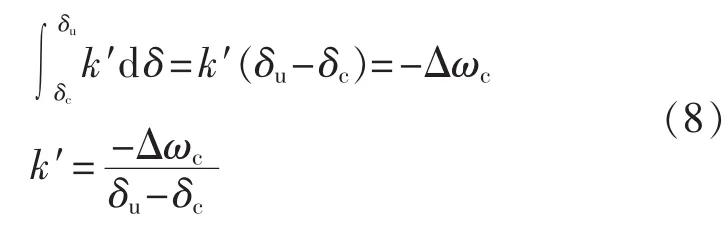
显然欲求得k′，需要知道切机时刻的角度与角速度偏差，可通过实时测量得到；最大摇摆角可以给定或见第3节求取方法。采用该近似方法得到的k′要略小于最小切机量对应的切机时刻的相轨迹斜率，因此通过k′求取的切机量要略大于最小切机量，结果偏保守。

对于单机系统，可以假定切机比例为λ，切除出力的同时也减小了惯性，回顾式（1），切机后k′与切机量λ的对应关系为：

将式（8）代入式（9）并变换得到：

其中，Pec为电磁功率在切机时刻Tc的值；Δωc为角速度偏差在切机时刻Tc的值。当已知k′时，用式（10）可得切机量。

对于实际的多机系统，按照文献[2]的方法将其等值为超前群S与滞后群A两群，进而等值成单机系统。为快速求取切机量，近似认为切机后系统的惯量未发生变化，可以得到式（11）计算超前群S所需要的切机量：

其中，Pms和Pes分别为超前群S在切机时刻的等值机械功率和电磁功率；Pma和Pea分别为滞后群A在切机时刻的等值机械功率和电磁功率；M为系统所有机组的总惯量；MT为等值单机系统的惯量；Ms和Ma分别为超前群S和滞后群A的总惯量；Δω为等值单机系统在切机时刻的角速度偏差。

3 最大摇摆角的求取

控制量计算的表达式中，其他的变量均可以通过WAMS得到，而切机后的最大摇摆角需要通过给定或自动计算事先获得，采用2种方法得到系统的最大摇摆角。

方法1：最大摇摆角定在切机后系统的功率平衡点（也称不稳定平衡点），进行自动计算。对于实际的多机电力系统，等值单机无穷大系统的电磁传输功率可用时变的功角函数表达，如式（12）所示，机械输入功率在短时间内认为不变。当执行切机操作时，认为电磁功率没有发生变化，而机械功率按切机量相应地减少。

其中，Pc（t）、λ1（t）、λ2（t）为待辨识的时变参数。 就某一确定时刻的系统运行状态而言，只要等值输电断面中不发生大的网络操作，参数在短时间内可当成定常不变，即只需要利用判出不稳定时刻前的等值实测功率差，利用最小二乘法辨识一次参数，确定出电磁传输功率。

对于切机后的功率平衡点的求取，需要已知切机量，因此可以通过迭代的方法求取。迭代的步骤如下：

a.完成电磁传输功率的预测；

b.初始迭代时，给定切机量为0；

c.机械输入功率根据切机量而相应地减小；

d.找到电磁功率和机械功率相等时对应的功角，即为不稳定平衡点 δu（n）；

e.通过不稳定平衡点返回计算切机量 ΔP（mn）；

方法2：限定系统的最大摇摆角。根据实际系统的运行控制需要，给定系统允许的最大摇摆角。所选取的最大摇摆角必须在系统的不稳定平衡点之内，否则计算出的控制量无法使系统恢复稳定。

4 仿真验证

4.1 单机无穷大系统下的仿真

在PSASP仿真软件中搭建如图1所示的单机无穷大系统。发电机采用E′恒定模型，初始条件如下：惯性常数取19.6 s，不考虑调速调压器作用，正常运行在功角46.5°。故障条件为t=0在L2线路首端发生三相短路，在不同的时间切除L2线路。用文献[2]的判据以不同的时间判出不稳定，假定延迟50 ms完成切机，本文算出的最小切机量与仿真试凑得到的最小切机量比较见表1，自动计算获得的最小切机量比仿真得到的略多，确保了切机后系统稳定。

与表1的故障条件、判别方法相同，表2是限定系统的最大摇摆角180°计算所需的最小切机量。可以看出：按照该算法所得的切机量进行切机控制，切机后的最大摇摆角与所限定的值非常接近，并且不会超过限定的摇摆角，保证在控制目标内。

表1 自动计算最小切机量准确性校验Table 1 Accuracy verification of automatically-calculated minimum control quantity

表2 限定最大摇摆角得到的切机量Table 2 Control quantity calculated with restraint of maximum swing angle

4.2 三华联网系统暂态稳定控制仿真

参见文献[2]给出的不稳定判别方法及三华联网系统。故障场景为0 s洪沟—板桥线路发生三相短路接地故障，0.1 s保护装置动作跳开线路，故障清除。保护装置动作之后的功角曲线如图3所示，系统依然失稳。

图3 洪沟—板桥三相接地故障0.1 s切除后的功角曲线Fig.3 Power-angle curves after Honggou-Banqiao three-phase grounding fault is removed at 0.1s

利用文献[2]给出的不稳定判别方法，在0.94 s判别出系统不稳定，此时启动控制量计算。认为系统的不稳定平衡点未发生变化，通过拟合系统的不平衡功率自动获得不稳定平衡点，计算得到控制量为切除4568 MW的机组，延迟300 ms后完成切机，图4给出功角摇摆曲线，合适的切机控制后系统稳定。

给定一个等值系统的最大摇摆角为180°、本文计算得到的控制量为切除6992 MW的机组，切机完成之后的功角曲线如图5所示，等值系统的最大摇摆角为177.5°，在限定的系统最大摇摆角内。

图4 切除4568 MW机组后的功角曲线Fig.4 Power-angle curves after 4568 MW unit is tripped

图5 切除6992 MW机组后的功角曲线Fig.5 Power-angle curves after 6992 MW unit is tripped

5 结论

电力系统中不稳定的相轨迹其斜率通过拐点后随角度逐步变大，欲使不稳定的轨迹向稳定的轨迹变化，施加的控制需要满足轨迹的斜率在功率平衡点前持续变小。在多机系统中可以认为切机控制后系统的不稳定平衡点没有发生变化，利用控制前的功率差拟合来确定控制后的不稳定平衡点，自动计算切机控制量；也可以给定一个系统最大摇摆角，计算切机控制量。

仿真结果表明，控制执行后的系统能够不再失稳，本文的成果解决了控制量实时计算的难题。