基于贝塔分布的风电功率波动区间估计

刘兴杰，谢春雨

（华北电力大学 电力工程系，河北 保定 071003）

0 引言

近年来，随着《风电开发建设管理暂行办法》等相关法律法规的不断完善，我国的风电得到了快速的发展。2012年，中国（不包括台湾地区）累计安装风电机组53764台，装机容量75324.2 MW，同比增长20.8%[1]。随着风电大规模的并网，风电本身具有的波动性、间歇性和随机性不但会导致互联系统的潮流发生改变，给系统造成反调峰[2]，增加额外的备用电源，同时也会影响风电穿透功率极限[3]，进而影响风电行业自身的发展。精确的风电功率预测是解决上述问题的好办法。然而，目前确定性风电功率点预测依然存在着较大误差，且其预测结果无法反映风电功率波动特性。相比之下，波动区间预测则包含更多的信息，有利于决策者更好地认识未来变化可能存在的不确定性和面临的风险[4]，因此有必要对风电功率预测误差分布规律进行研究和对未来风电功率波动区间进行预测。

目前国内对风电功率波动区间预测的相关研究还比较少。文献[5]利用神经网络对风电预测误差带进行了计算，得出误差基本上符合正态分布。文献[6]在正态分布模型的基础上，根据概率密度函数以及最小二乘法的相关理论提出了一种描述预测误差的正态优化分布模型。文献[7]采用非参数核密度估计方法求取功率预测误差分布的概率密度函数并计算了功率预测的置信区间。文献[8]提出了一种基于分位点回归的理论，对风电功率波动区间进行了预测。国外对风电功率不确定性研究比较早。文献[9-10]分别利用柯西函数和高斯函数对风电功率预测误差分布进行了拟合。文献[11]利用核密度估计技术，得到完整的预测概率密度函数，用于预测风电短期预报。文献[12]利用粒子机和贝叶斯估计，以GP模型建立预测模型，用于风电功率预测。文献[13]采用ANN得到不确定方法，将相关置信水平下的不确定性信息应用至电网调度，并采用Chebyshev不等式对短期风电功率预测误差分布进行了研究。文献[14]在机组优化组合研究中，利用正态分布对风电功率预测误差进行建模分析。文献[15]在对预测功率分区间讨论的基础上，利用标准贝塔分布对归一化后的风电实测出力波动规律进行了研究，但并未对功率预测误差频率分布进行分析，且标准贝塔分布的自变量取值范围有一定的局限性，不适合对风电功率预测误差分布进行拟合。本文通过分析发现风电功率预测误差概率分布并非完全对称的正态分布，而成偏态分布，且风电功率预测误差频数分布随预测功率水平的变化而呈现不同的波动性，所以如果缺乏对预测误差频率分布的偏态性和随功率预测水平的变化而呈现不同波动性的考虑，则会对拟合结果的精度产生较大影响。

基于此，本文在风电预测功率区间合理划分的基础上，利用参数优化后的非标准贝塔分布对功率预测误差频率分布进行拟合，进而对风电功率的波动区间进行了估计，便于系统运行人员更好地认识未来可能存在的不确定性，做出合理决策。最后以内蒙古某风电场的历史数据为例对该优化模型的有效性进行了验证。

1 风电功率预测误差概率分布特性分析

1.1 风电功率预测误差

本文以内蒙古某风电场2012年5—8月份实际数据和基于神经网络功率预测方法所得到的未来10min的预测数据为例进行预测误差分析。实际运行中风电机组实际出力值和预测值并不完全相符，且该不相符由于风电出力预测模型精度、风电场地理环境[16]、风电功率预测时间间隔[17]等因素不同而呈现预测值大于、小于或者滞后于实际值的程度不同。图1为内蒙古某风电场5月1日风电实测功率和未来10min的预测功率，从图中可以看出实测功率和预测功率并不完全相符。

图1 风电预测功率和实测功率Fig.1 Forecasted and measured wind power

本文为便于对功率预测误差进行分析，对实测功率和预测功率进行了归一化处理，即：

其中，Pm为风电场实际功率；Pp为风电场预测功率；PN为风电场额定功率，该内蒙古风电场额定功率为99 MW；P′m为归一化后风电场实际功率；P′p为归一化后风电场预测功率。取预测误差d为：

1.2 预测功率区间分段

为了更细化研究预测误差的分布特性，本文在MATLAB环境下，利用内蒙古某风电场2012年5—7月风电历史数据，得出了不同预测功率区段下的预测误差频数分布，如图2所示，图中预测误差为标幺值，后同。

图2 预测误差频数分布Fig.2 Frequency distribution of forecast error

从图中可以看出，不同预测功率区段下预测误差的波动情况差别很大，当预测功率较小时，预测误差频数分布相对集中，而随着预测功率的增大预测误差频数分布越来越分散。

预测功率区间越细化，越能体现误差分布规律，但当数据总体量一定时，预测功率区间越细化，各样本的数据量就越少，使得某些区间样本数量不足以较好地反映出预测误差统计规律。结合参考文献[19-20]的研究结果，本文将功率预测分为[0，0.1PN）、[0.1PN，0.2PN）、[0.2PN，0.4PN）、[0.4PN，PN]4 个区段进行探究。

1.3 预测误差概率分布的偏态性

预测误差虽不可避免，但依然可以建立相关的数学模型对其规律进行拟合分析，如文献[5-6，14]都对预测误差采取正态分布模型进行拟合。图3为在MATLAB环境中所做4个预测功率区段上的预测误差样本数据的正态概率图，图中曲线①—④和曲线⑤—⑧分别表示样本数据1—4和正态分布数据1—4。从图中可以发现，所得4个区间预测误差样本数据和正态分布数据并不完全重合（如果样本数据分布符合正态分布，则样本数据应与正态分布数据重合且显示为直线），由此可见风电功率预测误差并不完全服从正态分布，而是呈现不同程度的正偏或负偏分布，所以如果所建模型能够充分考虑这种偏态分布，则风电功率预测区间估计的精度会进一步提高。

图3 风电功率预测误差正态概率图Fig.3 Normal probability of wind power forecast error

2 贝塔分布

基于第1节功率预测误差概率分布特性分析，同时由于标准正态分布自变量取值范围为[0，1]，不适合对取值范围为[-1，1]的风电功率预测误差进行拟合，所以本文选择非标准贝塔分布对风电功率预测误差概率分布进行拟合。

2.1 非标准贝塔分布密度函数

设随机变量的密度函数为：

其中，μx和σx分别为x的均值和标准差。

2.2 贝塔分布的优点

贝塔分布密度函数的优点如下：

a.函数简单，只有2个参数γ、η；

b.贝塔分布密度函数形状由参数γ、η来控制，即只要选择适当的γ和η，贝塔分布可以对多种不同形状的频率分布图形进行拟合，体现出良好的适应性和普适性；

c.贝塔分布密度函数是一个有界函数，上、下界分别为 a、b。

3 模型优化

3.1 模型参数优化

由第2节分析可知，贝塔分布的位置和形状由上、下边界a、b和形状参数γ、η确定，为进一步提高贝塔分布的拟合精度，本文通过迭代法对其上下边界值和形状参数进行了优化，步骤如下。

a.设预测误差样本数据为 di（i=1，2，…，n），计算预测误差样本均值d和方差S2d。

b.对预测误差样本 di排序，令 y1=dmin，yn=dmax，y1≤y2≤…≤yn，其中dmin和dmax分别为样本数据的最小值和最大值。

c.计算上、下边界a和b的初始值：

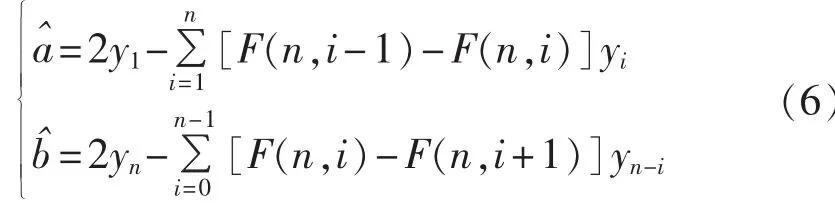
其中，F（n，i）=（1-i/n）n。

d.计算形状参数γ、η的初始值：

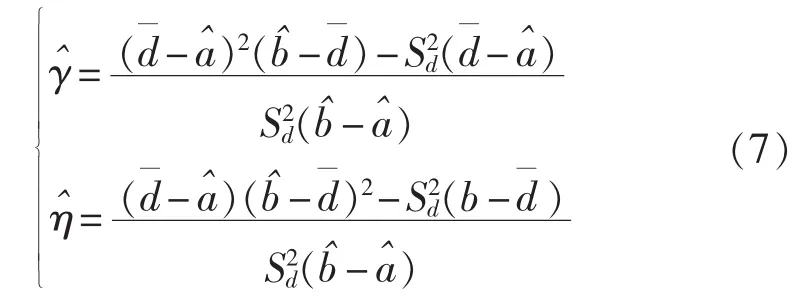
计算边界b的新估计值：

f.计算边界a的新估计值：

其中，Acc为预定精度，本文取0.0000001。

3.2 置信区间的求取

由第3.1节迭代结束后所得贝塔分布函数自变量新的上下边界和形态参数估计值可得参数优化后的预测误差概率密度函数，对其进行积分从而得分布函数F（di）。

本文采用估计区间最狭原则求得对应置信水平下的置信区间，即：

其中，1-a为对应置信水平。

4 实例分析

4.1 预测误差概率分布拟合和波动区间估计

为验证所建模型的有效性，本文引用正态分布模型和参数优化前的贝塔分布模型进行对比分析。在MATLAB环境下，利用参数优化后的贝塔分布模型进行拟合，当预测功率区段为[0，0.1PN）时，经过4次迭代后，求得优化贝塔分布相关参数分别为，同时利用正态分布模型和参数优化前的贝塔分布模型对预测误差概率分布进行拟合，结果如图4所示。同理可以依次求得其他区段的拟合曲线，图5为[0.1PN，0.2PN）区段功率预测误差拟合曲线。

根据参数优化贝塔分布模型所得各区段概率密度函数，对2012年8月1日前139个时段，依据第3.2节公式对置信水平为90%的风电功率波动区间进行估计，结果如图6所示。

同时，分别利用正态分布和参数优化前贝塔分布模型，对置信水平为90%的风电功率波动区间进行估计，结果如图7和图8所示。

图4 [0，0.1PN）区段功率预测误差拟合曲线Fig.4 Fitting curves of forecast error for power segment[0，0.1PN）

图5 [0.1PN，0.2PN）区段功率预测误差拟合曲线Fig.5 Fitting curves of forecast error for power segment[0.1PN，0.2PN）

图6 90%置信水平下优化贝塔分布功率波动区间Fig.6 Power interval estimated with optimized beta distribution model at confidence level of 90%

图7 90%置信水平下正态分布功率波动区间Fig.7 Power interval estimated with normal distribution model at confidence level of 90%

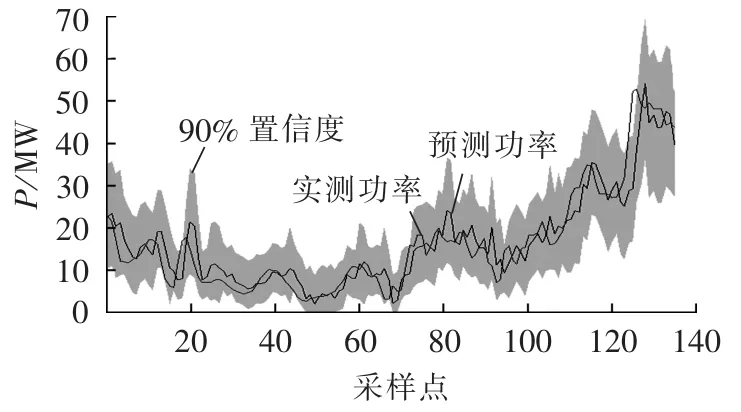
图8 90%置信水平下贝塔分布功率波动区间Fig.8 Power interval estimated with beta distribution model at confidence level of 90%

4.2 模型结果对比

为分析优化贝塔分布模型的有效性，本文利用预测区间覆盖率PICP（Prediction Interval Coverage Probability）δPICP、平均带宽和分辨能力 σΔP系数对 3个模型的预测精度进行对比分析。

若第i个实际出力值位于对应置信水平下的预测置信区间内，则取ci=1，否则取ci=0。δPICP≥（1-a）%时模型是有效的，否则模型需要改进。

平均宽带反映了波动区间宽窄的具体情况，在同一置信水平下，平均宽带越小则说明所建模型越好。

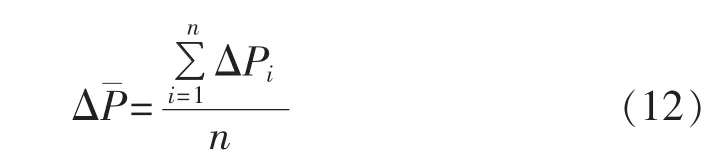
分辨能力系数能够对所建模型的所得误差情况进行分析，其值越大说明估计结果越好，其表达式如式（13）所示：

经过计算，在置信水平均为90%情况下，各指标结果如表1所示。

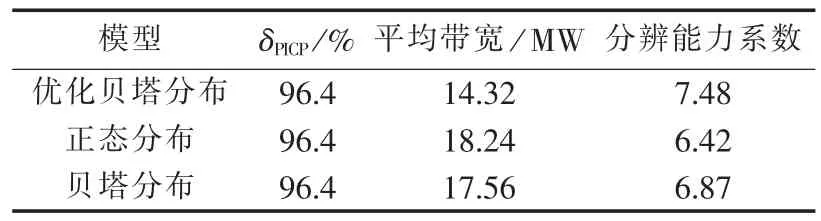
表1 模型指标对比结果Table 1 Comparison of indexes among different models

从表1可知，在置信区间相同的情况下，3个模型的预测区间覆盖率相同，而优化贝塔分布模型的平均带宽要小于正态分布和贝塔分布模型，同时优化贝塔分布模型的分辨能力系数要高于其他2个模型。可见参数优化贝塔分布模型要优于正态分布和贝塔分布模型。但从图中也可以看出，优化贝塔分布和另外2个模型在处理拐点处的波动区间估计效果并不理想，仍需对模型做进一步改进。

5 结论

在电力系统运行中，面对风电功率较强的波动性和间歇性问题，更好地把握风电功率的波动规律能够为运行人员的决策提供有效的依据。本文结合功率预测区间分段方法，利用参数优化后的非标准贝塔分布对风电功率预测误差概率分布进行了拟合，并利用所得分布函数对风电功率预测的波动区间进行了估计。通过对功率预测误差分布特性分析和实例验证可以得出以下结论：

a.不同风电预测功率区段下，功率预测误差概率分布拟合曲线不同；

b.本文所建立的模型考虑了风电功率预测误差概率分布的偏态性，相较于正态分布模型能更好地拟合预测误差概率分布，得到与实际分布一致的拟合函数；

c.通过对内蒙古某风电场算例分析，相对于正态分布模型及未优化贝塔分布模型，本文所建优化贝塔分布模型能够更有效地提供风电功率波动区间分析结果，这对电网经济运行以及提高风电场预测精度具有积极意义。