大数定律和中心极限定理在极限问题中的应用

罗逸平

（湖南城市学院 数学与计算科学学院，湖南 益阳 413000）

大数定律和中心极限定理是概率论的重要内容.大数定律给出了在试验次数很大时频率和平均值的稳定性，从理论上肯定了用算术平均值代替均值，用频率代替概率的合理性.中心极限定理阐明了在什么条件下，原来不属于正态分布的一些随机变量其总和分布渐近地服从正态分布，为我们利用正态分布来解决这类随机变量的问题提供了理论依据.它们都是通过极限理论来研究概率问题.反过来，本文研究了利用大数定律和中心极限定理处理极限问题的常用方法.

1 利用大数定律处理极限问题

证明 设{ξk}相互独立同分布，ξk～b(1,x),k=1,2,….令 ξn=，则由二项分布的再生性，ξn～B(n,x).所以

因为 f(x)在(0,1)连续，所以对坌x∈(0,1)及 ε>0，埚δ>0，当y∈(0,1):|y-x|<δ 时，恒有.因为 f(x)在(0,1)有界，设.由全数学望公式，有

由辛钦大数定律，有

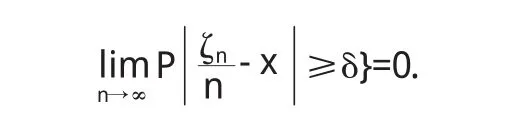
故对上述 x∈(0,1)及 ε>0，埚N∈N，对埚n>N，有

证毕.

类似地，

（1）利用Poisson分布的再生性和大数定律，可得

（2）利用几何分布的再生性和大数定律，可得

若 f(x)在[1,+∞)有界连续，且

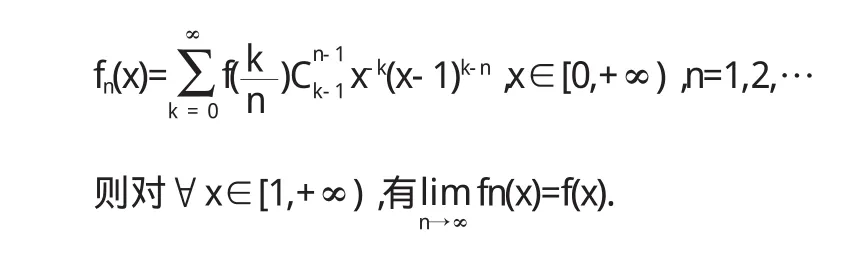
结合已知条件的特点，巧妙构造一类随机变量序列，利用大数定律是解决这类问题的关键.

2 利用中心极限定理处理极限问题

例2

证明 设随机变量序列{ξk}相互独立同分布，ξk～Γ(α,β)，即ξk的密度函数为

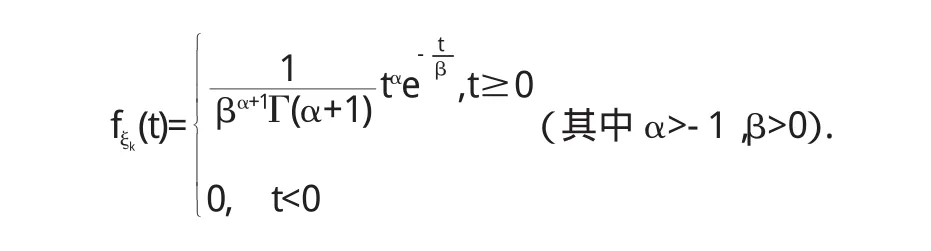
由Γ－分布的可加性，有

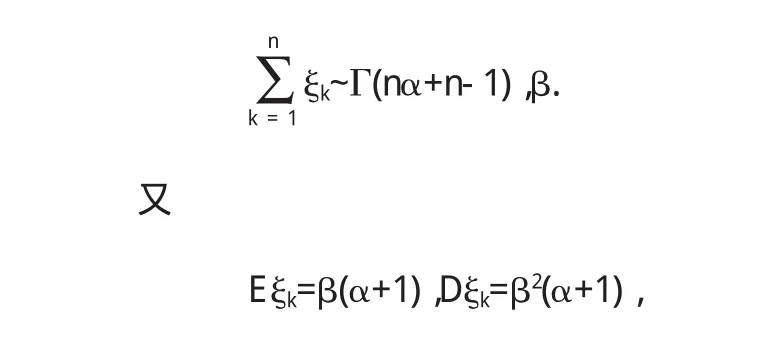
且

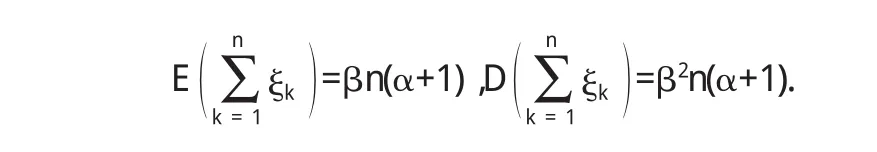
由Lindeberg-Levy定理，

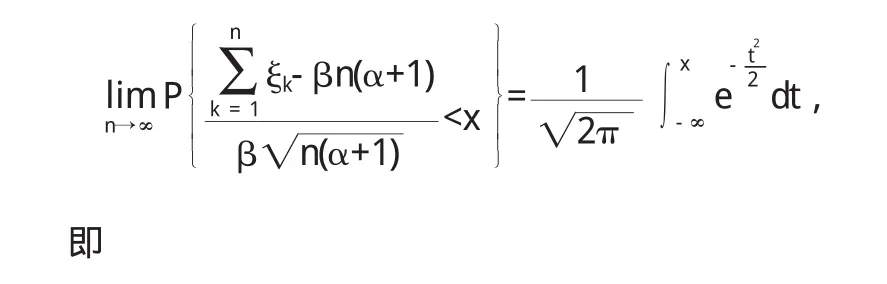
对坌x∈R，当n充分大时，

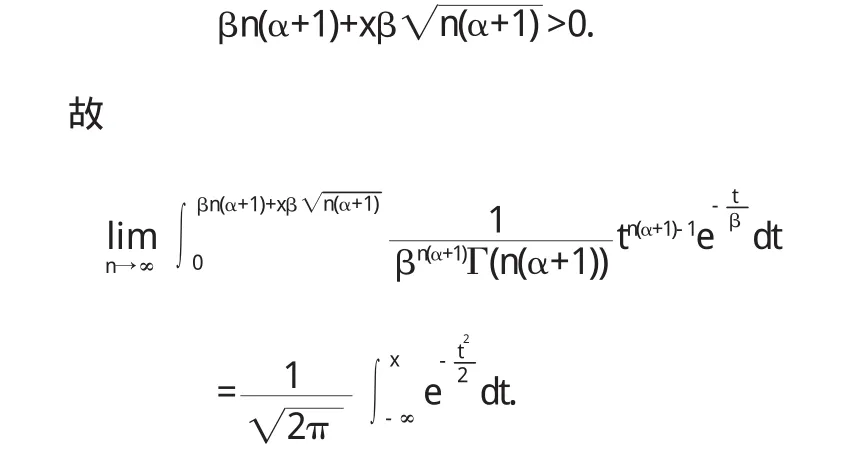
特别地，当α=0时，

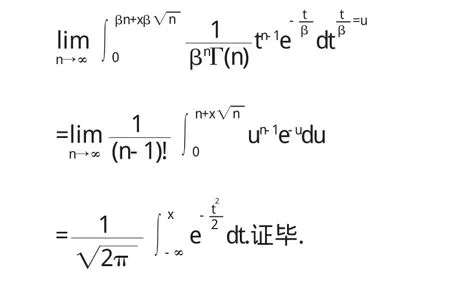
由例2，立即可得下一重要结论：

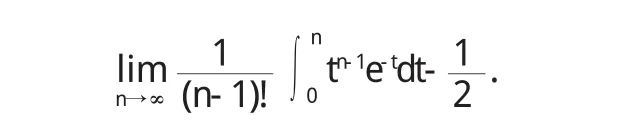
当含参变量的积分的极限与标准正态分布的分布函数有关时，若能将参变量的被积函数与某一连续型随机变量的密度函数联系起来，一般利用中心极限定理就能解决问题.

〔1〕梁之舜，邓集贤，杨维权，等.概率论与数理统计[M].北京：高等教育出版社，2005.267－290.

〔2〕陆传荣，林正炎，陆传赉.概率论极限理论引论[M].北京：高等教育出版社，1989.89－105；128－155.