基于朴素贝叶斯分类算法的股指预测研究
2014-09-22任民宏肖海蓉
任民宏, 肖海蓉
(陕西理工学院 数学与计算机科学学院, 陕西 汉中 723000)
基于朴素贝叶斯分类算法的股指预测研究
任民宏, 肖海蓉
(陕西理工学院 数学与计算机科学学院, 陕西 汉中 723000)
预测大盘指数的涨跌幅度在股票投资中具有重要的意义。大盘指数的涨跌既与国家的宏观经济政策有关,也与大盘指数自身运行状态有关。结合朴素贝叶斯分类算法和股票大盘指数涨跌的影响因素建立了大盘指数分类预测模型,以上证指数为例进行了实验,结果表明分类预测模型有效,准确性较高。
朴素贝叶斯分类算法; 大盘指数; 预测模型
0 引 言
股市是一个高风险高收益的投资场所,如何能正确预测大盘指数的涨跌幅度,帮助投资者减少风险、提高收益,这个问题一直以来倍受人们的关注。
大盘指数是对股票价格的反映,影响股票价格的因素既与整个社会经济环境和国家的宏观经济政策有关,也与自身运行状态有关,甚至投资者的心理因素也影响股市,而且这些因素以非常复杂的方式相互影响。因而预测大盘指数的涨跌幅度通常是比较困难的。近年来,随着人工智能尤其是专家系统的发展,人工神经网络被用来预测大盘指数和股票价格,这能有效解决股市预测的困难,但是人工神经网络容易受到网络的权重初始化不合理而影响预测的速度和准确性,不能考虑社会经济环境和国家的宏观经济政策对股市的影响。
本文综合考虑影响股票价格的主要因素,建立了基于朴素贝叶斯分类算法的大盘指数分类预测模型。
1 朴素贝叶斯分类算法
朴素贝叶斯分类算法基于贝叶斯定理,以计算类别所属的概率达到分类预测的目的,它是一种统计分类方法。对分类算法的比较研究可以发现,朴素贝叶斯分类算法的分类性能可以与决策树和人工神经网络分类算法相媲美。
朴素贝叶斯分类算法的基本原理如下[1]:
(1)每个数据样本用一个n维向量X={x1,x2,…,xn}表示,分别描述对n个属性A1,A2,…,An样本的n个度量。
(2)假定有m个类别C1,C2,…,Cm,给定一个未知类别的数据样本X,分类器在已知X的情况下,预测X属于具有最大后验概率的那个类别。即样本X归属到类别Ci当且仅当
P(Ci|X)>P(Cj|X), 1≤j≤m,i≠j,
其中P(Ci|X)最大的类别Ci称为最大后验假设。根据贝叶斯定理有:
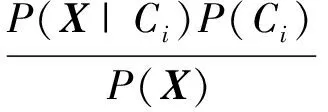
(1)
(3)P(X)的计算公式为:
(2)
P(X)对所有的类别都为常数,因而只需要P(X|Ci)P(Ci)最大即可。P(Ci)称为类别的先验概率,可通过P(Ci)=Si/S公式计算,其中Si为训练样本集中类别Ci的样本数,S为训练样本集中样本数。
(4)若给定包含多个属性的数据集,直接计算P(X|Ci)的开销可能非常大。为降低计算的开销,朴素贝叶斯分类算法通常假设所有属性所起的作用都是独立的,于是对于特定的类别,有:
(3)
可以根据训练样本估算P(xk|Ci)的值,具体的处理方法如下:
①如果属性Ak是符号量,就有P(xk|Ci)=Sik/Si,其中Sik为训练样本集中类别为Ci且属性Ak取值为vk的样本数,Si为训练样本集中类别为Ci的样本数。
②如果属性Ak是连续量,那么假定属性具有高斯分布,因此就有:
(4)
其中μCi和σCi为训练样本集中类别为Ci的属性Ak的均值和方差。
(5)为预测一个未知样本X的类别,可对每个类别Ci估算相应的P(X|Ci)P(Ci)。样本X归属类别Ci当且仅当P(Ci|X)>P(Cj|X)(1≤j≤m,i≠j)。
2 大盘指数分类预测模型
2.1 训练样本的确定
大盘指数分类预测就是根据大盘指数的历史数据,运用分类算法进行数据分析,得出大盘指数的涨跌幅度[2-3]。
笔者选取上证指数从2008年4月22日至2009年2月13日的数据为训练样本。确定样本属性时,既考虑了股票的短线指标,又结合了国家经济政策消息对股指的影响,最终确定的训练样本如表1所示,由于篇幅所限,这里只列出部分数据。

表1 训练样本数据
样本属性“BIAS指标”、“KDJ指标”和“BOLL指标”是股票的短线技术指标,其中“BIAS指标”和“KDJ指标”从股票行情软件中取值,“KDJ指标”取J的值[4-5]。“BOLL指标”在股票行情软件中表现为股价K线与上轨线、中轨线和下轨线的位置关系,因而“BOLL指标”的取值为“已达下轨线”、“接近下轨线”、“在下轨线和上轨线之间”、“接近上轨线”和“已达上轨线”。
样本属性“距上一低点或高点涨跌幅”反映股指在短期内的涨跌幅度,其计算公式为:

(5)
样本属性“下一个交易日消息”反映当前国家经济政策消息面是利多还是利空,其取值为“重大利多”、“一般利多”、“一般”、“一般利空”和“重大利空”。
样本属性“上方压力与下方支持力之差”反映多空双方的力量强弱,如果收盘价大于开盘价,其计算公式为:

(6)
否则,其其计算公式为:

(7)
样本属性“下一个交易日涨跌”是分类属性,其取值为“涨幅≥5%”、“1%≤涨幅<5%”、“涨幅<1%”、“跌幅<1%”、“1%≤跌幅<5%”和“跌幅≥5%”。
2.2 预测算法
由于样本属性“BIAS指标”、“KDJ指标”、“距上一低点或高点涨跌幅”和“上方压力与下方支持力之差”的取值都是实数,为了分类方便,需要将这些属性分为几个区间[6-7]。根据股指在峰值点和谷底点的平均值,“BIAS指标”取值分为3个区间:(-∞,-2.749],(-2.749,3.099],(3.099,+∞)。由于股指经常在“KDJ指标”的0和100两处附近的走向发生变化,因而“KDJ指标”取值分为3个区间:(-∞,0],(0,100],(100,+∞)。根据股指走向变化时涨跌幅度大小的平均值,“距上一低点或高点涨跌幅”取值分为6个区间:(-∞,-0.211],(-0.211,-0.095],(-0.095,0],(0,0.084],(0.084,0.198],(0.198,+∞)。根据股指走向变化时“上方压力与下方支持力之差”的平均值,“上方压力与下方支持力之差”取值分为6个区间:(-∞,-0.016],(-0.016,-0.003],(-0.003,0],(0,0.003],(0.003,0.015],(0.015,+∞)。算法描述如下:
1)输入待分类元组t的“BIAS指标”、“KDJ指标”、“BOLL指标”、“距上一低点或高点涨跌幅”、“下一个交易日消息”和“上方压力与下方支持力之差”各属性分量值。
2)统计训练样本数,记为S。
3)计算每个分类值的先验概率,记为P(Cj)(j=1,2,…,6),其计算公式为:

(8)
其中,SCj为训练样本中分类属性为第j个分类值的样本数。
4)计算“BIAS指标”属性值在区间 (-∞,-2.749],(-2.749,3.099]和(3.099,+∞)上的分类概率,记为PBij(i=1,2,3;j=1,2,…,6),其计算公式为:
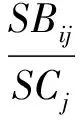
(9)
其中,SBij为训练样本中“BIAS指标”属性值在第i个区间上且分类属性为第j个分类值的样本数,SCj为训练样本中分类属性为第j个分类值的样本数。
5)计算“KDJ指标”属性值在区间 (-∞,0],(0,100]和(100,+∞)上的分类概率,记为PKij(i=1,2,3;j=1,2,…,6),其计算公式为:
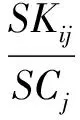
(10)
其中,SKij为训练样本中“KDJ指标”属性值在第i个区间上且分类属性为第j个分类值的样本数,SCj为训练样本中分类属性为第j个分类值的样本数。
6)计算“BOLL指标”属性取值的分类概率,记为POij(i=1,2,…,5;j=1,2,…,6),其计算公式为:
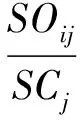
(11)
其中,SOij为训练样本中“BOLL指标”属性值为第i个值且分类属性为第j个分类值的样本数,SCj为训练样本中分类属性为第j个分类值的样本数。
7)计算“距上一低点或高点涨跌幅”属性值的分类概率在区间(-∞, -0.211]、(-0.211, -0.095]、(-0.095,0]、(0, 0.084]、(0.084, 0.198]和(0.198, +∞) 上的分类概率,记为PRij(i=1,2,…,6;j=1,2,…,6),其计算公式为:
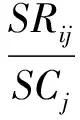
(12)
其中,SRij为训练样本中“距上一低点或高点涨跌幅”属性值在第i个区间上且分类属性为第j个分类值的样本数,SCj为训练样本中分类属性为第j个分类值的样本数。
8)计算“下一个交易日消息”属性取值的分类概率,记为PMij(i=1,2,…,5;j=1,2,…,6),其计算公式为:
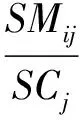
(13)
其中,SMij为训练样本中“下一个交易日消息”属性值为第i个值且分类属性为第j个分类值的样本数,SCj为训练样本中分类属性为第j个分类值的样本数。
9)计算“上方压力与下方支持力之差”属性值在区间(-∞, -0.016]、(-0.016,-0.003]、(-0.003,0]、(0, 0.003]、(0.003, 0.015]和( 0.015, +∞)上的分类概率,记为PSij(i=1,2,…,6;j=1,2,…,6),其计算公式为:
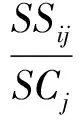
(14)
其中,SSij为训练样本中“上方压力与下方支持力之差”属性值在第i个区间上且分类属性为第j个分类值的样本数,SCj为训练样本中分类属性为第j个分类值的样本数。
10)对于待分类元组t,计算对应于各属性取值的分类条件概率,记为P(t|Cj)(j=1,2,…,6),其计算公式为:
P(t|Cj)=PBit j×PKit j×POit j×PRit j×PMit j×PSit j,j=1,2,…,6,
(15)
其中,PBit j为待分类元组t的“BIAS指标”属性取值对应的分类属性为第j个分类值的分类概率;PKit j为待分类元组t的“KDJ指标”属性取值对应的分类属性为第j个分类值的分类概率;POit j为待分类元组t的“BOLL指标”属性取值对应的分类属性为第j个分类值的分类概率;PRit j为待分类元组t的“距上一低点或高点涨跌幅”属性取值对应的分类属性为第j个分类值的分类概率;PMit j为待分类元组t的“下一个交易日消息”属性取值对应的分类属性为第j个分类值的分类概率;PSit j为待分类元组t的“上方压力与下方支持力之差”属性取值对应的分类属性为第j个分类值的分类概率。
11)计算待分类元组t归类到每个分类的后验概率,记为P(Cj|t),其计算公式为:
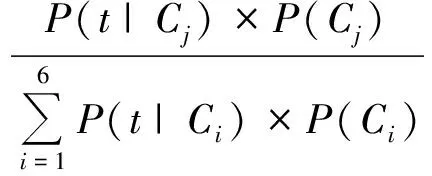
(16)
12)将待分类元组t归类到类别Ci,当且仅当P(Ci|t)>P(Cj|t) (1≤j≤6,i≠j)。
2.3 实验结果及分析
采用上面提出的预测模型,笔者对2009年2月16日至2009年3月27日共30天交易日上证指数进行预测,实验采用VB6.0编程实现,结果如表2所示,其中有26个交易日指数涨跌幅预测正确。
实验结果表明,采用本文中提出的预测模型可以有效地预测大盘指数当天的涨跌幅,预测正确率为86.67%。
3 结 语
本文提出的大盘指数分类预测模型以朴素贝叶斯分类算法作为分类器,能有效预测股指当天的涨跌幅度。在模型中既考虑了股票的短线指标,又结合了国家经济政策消息面对股指的影响,从实验结果来看,当国家经济政策消息面比较明朗的情况下该分类预测模型准确性较高。
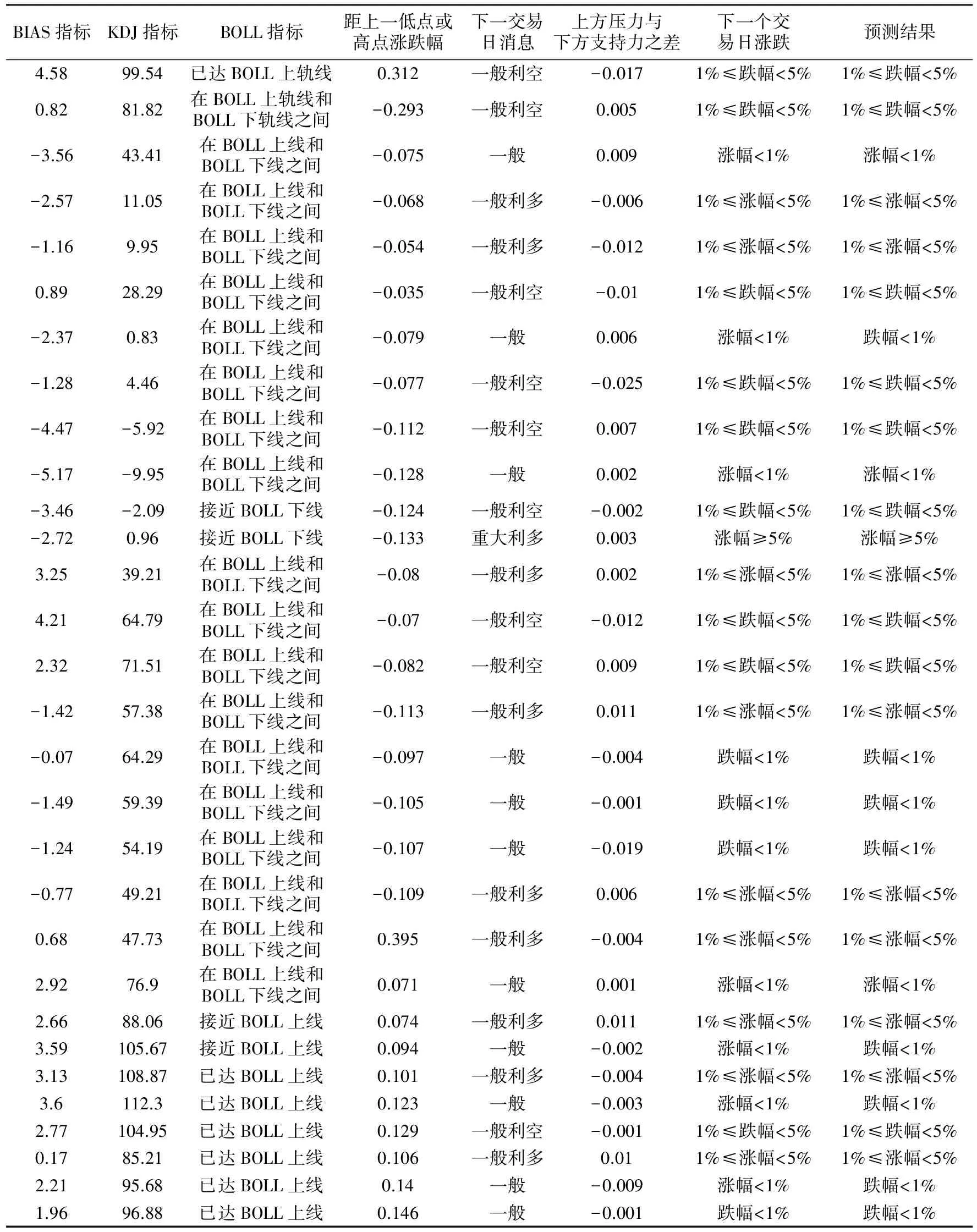
表2 实验结果
[1] MARGARET H Dunham.数据挖掘教程[M].郭春慧,天凤占,靳晓明,译.北京:清华大学出版社,2005:74-75.
[2] 吕昊,林君,曾晓献.改进朴素贝叶斯分类算法的研究与应用[J].湖南大学学报:自然科学版,2012,32(12):56-61.
[3] 左辉,楼新远.基于贝叶斯分类的选股方法[J].电脑知识与技术,2008(10):173-176.
[4] 刘红岩.商务智能方法与应用[M].北京:清华大学出版社,2013:40-42.
[5] 余芳,姜云飞.一种基于朴素贝叶斯分类的特征选择方法[J].中山大学学报:自然科学版,2004,43(5):118-120.
[6] 冯现坤,刘羽,蒋细芳.朴素贝叶斯分类算法在数据预测中的应用[J].软件导刊,2011,10(5):65-66.
[7] 田志伟.贝叶斯神经网络在股票预测中的应用[D].无锡:江南大学,2011:10-12.
[责任编辑:李 莉]
Abstract: Margin prediction for the broader market index is of great significance in stock investment. Broader market index is not only related to national macroeconomic policies, but also related to the broader index operation itself. Based on native Bayes classification algorithm and influence factors of stock market index, a classification prediction model is established about market index, and followed by an experiment of Shanghai stock index as a case study. The experiment results prove that the classification prediction model is effective with higher accuracy.
Keywords: native Bayes classification algorithm; market index; prediction model
On stock index prediction based on native Bayes classification algorithm
REN Min-hong, XIAO Hai-rong
(School of Mathematics and Computer Science, Shaanxi University of Technology, Hanzhong 723000, China)
1673-2944(2014)03-0068-06
2013-11-18
任民宏(1970—),男,陕西省洋县人,陕西理工学院副教授,硕士,主要研究方向为计算机图形图像处理、数据挖掘;肖海蓉(1976—),女,陕西省泾阳县人,陕西理工学院讲师,硕士,主要研究方向为数据库技术、计算机图形图像处理。
F830.91; TP181
A
