基于蒙特卡洛模拟的VaR模型及其模拟实证对比研究

喻为民

(淮南联合大学 基础部，安徽 淮南 232038)

随着经济全球化和金融一体化的迅猛发展，国际范围内的金融市场创新活动逐步深入，由此带来金融风险的管理控制问题成为理论界讨论的重点问题。VaR模型最早由J.P.Morgan提出［1］，被广泛的运用到金融风险的测量上并取得迅速推广，成为金融市场衡量风险的主流方法。

1 VaR模型的基本思想

1.1 VaR模型的金融学含义

VaR是“Value at Risk”的简写，一般被称作是“处于风险中的价值”或“风险价值”，其经济学含义表征为在市场正常波动情况下，某一金融资产或证券组合的最大可能损失。通过VaR值的确定，可以知道投资者在某一市场波动范围内进行某次投资行为所能够承受的最大可能损失［2］。比如A资产组合未来24小时的90%的VaR值为100万元人民币，即表示投资者购买A组合未来一天内可以保证90%的可能性，其最大损失不超过100万元。

1.2 VaR模型的数学含义

VaR的数学含义可以表示为在给定的置信水平范围内，某一金融资产或证券组合在特定时间范围内的最大可能损失。即置信水平C条件下，持有某金融资产Δt时间其所能够承受的最大可能损失为VaR。其数学表达式如下:

其中ΔPΔt表示持有该金融资产Δt时间内所遭受到的损失。一般而言损失应当负数表示，但考虑到日常习惯，此处ΔPΔt和VaR均为正数。公式(1)和(2)分别表示实际损失不超过和超过VaR值的概率水平，即此处的置信水平C。

2 基于蒙特卡洛模拟的VaR模型数学解释

历史模拟法的重点在于科学确定投资组合的价值函数及市场因子的分布水平，并假设投资组合的价值函数与市场因子之间存在线性关系。以RiskMetrics为主要代表的历史模拟法，往往假定市场因子的分布服从多元正态分布，对于构建和计算VaR值提供模型上的简便，不同置信水平和不同持有期的VaR值均可以得以转化计算出［2］。但是其模型假定中市场因子收益的多元正态分布情况与现实存在较大差距，且对于非线性金融工具的风险衡量不够充分。

与历史模拟法不同，蒙特卡洛模拟法以计算机基于一定规则随机生成的数据作为计算VaR值的依据，通过随机数模拟出市场因子的各种可能分布情况，从而计算出投资组合的VaR值。蒙特卡洛模拟法通过随机生成的序列近似模拟各种可能分布情况下市场因子的各种潜在情况，并利用这些随机数计算出不同置信水平条件下的VaR值。作为一种全估值的模拟方法，基于蒙特卡洛模拟的VaR计算方法一方面有效地克服非线性价格风险、粗尾风险等不利因素的影响，另一方面则提供各种不同分布条件情况下的收益行为及VaR值。

本文以蒙特卡洛模拟作为计算VaR值的主要方法，并通过数学语言重点解释VaR值计算的完整过程。一般而言，基于蒙特卡洛模拟的VaR值计算包括三个主要步骤，首先是基本规则提出及随机模型的构建;其次是基于随机规则的模拟价格序列生成;最后则是基于随机生成的数据估算VaR值。

2.1 随机模型构建

在初始时刻t到目标时刻T持续期内，假设投资组合的价格S为时刻t的函数，即t时刻投资组合价值为S(t)。记其一阶差分为y(t)，投资组合相邻时刻价格之间存在某种数学关系，公式表示如下［4］:

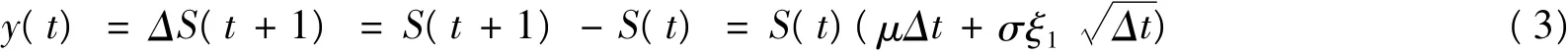
其中μ，σ分别表示投资组合的均值和标准差，ξ为服从标准正态分布的随机变量，通过ξ数值的不同可以随机生成不同的模拟数值。

2.2 模拟价格走势

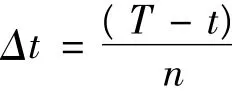
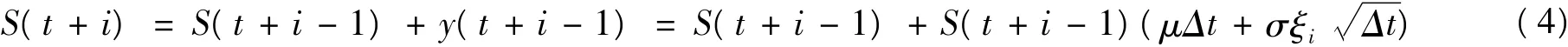
其中i=1，2，……n。通过公式(4)基于生成的随机变量ξi可以模拟出n个时间间隔单元内的价格序列{S(t+1)，S(t+2)，……S(t+n)}及目标时刻T的价格S(T)=S(t+n)。

2.3 VaR估值

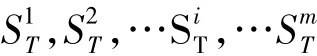
选取该院收治的100例糖尿病患者，所有患者于该院进行检查均确诊为糖尿病，排除严重肝肾疾病、躯体疾病、恶性肿瘤、语言障碍及精神障碍者，100例患者及其家属均对该研究知情同意，并签署知情同意书。按照随机数字表法将其分为对照组和观察组，每组各50例；对照组男性27例，女性23例，年龄21～74岁，平均年龄（47.5±4.5）岁，病程 1～14 年，平均病程（7.5±1.2）年；观察组男性25例，女性25例，年龄22～75岁，平均年龄（48.5±4.2）岁，病程 1～13 年，平均病程（7.2±4.1）岁，两组患者性别、年龄、病程一般资料差异无统计学意义（P＞0.05），具有可比性。

根据已得的目标时刻价格序列，将其模拟价格按照从小到大的顺序升序排列组成新的序列L'。在给定置信水平C条件下，选取新序列L'中的第m(1-C)个数作为衡量值，记其为S'，则S'=，i=m(1-C)。通过相对计算方法可以将VaR值表示如下:

假设重复价格走势5000次，在置信水平90%条件下，在蒙特卡洛模拟方法计算VaR模型的要求下，将某投资组合目标时刻价格序列按照升序进行排列，选取第5000×(1-90%)=500个数作为衡量值，在与基期价格St进行求差运算，即可求出90%置信水平条件下的该种投资组合的VaR值。

2.4 VaR数值的检验

通过以上三步的完整实施，可以计算出基于蒙特卡洛模拟的投资组合的VaR值，从而用于该投资组合的风险管理问题。由于在运用蒙特卡洛模拟过程中，随机数的生成过程中不可避免会出现伪随机数问题，对于计算出的VaR数值的科学性和实用性产生一定程序上的影响［6］。因此有必要在完成VaR数值计算之后，对计算结果通过科学的方法进行检验，以验证其准确性。

VaR数值检验在于检验投资组合的实际损失与VaR值之间的偏离概率是否在给定置信水平范围内的，其检验方法众多，本小节将介绍失败频率检测法［7-8］。在失败频率检测法中，假设记实际损失超过VaR值为失败，记实际损失不超过VaR值为成功，考察天数为X天，在给定置信水平C条件下，失败天数为Y天。则

对VaR数值结果进行验证即验证失败频率P与失败期望概率P*之间是否相等，通过假设检验与参数估计的方法即可求出零假设H0:P=P*的置信域［9］。

3 VaR模型的随机模拟实现

结合前部分的成果，本部分将利用Matlab2012a实现VaR模型的随机模拟计算。此处通过随机模拟函数生成2000天的收益率r，在置信水平位99%条件下，分别假设收益率r服从标准正态分布和自由度为4的t分布，计算近1000天的VaR值及收益r。计算结果如下:

3.1 r服从标准正态分布

基于Matlab2012a的计算，其结果如下图所示:

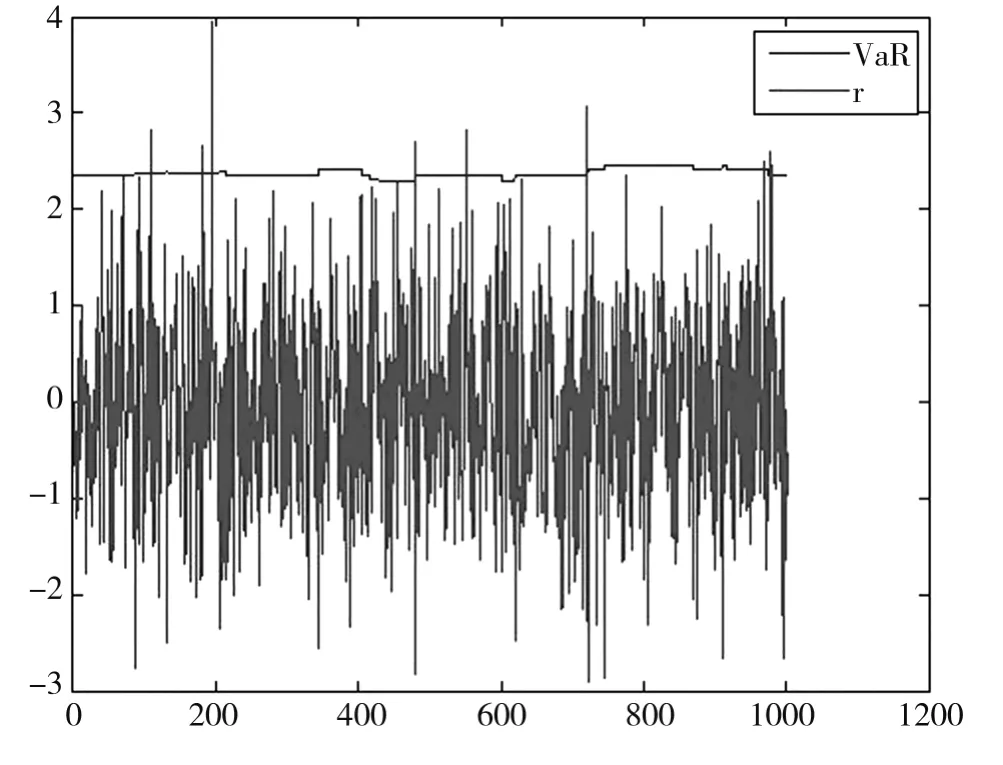
图1 服从标准正态分布的计算结果

由图1可以看出，通过假设收益率r服从标准正态分布生成模拟数，并结合VaR数值的滚动求解，近1000天投资组合的收益率大多分布于6σ范围区间内，VaR数值约为2.21大小左右。

3.2 r服从t分布(n=4)

基于Matlab2012a的计算，其结果如下图所示:

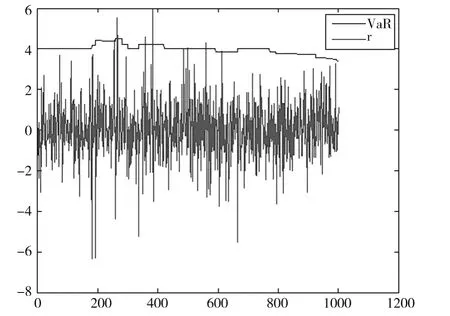
图2 服从t分布的计算结果(自由度n=4)

由图2可以看出，通过假设收益率r服从自由度为4的t分布生成模拟数，并结合VaR数值的滚动求解，近1000天投资组合的收益率大多分布于±6范围区间内，且存在诸多极端数值，VaR数值约为4.02大小左右。

3.3 主要结论

综合以上两个图形可以看出，在收益率分别服从标准正态分布和自由度为4的t分布的VaR计算结果中，t分布结果图形较好的反映出来金融数据的厚尾与尖峰特征。在置信水平位99%的条件下，收益率服从t分布的VaR数值明显高于收益率服从标准正态分布的VaR值。在高置信水平条件下，t分布模型较于标准正态分布模型具有更高的精度要求和显著的优势。此外t分布模型在描述投资组合收益率方面，明显地表征出金融收益率数据的波动性和非稳定性，对金融数据的厚尾及尖峰特征进行较好的拟合。

4 VaR模型的历史模拟实现

结合前部分的成果，本部分将利用Matlab2012a实现VaR模型的历史模拟计算。以2012年1月1日至2013年12月30日，从交易开拓者导出上海中金期货交易所股指期货的历史日线数据，并计算其收益率。再通过Matlab予以分析。考虑到股指日波动性较大，本部分所选取的原始数据是股指的日平滑指数。以全年交易日数为横轴，以每日VaR值为纵轴，计算结果如下图所示:

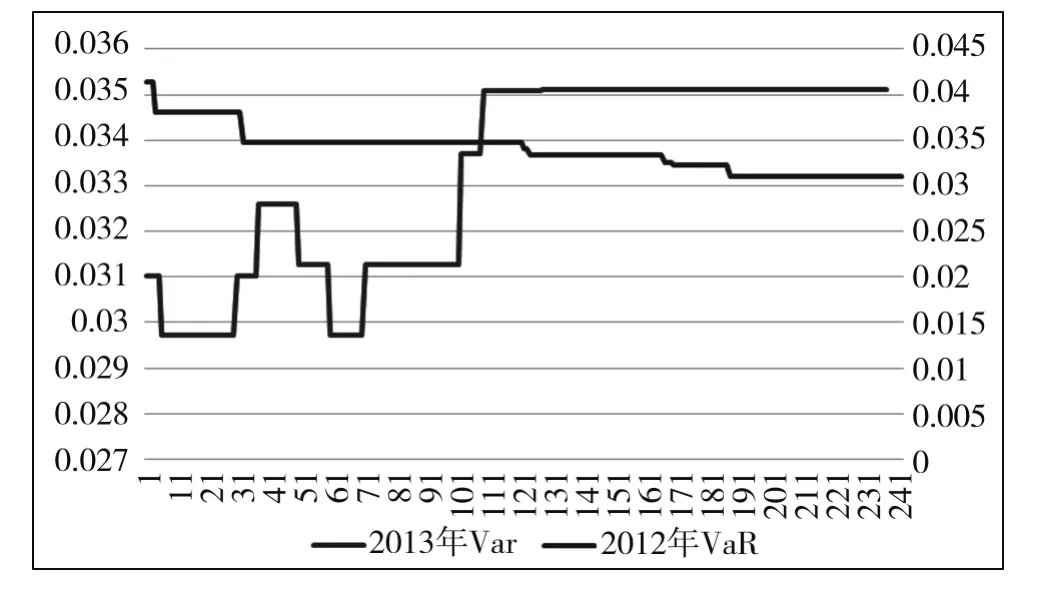
图3 2012年与2013年股指VaR比较图

由上图可以看出，2012年至2013年我国股指期货的市场结构发生较为明显变化。具体而言，2012年全年股指期货市场风险波动幅度较小，2013年全年股指期货市场风险波动幅度较大。2013年上半年我国股指期货市场的系统风险较低，但是波动水平较为剧烈，下半年系统风险走高。与2012年的股指期货市场相比，2013年股指期货系统风险结构发生变化，对市场内广大参与者造成一定程度的影响。由此可见，对于市场内的参与者而言，要注意利用VaR值来衡量系统，指导其未来的交易行为。

5 结语

本文从金融学和数学角度出发阐述VaR的基本涵义，在此基础上通过VaR模型计算方法的综述，运用数学语言构建基于蒙特卡洛模拟的VaR求解模型，再利用Matlab通过历史模拟和随机模拟分别测度出99%置信水平条件下金融市场的VaR数值。通过对比分析，研究结果表明:随机模拟方面，t分布模型在高置信水平条件下较标准正态分布模型具有更高的精度要求和优势，且对于金融收益率数据的表征更为合理科学;历史模拟方面，2013年我国股指期货市场结构较2012年发生较大程度变化，且系统风险有进一步扩大趋势。

［1］Fernandez V.Risk Management Under Extreme Events［J］.International Review of Financial Analysis，2005(14):113-148.

［2］Turan G B，David W.A conditional extreme value volatility estimator based on high frequency returns［J］.Journal of Econometrics，2007，3(2):361-397.

［3］黄海，卢祖帝.VaR的主要计算方法述评［J］.管理评论，2003(7):31-36.

［4］杜平，徐济东.用VaR度量与管理投资基金的市场风险［J］.经济问题探索，2007(7):67-71.

［5］徐炜，黄炎龙.GARCH模型与VaR的度量研究［J］.数量经济技术经济研究，2008(1):120-132.

［6］刘子斐，史敬.VaR模型比较技术及其评价——理论、实证回顾及其应用初探［J］.金融研究，2008(5):130-137.

［7］周革平.VaR基本原理、计算方法及其在金融风险管理中的应用［J］.金融与经济，2009(2):69-72.

［8］王春峰，张亚楠，房振明，等.基于极值理论的高频条件VaR动态区间估计模型［J］.系统工程理论与实践，2010(7):1162-1168.

［9］盛世明.基于连接函数的VaR的蒙特卡洛算法［J］.统计与决策，2010(21):27-29.