误差修正机制转换模型的贝叶斯估计

丁 辉，王咪咪

(滁州学院 数学科学学院，安徽 滁州 239000)

0 引言

误差修正模型(ECM)既能描述不同时间序列变量之间的长期均衡关系，又能反映出时间序列变量间的短期非均衡关系向长期均衡关系修正的机制，是分析时间序列变量之间长期和短期综合影响的一个强有力的工具。然而在现实经济实体中，由于市场上存在着交易费用与经济政策的突变，导致时间序列变量之间的长期均衡关系并不是一直都存在，发生了结构机制上的突变。而针对结构机制上的突变这种现象，Hamilton［1］提出了马尔科夫机制转换模型(MS模型)。该模型可以有效地描述经济变量在不同机制下的行为特征。因此将马尔科夫转换机制引入到误差修正模型中，便形成了误差修正机制转换模型(简称MSECM)。该模型既有效地描述了变量之间的长期和短期综合关系，又解决了现实经济实体中协整关系的机制改变难题，因此在经济领域中得到了广泛的应用。

到目前为止，关于误差修正机制转换模型甚至马尔科夫机制转换模型的参数估计方法主要是极大似然估计法或者近似极大似然估计法［2］。极大似然估计方法属于经典估计方法，并没有结合样本数据的先验信息。而贝叶斯估计法相对于经典估计，结合了数据的信息与参数的先验信息，而且还能对缺失数据、截尾数据等进行简明化处理，因此相对与其他经典估计具有无与伦比的优势。下面将使用贝叶斯估计法来估计误差修正机制转换模型中的未知参数。

1 误差修正机制转换模型及其相关概念

假设{xt}、{yt} 是两个一阶单整时间序列，即xt～I(1)，yt～I(1)。并设x1，x2，…，xn;y1，y2，…，yn分别为这两个序列的观测值。误差修正机制转换模型的形式如下:

当xt、yt之间存在协整关系时，则xt、yt满足误差修正模型，即:

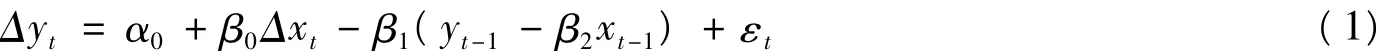
其中ecm=yt-1-β2xt-1为误差修正项，Δyt=yt-yt-1，Δxt=xt-xt-1，随机误差项εt是一个白噪声过程，它们相互独立，且都服从正态分布N(0，σ2)。

当xt、yt之间不存在协整关系时，则xt、yt不存在长期均衡关系，即β1=0，模型变为

为了简化误差修正机制转换模型的形式，引入机制变量st，当st=1时表示xt、yt存在协整关系，当st=0时表示xt、yt不存在协整关系，且机制变量st满足:

于是误差修正机制转换模型的一般形式表达如下:

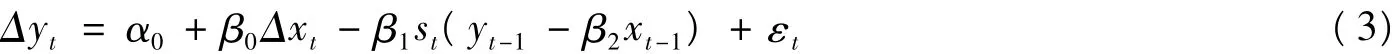
其中 εt～ N(0，σ2)。

2 误差修正机制转换模型的贝叶斯估计

2.1 模型简化

为了对该模型应用贝叶斯估计，对该模型进行进一步的简化。令

则模型简化为:

2.2 参数的先验分布

为了消除信息不准确时先验分布对贝叶斯估计带来的估计影响，采取无信息先验分布［3］。

假设参数β服从均匀分布，即f(β)∝1;

参数σ2服从均匀分布，即f(σ2)∝1;

参数p11服从均匀分布U(0，1)，即f(p11)∝1;

参数p00服从均匀分布U(0，1)，即f(p00)∝1。

2.3 模型的似然函数

模型(4)的似然函数为

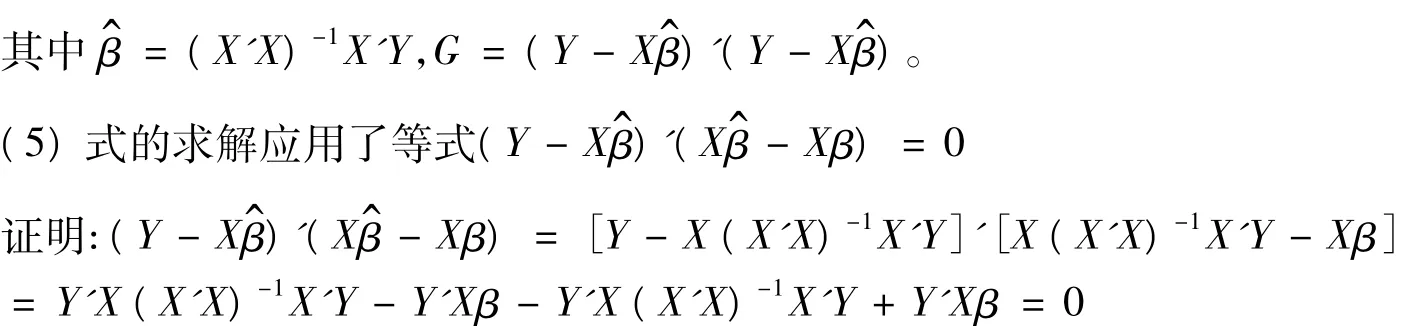
2.4 参数的后验分布

机制变量S的分量之间高度相关，因此若使用满条件后验分布去实现机制变量S的估计是无效的［4］。为此，采用 Frühwirth-Schnatter［5］和 Carter、Kohn［6］提出的 FFBS 算法来实现机制变量 S 的估计。

令 Xt=(x1，x2，…，xt)'，Yt=(y1，y2，…，yt)'，则由贝叶斯定理可知

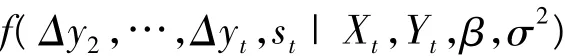
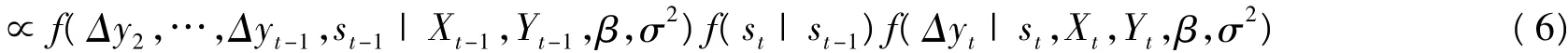
FFBS具体算法:首先计算pn(0)，并从均匀分布U(0，1)中产生随机数，若该随机数小于pn(0)，则sn=0，否则sn=1;然后根据(7)式得到的概率，按照完全相同的方法从后往前依次抽取sn-1，sn-2，…，s1，即得到机制变量S的抽样。

机制变量S求出后，则有β，σ2的联合后验分布为

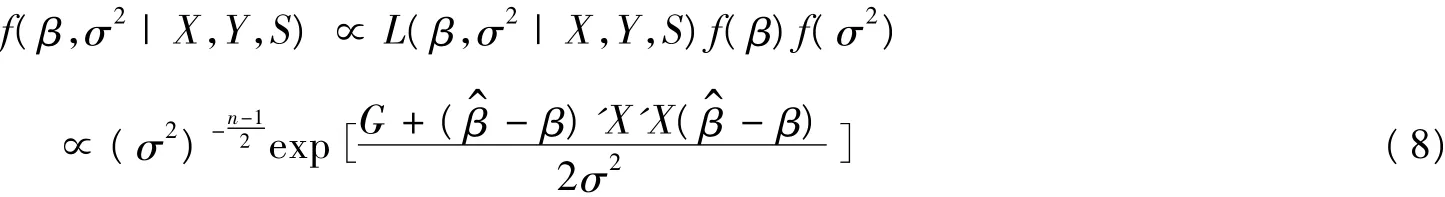
对(8)式关于β积分，得σ2的后验分布为

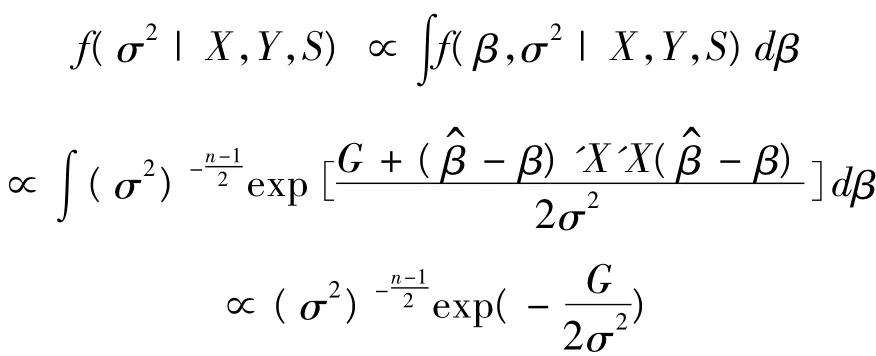
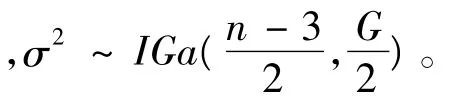
对(8)式关于σ2积分，得β的后验分布

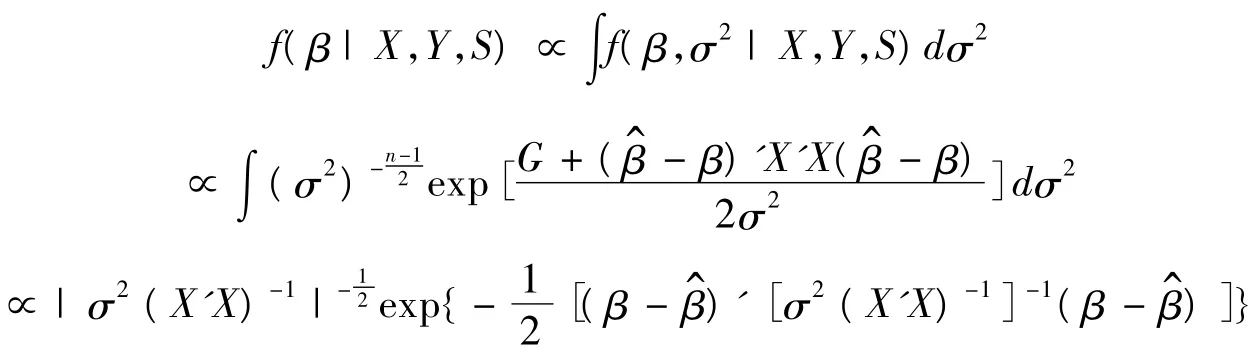
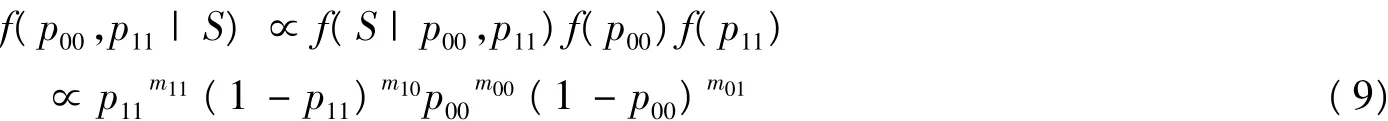
其中mij(i=0，1;j=0，1)表示机制变量st从机制i变化到机制j的次数。

对(9)式关于p00积分，得p11的后验分布

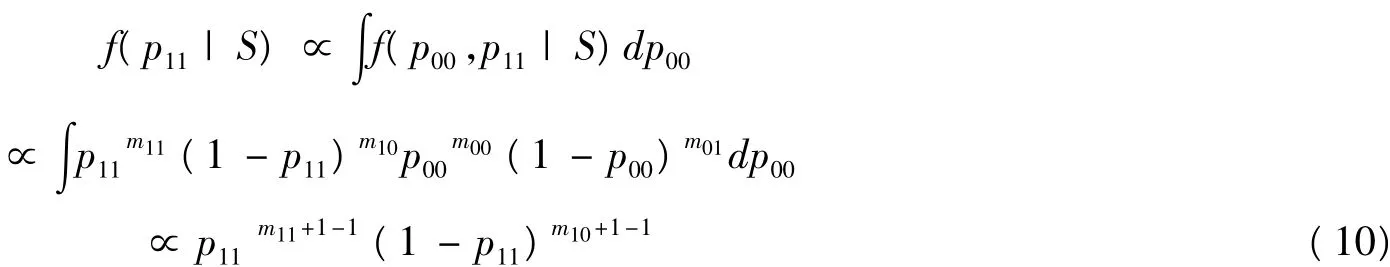
即参数p11服从Beta分布，p11～beta(m11+1，m10+1)。

对(9)式关于p11积分，得p00的后验分布

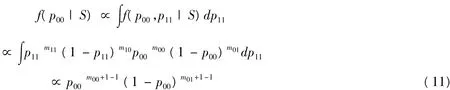
即参数p00服从Beta分布，p00～beta(m00+1，m01+1)。

至此，模型中各个参数的后验分布均已求出，因此可以使用基于Gibbs抽样的贝叶斯估计技术［7］对模型进行参数估计。现将该模型贝叶斯估计的算法说明如下:

Step1:给定 β，σ2的初值 β(0)，σ2(0)，令i=1。

Step 2:使用FFBS抽样算法抽取状态变量S(i)。

Step 5:从beta(m11+1，m10+1)抽取参数

Step 6:从beta(m00+1，m01+1)抽取参数

Step 7:令i=i+1，回到步骤3。

将Step 2至Step 7运行T次，直至参数估计的马氏链收敛为止，并且将参数估计的前M次取值舍去，用以消除参数初值对估计造成的影响。

3 统计模拟

为了测试误差修正机制转换模型的贝叶斯估计方法的性能，设定模型如下:

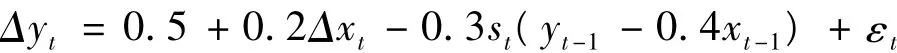
其中 εt～N(0，0.01)，p00=0.93，p11=0.96。

使用统计软件随机生成了500组上述模型的时间序列数据，接着对该时间序列数据应用上述贝叶斯估计方法进行估计，一共迭代10000次，接着删除前面的2000次数值，用以消除初值对参数估计的影响，得到各个参数估计的图(由于篇幅限制，这里仅给出S、α0、β0的参数估计图)。

由图1、图2可以看出机制变量S的真实值与S的估计值除去几个个别值之外估计非常准确，估计效果较好。

由图3、图4可以看出可以α0、β0及其他参数的参数估计值均已收敛，接着进一步求出各个参数估计结果，如表1所示:

图1 机制变量S的真实值

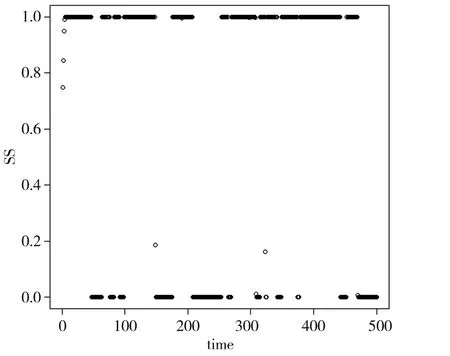
图2 机制变量S的估计值

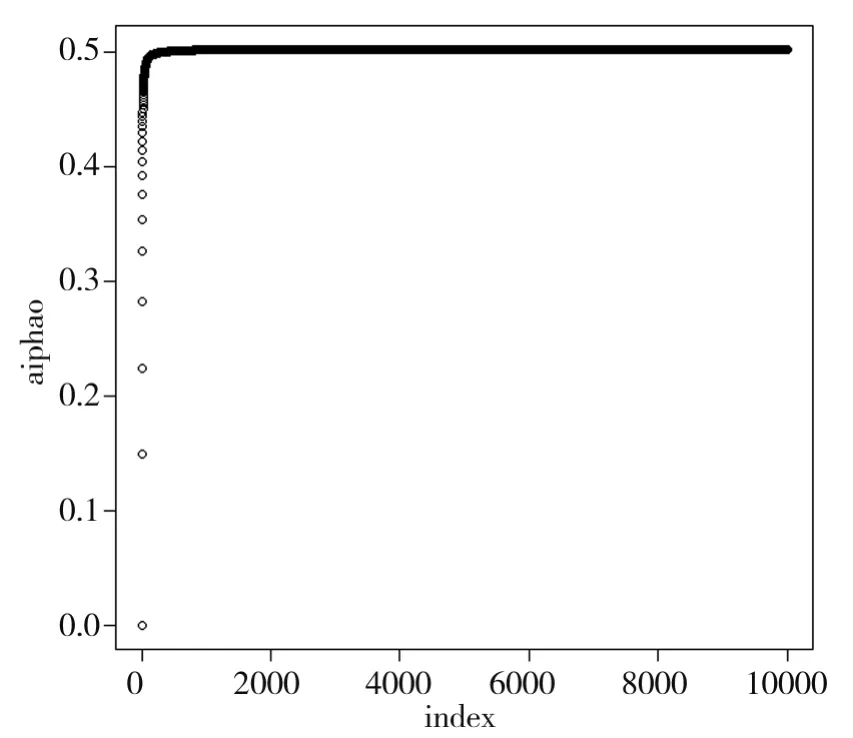
图3 变量α0的估计值

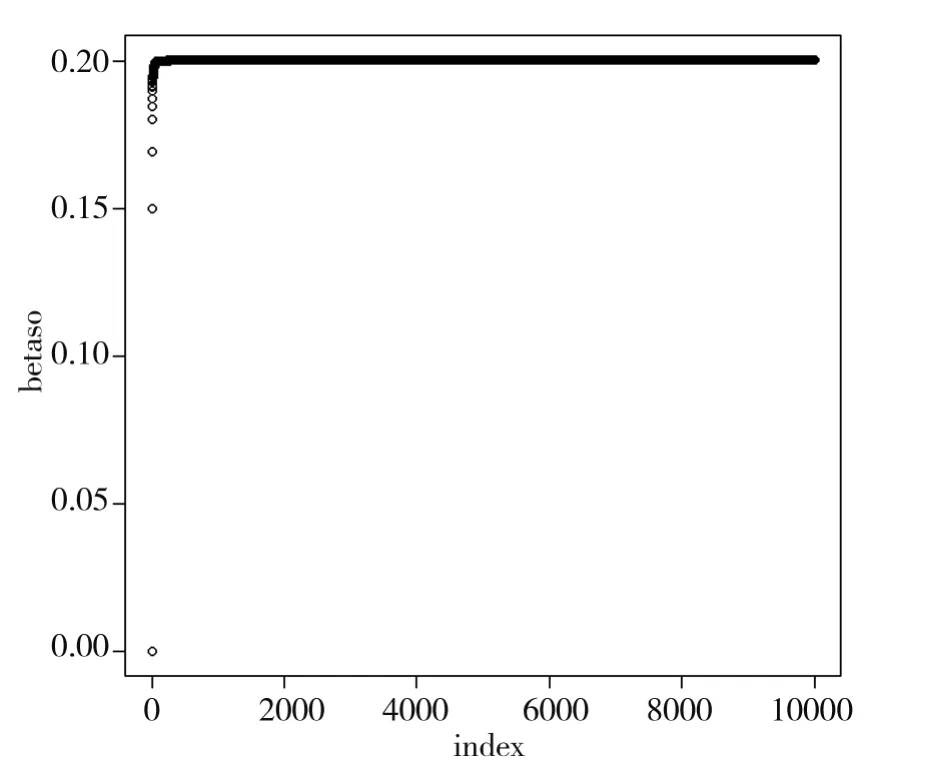
图4 变量β0的估计值

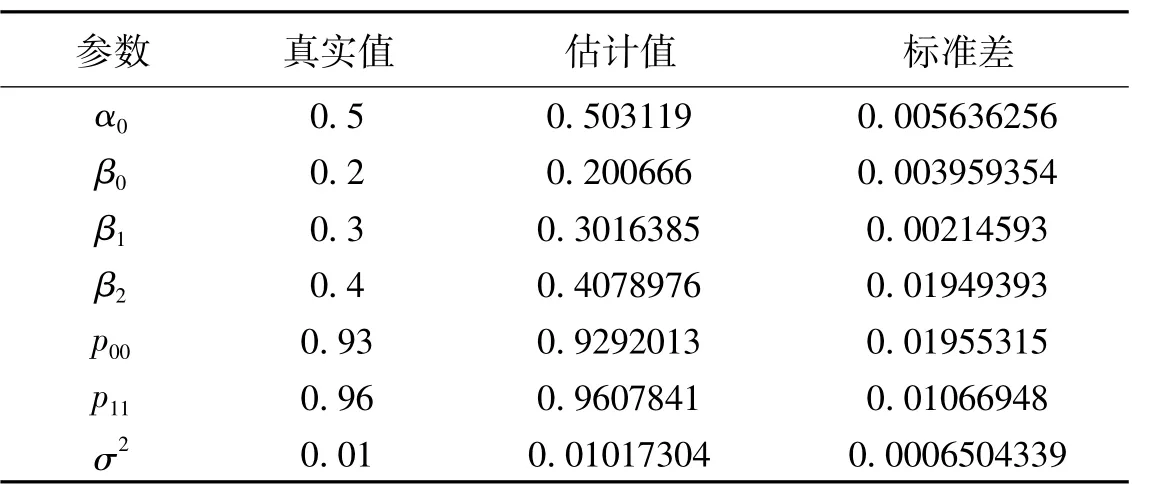
表1 误差修正机制转换模型的参数估计

由表1可以看出，使用的贝叶斯估计法可以稳健的估计出误差修正机制转换模型的参数，该贝叶斯估计方法是可靠的。

4 结论

误差修正机制转换模型是金融时间序列模型中应用较为广泛的一类。不同于经典的极大似然估计方法，通过无信息先验分布的设定，借助于FFBS算法和贝叶斯定理求出各个未知参数的后验分布，并且使用基于Gibbs抽样的贝叶斯估计技术实现了参数估计，由统计模拟的效果来看，该方法估计效果较好，对于今后机制转换模型的深入讨论提供了重要的参考工具。

［1］Hamilton.A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle［J］.Econometrica，1989，57(2):357-384.

［2］原子霞，杨政.马尔科夫协整回归模型的动态滤波估计［J］.控制理论与应用，2013，30(3):360-364.

［3］邹鲲，廖桂生，李军.等.基于Bayes框架的复合高斯杂波下稳健检测［J］.电子与信息学报，2013(7):1555-1561.

［4］G.E.B.Archer and D.M.Titterington.Parameter Estimation for Hidden Markov Chains［J］.Journal of Statistical Planning and inference，2002，108(1):365-390.

［5］Frühwirth-Schnatter.Data augmentation and dynamic linear models［J］.Journal of Time Series Analysis，1994，15(2):183-202.

［6］Carter，Chris，Robert Kohn.On Gibbs sampling for state space models［J］.Biometrika，1994，81(3):541-553.

［7］茆诗松，王静龙，濮晓龙.高等数理统计［M］.2版.北京:高等教育出版社，2006.