双平行簧片结构弹性元件的抗扭转优化设计

李一全，吴雅博

(长春理工大学 机电工程学院，长春 130022)

0 引言

20世纪80年代中后期兴起的微型机电系统(Micro-electro mechanical System，简称MEMS)，它将机构、电源和传感器等集成在一个硅片上，在生物、医药、环境控制领域展现了巨大的发展潜力［1］。但是微型机电系统中的摩擦磨损成为阻碍其发展的一个重大障碍。为了研究微机电系统中的摩擦磨损特性，迫切需要开发适用于微小摩擦磨损检测系统。目前该系统多采用双平行簧片结构作为检测微摩擦力的微力弹性元件，然后通过光学方法检测微力弹性元件的变形量获得微摩擦力的大小［2-4］。

1 双平行簧片结构力学传感器

双平行簧片结构力学传感器的结构与受力分析如图1所示，其结构是一种平行四边形结构，由截面为矩形的簧片组成，簧片的一端固定，当簧片的固定端连接的平行块受测量力P作用时，簧片受力变形，簧片内部应力应变关系是线弹性的，簧片材料为均匀的各项同性的材料，处于平行对称的双平行簧片布置，所以簧片受力相同，变形一致，簧片变形将带动平行块发生平行移动。通过测量平行簧片结构的变形，根据变形与受力关系，就可以计算出测量力P。

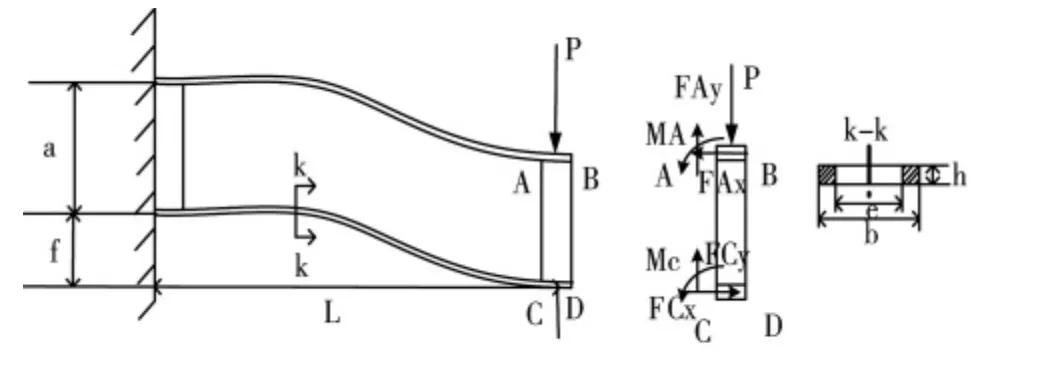
图1 双平行簧片结构与受力分析

两个单片弹簧AB和CD平行固定连接，两弹簧片一侧端部A与C固定在固定板上，另一侧端部B与D固定在活动板上。在外载荷P作用下，簧片变形为［5］:

(1)式中:f为活动板的位移量，即平行型片弹簧的挠度;θ为活动板的转角，即平行型片弹簧的端部转角;E为片弹簧材料的弹性模量;b为片弹簧的总宽度;e为片弹簧的挖空宽度;h为片弹簧的厚度。

由公式(1)可知，只要改变片弹簧各个参数，就可以制作出不同量程、不同分辨率的平行型片弹簧。在理想状态下，平行型片弹簧的上下片弹簧受力后产生的弹性变形完全相同，活动板只有平动没有转动;但是在实际测量应用中，我们发现平行块不仅仅受到力的作用，还要受到由力从探针转移到平行块所产生的附加扭矩作用，这个附加扭矩必将导致平行块转动，假设平行块转动将所产生的转角为φ，如图2所示，利用三角测量方法检测平行块的移动量原理图，这个转角φ将会导致在光斑在光敏面上移动ΔS，此时平行块移动量H和光斑位移S的关系式将变为:

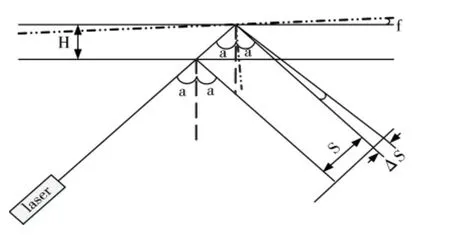
图2 三角位移测量原理

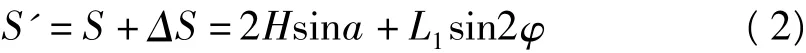
其中L1为光束反射点到光敏面上的距离。φ为平行块的转动角度，a为入射角，H为平行块移动距离，S为光斑移动距离。

由公式(2)可以看出，平行块的转动将会影响检测精度。为了保证测量精度，需要提高双平行簧片的抗扭特性，减小附加扭矩对检测精度的影响，虽然提高簧片的刚度可以提高其抗扭特性，但同时会导致传感器灵敏度降低。针对这一问题，我们通过建立双平行簧片传感器扭转效应的力学模型，找出提高其抗扭特性的方法

2 双平行簧片的扭转力学模型

图3为平行簧片传感器在扭矩作用下的受力分析，为建立理想状态下的理论力学模型，提出如下假设:双平行簧片结构扭转时，仅在平行簧片处产生柔性变形，平行块为刚体，不会产生变形。双平行簧片受到扭矩作用时，自由端平行块只有在平面内的转动，而不会发生偏斜，如图3所示，测量力由探针转移到平行块所产生的附加扭矩为:

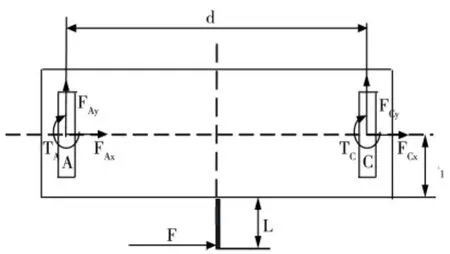
图3 双平行簧片机构受力分析图

图4 理想状态下的扭转变形

其中F为作用在探针上的测量力，L为探针长度，b1为自由端平行块厚度的一半。T为附加扭矩。

由图3可知，对于双平行簧片与平行块M相连一端A和C，不仅仅受到扭矩作用，还受到力的作用，列力学平衡方程为:

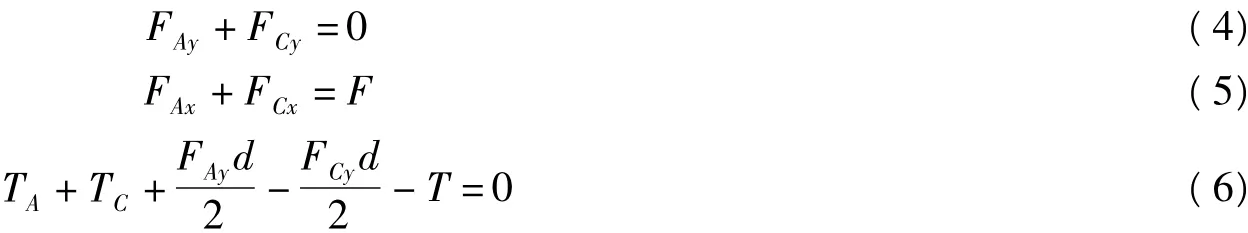
其中d为平行簧片间的间距，FAy和FCy为簧片AB和CD端部的剪力，FAx和FCx簧片AB和CD端部的轴向力，TA和TC簧片AB和CD端部的扭矩

如图4所示，双簧片材料为均匀的各项同性的材料，结构相同又平行对称，所以双簧片的在截面力和扭矩第作用下变化是相同的。簧片自由端A和C与平行块属刚性连接，所以簧片在平行块带动下发生扭转，且平行块的转动角与簧片的扭转角相同。设簧片的因受力变形产生的偏移量为w，因扭转变形产生的转角位Δβ，根据图4所示，可列写一个变形协调方程:

其中Δw簧片弯曲变形产生的偏移量为，Δβ为簧片扭转变形产生的扭转角与平行块转动角相同。

因为扭转就较小，所以方程可写为

结合协调方程，可以得到簧片的扭转力矩为

其中l为摩擦簧片的长度;E为杨氏模量;I为惯性矩;Ip为极惯性矩;G为切变模量;δ为矩形截面扭转系数。

3 ANSYS仿真分析

利用ANSYS软件对双平行簧片结构进行有限元分析。簧片的材料选为Fe:其弹性模量E=210Gpa;泊松比v=0.3，材料密度为7800Kg/m3，其中簧片的结构选为:长度l=0.05m，厚度 h=0.0001m，宽度 b=0.005m间距 d=0.014m，所受扭矩T=5×10-9N·M。改变其中任意因子，研究个因子对于扭转效应的影响，并讨论仿真结果与理论值的趋势和偏差。通过调整平行块的杨氏模量，将平行块定义为相对刚体，双平行簧片固定端施加固定约束。

由图5可知从有限元分析的仿真结果与理论值结果可以看出，平行块扭转角随着簧片的长度和扭矩的增加而增大，而且平行块转动角度与扭矩增长关系趋于线性。转动角随着簧片的宽度、厚度和平行簧片间距增加而减小，可以看出仿真结果和理论求解结果具有相同的趋势。由图5可知，对于平行簧片传感器的设计，可以在保证平行簧片平移刚度的情况下，通过改变双平行簧片间距，提高双簧片结构的抗扭特性。

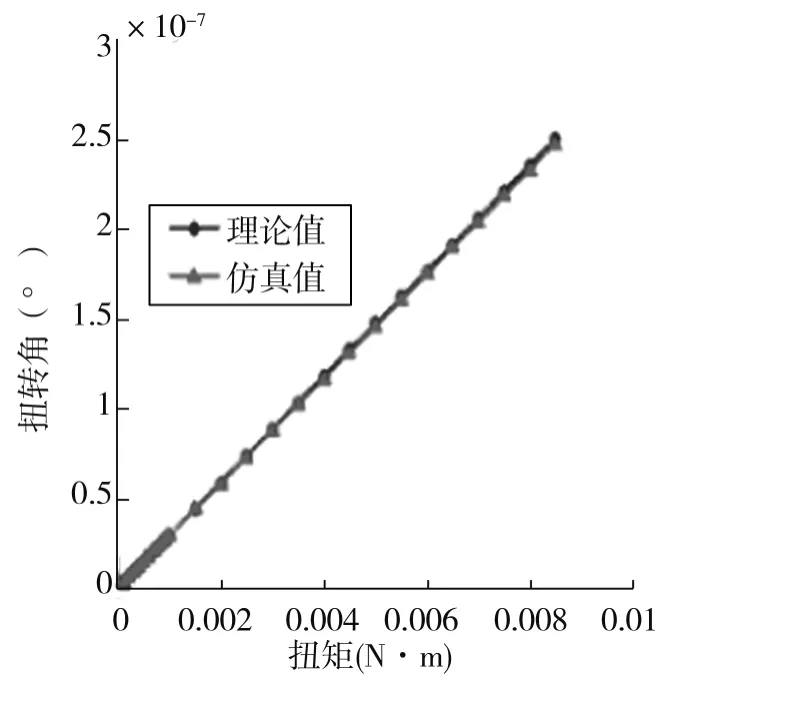
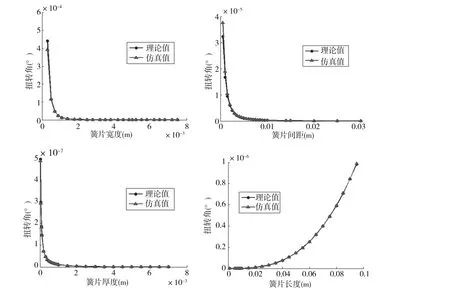
图5 各因素对理论值与仿真结果影响

4 结语

本文建立了双平行簧片结构扭转力学模型，并结合有限元数值仿真软件分双平行簧片各结构参数对其抗扭特性的影响，其结果表明:通过扭转力学模型获得结果与仿真结构相符，而且发现在不改变双平行簧片刚度的情况下，可以通过改变双平行簧片的间距提高其抗扭特性。

［1］周兆英，王晓浩，叶雄英，等.微型机电系统［J］.中国机械工程，2000(11):163-196.

［2］MOLLENHAUERO，AHMEDSI-U，SPILLERF，et al.High-precision positioning and measurement systems for microtribotesting［J］.Tri-botest，2006，12:189-199.

［3］余伟竟，肖晓天，刘莹，等.双悬臂梁结构弹性敏感元件的设计与应用［J］.仪表技术与传感器，2010(12):9-11.

［4］于正林，吴一辉，刘治华，等.光反射法微摩擦测试仪［J］.中国机械工程，2005(7):1299-1302.

［5］李一全，施庆永，于华东，等，微摩擦测试中双平行簧片结构弹性元件的设计［J］.仪表技术与传感器，2012(12):176-178.