基于层次分析法的市场营销专业实践教育效能评价

黄黎平

我们需要从不同角度为市场营销实践教育创造条件，为学生更好地参与教学实践活动提供良好的平台[1]675-677。以学生就业为前提，培养他们的理论知识和实际工作能力，是实践教育的根本任务，也是培养应用型、实践型和创新型人才的关键所在[2]129-130。我们不仅要加强实践教育，还需要从社会、学校、企业、教师和学生等方面，建立完善的市场营销专业实践教育效能的评价方法，对不同实践教育环节的效能进行评估。

实践教育活动的效能评价一直是市场营销教育改革领域亟待解决的热点、难点问题。随着市场营销专业人才培养模式改革的不断深入推进，必须对原有的实践教育效能评价体系进行相应的调整与改革，并提出行之有效的对策措施，以适应新形势下市场营销专业实践教育的需要。

一、市场营销专业实践教育效能的层次结构模型

在市场营销专业的实践教育效能研究中，本文希望通过评价和选择不同的实践教育项目，使其实践教育的综合效能最高，即决策目标是“合理规划实践教育环节，使市场营销专业实践教育综合效能最优”。为了实现这一目标，我们需要考虑四个准则，即虚拟实践教育、研究性实践教育、社会实践教育和职业实践教育。本文认为实践教育效能提升必须从情景演示、角色扮演、模拟实验、学年论文、案例研究、学生课题、毕业设计、社会调查、学科竞赛、假期实践、认知实习、企业实践、毕业实习和社会兼职十四个措施层予以完善。这些措施分属于前面四个准则。由此构成的实践教育效能层次结构模型如表1所示。

表1 运用层次分析法构建的实践教育效能结构模型指标

二、市场营销专业实践教育效能的调研数据

本文以调查问卷的形式对企业、教师和学生（包含在校和已毕业学生）进行调查，并形成如下调查结果：

（一）关于准则层的重要性数据

为了完成对市场营销专业实践教育效能的评价研究，本文根据市场调查态度测量法的量化理论，以调查问卷的形式对有校企合作关系的20家企业、相关高校市场营销专业的50名专业教师、市场营销专业本科毕业的学生进行了调查。同时，对实践教育效能的不同准则层、措施层两两比较重要性程度，按4、3、2、1的权重排序。通过计算，本文得到调查的重要性排序及汇总情况，分别见表2、表3、表4：

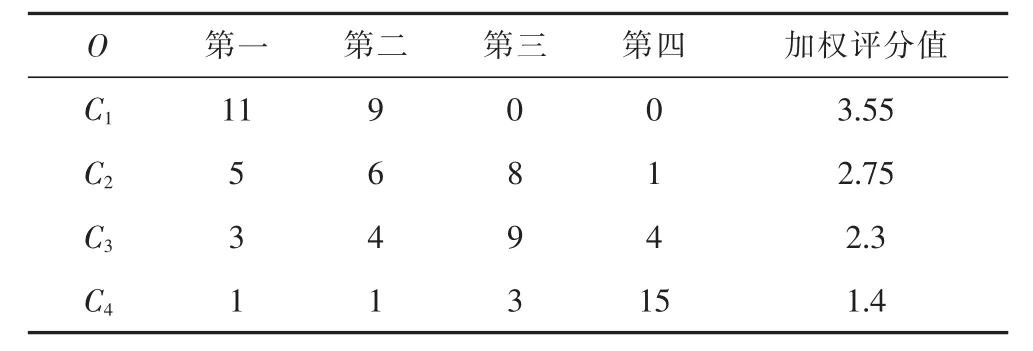
表2 标准层企业重要性排序汇总表

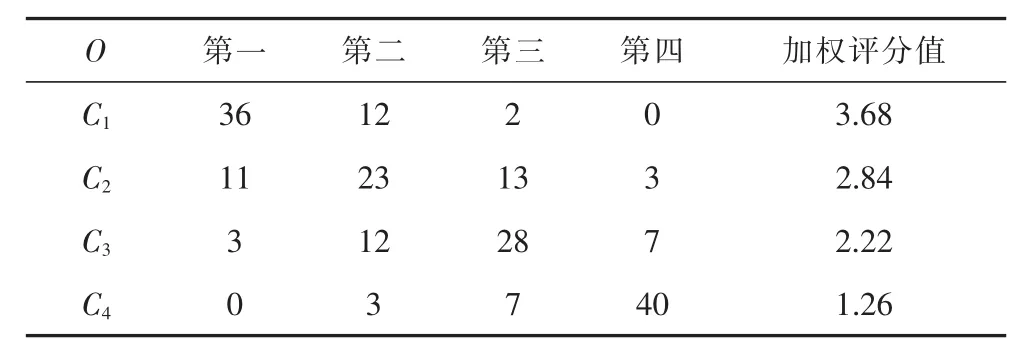
表3 标准层高校教师重要性排序汇总表

表4 标准层学生重要性排序汇总表

假设企业、高校教师和学生的平均评价分值的重要性是同等重要的，计算其综合平均加权分值为：职业实践教育3.72；社会实践教育2.873；研究性实践教育2.163；虚拟实践教育1.244。

（二）措施层的调查数据

根据标准层的方法，统计、计算措施层各项的综合加权评分值，得出以下结果。职业实践教育各项加权评分值分别是：企业实践的加权评分值为3.72；毕业实习的加权评分值为3.12；社会兼职的加权评分值为2.11；认知实习的加权评分值为1.05。社会实践教育各项加权评分值分别是：学科竞赛的加权评分值为2.36；社团活动的加权评分值为1.9；社会调研的加权评分值为1.74。研究性实践教育各项加权评分值分别是：毕业论文的加权评分值为3.06；学生课题的加权评分值为2.76；案例研究的加权评分值为2.38；学年论文的加权评分值为1.8。虚拟实践教育各项加权评分值分别是：模拟实验的加权评分值为2.54；角色扮演的加权评分值为1.85；情景演示的加权评分值为1.61。

三、市场营销专业实践教育效能的判断矩阵

本文对影响实践教育效能提升的不同准则层、措施层的重要性程度进行两两比较，按重要性程度赋值1-9，形成如下重要性标度表（见表5）：

根据调查访问的结果，我们对各项因素的评分值进行了两两比较，比值结果如下：

（一）标准层评分值的对比值

标准层评分值的对比值见表6：

表5 重要性标度表

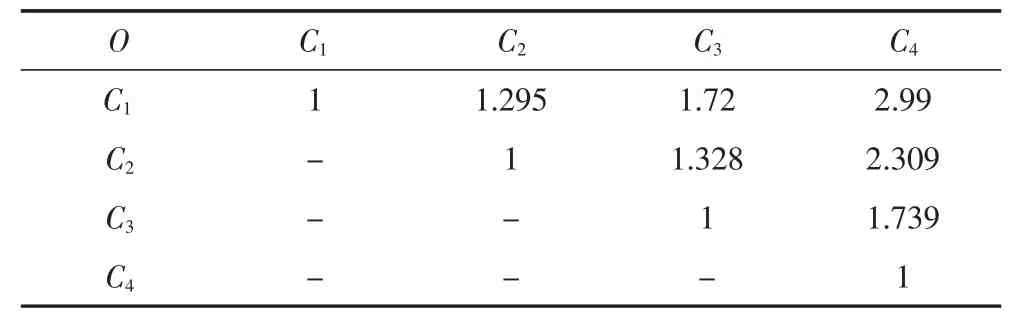
表6 标准层O-C评分值的对比值

根据对比值的结果进行重要性标度赋值，赋值范围如表7所示：

表7 重要性标度赋值的赋值范围设计

根据赋值构造的O-C判断矩阵见表8：

表8 O-C判断矩阵

在层次分析法中，我们需要对O-C的判断矩阵进行层次单排序，在此使用几何平均法。设对总目标O 的各准则 C1、C2、C3、C4的权重特征向量为，判断矩阵 O-C 的元素为 aij，其中 i，j=1，2，3，4。则其特征向量W0的分量计算公式为WCi=，其中 i=1，2，3，4。 然后对所得进行归一化处理， 得出 C1、C2、C3、C4的权重，按此，可以计算出C对于O的权重。计算结果为：

（二）措施层评分值的对比值

措施层评分值的对比值分别见表9、表10、表11、表 12：

表9 C1-P评分值的对比值

表10 C2-P评分值的对比值

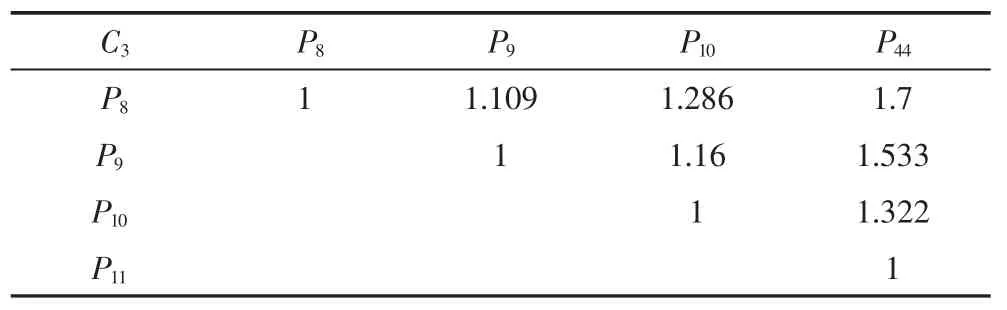
表11 C3-P评分值的对比值

根据对比值进行重要性赋值构造判断矩阵，见表 13、表 14、表 15、表 16：

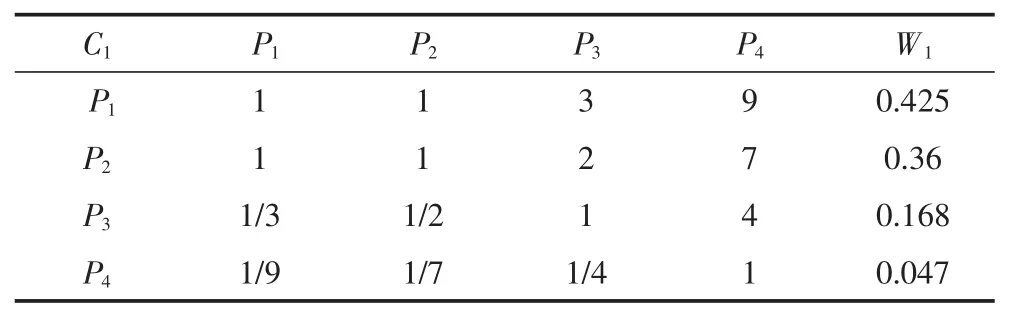
表13 C1-P判断矩阵

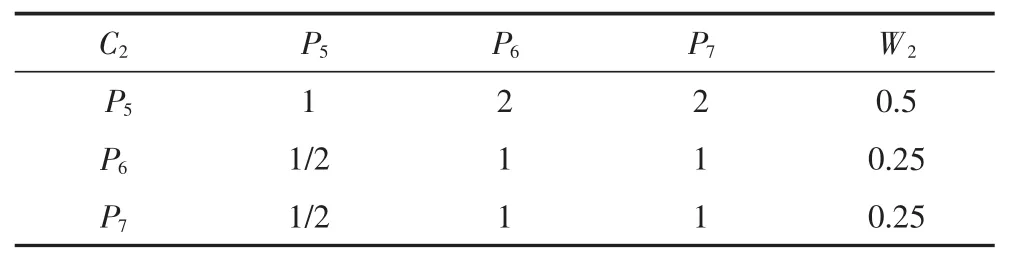
表14 C2-P判断矩阵

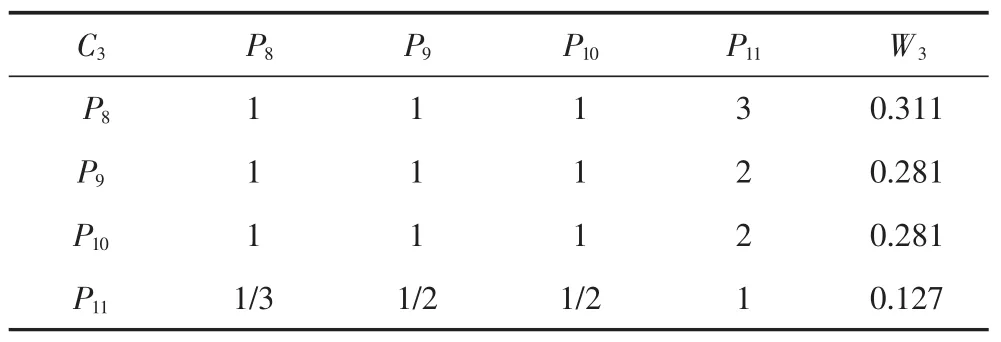
表15 C3-P判断矩阵

表16 C4-P判断矩阵

通过同标准层方法，计算出特征向量的分量并进行归一化，得到如下结果C1-P的分量及归一化：P1=2.28，WP1=0.425；P2=1.934，WP2=0.36；P3=0.904，WP3=0.168；P4=0.251，WP4=0.047。 C2-P 的分量及归一化：P5=1.587，WP5=0.5；P6=0.794，WP6=0.25；P7=0.794，WP7=0.25。 C3-P 的分量及归一化：P8=1.316，WP8=0.311；P9=1.189，WP9=0.281；P10=1.189，WP10=0.281；P11=0.537，WP11=0.127。 C4-P 的分量及归一化：P12=1.817，WP12=0.55；P13=0.794，WP13=0.24；P14=0.693，WP14=0.21。

四、一致性检验

以O-P判断矩阵为例，令判断矩阵用A表示，由上述计算得出 WO=（0.422 0.351 0.166 0.061），AWO=（1.6941.410.6560.247），λmax=1.006，一致性指标CI=-0.998，一致性比例CR=-1.11≤0.10。因此，可认为判断矩阵的一致性是可以接受的。同理可以验证判断矩阵 C1-P、C2-P、C3-P、C4-P的一致性都可以接受。

五、层次总排序及一致性检验

在以上计算中我们得出了一组元素对其上一层元素的权重向量，现在我们将这些向量进行合成以求得最低层方案对于目标的排序权重。得出的结果如下表17所示：

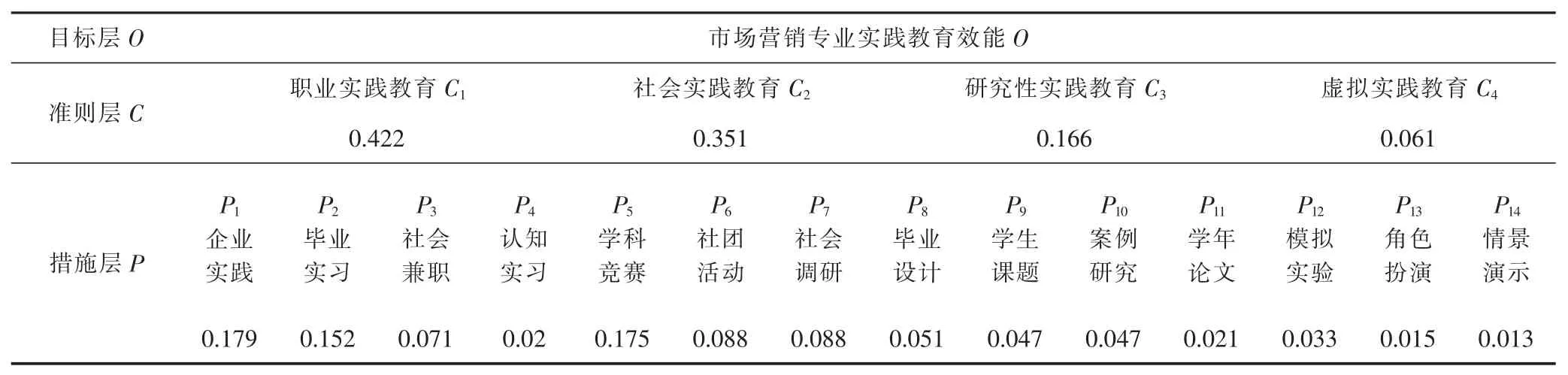
表17 基于层次分析法的市场营销专业实践教育效能权重比例汇总

六、层次分析模型结果的分析

根据以上计算，获得了市场营销专业实践教育不同环节对市场营销专业实践教育效能的权重比例。从数据的显示结果可以明显的分析出不同实践教育环节效能的精确结构示意图（如图1、图2）。

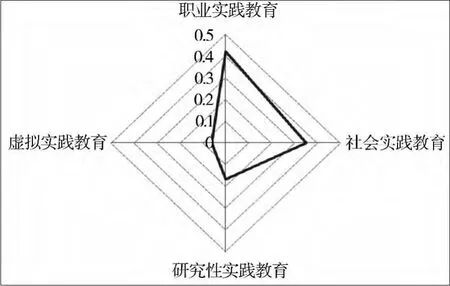
图1 基于层次分析法的实践教育效能标准层结构示意图

图2 基于层次分析法的实践教育效能措施层结构示意图

从实证分析的角度可以分析得出以下结论：

第一，从整体上来看，在标准层中，职业实践教育的效能最大，社会实践教育次之，虚拟实践教育效能最低；在措施层中，企业实践教育环节的效能最大，学科竞赛的实践教育效能次之，毕业实习环节在实践教育效能中居第三位，情景演示和角色扮演的实践教育效能最小。

第二，在职业实践教育上，企业实践教育环节最为重要，体现了我们在学生的实践教育活动中，必须要加强学生深入企业内部的实践活动，不能因为其实践教育成本较高而取消或减少这个环节。毕业实习这个环节也非常重要，我们应该加强对毕业实习的监管，以保证毕业实习取得预期的效果；认知实习的效能最低，我们应该予以改进完善。

第三，在社会实践教育上，学科竞赛的实践教育效能是有目共睹的。很多高校都积极组织学生参加各种类型的学科竞赛，已经说明了这个实践环节的重要性。然而，学科竞赛中教师的参与程度较低，对学生实践教育能力的培养还存在着局限性。究其症结，问题源于学校的管理制度存在缺陷，教师对学生的学科竞赛参与的积极性不高。

第四，在研究性实践教育上，毕业论文、学生课题和案例研究的实践教育效能比较均衡，但学年论文的效能偏低。我们从调查中发现学生对学年论文的普遍反映是教师的指导存在一定的问题，学生以应付为主，投入的精力较少。

第五，在虚拟实践教育上，角色扮演和情景演示的实践教育效能最低，学生普遍反映没有多大的实际意义和价值。模拟实验虽然要好些，但实践意义也不是很大。

七、总结

虽然本课题提出了运用层次分析法来评价实践教育的效能，但是我们在设计实践教育效能的标准层和措施层的时候难免存在不足，可能与部分高校实践教育环节的安排存在一定的差异。在调查的样本选择上，本文主要调查了重庆市内高校的教师和学生，调查的企业主要是以我校学生就业单位为主。样本的选择存在一定的主观性，制约了调查结果的应用范围。不同高校可以利用这个模型结合学校的实际情况对市场营销专业实践教育的效能进行评价，建立和完善提高市场营销专业实践教育效能的具体举措。这个评价模型还可以应用到其他专业领域进行实践教育效能的评价。

[1]张平.新建本科院校市场营销专业实践教学体系的构建[J].长春理工大学学报：社会科学版，2009（4）.

[2]周梅华，等.市场营销专业实践教学模式的构建与实施.黑龙江高教研究.2006（6）.