基于DTCWT和Laplace小波相关滤波的爆炸复合结构模态参数识别方法

思 悦，张周锁，成 玮，何正嘉，孔垂青

（1．西安交通大学 机械制造系统工程国家重点实验室，西安 710049；2．中国重型机械研究院股份公司，西安 710032）

爆炸复合结构已广泛应用于化工、石油、天然气、航空航天、汽车等行业和领域［1］，并且有巨大的工程需求。随着爆炸复合结构应用和需求的增加，对其结合状态（质量）的在线检测和评估的需求也日益迫切，依据结构模态参数的变化来识别和评估结构的状态和损伤是非常有效的结构在线检测和评估方法［2］。传统的结构模态参数识别方法要求同时测得激励和响应信号。然而在工程实际中，激励信号的测量往往比较困难，因此，仅根据结构响应信号进行模态参数识别的方法得到了发展［3］。

目前，根据结构振动响应信号辨识结构模态参数的方法有多种，如文献［3－5］中给出的直接根据输出信号识别模态参数的方法，但这些方法要求信号是平稳、均值为零的高斯分布，而且需要结合有效的剔除噪声信号的方法。爆炸复合结构由于两种材料结合面的存在，属于非均质材料结构，因而其动力学特性具有非线性，其动态响应信号具有非平稳性等特点，需要研究适用于非线性、非平稳信号的模态参数识别方法。Laplace小波是根据工程实际的需要构造出来的，具有与结构冲击响应信号类似的单边衰减性质，能够在强大噪声或其他干扰中准确捕捉到冲击响应信号，识别结构的固有频率和阻尼比等模态参数，对单阶模态具有很好的识别能力［6］。然而，当多阶模态混叠到一起时该方法难以精确识别各阶模态参数。双树复小波变换（DTCWT）的滤波器频响具有近似解析性，使其具有其他小波变换不具备的抗频带混叠特性［7－8］，可以将多模态混叠响应信号以较小的频带泄漏分解到各自独立的频带中，得到一组单模态分量。

本文结合DTCWT和Laplace小波的优势，提出一种基于DTCWT与Laplace小波相关滤波相结合的爆炸复合结构模态参数识别方法。文中首先介绍相关理论和算法；然后，构造仿真信号验证了DTCWT对多阶模态混叠响应信号有效分离的能力；最后，将本文所提方法应用于爆炸复合管模态参数提取。

1 模态参数识别原理

1．1 DTCWT基本原理［9－10］

经典离散小波变换由于存在频带混叠效应、平移变化性等缺点，限制了其在工程实践中的应用。双树复小波变换（DTCWT）是一种具有抗频带混叠和平移不变性等优点的小波变换方法。DTCWT的实部和虚部的小波变换分别满足完全重构条件，且实部和虚部的离散小波函数构成近似希尔伯特变换对，若ψh（t）和ψg（t）分别表示实部和虚部的实值小波，则DTCWT的复小波可表示为：

ψc（t）的频响特性具有近似解析表达式，即滤波器频响上几乎没有负频率成分，因此，DTCWT能减小频带混叠效应。

根据小波分析理论，双树复小波实部的小波系数与尺度系数（k）可以用内积运算表示为：

其中：l为尺度因子，J为分解层数。同理，可计算得到虚部的小波系数（k）和尺度系数m（k）。DTC-WT最终输出的分解系数是由实部和虚部各自的运算结果组合而成，如式（3）所示：

对分解后的小波系数重构时，利用式（4）将其他尺度小波系数置零，可实现对DTCWT分解后某一尺度小波系数的单支重构。

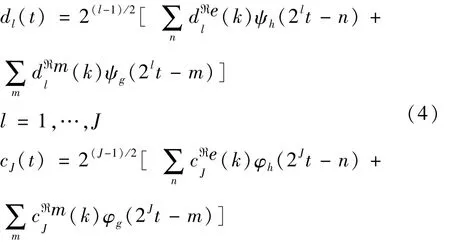
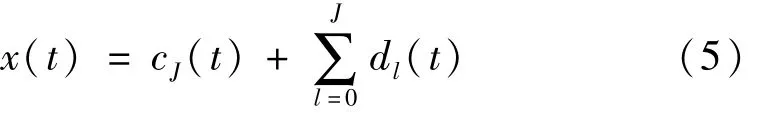
1．2 Laplace小波相关滤波的模态识别原理

Laplace小波是由 Freudinger等［11］构造出来的一种单边衰减的复指数小波，其解析表达式为：

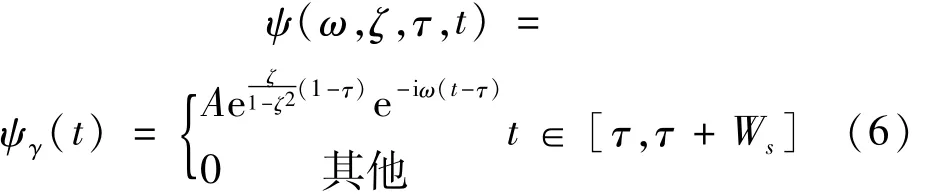
将振动响应信号x（t）进行DTCWT后，得到一组单模态分量，如式（5）所示：

上式中参数变量γ＝｛f，ζ，τ｝决定了小波的特性，其中：f∈R＋表示阻尼固有频率，决定了Laplace小波的振荡频率；ζ∈［0，1）R＋为黏滞阻尼比，ζ越大，La-place小波衰减越快；τ∈R为时间参数；系数A用来归一化小波函数，通常令A＝1；Ws表示小波紧支区间的宽度，一般不需显示表达。当 γ＝｛5，0．05，0｝，Ws＝5 s时，ψγ（t）的波形如图 1所示，可见 Re（ψγ（t））和lm（ψγ（t））与单自由度结构系统的自由衰减响应函数非常相似。

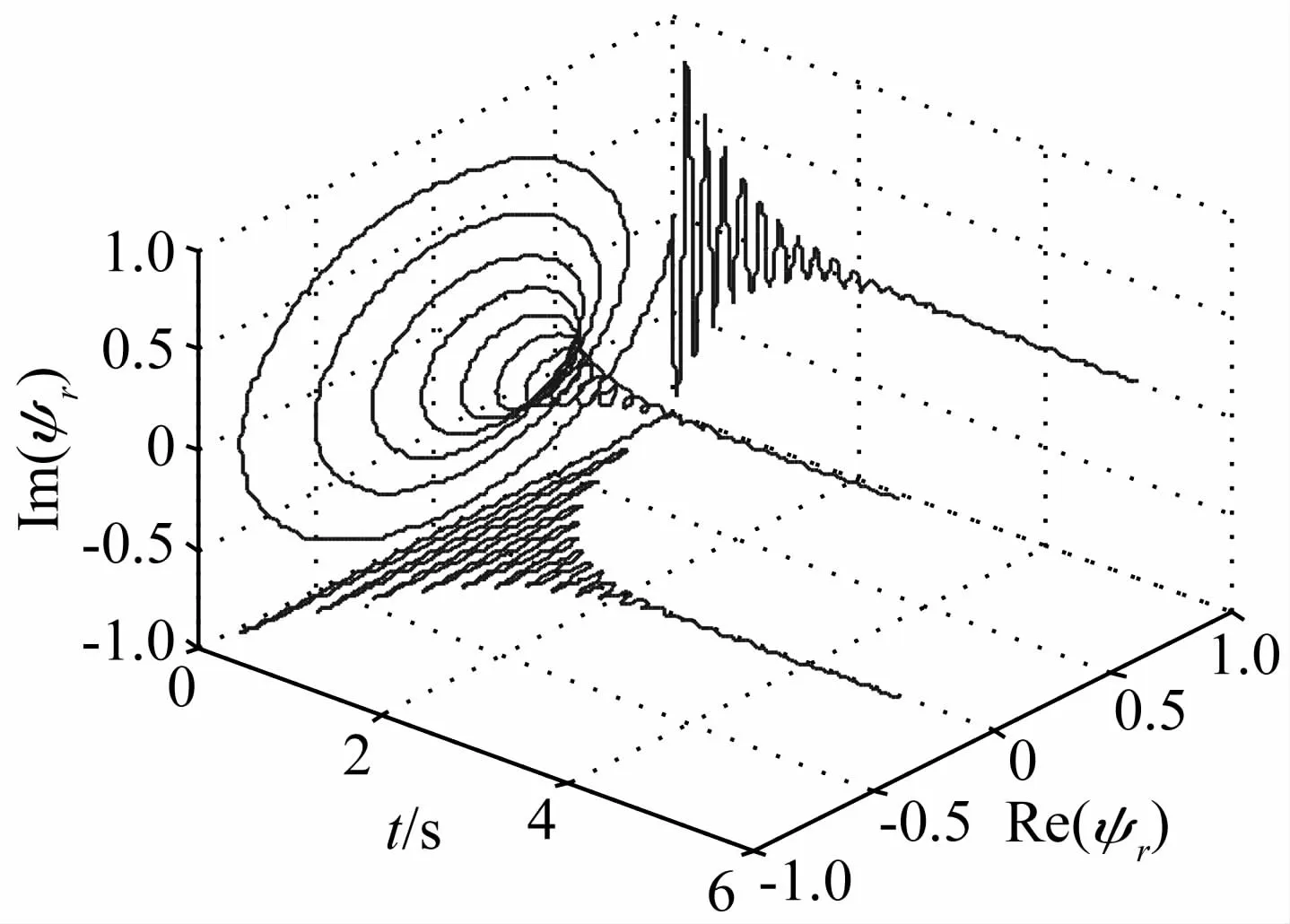
图1 Laplace小波图形Fig．1 Laplace wavelet

Laplace小波基函数库ψ是由一系列小波原子组成的，其表达式为：

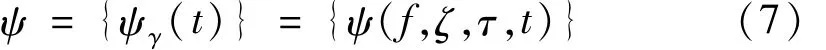
Laplace小波相关滤波法对结构模态参数的识别，是通过计算小波基函数库中小波原子 与待分析响应信号x（t）的内积，来衡量它们之间的相似性，其内积可以定义为：

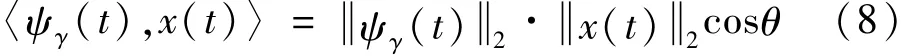
内积越大，两者越相似，通常用相关系数kγ来量化 和之间的相关程度，即：

其中标准化因子将 kγ限制在0～1之间，kγ越大，表示两者越相关，当 x（t）和 ψγ（t）完全线性相关时，相关系数kγ＝1。相关系数最大时刻对应的Laplace小波原子的频率f和阻尼比ζ，即为所分析响应信号x（t）的阻尼固有频率和黏滞阻尼比。

1．3 基于DTCWT和Laplace小波相关滤波模态识别原理

将DTCWT进行响应信号模态分离和Laplace小波相关滤波提取模态参数的优势相结合，提取爆炸复合结构模态参数。具体识别流程如图2所示。

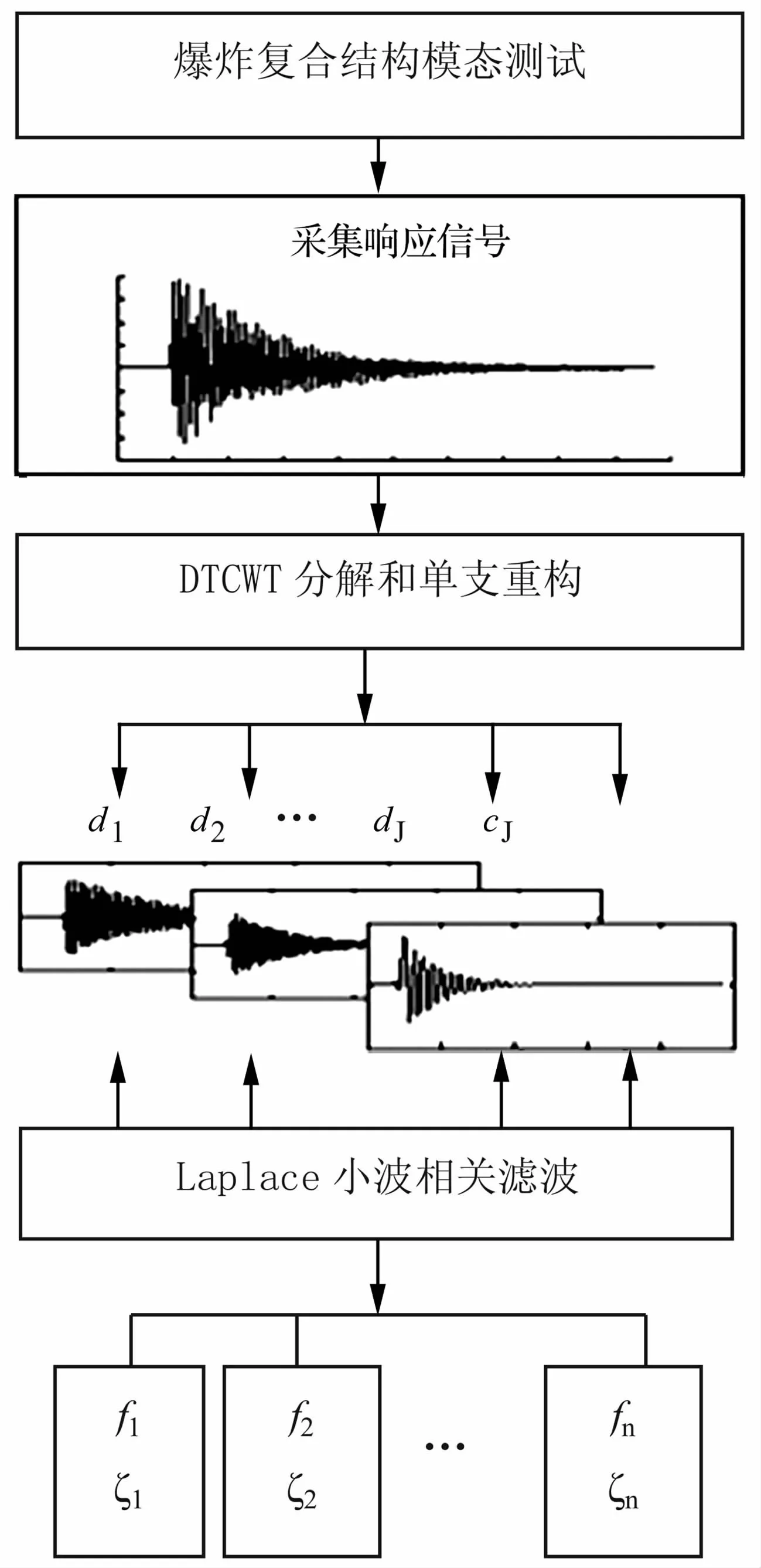
图2 基于DTCWT和Laplace小波的结构模态参数识别流程Fig．2 The flow chart of structural modal parameter identification based on DTCWT and Laplace wavelet

首先，采用DTCWT对原始响应信号 进行分解和重构，将x（t）中的各阶模态分量分解到各自独立的频带中，如式（5）所示。然后，构造Laplace小波基函数库，根据2．2节所述模态识别法分别对 dl（t）和 cJ（t）子频带信号进行Laplace小波相关滤波，提取各阶模态固有频率和阻尼比。

由于Laplace小波相关滤波法是利用基函数库中的小波原子逐一与待识别信号进行匹配，计算量大。为了提高计算速度，在定义小波基函数库时，先根据待识别信号的频谱中指示的频率，将基函数库中的频率因子f锁定在较小的范围内，再指定范围和间隔较大的阻尼比因子ζ，初步确定阻尼比大致所处的数量级。然后在相应的数量级上进行设置，以减少计算量。整个过程需要进行二次滤波。

2 DTCWT模态分离的仿真验证

为了验证双树复小波变换对多阶模态混叠响应信号模态分离的能力，构造一组多冲击成分组成的信号y（t），模拟结构的三阶模态响应信号。

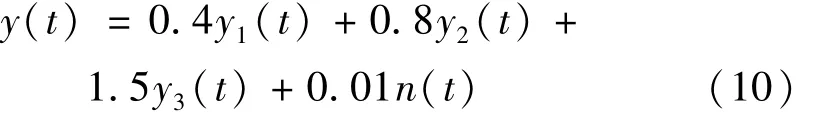
其中：yi（t）（i＝1，2，3）表示单阶模态冲击响应信号，其表达式如下所示：

式中：fi（i＝1，2，3）分别为：400 Hz，220 Hz，80 Hz；ζi（i＝1，2，3）分别为：0．004，0．02，0．04；n（t）表示白噪声信号，冲击发生时刻为t＝0．1 s，用1 024 Hz采样频率对响应信号y（t）离散化，采样点数为600。仿真信号y（t）及其组成成分的波形如图3所示。

图3 仿真信号及其组成成分Fig．3 The simulation signal and its components

利用DTCWT对此仿真信号进行2层分解，得到三个子频带信号，对三个子频带信号进行单支重构并做出对应的频谱，如图4所示。可见DTCWT可以很好地分离出各个冲击响应信号，各尺度中没有产生虚假频率成分，且受其他尺度能量泄漏影响很小。

利用DB8小波和EMD方法对仿真信号分解结果如图5和图6所示，图5中，虽然a2尺度中的频率成分可以分离出来，但是d1和d2尺度中均产生了290 Hz的虚假频率成分。图6中，IMF3尺度时域波形失真较严重，且频谱中各尺度产生58 Hz、175 Hz等较多幅值较大的虚假频率成分。

图4 仿真信号的DTCWT分解结果Fig．4 DTCWT decomposition results of the simulation signal

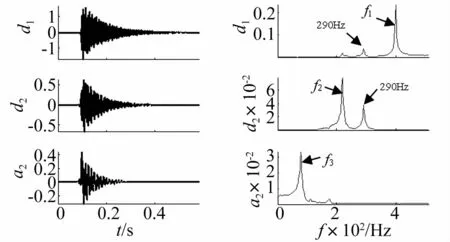
图5 仿真信号的DB8分解结果Fig．5 DB8 decomposition results of the simulation signal

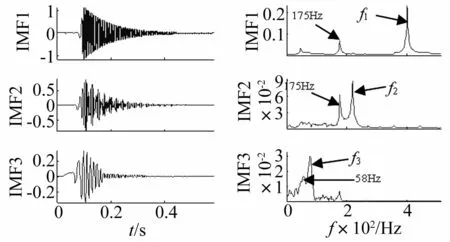
图6 仿真信号的EMD分解结果Fig．6 EMD decomposition results of the simulation signal

通过评估三种方法分解后的子带信号与原始信号相对应成分的相关系数，评估不同方法对混叠信号的分离能力。采用三种方法分解后的子带信号与原始信号相对应成分的相关系数如图7所示。根据相关函数的性质，相关系数越大表示子频带信号与原始信号相对应成分越接近。图7各子频带中，利用DTCWT法分解的子带信号与原始信号相对应成分相关系数最大，说明分解后的信号失真最小。综上述分析，由于DB8小波和EMD方法的频带混叠现象，产生了大量虚假频率成分，而DTCWT法具有良好的抗频带混叠能力，对多模态混叠信号的分离能力优于DB8小波和EMD等方法。

图7 子频带信号与原始信号相对应成分相关系数Fig7 Correlation coefficients between Sub-band signals with the components of original signal

3 实验验证

3．1 复合管振动响应信号采集

以不锈钢－碳钢爆炸复合管为研究对象，验证本文所述方法的有效性。搭建如图8所示的爆炸复合结构模态测试实验台，复合管长1 000 mm，外径89 mm，碳钢基管壁厚5 mm，不锈钢衬管壁厚2 mm。复合管悬挂，采用力锤在管道右端敲击作为激励源，用加速度传感器采集振动响应信号。

图8 爆炸复合管模态识别实验台Fig．8 Modal identification test bench of explosive cladding pipe

测试中，采样频率为10 240 Hz，采样点数为10 000，复合管振动响应信号如图9所示，采用本文所述方法根据该振动响应信号提取复合管模态参数。

图9 实验采集复合管振动响应数据Fig．9 Experimental vibration response data of the explosive cladding pipe

3．2 复合管模态识别

采用DTCWT对该响应信号进行3层分解，各子频带信号及其频谱如图10所示，该方法将振动响应信号中包含的前四阶模态信号分解到各自独立的频带中，没有产生虚假频率成分，只有d2频带中有一部分能量泄漏。

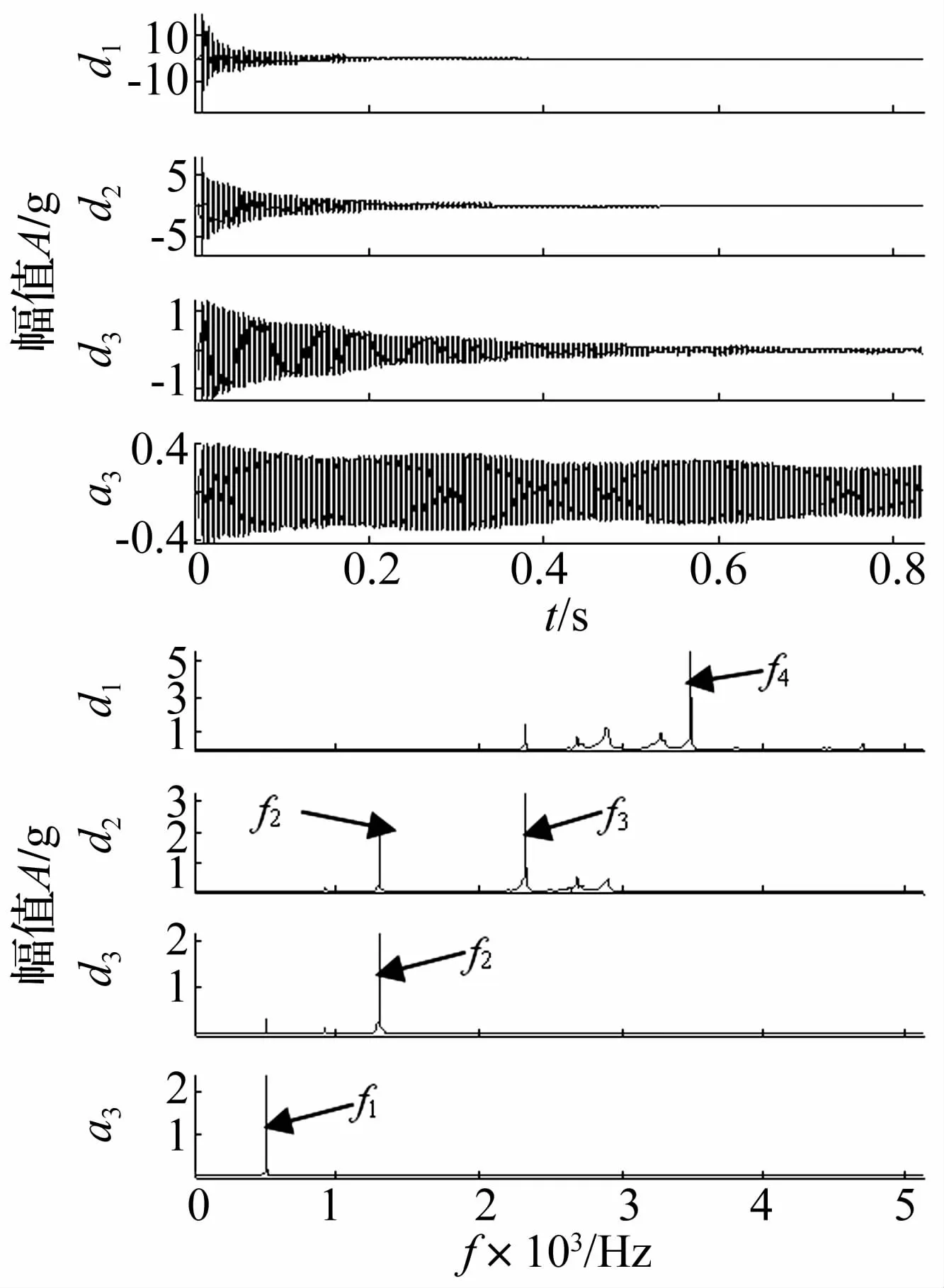
图10 实验数据的DTCWT分解结果及其频谱Fig．10 DTCWT decomposition results of experimental data and its spectrum

采用Laplace小波对经过DTCWT分解得到的各子频带信号进行相关滤波，提取出各阶模态参数，并与直接对原始信号进行Laplace小波相关滤波的结果对比，结果如表1所示。一般地，根据输入输出信号做频响函数分析可以精确识别结构模态参数，本文中采用模态分析软件Model Genius对根据激励和响应信号得到的频响函数分析，所得到的模态参数作为该复合管的模态参数的参考值。结果显示，本文方法识别的固有频率最大误差为0．022%，阻尼比最大误差为2．74%，识别误差小，精度高，与参考值最接近。直接相关滤波结果对固有频率识别精度较高，最大识别误差为0．14%，但是对阻尼比识别误差较大，最大误差为9．589%。可见，本文所提方法仅根据响应信号便可精确识别爆炸复合管前四阶模态参数。

4 工程应用

在某不锈钢－碳钢爆炸复合管生产线有两组编号为1和2的待检测爆炸复合管，两组管道尺寸相同（长度为9 600 mm，外径114 mm，基管壁厚8 mm，衬管壁厚3 mm），结合状态不同（爆炸焊接过程中所使用的炸药量不同），根据本文所提的模态参数识别法，提取两组管道的模态参数，从而区分不同状态的管道。从两组管道中各抽取一根管道，分别采集冲击振动响应数据，管道支撑方式为两端简支，采样频率为1 000 Hz，采样点数为8 200。图11和图12为采集到的振动响应信号。

表1 实验数据模态参数识别结果Tab．1 Modal parameter identification results of the experimental data

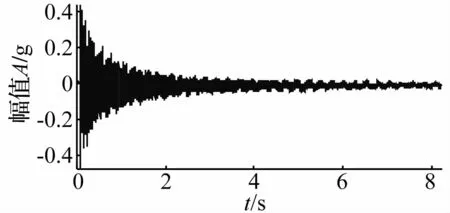
图11 1号复合管振动响应信号Fig．11 Vibration response signal of No．1pipe

图12 2号复合管振动响应信号Fig．12 Vibration response signal of No．2 pipe

利用本文方法提取该复合管模态参数。首先，采用DTCWT对两组振动响应信号分别进行3层分解，其中1号分解结果及其频谱如图13所示，可见DTCWT很好地将振动响应信号中包含的前四阶模态信号分解到各自独立的频带中，没有产生虚假频率成分，频带泄漏较小。然后，采用Laplace小波相关滤波法对各子频带信号进行模态提取，其中图13的d1子频带信号Laplace小波相关滤波结果如图14所示，可见该子带信号与Laplace小波相关系数最大值为1kr＝0．965，相关系数最大值时刻对应的固有频率f和阻尼比ζ就是该子带信号的固有频率和阻尼比。1号和2号爆炸复合管模态参数提取结果如表2所示，可见随着管道结合状态的变化，所有固有频率和阻尼比均有规律地变化，其中阻尼比变化比较均匀，而高阶固有频率变化较大，低阶变化很小，最小变化率只有0．06%，因此，精确识别模态参数对结构状态识别非常重要。本文所提方法仅利用振动响应信号便可精确识别爆炸复合管模态参数，为进一步根据模态参数变化识别爆炸复合管结合状态提供了依据。

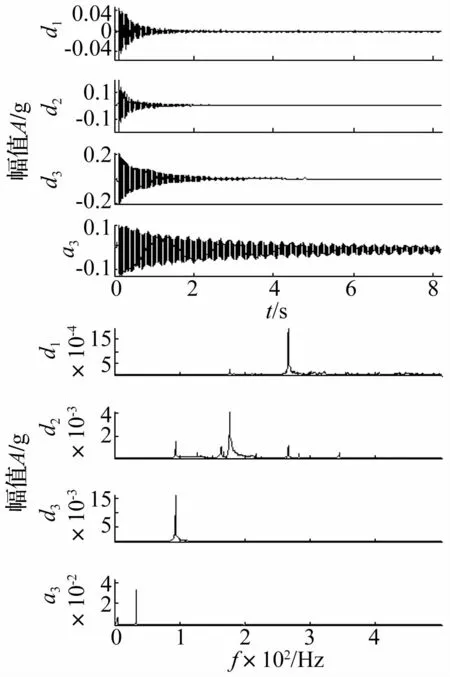
图13 复合管振动信号的DTCWT分解结果及其频谱Fig．13 DTCWT decomposition results of vibration signal and its spectrum

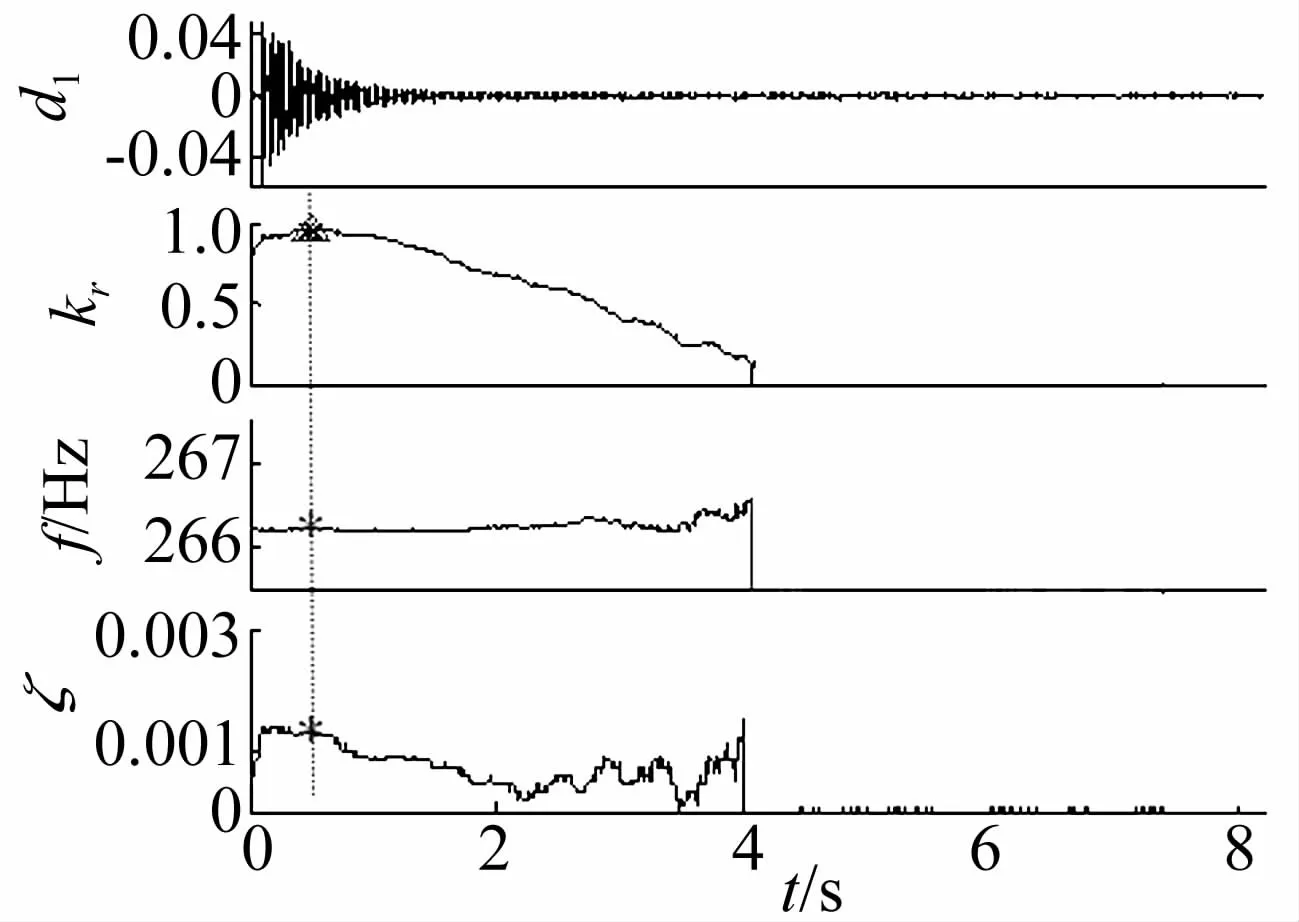
图14 d1子频带信号的Laplace小波相关滤波结果Fig．14 Laplace wavelet correlation filtering results of d1 sub-band signal

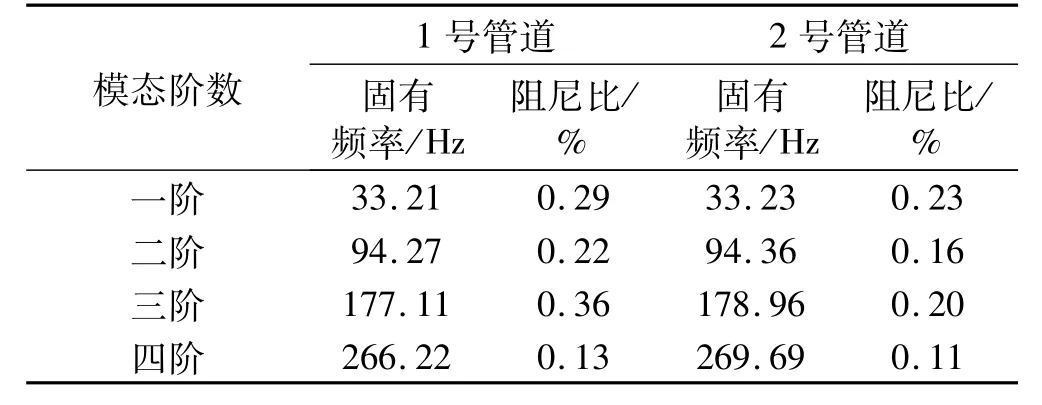
表2 1号和2号管道模态参数识别结果Tab．2 Modal parameter identification results of No．1and No．2 pipes

5 结 论

双树复小波滤波器组构成近似希尔伯特变换对，具有良好的抗频带混叠特性，能够将混叠信号以较小的能量泄漏分解到各自独立的子频带中。Laplace小波相关滤波法能够准确提取结构的单阶模态参数。本文将两者的优势相结合，提出了一种基于DTCWT和Laplace小波相关滤波的爆炸复合结构模态参数识别方法。

将该法应用于爆炸复合管模态参数提取实验中，仅根据振动响应信号成功提取了管道的前四阶模态参数。对比结果表明，该方法仅利用响应信号便可精确提取结构模态参数，提取精度优于Laplace小波直接相关滤波法。将该方法应用于生产线上不同结合状态的爆炸复合管识别，提取出了不同状态爆炸复合管的前四阶模态参数，成功区分了不同结合状态的复合管。为工程实际中爆炸复合结构状态检测奠定了基础。

［1］Cutter D．What youcan do with explosion welding［J］．Welding Journal，2006，7：39－43．

［2］李建国，赵亮，顾大鹏，等．桥梁结构模态参数识别方法综述［J］．城市道桥与防洪，2012（8）：159－162．LI Jian-guo， ZHAO Liang， GU Da-peng， et al．Summarization on modal parameter identification method of bridge structure［J］．Urban Bridge And Flood Cintrol，2012（8）：159－162．

［3］Zhang Y，Xu X．Modal parameter identification using response data only［J］．Journal of Sound and Vibration，2005，282（1）：367－380．

［4］张家滨，陈国平．利用响应数据识别模态参数的子空间在线递推算法［J］．振动工程学报，2009，22（1）：26－30．ZHANG Jia-bin， CHEN Guo-ping． An online subspace recursive method form odalidentificaion using output data［J］．Journal of Vibration Engineering，2009，22（1）：26－30．

［5］Zhou Wen-liang， Chelidze D． Generalized eigenvalue decomposition in time domain modal parameter identification［J］．Journal of Vibration and Acoustics，2008，130（1）：1－6．

［6］訾艳阳，李庆祥，何正嘉．Laplace小波相关滤波法与冲击响应提取［J］．振动工程学报，2003，16（1）：67－70．ZI Yan-yang，LI Qing-xiang，HE Zheng-jia．Extraction of impulse response based on correlation filtering method of lapalace wavelet［J］．Journal of Vibration Engineering，2003，16（1）：67－70．

［7］Selesnick I W，Baraniuk R G，Kingsbury N C．The dual-tree complex wavelet transform［J］．Signal Processing Magazine，IEEE，2005，22（6）：123－151．

［8］Barri A，Dooms A，Schelkens P．The near shift-invariance of the dual-tree complex wavelet transform revisited［J］．Journal of Mathematical Analysis and Applications，2012，389（2）：1303－1314．

［9］何正嘉，袁静，紫艳阳．机械故障诊断的内积变换原理与应用［M］．北京：科技出版社，2011：127－160．

［10］Wang Yan-xue，HE Zheng-jia，ZI Yan-yang．Enhancement of signal denoising and multiple fault signatures detecting in rotating machinery using dual-tree complex wavelet transform［J］．Mec hanical Systems and Signal Processing，2010，24（1）：119－137．

［11］Freudinger L C，Lind R，Brenner M J．Correlation filtering of modal dynamics using the Laplace wavelet［C］．1998：868－877．