悬挂式减振系统冲击动力学特性研究
2014-09-20赵笑春毕凤荣
赵笑春,毕凤荣
(1.天津大学 机械工程学院,天津 300072;2.天津大学 内燃机燃烧学国家重点实验室,天津 300072)
现代战争、抗震救灾等对精密仪器运输可靠性要求越来越高。据统计,美国侵朝战争期间,由于武器的包装、运输不当使武器装备损失高达45%。振动和冲击是导致设备在运输过程中损坏的两个主要动力学因素,研究系统冲击响应特性及其评价对设备安全运输有重大意义。Shi等[1]比较半正弦脉冲、三角脉冲和双线性脉冲波形对跌落测试仿真的影响。Daum[2]研究了产品疲劳损坏情况下冲击响应谱构建方法。缓冲包装主要采用填充瓦楞纸板、蜂窝纸板等衬垫缓冲法,但遇到剧烈冲击(空投、野战运输)仍会造成内装物损坏。悬挂式减振系统以弹簧作为减振缓冲元件将脆值较低的精密仪器、设备悬吊于外部容器内,使得产品在各个方向上都能得到缓冲保护[3]。
现有对悬挂式减振系统研究主要集中在单自由度、考虑关键部件的二自由度垂向振动、冲击模型分析,与实际情况存在误差。吴晓等[4-5]等讨论了悬挂弹簧减振系统自振以及在基础位移作用下的振动特性。王蕾等[6]详细探讨了矩形脉冲激励下相关因素对悬挂式减振系统冲击特性的影响。黄秀玲等[7]、王雷等[8]建立考虑关键部件的二自由度非线性系统模型,讨论了各因素对二维冲击谱和三维冲击谱的影响规律。王军等[9]提出了三维组合冲击谱新概念,用以描述多层堆码包装系统关键部件冲击特性。
本文以考虑平动和转动耦合的悬挂式减振系统为研究对象,建立系统无量纲冲击动力学方程,探讨质心位置、系统悬挂角、阻尼比、脉冲激励参数对系统冲击响应特性的影响规律。
1 系统冲击模型与方程无量纲化
考虑转动的悬挂式减振系统动力学模型如图1。坐标系原点建立在系统质心位置,质心沿坐标轴方向运动的位移为x、z,绕坐标轴转动的角位移为β。m为系统质量(不计缓冲元件质量),上下各有2个刚度系数k、原长l0的弹簧悬挂,φ0为系统悬挂角,c1、c2分别为x、z方向阻尼系数。对于悬挂式减振系统而言,根据简化的系统近似动力学方程[10],其力与变形的方程满足三次非线性关系:
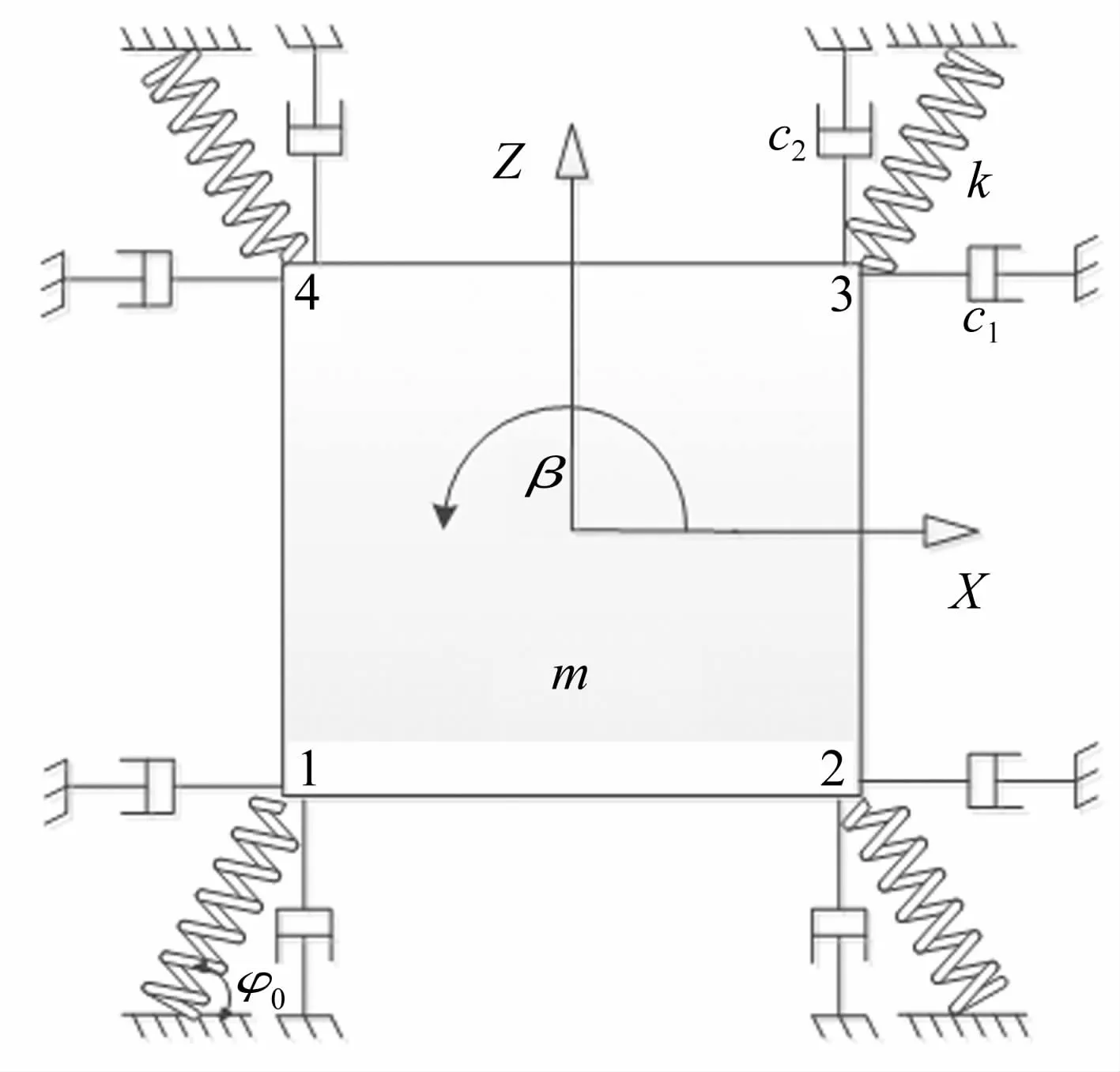
图1 悬挂式减振系统力学模型Fig.1 The mechanical model of suspension vibration reduction system
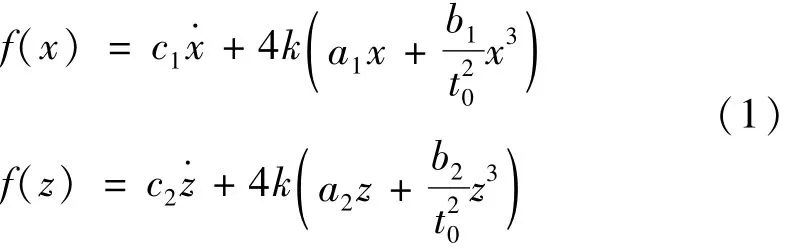
式中:f(x)、f(z)分别为系统沿 x、z方向的力与变形函数关系式;
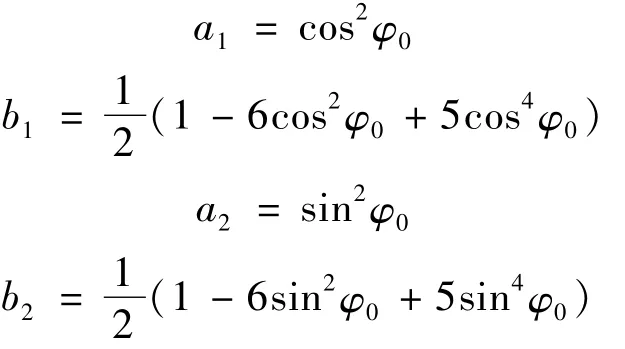
设系统受到基础半正弦脉冲激励,其数学表达式为:
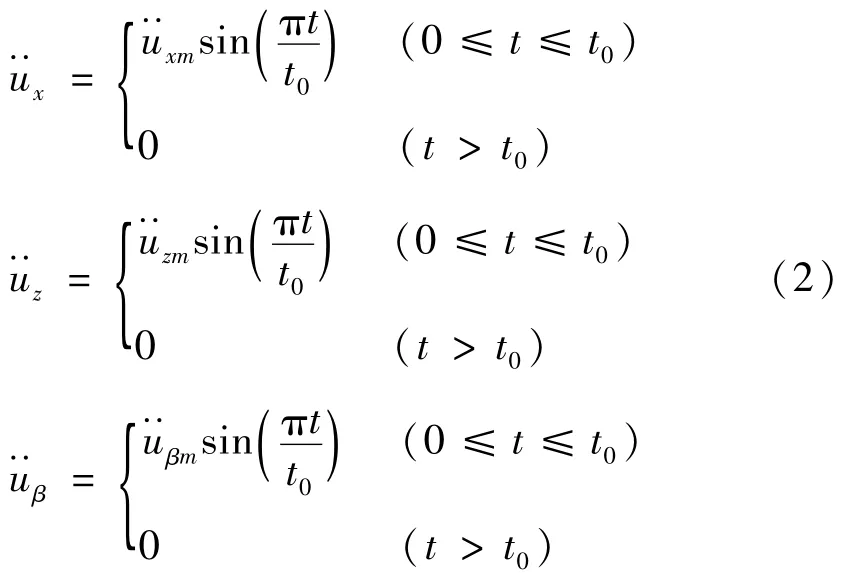
根据牛顿第二定律,可得到考虑转动的悬挂式减振系统运动微分方程:
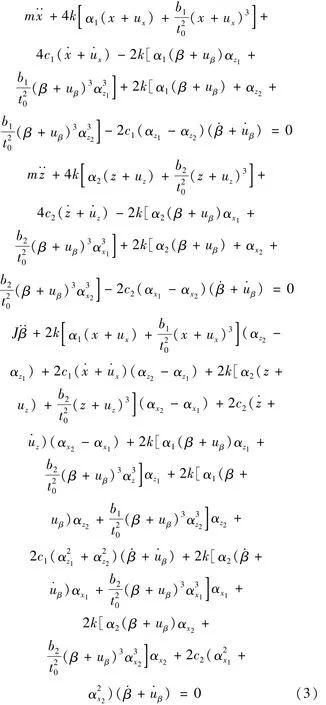
式中:J为系统的转动惯量;质心沿z轴与上、下端距离分别为 αz1、αz2;沿 x轴与左、右端距离分别为 αx1、αx2。
初始条件为:x(0)=z(0)=β(0)=0,(0)=(0)=(0)=0。对方程组(3)进行无量纲化处理,推得无量纲冲击动力学方程为:
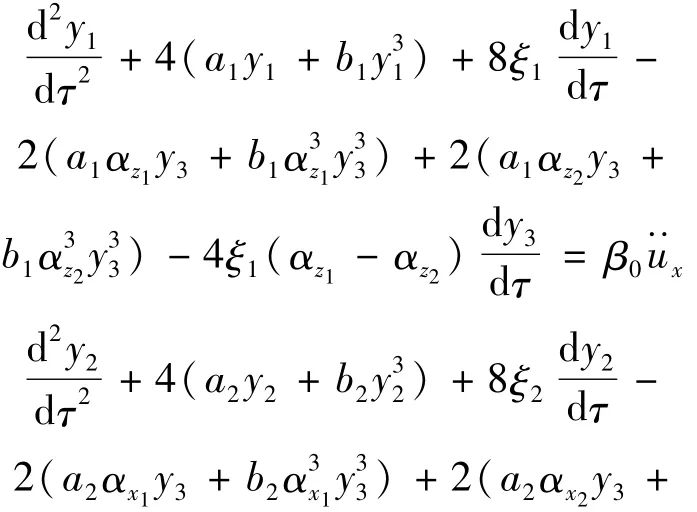

式中为系统无量纲参数;
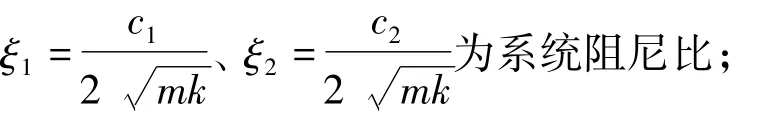
ω=系统频率参数,T=1
ω为系统周期参数;τ=为无量纲时间为无量纲脉冲激励时间;
R=为 系统转动半径,系统特征参数;
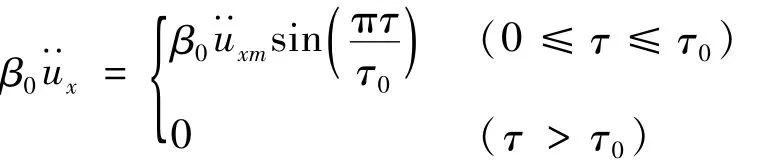

2 冲击响应计算及结果分析
由系统无量纲冲击动力学方程(4)可知,质心位置、系统悬挂角、阻尼比、无量纲脉冲激励时间和幅值等对方程的解都有影响。为探讨这些因素对系统冲击响应特性影响规律,用matlab编程采用龙格 -库塔法求解无量纲冲击动力学方程,以系统某一方向加速度响应峰值与对应方向脉冲激励幅值之比x,z,β))作为无量纲脉冲激励时间和其它因素的响应指标,建立三维冲击谱。
2.1 x、z方向脉冲激励下冲击响应谱
2.1.1 质心位置对冲击响应影响
当结构 参数0≤αx1≤0.8、αx2=0.8-αx1、0≤αz1≤ 0.26、αz2=0.26-αz1、R =0.26,脉冲激励ξ2=0.2,系统悬挂角φ0=60°时,系统冲击响应谱如图2。
由图2可知,质心在图1中2、4位置上,x、z方向冲击响应出现两次极大值,在4位置上转动方向上冲击响应最大;质心与系统几何中心重合时,z方向和转动方向冲击响应最小,在1、3附近位置上,x方向冲击响应最小。故系统2、4位置最容易遭到破坏,装载精密仪器、设备时应尽量使质心与系统几何中心重合。

图2 质心位置对冲击响应影响Fig.2 Effects of centroid position on shock response
2.1.2 系统悬挂角φ0对冲击响应影响
当结构参数αx1=0.2、αx2=0.6、αz1=0.1、αz2=0.16、R=0.26,脉冲激励尼比ξ =0.3、ξ =0.2,系统悬挂角45°12≤φ0≤90°时,系统冲击响应谱如图3。
由图3(a)可知,随悬挂角φ0增大,x方向冲击响应先减小后增大,φ0=70°时响应出现极小值;z方向和转动方向冲击响应增大,如图3(b)、3(c)。当系统仅受x方向脉冲激励时,悬挂角φ0越大,转动方向冲击响应越小,φ0≥70°时,响应趋于平缓幅值基本不变;当系统仅受z方向脉冲激励时,悬挂角φ0越大,转动方向冲击响应越大,且对z方向脉冲激励响应远大于对x方向脉冲激励响应,如图3(d)、3(e)。

图3 系统悬挂角φ0对冲击响应影响Fig.3 Effects of suspension angleφ0 of the system on shock response

图4 系统阻尼比ξ1对冲击响应影响Fig.4 Effect of damping ratioξ1 of the system on shock response
2.1.3 系统阻尼比 ξ1对冲击响应影响
当结构参数αx1=0.2、αx2=0.6、αz1=0.1、αz2=0.16、R=0.26,脉冲激励统悬挂角 φ =60°,阻尼比 0.1≤ ξ≤010.8,ξ2=0.2时,系统冲击响应谱如图4。
由图4(a)可知,随阻尼比ξ1增大,x方向冲击响应明显减小,但在ξ1≥0.5区域上对冲击响应影响较小;z方向冲击响应几乎不变,如图4(b);转动方向冲击响应减小,如图 4(c)。
2.1.4 脉冲激励幅值对冲击响应影响
当结构参数 αx1=0.2、αx2=0.6、αz1=0.1、αz2=0.16、R=0.26,系统悬挂角φ0=60°,阻尼比ξ1=0.3,ξ2=0.2,脉冲激励=0时,系统冲击响应谱如图分别表示为Xm、Zm分别表示为xm、zm、βm。
由图5可知,增大脉冲激励幅值,系统x、z方向冲击响应增大,且z方向响应峰值远大于x方向响应峰值;转动方向冲击响应也增大。
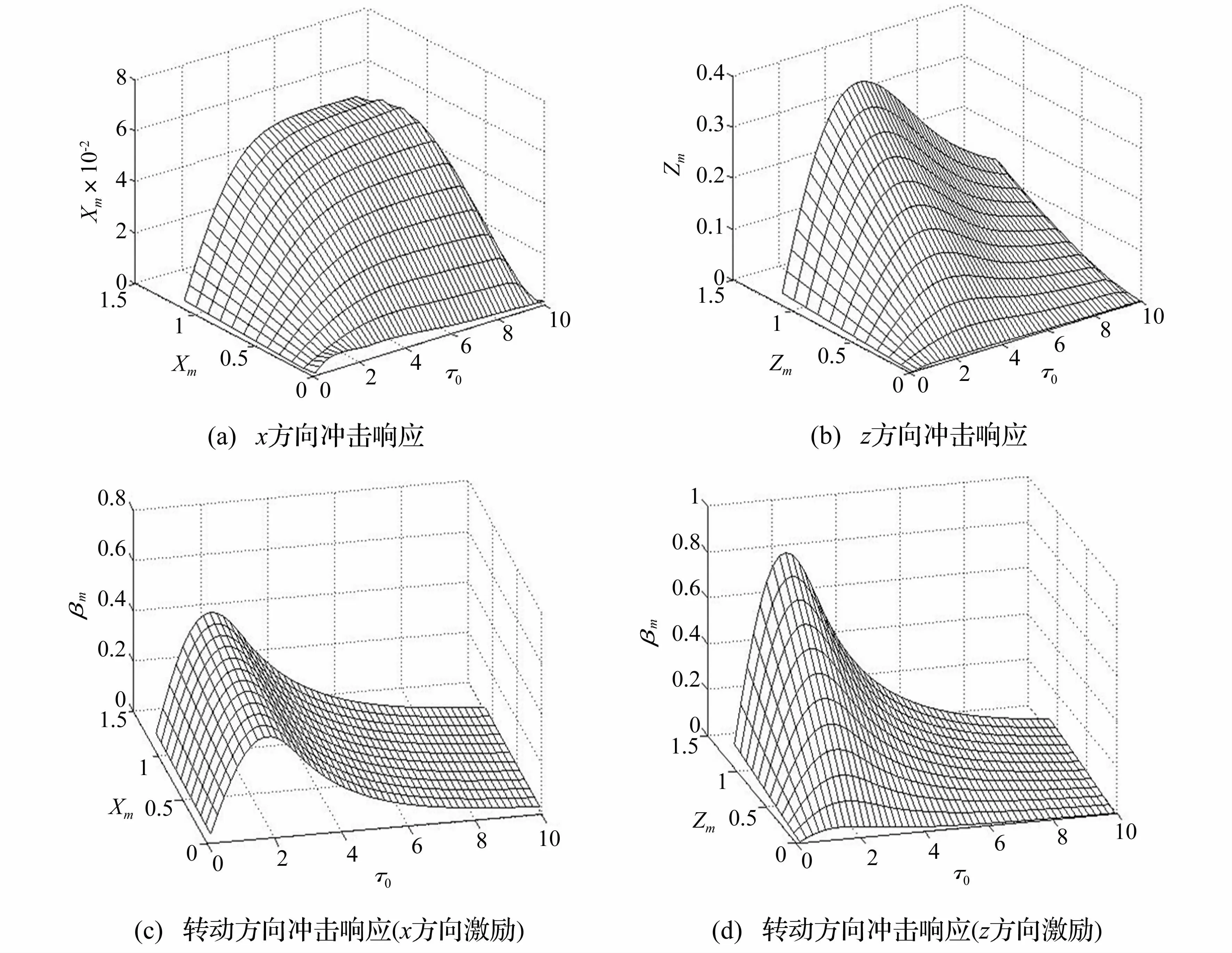
图5 脉冲激励幅值对冲击响应影响Fig.5 Effect of pulse excitationamplitudeon shock response

图6 系统悬挂角φ0对冲击响应的影响Fig.6 Effect of suspension angleφ0 of the system on shock response
2.2 转动方向脉冲激励下冲击响应谱
限于篇幅只讨论悬挂角φ0对冲击响应影响,其他参数可以用如上方法讨论,不另详述。当结构参数αx1=0.2、αx2=0.6、αz1=0.1、αz2=0.16、R=0.26,脉0.3、ξ2=0.2,系统悬挂角45°≤ φ0≤90°时,系统冲击响应谱如图6。由于x、z方向没有脉冲激励,故γx=
由图6可知,随悬挂角φ0增大,x方向冲击响应减小,但 φ0≥75°区域上响应几乎不变,仅与脉宽有关;z方向和转动方向冲击响应增大。
3 结 论
本文建立了半正弦脉冲激励下悬挂式减振系统冲击动力学方程,考虑实际存在的转动耦合和内部质量分布不均匀所导致的偏心情况,通过数值分析讨论了质心位置、系统悬挂角、阻尼比、无量纲脉冲激励幅值对系统冲击响应的影响规律,结果表明:
包装设备的质心位置应尽量与系统几何中心重合;受x、z方向脉冲激励时,系统x方向冲击响应在φ0=75°左右出现极小值,减小悬挂角φ0,系统z方向和转动方向冲击响应降低,且z方向与x方向脉冲激励相比可引起更大的转动方向冲击响应;增加阻尼比、降低脉冲激励幅值可明显抑制系统冲击响应。本文为悬挂式减振系统优化设计提供理论基础。
[1]Shi B J,Wang S,Shu D W,et al.Excitation pulse shape effects in drop test simulation of the actuator arm of a hard disk drive[J].Microsyst Technol,2006,12(4):299-305.
[2]Daum M P.Combining a fatigue model with a shock response spectrum algorithm[J].Journal of Testing and Evaluation,2004,32(5):1-5.
[3]彭国勋.运输包装[M].北京:印刷工业出版社,1999.
[4]吴晓,杨立军.悬挂弹簧几何非线性减振系统的固有振动特性[J].振动与冲击,2008,27(11):71-72.WU Xiao, YANG Li-jun.Natural vibration property of geometrically nonlinear vibration isolation system with suspension springs[J].Journal of Vibration and Shock,2008,27(11):71-72.
[5]吴晓,罗佑新,杨立军,等.基础位移作用下悬挂弹簧的非线性固有振动[J].北京理工大学学报,2009,29(12):1041-1043.WU Xiao,LUOYou-xin,YANGLi-jun,et al.Analysis on the vibration of shock absorber system with pendulum spring under foundation displacement excitation[J].Transactions of Beijing Institute of Technology,2009,29(12):1041-1043.
[6]王蕾,陈安军.矩形脉冲激励下悬挂式弹簧系统冲击特性的研究[J].振动与冲击,2012,31(11):142-144.WANG Lei,CHEN An-jun.Shock characteristics of a suspension spring system under action of a rectangular pulse[J].Journal of Vibration and Shock,2012,31(11):142-144.
[7]黄秀玲,王军,卢立新,等.三次非线性包装系统关键部件冲击响应影响因素分析[J].振动与冲击,2010,29(10):179-181.HUANG Xiu-ling,WANG Jun,LU Li-xin,et al.Factors influencing shock characteristics of a cubic nonlinear packaging system with critical component[J].Journal of Vibration and Shock,2010,29(10):179-181.
[8]王雷,王志伟,王军.三次非线性包装系统关键部件三维冲击谱研究[J].振动与冲击,2010,29(7):92-93.WANG Lei,WANG Zhi-wei, WANG Jun. Threedimensional shock spectra of a cubic nonlinear packaging system with critical component[J].Journal of Vibration and Shock,2010,29(7):92-93.
[9]王军,卢立新,王志伟.三次非线性多层堆码包装系统关键部件三维组合冲击谱研究[J].振动与冲击,2011,30(1):188-190.WANGJun,LU Li-xin,WANGZhi-wei.3-D combined shock response spectrum of a cubic nonlinear stacked packaging system with critical components[J].Journal of Vibration and Shock,2011,30(1):188-190.
[10]王蕾.悬挂式缓冲包装系统动力学性能的研究[D].无锡市:江南大学,2012.
