地铁浮置式轨道引起地表振动响应解析预测模型研究

吴宗臻，刘维宁，马龙祥，王文斌

（1．北京交通大学 土木建筑工程学院，北京 100044；2．铁科院（北京）工程咨询有限公司，北京 100081）

城市轨道交通的飞速发展在改善城市交通拥堵的同时，也引起了越来越严重的环境振动问题［1］。为了降低地铁列车运行对周围环境的振动影响，各类减振产品广泛应用于地铁各线的减振区段。其中浮置式轨道具有固有频率低，减振效果好，不影响轮轨工作性能等优点，主要结构型式有钢弹簧浮置板轨道［2］、橡胶浮置板式轨道［3］（浮置式道床轨道）和梯式轨枕轨道［4］（浮置式轨枕轨道）等。我国现行《环境影响评价技术导则——城市轨道交通》［5］推荐采用统一的经验链式公式作为环境振动预测计算方法，该方法简单快捷，普适性强，（但是精度较低且无法在频域内进行定量预测。尤其对于采用浮置式轨道的环境振动敏感区段，往往对振动频谱有特殊的要求，规范推荐的Z振级预测公式已经不能满足实际应用要求。而且随着城市轨道交通路网越来越密集，沿线的敏感目标也会大量增加，现有的地铁环境振动的频域内解析和数值预测方法往往计算周期较长，无法适用于同时精确高效的预测地铁沿线多个敏感目标的环境振动［6］。因此，环境振动评价亟须要一种满足频域预测精度要求且快速高效的预测方法进行辅助决策。

针对地铁环境振动多点同步快速预测问题，提出了一种适用于区间地铁引起环境振动的频域快速预测模型，将浮置式轨道环境振动问题转化为通过浮置式轨道模型［7］求解作用于基底的频域力群和通过地表振动响应的三维Green函数［8］求解土层频响函数群，然后将两者进行频域内复数叠加运算得出地表的振动响应。采用本模型预测了北京地铁4号线浮置板区间地表振动响应，并与现场地表振动实测数据进行对比分析，验证了该模型的可行性和准确性。本模型具有较高的预测精度和较快的计算速度，可用于预测地铁建设设计阶段的地铁运行引起的环境振动的加速度时程，频谱，1／3倍频程与Z振级。

1 模型基本原理及预测流程

对于地铁列车引起的振动传播系统，国内外学者通常将其视为线弹性系统，对于土层也多是将其简化为水平成层线弹性体［9－10］。实测表明，地铁运行引起的环境振动的量级较小，土层处于弹性应变阶段［11］。因此，本模型将土层系统简化为水平成层弹性体。

对于线弹性的系统，任意两点间的振动传递规律是系统的固有特性，不同频率处的振动传递性质不因振源输入的不同而改变。地表振动响应Green函数描述了在半无限空间成层土体内部的单位脉冲激励作用下的地表振动响应，通过Green函数可以求得土体内部某点作用一垂向单位脉冲荷载的地表测点处的振动响应，称之为土层振动频响函数。本预测模型即将车轨模型作用于基底的频域力与该点处频率响应函数进行运算，从而利用线弹性系统振动传递特性来的达到预测地表振动的目的。

整个预测模型实现过程分为三个主要步骤：

第一步，本预测模型通过解析的方法求解出浮置式轨道系统作用于基底的频域力群F＾n（ω），将列车运行的复杂时空效应转化为固定系列点荷载输入，如图1所示。

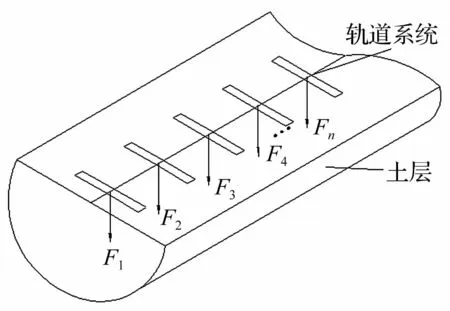
图1 轨道模型求解的基底频域力群Fig．1 Forces on base calculated by track model

第二步，采用成层土体三维Green函数求解出基底频域力群（ω）作用点处到地表预测点处的振动频响函数群 Hn（ω）。

第三步，将对应位置处的频域力和频响函数进行复数相乘运算得到单个固定力输入的地表预测点的振动响应（ω）×Hi（ω）。最后在频域内进行复数叠加运算得出频域力群（ω）作用下地表预测点处的振动响应（ω），即为地铁列车经过浮置式轨道引起的地表响应，如式（1）所示。

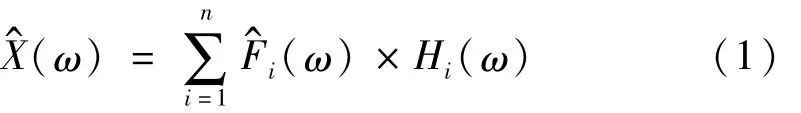
其中：n为计算的基底频率力的数目，ω为圆频率，符号“＾”代表频域内的物理量。

预测模型的基本流程如图2所示。

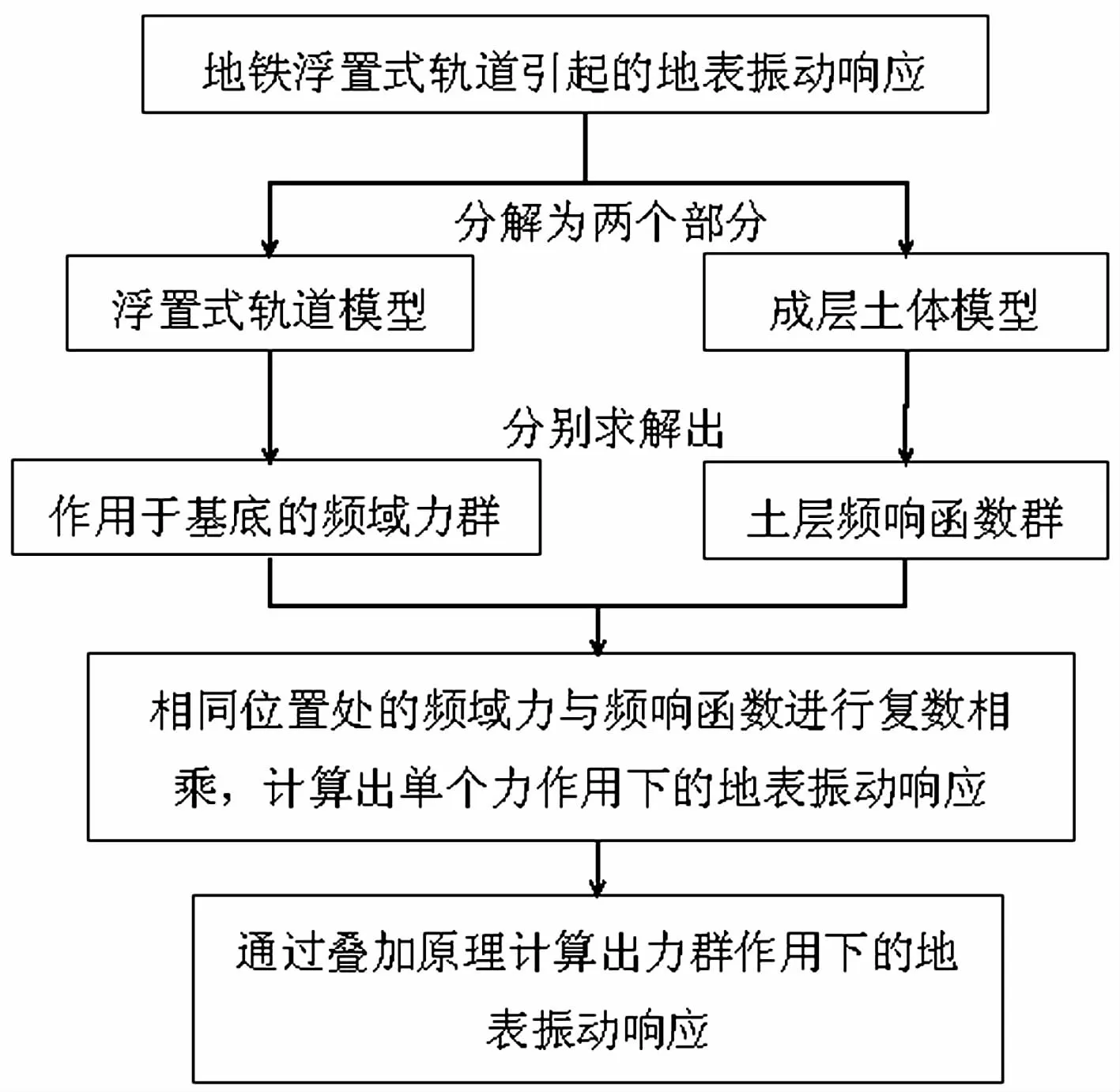
图2 预测模型流程图Fig．2 Flow chart of prediction model

本模型将地铁列车运行的时空荷载输入，变换到与时间无关的频域内进行求解，整个计算过程都是在频域内进行的复数运算，频域力、频响函数以及最终预测结果都包含了幅值和相位全部信息。通过分解及转化的思想可以快速的得到地铁列车在浮置式轨道上运行作用下的环境振动响应。

2 预测模型解析解

2．1 浮置式轨道模型基底力群的求解

为了准确地求解出浮置式轨道系统作用于隧道基底的频域力 F＾n（ω），需要构建高精度的车轨耦合模型［7，12］（图 3）。模型中，车辆采用 6节编组，每节车厢有4个轮对、2个转向架、1个车体，都简化为刚体，一系、二系弹簧简化为弹簧阻尼元件。轨道系统为以一个浮置板长为周期的无限长结构，其中，将钢轨简化为离散点支撑的无限长欧拉梁，浮置板简化为离散点支撑的有限长欧拉梁，扣件及隔振器简化为弹簧阻尼单元。

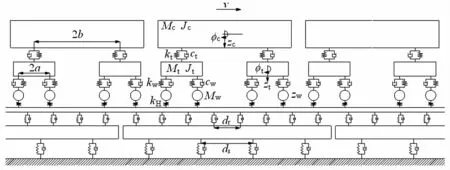
图3 浮置式轨道车轨耦合模型Fig．3 Coupled train-track model of floating-type track

在求解模型的过程中，轮轨激振形式采用移动荷载状态激振（车轮在具有不平顺的轨道结构上向前移动）［12］，而非传统的定点荷载状态激振（车轮不动，轮轨表面不平顺的激励带反向移动）。

模型的基本求解思路如下：

（1）在采用移动荷载状态激振的前提下，将轨道不平顺表示成系列三角函数的叠加，在单一频率成分的不平顺下，求解对应频率的轮对柔度矩阵及轨道结构上轮轨接触点的柔度矩阵，而后耦合车辆系统及轨道系统，求得相应频率成分的动态轮轨激励力。

（2）将考虑的所有频率成分不平顺引起的动态轮轨激励力计算出来并进行叠加，将总轮轨力表示成一系列具有不同频率成分的简谐力的叠加。

（3）求解移动简谐荷载作用下的浮置式轨道系统的动力响应。

（4）将求解出的轮轨力（系列简谐力的叠加形式）带入简谐荷载作用下的浮置式轨道模型的动力响应解答中，从而达到车辆响应及轨道响应的求解，进而得到基底频域力群。

文献［12］给出了在移动荷载状态激振下的轮对相互影响系数的求解方法，这是求解车轨耦合模型的轮轨力的基础。文献［7］给出了一种考虑周期性结构基本性质的采用模态叠加技术的数值方法，可以精确快速的求解出浮置式轨道在移动谐振荷载作用下的动力响应。

基于这些成果形成程序STFSTI，计算得到车轨模型动力响应及基底频域力群F＾n（ω）（图4）。具体的理论推导过程可以查阅相关参考文献，此处不再赘述。

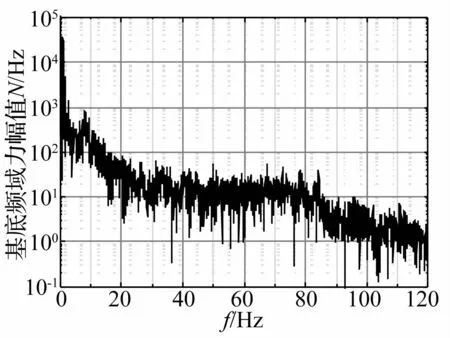
图4 典型基底频域力Fig．4 Typical force on base in frequency domain

2．2 土层频响函数群的求解

将土层简化为水平成层的半无限空间弹性体，每个土层均为各向同性的连续弹性介质（图5）。土体Green函数［8］表征了在土体内部某一坐标方向上施加一个单位脉冲荷载，在任意一点处产生的振动响应。土层内部脉冲激励作用下的地表测点处的频响函数群可以通过求解水平成层土体表面Green函数得到。

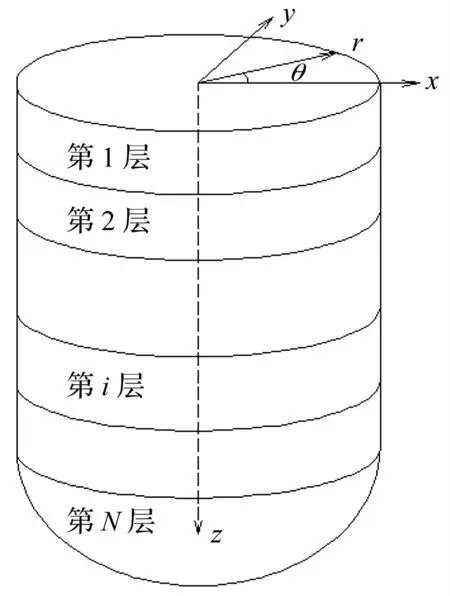
图5 成层半空间土体模型Fig．5 Model of layered half-space soil

采用直接刚度法［13］求解土体Green函数的基本思路如下：

（1）通过积分变换把时间－空间域内的波动方程转化到频率－波数域，之后在频率－波数域内推导出每层土体交界面上的位移和面力。

（2）建立每层土体的刚度矩阵（这个刚度矩阵称为单元刚度矩阵），即通过刚度矩阵可以建立每层土体上下表面上的面力和位移之间的平衡方程。

（3）把各层土体的单元刚度矩阵集总成一个总刚度矩阵，并建立一个总的平衡方程，解这个平衡方程，可以得到各个土层交界面上的位移，最后通过形函数可以求得每个土层内部的位移和面力。

（4）在土体内部施加垂向脉冲激励，将垂向脉冲荷载带入总平衡方程，根据Green函数的定义，此时所求得的土层内部的位移和面力即为土体的Green函数。地表的Green函数解答即为本文需要的土层频响函数群 Hn（ω）。

3 预测模型的实测验证

3．1 现场振动加速度实测

为了验证本预测模型的适用性，选取北京地铁钢弹簧浮置板区间进行振源加速度测试，在钢轨、道床及隧道壁上布置传感器，测点布置如图6所示。

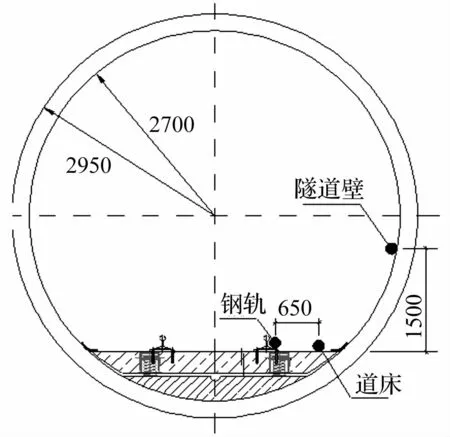
图6 隧道内加速度传感器布置图Fig．6 Lacations of sensors in tunnel

另外选取北京地铁4号线北大东门区间的钢弹簧浮置板区段进行地表振动加速度测试，地表测点的位置为距离地铁隧道中心线水平距离30 m处，隧道、土层及地表测点位置关系如图7所示。

图7 隧道及土层关系图Fig．7 Distribution of tunnel and soil

振动测试采用INV3018C型24位高精度数据采集仪以及 Lance系列高精度压电式加速度传感器。INV3018C型24位高精度数据采集仪采用24位ΔΣ方式的AD转换器，结合了最新FPGA和DSP技术，可8个通道并行处理，单个通道最高采样频率51．2 kHz，动态范围120 dB。数据采集及分析软件为DASP V10。

3．2 浮置板轨道振动加速度验证

将前文构建的浮置式轨道模型编制Matlab程序进行计算，参数采用钢弹簧浮置板轨道（FST）实际参数，如表1所示。

图8～图9为浮置板上的振动加速度频谱和1／3倍频程谱的实测值与计算值的对比。可以看出，计算值与实测值量值相当，变化趋势相同。结果表明浮置式轨道模型构建及求解过程科学合理，采用其求解出的频域力群是准确可信的。

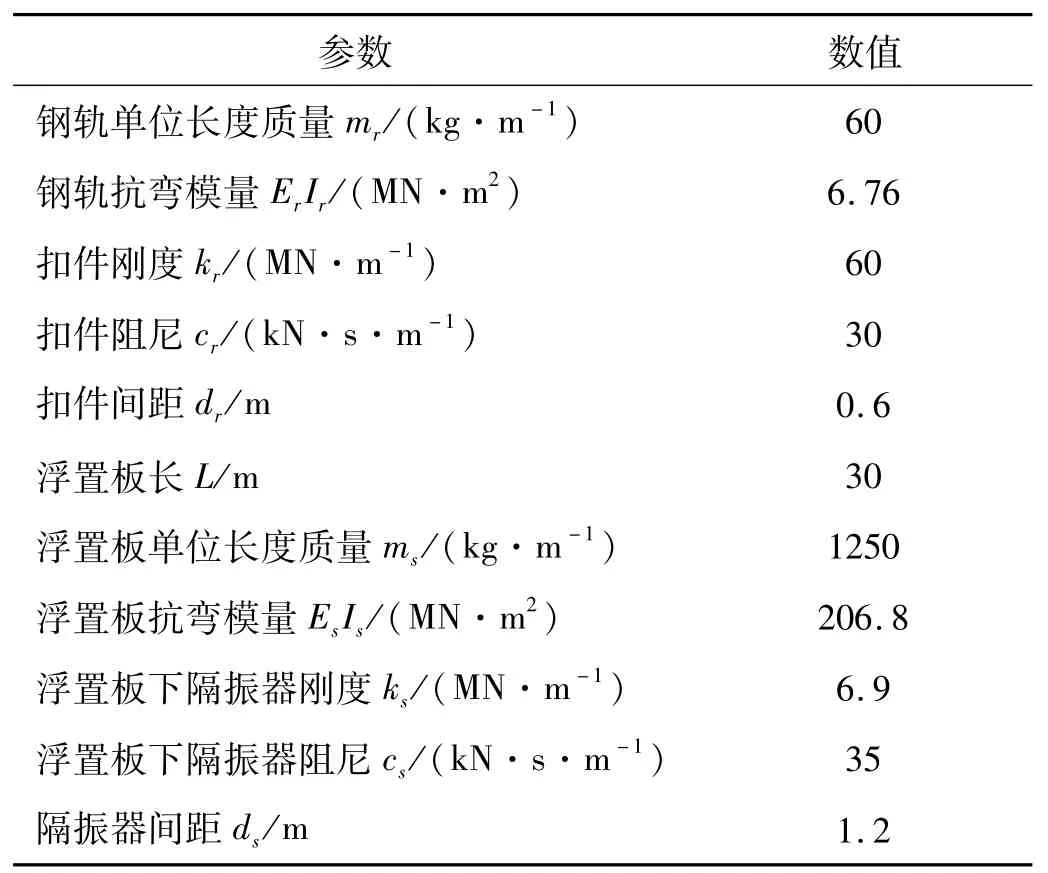
表1 轨道参数Tab．1 Track parameters

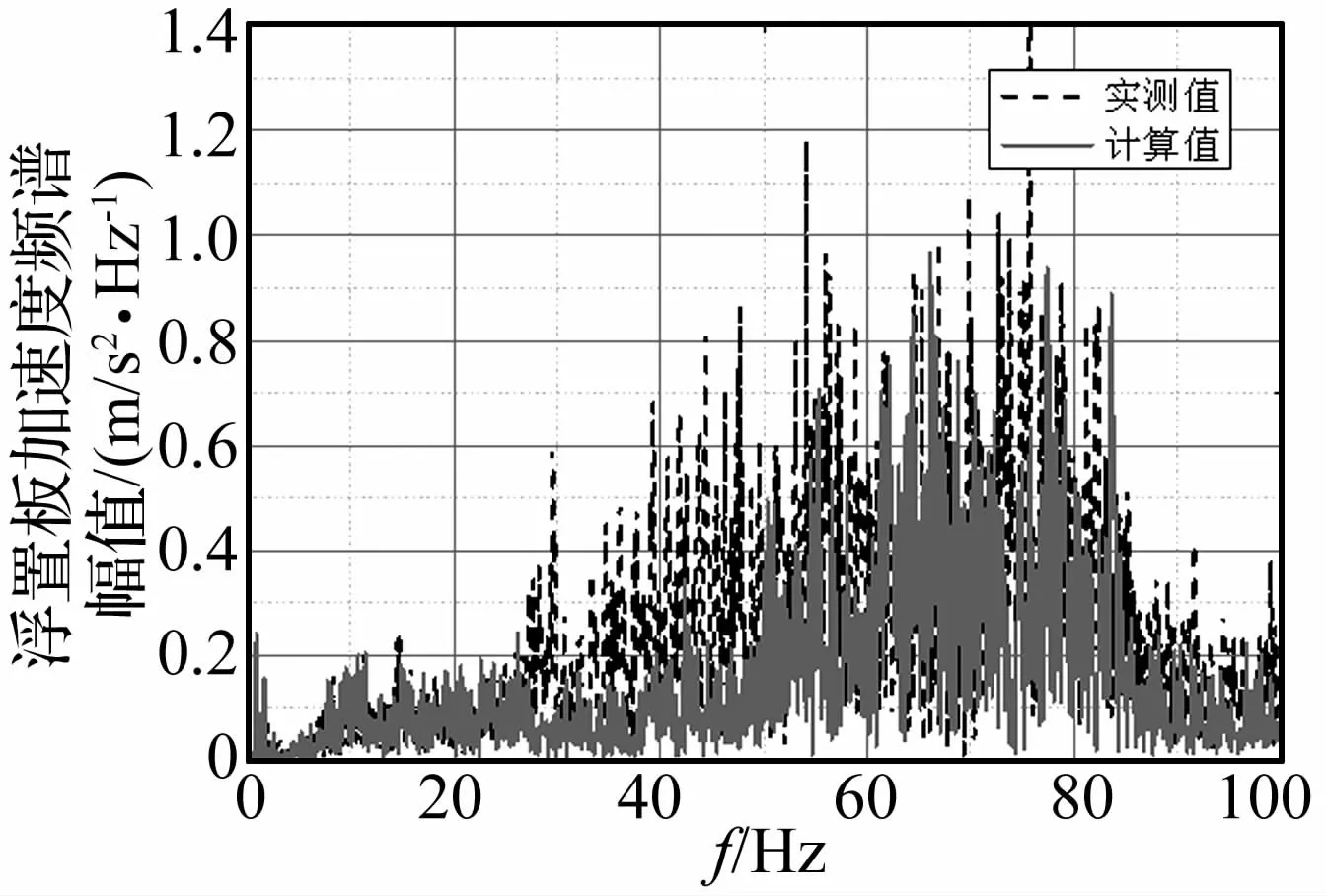
图8 浮置板振动加速度频谱幅值实测与计算值对比Fig．8 Comparison of acceleration frequency spectrum of FST

图9 浮置板振动加速度1／3倍频程实测与计算值对比Fig．9 Comparison of acceleration one-third octave spectrum of FST

3．3 地表振动加速度验证

采用本文提出的预测模型编制程序进行地表振动响应预测，土层参数采用北京地铁4号线北大东门区间实际地勘参数，如表2所示。

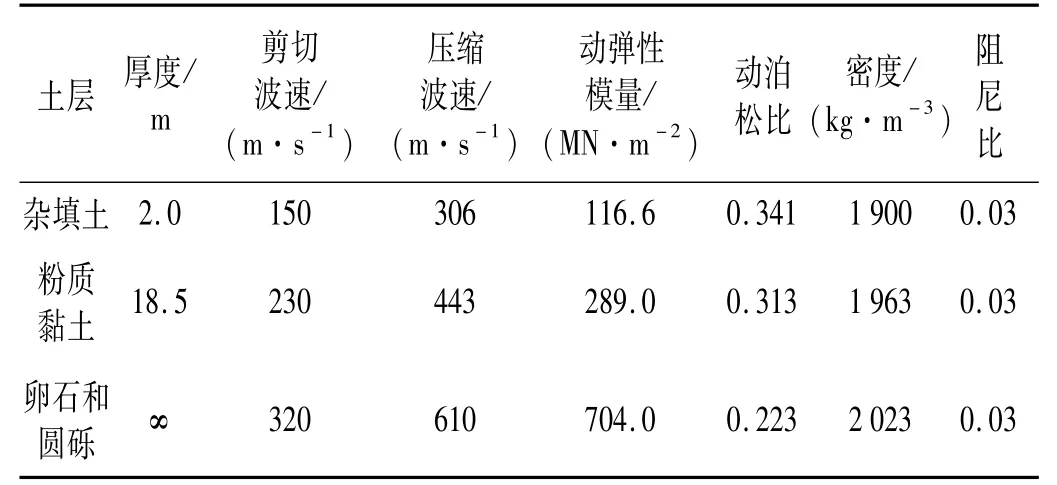
表2 土层参数Tab．2 soil parameters

图10为输入实际地勘土层参数的三维Green函数计算得到的频响函数群中，距离脉冲水平距离40 m和100 m处的典型频谱幅值。可以看出，土层地表频响函数随着频率的增加呈现“波浪形”变化趋势，而且100 m处的响应在全频带都比40 m处的响应量值有很大的降低。这说明随着距离脉冲位置水平距离的增加，土体对频域内振动的传播具有很强的衰减效果。

图11～图12为地表振动加速度频谱和1／3倍频程谱的实测值与计算值的对比。可以得出：

（1）模型预测和实测地表振动加速度的频谱波形相近，量级相当，振动主频都在8～10 Hz的钢弹簧浮置板的固有频率附近，而且两者的频域振动幅值相当。在35～50 Hz频段现场实测频谱有除了8 Hz自振频段峰值外的第二个小峰值群，计算值在此频段偏小。

（2）模型计算值和实测值的1／3倍频程谱曲线基本重合，振动量级、变化趋势一致。在40 Hz频带计算值稍低，这与频谱分析结果相符。

（3）Z振级计算结果为：地表实测Z振级54．0 dB，预测模型计算Z振级为56．1 dB，预测结果偏于安全且误差较小。

图10 地表振动加速度频响函数幅值Fig．10 Acceleration frequency response functions of ground points

图11 地表振动加速度频谱幅值实测与计算值对比Fig．11 Comparison of ground acceleration frequency spectrum

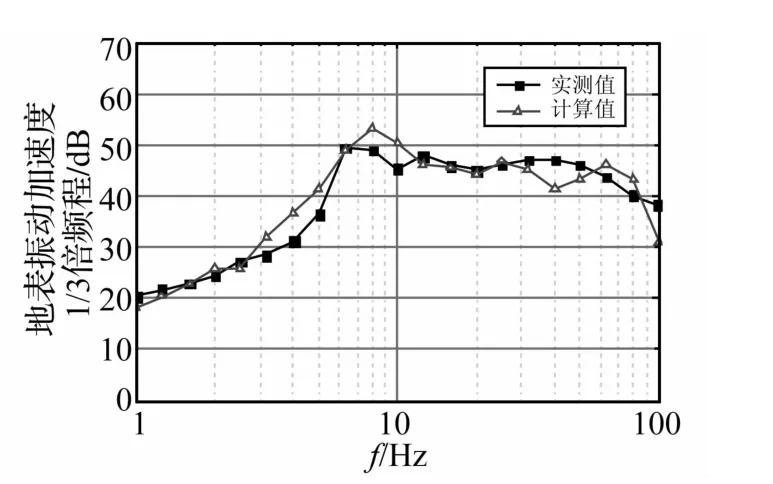
图12 地表振动加速度1／3倍频程实测与计算值对比Fig．12 Comparison of ground acceleration one－third octave spectrum

由于本预测方法旨在频域内解决地铁环境振动评价中的多点同时、快速准确预测问题，为了可以采用解析的方法求解土层频响函数从而提高计算速度，本预测模型采用Green函数法求解土层频响函数群。因为Green函数法是针对水平成层弹性体振动响应的纯解析模型，无法引入隧道结构进行解析求解，因此本模型在求解土层频响函数时进行了简化，忽略掉了隧道结构的影响。由本模型计算结果与实测的对比分析可以看出，在简化了隧道结构对振动的影响下，振动预测结果是较为精确的。说明本模型做出的这个简化是合理的，取得了地铁环境振动预测中计算速度和预测精度的平衡。

4 结 论

在土层振动传递固有特性的基础上，针对地铁建设设计阶段的多点快速预测要求，提出了一种浮置式轨道引起地表振动响应的频域解析预测模型，利用求解浮置式轨道作用于基底的频域力群和土层振动频响函数群的方法来预测地铁浮置式轨道引起的地表振动响应。

本模型通过优化的解析解编程实现，采用符合实际动力特性的浮置式轨道模型与考虑实际土层中振动传播特性的三维Green函数求解频响函数，保证了模型预测的精度，且相比其他动力仿真模型具有极快的计算速度，可在设计阶段同时针对有高等级特殊减振需求的多个敏感点地铁区间开展浮置式轨道选型工作。

采用本模型预测了北京地铁4号线浮置板区间地表振动响应，并与现场实测进行对比验证，表明本模型具有预测速度快、预测精度高、预测频带宽等特点，可有效预测浮置式轨道区间的地铁列车运行引起的地表振动响应，从而合理选择减振轨道型式。本模型具有重大的工程应用和社会价值，是现有环评预测方法的有效补充。

［1］夏禾，曹艳梅．轨道交通引起的环境振动问题［J］．铁道科学与工程学报，2004，1（1）：44－51．XIA He，CAO Yan-mei．Problem of railway traffic induced vibration of environments［J］．Journal of Railway Science and Engineering，2004，1（1）：44－51．

［2］张宝才，徐祯祥．螺旋钢弹簧浮置板隔振技术在城市轨道交通减振降噪上的应用［J］．中国铁道科学，2002，23（3）：68－71．ZHANG Bao-cai，XU Zhen-xiang．Applications of the steel spring floating track bed for vibration and noise control in urban rail traffic［J］．Journal of China Railway Science，2002，23（3）：68－71．

［3］刘洪瑞，邹锦华，王荣辉．轨道交通橡胶浮置板式轨道结构动力设计参数研究［J］．铁道科学与工程学报，2009，6（2）：5－11．LIU Hong-rui，ZOU Jin-hua，WANG Rong-hui．Dynamic design parameters of rubber floating slab track structure for urban mass transit［J］．Journal of Railway Science and Engineering，2009，6（2）：5－11．

［4］金浩，刘维宁．蚁群算法耦合LS-DYNA梯式轨枕轨道动力特性优化［J］．振动与冲击，2013，32（2）：24－28．JIN Hao，LIU Wei-ning．Optimization of laddertype track using ant colony algorithm coupled with LS-DYNA［J］．Journal of Vibration and Shock，2013，32（2）：24－28．

［5］中华人民共和国环境保护部．HJ453－2008．环境影响评价技术导则——城市轨道交通［S］．北京：中国环境科学出版社，2008．

［6］刘维宁，马蒙，王文斌．地铁列车振动环境响应预测方法［J］．中国铁道科学，2013，34（4）：110－117．LIU Wei-ning， MA Meng， WANG Wen-bin． Prediction method for subway train-induced environmental vibration responses［J］．Journal of China Railway Science，2013，34（4）：110－117．

［7］马龙祥，刘维宁，李克飞．移动荷载作用下浮置板轨道振动响应的频域快速数值算法［J］．铁道学报，2014，36（2）：86－94．MA Long-xiang，LIU Wei-ning，LI Ke-fei．Fast numerical algorithm of floating slab track vibration response under moving loads in the frequency domain［J］．Journal of the China Railway Society，2014，36（2）：86－94．

［8］Schevenels M． The impact of uncertain dynamic soil characteristics on the prediction of ground vibrations［D］．Leuven：K．U．Leuven，2007．

［9］Degrande G，Clouteau D，Othman R，et al．A numerical model for ground-borne vibrations from underground railway traffic based on a periodic finite element-boundary element formulation［J］．Journal of Sound and Vibration，2006，293（3－5）：645－666．

［10］刘卫丰．地铁列车运行引起的隧道及自由场动力响应数值预测模型研究［D］．北京：北京交通大学，2009．

［11］王文斌．基于脉冲实验的地铁环境振动响应传递函数预测方法研究［D］．北京：北京交通大学，2011．

［12］马龙祥，刘维宁，李克飞．浮置板轨道上轮对相互影响系数的求解［J］．中南大学学报（自然科学版），2013，44（12）：5068－5074．MA Long-xiang， LIU Wei-ning， LI Ke-fei． Calculation method of wheelsetsinteraction coefficient on floating slab track［J］．Journal of Central South University（Science and Technology），2013，44（12）：5068－5074．

［13］Kausel E． Fundamental solutions in elastodynamics： a compendium［M］．New York：Cambridge University Press，2006：140－184．