多层介质阻抗匹配对隔爆效果的影响
2014-09-20王晓鸣李文彬贾方秀殷婷婷
陈 闯,王晓鸣,李文彬,贾方秀,殷婷婷
(南京理工大学 智能弹药技术国防重点学科实验室,南京 210094)
战斗部在冲击波作用下的响应研究对弹药安全技术发展有重要意义,外界冲击波首先作用于战斗部的壳体,冲击波在壳体中的衰减和耗散直接决定战斗部中炸药的响应程度,因此高效隔爆结构的设计已成为弹药领域的热点研究问题。传统的单一材料对爆炸冲击波的衰减已进行了大量研究[1-4],获得了冲击波在不同材料中的衰减规律,但单一材料只能依靠增加介质厚度来提高隔爆结构的抗冲击能力,这将导致战斗部的重量及成本的增加。
近年来,多层组合介质用于隔爆吸能方面已得到国内外很多学者的关注。Tedesco等[5]提出采用分层结构能够更有效的削弱爆炸冲击波,并从界面反射率和透射率出发,研究了分层材料对冲击波的衰减特性;Petel等[6]通过改变一定厚度的钢和泡沫材料的层分布,设计了三种多层方案,结果表明冲击波压力的衰减随着介质层数的增加而加快。石少卿等[7]设计了一种钢—泡沫铝—钢复合结构隔爆装置,并利用LS-DY-NA软件对其隔爆性能进行了计算,达到了较好的吸能减振效果;王宇新等[8]对应力波在复合介质中的衰减进行了一维理论分析,得到了多层材料能提高结构的抗冲击能力及有效衰减冲击波透射强度;唐廷等[9]运用应力波理论研究了夹芯板中爆炸冲击波的传播规律,获得了夹芯板的运动规律和破坏特征。但是多层介质的组合方式对隔爆效果有着重要的影响,如何组合几种不同材料实现最佳衰减冲击波的性能,在设计隔爆结构时需重点考虑材料的阻抗匹配,在多层介质阻抗匹配特性对隔爆效果的影响等方面还很少见诸报道。
本文将45#钢、铝和有机玻璃三种材料组合成顺序波阻抗梯度、逆序波阻抗梯度以及硬软硬三种多层隔爆结构,对不同组合方式的多层介质进行了隔爆实验和数值模拟。研究了各层介质冲击波峰值压力、第三层介质能量与冲量的变化规律,分析了阻抗匹配特性对分界面透射系数的影响。
1 多层介质阻抗匹配对透射冲击波强度的影响分析
相比于单层材料的隔爆结构,多层介质衰减爆炸冲击波的能力有着显著的提高。阻抗是计算介质在动载荷作用下响应规律的重要条件[10],组合介质的阻抗匹配特性是影响冲击波衰减的关键因素,不同的阻抗匹配会导致界面处的冲击波的反射与透射存在差异。因此,多层介质存在最佳的排序方式削弱爆炸冲击波。
本文选择45#钢、铝和有机玻璃三种材料进行组合,材料的阻抗[11]如表1所示。根据材料的阻抗大小,设计了阻抗由小到大的顺序阻抗、阻抗由大到小的逆序阻抗和两端阻抗大中间阻抗小的硬软硬三种方案,每种方案的组合方式如表2所示。表中第一层为距离炸药最近的介质,第三层与炸药的距离最远。

表1 三种材料阻抗Tab.1 The impedance of materials

表2 组合方案Tab.2 The combination scheme
由冲击波理论[12]可知,冲击波在两种介质分界面处反射波的类型取决于介质的阻抗。当冲击波从介质Ⅰ传播至介质Ⅱ时,如果介质Ⅰ的阻抗大于介质Ⅱ,界面处将会反射稀疏波,反之反射波为冲击波。当药柱与可压缩介质接触爆炸,在炸药与介质的分界面处产生的入射冲击波压力取决于介质的阻抗。方案A第一层介质有机玻璃的阻抗小于炸药阻抗,反射波类型为稀疏波,而方案B和方案C的反射波类型为冲击波。根据炸药的状态方程、冲击波Hugoniot方程、爆轰波CJ面上产物参数和爆轰产物等熵方程可以计算出不同反射波类型的分界面处入射冲击波压力和质点速度的关系。
当反射波为稀疏波时:

当反射波为冲击波时:
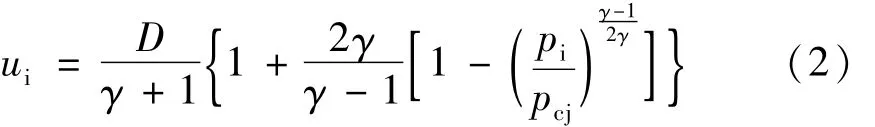
式中:ui为波后质点速度;pi为分界面处入射冲击波压力;D为炸药爆速;γ为炸药多方指数;pcj为炸药CJ爆轰压力。
利用介质中透射冲击波前后质量守恒方程、动量守恒方程和固体中冲击压缩规律可以求得:
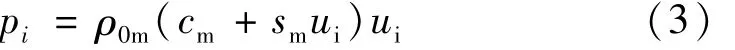
式中:ρ0m为介质的初始密度;cm为介质的声速;sm为与材料性质相关的常数。
联立方程(1)~(3),各材料参数参见文献[12],计算出方案A的入射冲击波压力为24.2 GPa,方案B和C的入射冲击波压力为39.8 GPa。
冲击波在介质中传播时,压力峰值随传播距离呈指数衰减,衰减方程表示为:

式中:px为冲击波传播至距离x时的压力;α为衰减系数。根据文献[3]中的实验数据,拟合得到的冲击波在45#钢、铝和有机玻璃中的衰减系数分别为0.076、0.058、0.045。
当冲击波传播至两层介质分界面处,反射波与透射波的计算采用介质Hugoniot关系曲线计算,如图1所示。曲线1~3分别表示不同介质的Hugoniot关系曲线,介质的阻抗越大,由原点出发的与雨果尼奥曲线上点的连线斜率越大。因此1~3表示的介质分别为铝、45#钢和有机玻璃。
当冲击波从介质1传入介质2时,压力为ph,分界面处的状态既应在反射波雨果尼奥曲线1’上,又应在介质2的右传透射波雨果尼奥曲线2上,即f点的状态,其中曲线1和1’呈镜像对称关系。同理,冲击波从介质1传入介质3时,状态从h点变为k点。曲线1’可以表示为:
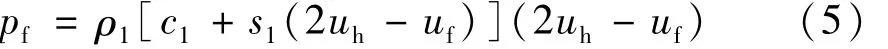
式中:pf和uf分别为f点冲击波压力和质点速度;uh为h点的质点速度;ρ1,c1和s1分别为介质1的初始密度、声速、与介质1性质相关的参数。

图1 反射波与透射波Hugoniot曲线Fig.1 Hugoniot curves of reflection and transmission wave
通过入射压力、衰减、反射和透射等冲击波传播过程的计算,求出最终从第三层介质输出的压力po。从而求出冲击波透射系数T为:

根据以上分析过程计算出三种方案的冲击波透射系数分别为 0.31、0.05、0.08。透射系数越小,说明衰减冲击波能力越强。以下分别从冲击波峰值压力、能量和冲量等不同方面分析,通过实验和数值模拟来研究阻抗匹配对多层介质隔爆效果的影响。
2 实验研究
2.1 实验装置和测试系统
多层介质隔爆装置的实验测试系统示意图如图2所示,实验测试系统由爆炸装置、锰铜压阻传感器、高速同步脉冲恒流源、示波器、触发探针及同轴电缆组成。药柱采用密度为1.6 g/cm3的黑索金(RDX),装药直径为60 mm,装药高度为45 mm,采用8#电雷管在药柱顶部中心起爆。为了减小爆炸后侧向稀疏波对测试结果的影响,与药柱接触的隔板直径为200 mm,厚度为10 mm。约束板的直径为200 mm,厚度为8 mm,中间隔板的直径为60 mm,每种介质的厚度为20 mm。
测试系统的工作过程为:炸药爆轰后,触发探针被导通,向恒流源发出信号使其开始给锰铜压阻传感器供电,同时示波器开始采集数据。当冲击波传至锰铜压阻传感器处,其电阻将发生变化,在示波器中显示为电压变化。冲击波压力可以根据传感器标定公式计算出来。
实验中采用H型锰铜压阻传感器,电阻为0.1Ω,传感器与示波器、恒流源之间通过50Ω同轴电缆连接,如图3所示。利用0.2 mm聚四氟乙烯薄膜包覆锰铜压阻传感器,将包覆的锰铜压阻传感器的敏感中心对准隔板中心。将传感器放置在多层介质之间,为保证锰铜压阻传感器与隔板之间紧密贴合,利用三个联接螺栓将整个装置夹紧。传感器的标定公式为:
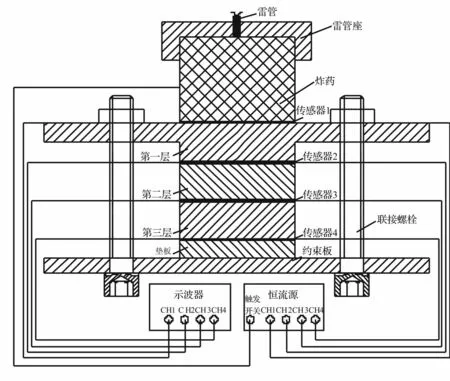
图2 实验测试系统示意图Fig.2 Sketch of experimental measurement system
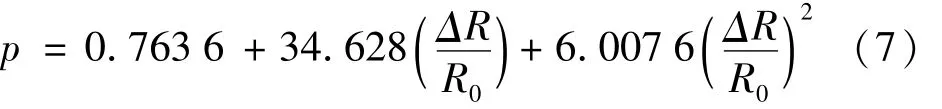
式中:p为冲击波压力(GPa),测试范围为1~45 GPa;R0为传感器的初始电阻,△R为电阻的改变量,△R/R0=△U/U0,U0为初始电压,△U为冲击波传至传感器处由于压阻效应产生的电压增量。

图3 锰铜压阻传感器Fig.3 Manganin pressure-resistance sensor
2.2 实验结果
实验采用的示波器采样频率为500 MHz,示波器记录的一组典型电压信号如图4所示,两个波形反映了测试的两个不同位置电压随时间的变化。冲击波到达传感器1早于传感器2,根据压力的第一次突跃可以计算出初始电压U,第二次突跃用来计算受冲击波作用后电压的增量△U,根据式(7)计算得到两个位置的冲击波压力,波形还可以得到冲击波压力的持续时间。从图中可以看出随着冲击波在介质中的衰减,冲击波压力峰值变小,压力持续时间变长。
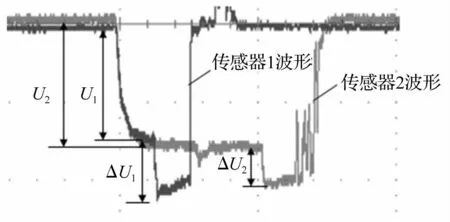
图4 示波器记录的波形Fig.4 The waveform gathered by the oscilloscope
为了比较各方案冲击波通过多层介质的传播特性,将锰铜压阻传感器分别放置在炸药与第一层介质之间、不同层介质分界面处,这样每个方案就需要测试四个位置的冲击波压力,如图2所示。为了准确测得多层介质的输出冲击波压力,在第三层介质的下面放置一块与其相同材质的垫板。各方案测试结果见表3,表中U、△U和p分别代表不同位置处的初始电压、电压增量及冲击波压力,1~4代表传感器的编号。传感器1~4按照距炸药由近到远的方式布置。传感器4测得的压力即为多层介质输出冲击波压力。从测试结果可以看出方案B的输出冲击波压力最小,方案A最大,说明逆序波阻抗梯度方案的衰减冲击波能力最强,这与以上阻抗匹配对透射系数的影响规律的分析结果是一致的。

表3 实验测试结果Tab.3 The experimental test results
3 数值仿真
3.1 计算模型
为了更直观地反映冲击波在多层介质中的传播过程以及获得更多的数据比较不同组合方式的隔爆效果,采用Autodyn有限元软件对多层介质衰减冲击波过程进行仿真计算,仿真模型如图5所示。炸药的状态方程选用 JWL(Jones-Wilkins-Lee)形式;由于 45#钢、铝和有机玻璃这三种固体介质在受到冲击波作用时产生的高压远超过材料强度极限,这样可以忽略固体材料的强度,将固体作为可压缩流体处理,选取Shock状态方程描述动态高压下冲击压缩过程,各材料模型参数取自文献[13]。炸药、45#钢、铝和有机玻璃均选择Lagrange算法,不同 Part之间的接触采用 Lagrange-Lagrange自由接触算法,为了获得在炸药-介质接触界面和不同介质分界面处的压力变化,炸药与第一层介质的分界面处高斯点设置为Gauge1,第一层介质与第二层介质的分界面处高斯点设置为Gauge2,第二层介质与第三层介质的分界面处高斯点设置为Gauge3,第三层介质与垫板的分界面处高斯点设置为Gauge4,在图5中分别表示为1~4。通过仿真获得多层介质的不同组合引起的冲击波在传播过程中各层介质压力、能量与冲量的变化规律。
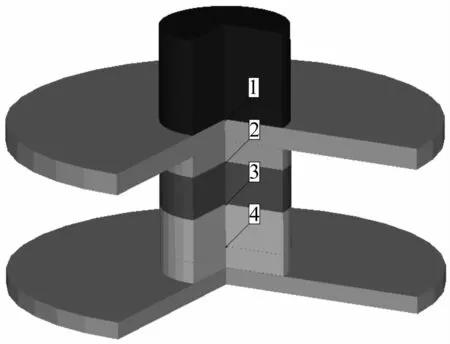
图5 仿真模型Fig.5 The simulation model
由于多层介质组合方式对冲击波衰减的影响主要取决于反射波类型,以方案C为例,不同时刻的硬软硬结构压力云图如图6所示。(a)为球面爆轰波在炸药中的传播,爆轰波阵面达到CJ压力;(b)此时冲击波传入第一层介质,压力随着传播距离的增大而逐渐衰减;(c)冲击波到达钢—有机玻璃分界面,从图中可以看出在钢中反射稀疏波,压力遭到削弱;(d)冲击波在第二层介质中传播;(e)冲击波传播至有机玻璃—铝分界面,在有机玻璃中产生一冲击波,压力有显著提高;(f)冲击波传至第三层介质,压力即为最终的输出压力。从压力云图可以清楚地观察到各阶段冲击波的衰减、反射和透射。
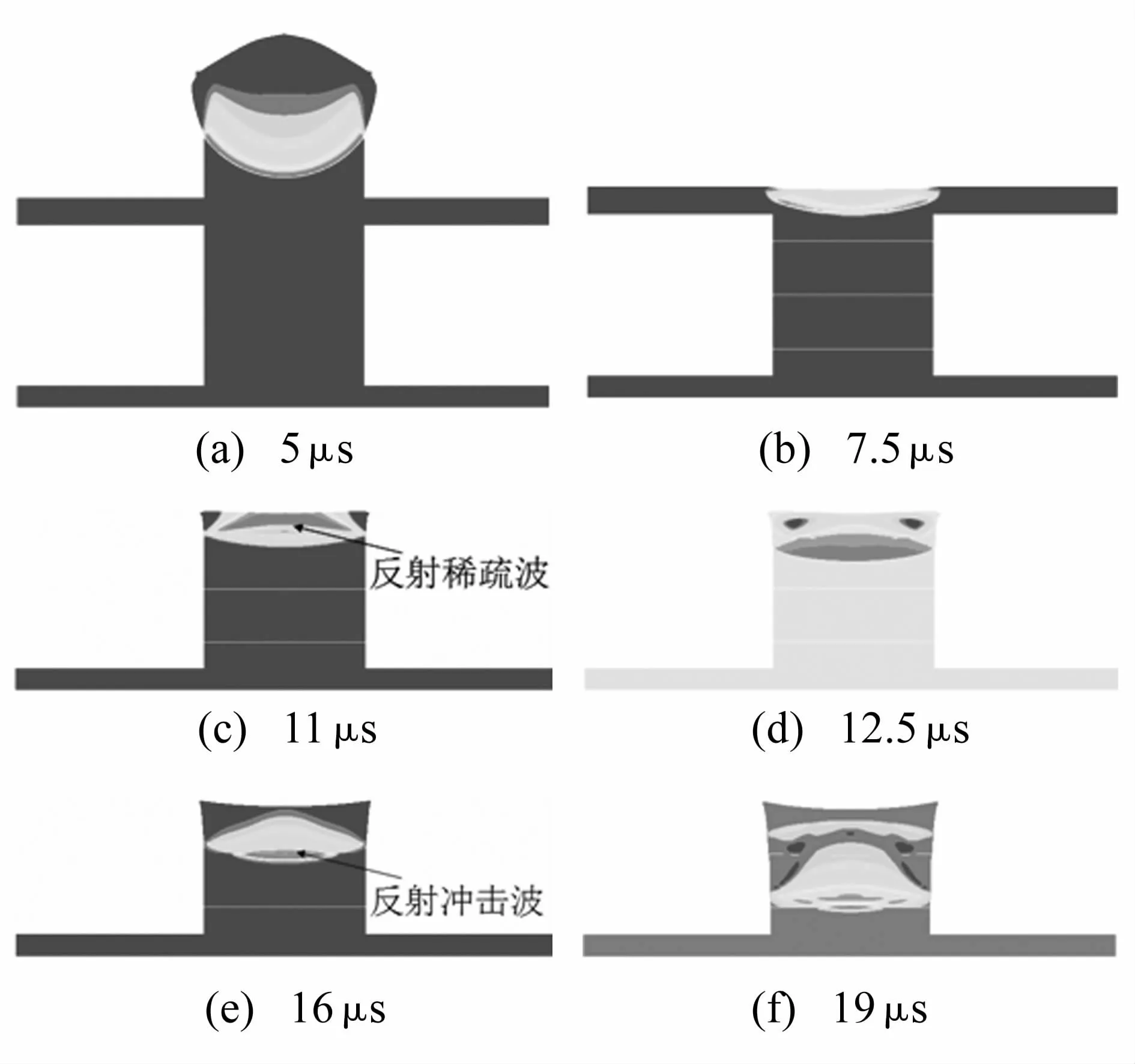
图6 硬软硬结构压力分布Fig.6 The pressure distribution of hard-soft-hard structure
3.2 冲击波压力衰减的理论、数值模拟与实验结果对比
为了定量研究不同介质组合造成的冲击波在介质分界面处的反射和透射,对分界面处的冲击波压力时程曲线进行分析。图7分别给出了方案A~C的不同Gauge点的冲击波压力随时间的变化曲线,从图中可以看出炸药与第一层介质接触处的压力最陡,下降迅速,随着在多层介质中的不断传入,压力下降平缓,作用时间变长,这与图4的实验结果是相符的。由高斯点的峰值压力可以看出冲击波在分界面处的反射情况,即不同的阻抗匹配所引起的不同反射波类型。
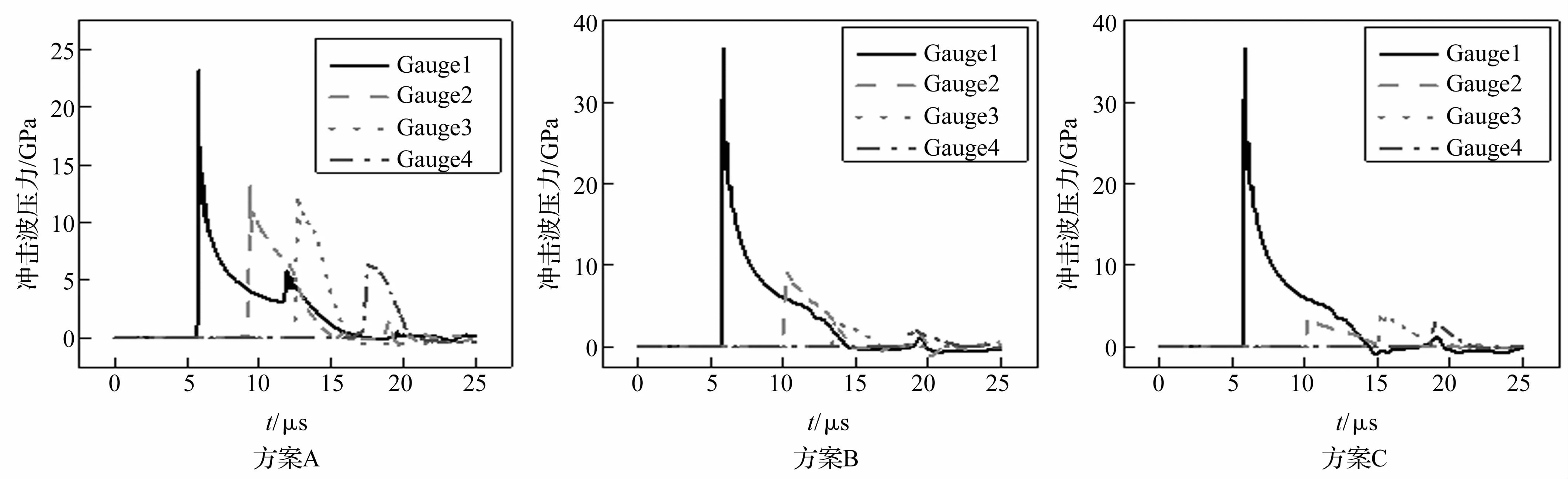
图7 不同组合冲击波压力随时间变化曲线Fig.7 The curves of shock pressure time-history for different combinations
不同方案冲击波峰值压力随传播距离的变化曲线如图8所示,图中分别给出了理论计算、数值模拟与实验的结果。从图中可以看出冲击波在各层介质中的衰减情况。从理论、仿真与实验测得的冲击波峰值压力的比较情况来看,方案B和C在炸药与第一层介质接触处的初始压力大于方案A,这是由于钢的阻抗大于炸药阻抗,而有机玻璃阻抗小于炸药阻抗。方案B和C在第一层介质中衰减速度快于方案A,当冲击波到达一、二层分界面处,方案B和C的压力已经小于方案A。理论、仿真与实验结果有一定的偏差,这是由于实验中传感器敏感中心的摆放位置会有一定的偏移,以及两层介质间的空隙等影响造成测试的误差。理论、实验与仿真得到的输出冲击波峰值压力由小到大分别为逆序波阻抗梯度、硬软硬结构、顺序波阻抗梯度。逆序波阻抗梯度的衰减冲击波性能最好,较顺序波阻抗梯度结构的输出压力降低了约67%。
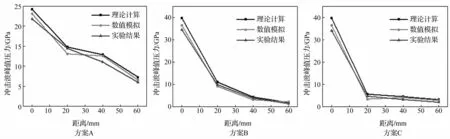
图8 冲击波峰值压力随传播距离变化曲线Fig.8 The curves of shock peak pressure changing with propagation distance
3.3 不同组合介质能量与冲量的变化
冲击波压力的不同直接影响系统内能量与动量的分配,为了研究能量与动量的演化特性,利用仿真比较三种方案的能量与冲量。在隔爆结构设计中,第一层与第二层介质吸能越多对隔爆效果越有利,而输入到第三层的能量越少越好。不同方案第三层介质的能量随时间变化曲线如图9所示。
从图中可以看出,方案A~C的第三层介质最终吸收的能量分别为4 800 J、1 077 J、2 010 J。说明逆序波阻抗梯度结构的方案吸能效果最好,而顺序波阻抗梯度结构的吸能效果最差。方案B的吸收的能量较方案A减少了78%。
从各层介质的冲量角度考虑,第三层介质冲量越大,多层介质的稳定性越差,越不利于整体结构的隔爆性能。图10为三种方案第三层介质的冲量时程曲线,从图中可以看出方案A~C的第三层介质最终的冲量分别为 12 Pa·s、2.4 Pa·s、5.7 Pa·s。方案 B的冲量值最小,说明逆序波阻抗梯度结构的稳定性最好。
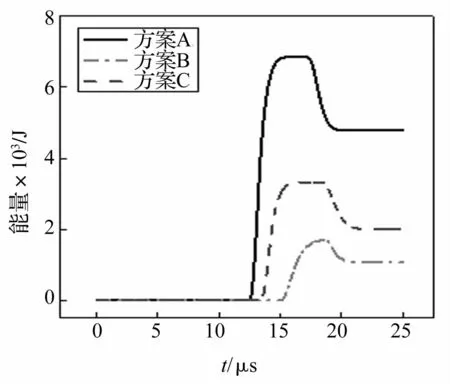
图9 不同组合第三层介质能量随时间变化曲线Fig.9 The curves of the third layer media energy time-history for different combinations
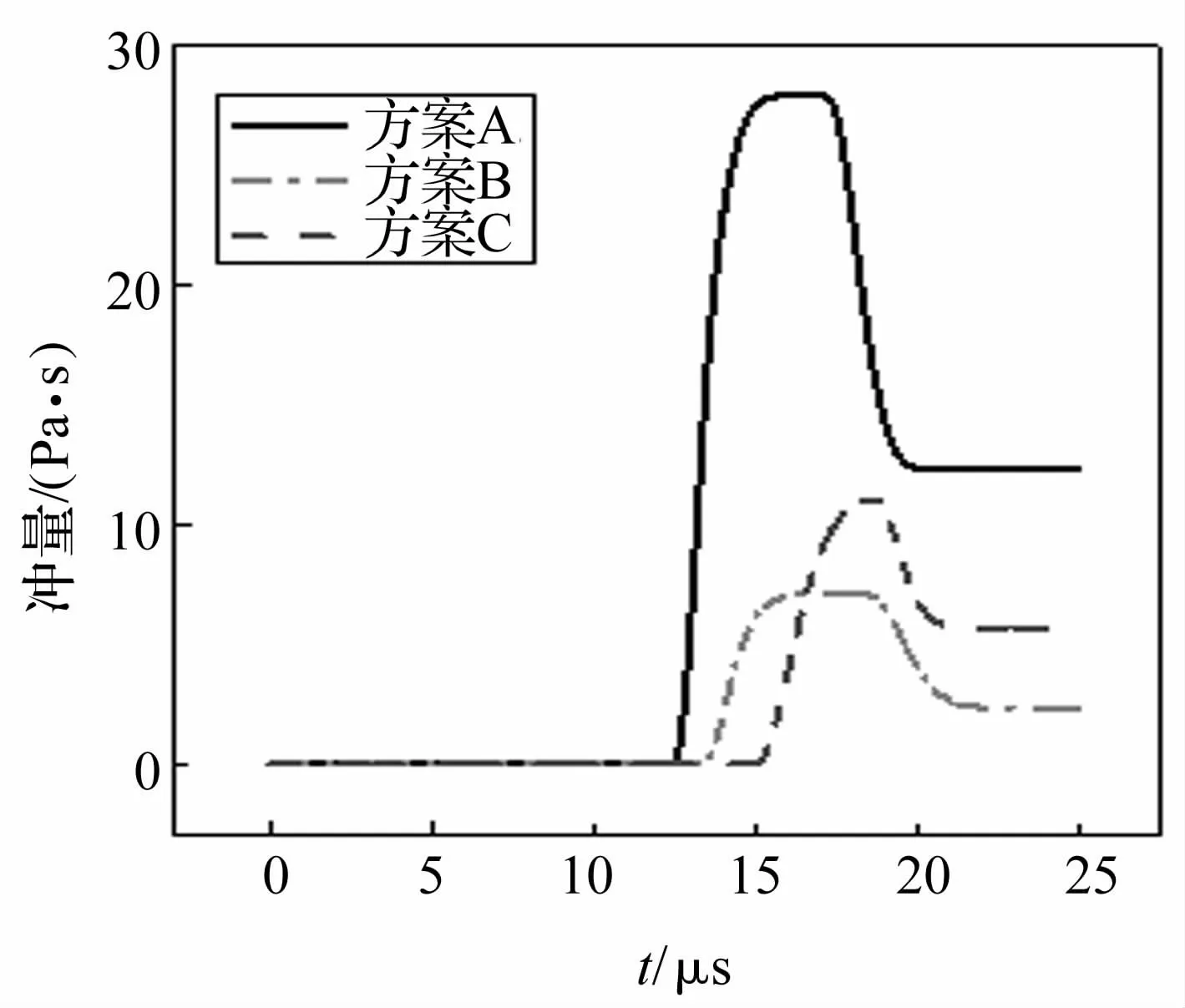
图10 不同组合第三层介质冲量随时间变化曲线Fig.10 The curves of the third layer media impulse time-history for different combinations
4 结 论
本文选取了45#钢、铝和有机玻璃三种材料进行不同方式的组合,设计出顺序波阻抗梯度、逆序波阻抗梯度以及硬软硬三种隔爆结构,通过理论、实验和数值模拟研究了阻抗匹配对多层介质隔爆效果的影响,得到了以下结论:
(1)利用爆炸冲击波理论对初始冲击波入射压力、衰减、反射和透射等传播过程进行了计算,通过锰铜压阻传感器测得了炸药与第一层介质接触面、不同介质分界面的冲击波压力历史。理论、仿真及实验的结果表明逆序波阻抗梯度的衰减冲击波性能最好,较顺序波阻抗梯度结构的输出压力降低了约67%。
(2)数值模拟获得了第三层介质的能量与冲量变化规律,逆序波阻抗梯度第三层介质的能量与冲量较顺序波阻抗梯度结构分别减少了78%和80%。从不同方面说明了逆序波阻抗梯度的隔爆效果最好,分析结果可为新型隔爆吸能结构的设计提供参考依据。
[1]Drummond W E.Explosive induced shock waves.Part I.Plane shock waves[J].Journal of Applied Physics,2004,28(12):1437-1441.
[2]Ram O,Sadot O.A simple constitutive model for predicting the pressure histories developed behind rigid porous media impinged by shock waves[J].Journal of Fluid Mechanics,2013,718:507-523.
[3]陈熙蓉,王可,刘德润,等.冲击波在不同材料隔板中的衰减特征[J].兵工学报,1991,11(2):75-80.CHEN Xi-rong,WANGKe,LIU Run-de,et al.Characteristics of attenuation of shock waves in barriers of different materials[J].Acta Armamentar,1991,11(2):75-80.
[4]徐森,刘大斌,彭金华,等.药柱冲击波在有机玻璃中的衰减特性研究[J].高压物理学报,2010,24(6):431-437.XU Sen,LIU Da-bin,PENG Jin-hua,et al.Study on the shock wave attenuation of the booster charge in the PMMA gap[J].Chinese Journal of Pressure Physics,2010,24(6):431-437.
[5]Tedesco J W,Landis D W.Wave propagation through layered systems[J].Computers&Structures,1989,32(3):625-638.
[6]Petel O E,JettéF X,Goroshin S,et al.Blast wave attenuation through a composite of varying layer distribution[J].Shock Waves,2011,21(3):215-224.
[7]石少卿,刘仁辉,汪敏.钢板-泡沫铝-钢板新型复合结构降低爆炸冲击波性能研究[J].振动与冲击,2008,27(4):143-146.SHI Shao-qing,LIU Ren-hui,WANG Min.Shock wave reduction behavior of a new compound structure composed of a foam aluminum layer between two steel plates[J].Journal of Vibration and Shock,2008,27(4):143-146.
[8]王宇新,顾元宪,孙明.冲击载荷作用下多孔材料复合结构防爆理论计算[J].兵工学报,2006,27(2):375-379.WANG Yu-xin,GU Yuan-xian,SUN Ming.Blast resistant calculation of compound structure with porous material under impact load[J].Acta Armamentar,2006,27(2):375-379.
[9]唐廷,韦灼彬,朱锡,等.近距爆炸作用下叠层复合夹芯板局部层裂破坏的理论研究[J].振动与冲击,2013,32(24):15-21.TANG Ting,WEI Zhuo-bin,ZHU Xi,et al.Theoretical study on local spalling fracture of a laminated composite sandwich plate subjected to close blast loading[J].Journal of Vibration and Shock,2013,32(24):15-21.
[10]吴文兵,蒋国盛,窦斌,等.嵌岩特性对嵌岩桩桩顶纵向振动阻抗的影响研究[J].振动与冲击,2014,33(7):51-57.WU Wen-bing, JIANG Guo-sheng, DOU Bin, et al.Influence of rock-socketed characteristics on vertical dynamic impedance at head of a rock-socketed pile[J].Journal of Vibration and Shock,2014,33(7):51-57.
[11]张庆明,刘彦,黄风雷.材料的动力学行为[M].北京:国防工业出版社,2006.
[12]张宝平,张庆明,黄风雷.爆轰物理学[M].北京:兵器工业出版社,2009.
[13]Century Dynamics Ltd. Interactive non-linear dynamic analysis software user manual[Z].Ramon USA:Century Dynamics Incorporated,2001:86-102.
