弹道导弹再入段跟踪制导算法研究*
2014-09-20侯煜博沈晓峰李思思
侯煜博,沈晓峰,李思思
(电子科技大学电子工程学院,成都 611731)
0 引言
弹道导弹(tactical ballistic missile,TBM)作为现代战争中威力极强的进攻性武器,具有射程远、精度高、速度快、杀伤力大、突防能力强等特点,给导弹防御提出了严峻的挑战。稳定的跟踪和精确的制导是导弹拦截成功的关键,是导弹防御雷达的核心任务。
由于导弹末段高速机动的特性,传统的匀速(CV)、匀加速(CA)模型在滤波过程中会产生较大误差。文中针对再入大气层的来袭导弹目标,通过分析其运动规律,从解析导弹运动方程入手,在东北天(East-North-Up,ENU)坐标系下建立目标状态方程,应用扩展卡尔曼(extended Kalman filter,EKF)滤波,对目标进行跟踪。
在给定来袭目标运动规律、拦截弹飞行速度规律和具体导引方法的条件下,可以确定出将两者视作质点时导弹飞向目标的理想运动学弹道。许多文献仅在二维情况下或三维情况下目标做匀速直线运动时给出推导[1-3],文中将针对导弹的标准弹道轨迹给出三维制导图。
1 弹道轨迹生成
1.1 目标受力模型
TBM再入大气层后,主要受到重力和空气阻力作用,阻力影响通常超过重力,因此可以采用简洁的平方反比重力加速度模型代替椭球地球重力加速度模型,重力产生的加速度为:

空气阻力引起的加速度为:

标准大气参数公式可以参照文献[5]。为给后续雅克比矩阵求解带来方便,文中利用指数函数来近似拟合。图1为在ρ(h)= ρ0e-κh条件下的拟合结果与标准结果的对比图,其中ρ0和κ均为已知常数。由图可以看出拟合效果较为准确,最大偏差为0.0269kg/m3。

图1 大气密度函数精确值与拟合值的对比
1.2 弹道生成
仿真生成弹道轨迹是进行跟踪与制导的基础,根据受力模型,利用龙哥库塔积分目标动力学微分方程组的方式可以得到再入段导弹的弹道轨迹。
设计一条再入角度为39°的标准弹道,图2为弹道轨迹仿真图,图3为弹道参数。

图2 导弹再入段的弹道轨迹
2 跟踪算法
扩展卡尔曼滤波是最通用的非线性滤波方法,在确定了目标的状态方程与量测方程及其对应的雅克比矩阵后,即可应用EKF算法进行滤波。EKF算法流程可以参考文献[6]。根据受力模型推导出目标的状态方程和量测方程及其对应的雅克比矩阵是EKF滤波算法的关键。

图3 弹道参数
2.1 目标状态方程
当TBM再入大气层后(距海平面约91km以内),由式(1)、式(2)可知其加速度表达式为:

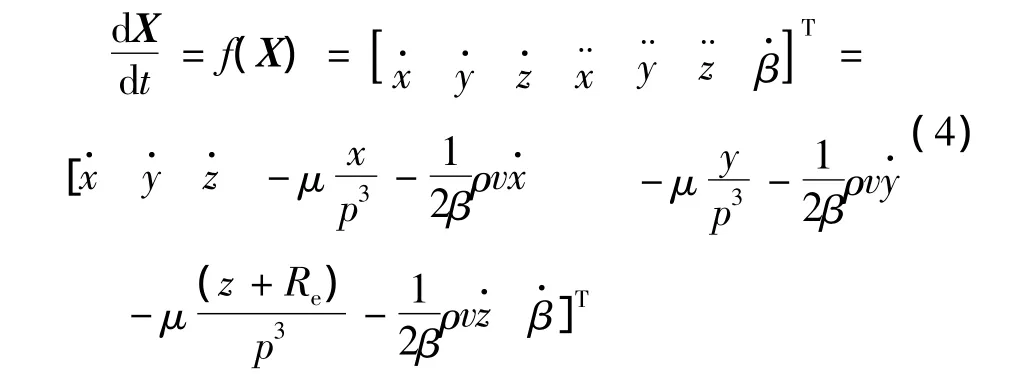

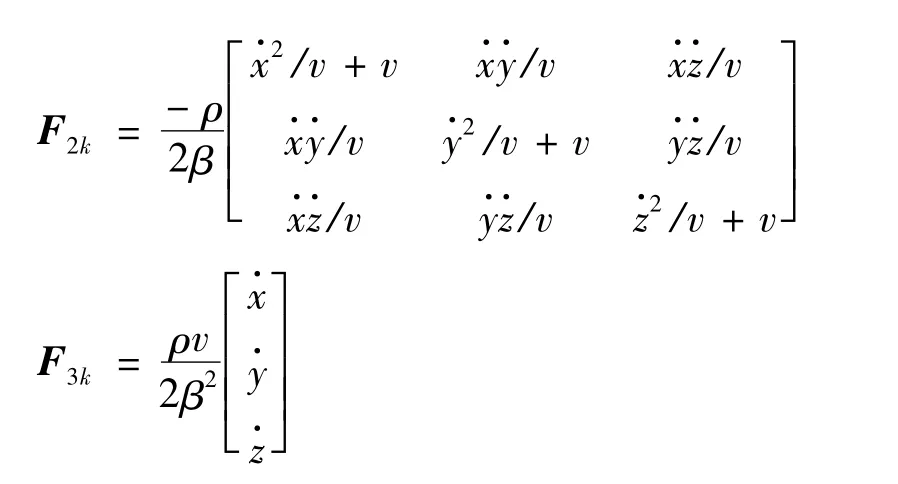
在采样间隔T下目标离散化的状态方程[7]为:

状态噪声w(k)为零均值白噪声序列,其方差为Q(k)。
2.2 目标量测方程
由于量测信息来自雷达站球坐标系,所以量测方程是非线性的,其表达式为:

量测噪声ω(k)的方差矩阵R(k)由雷达具体的距离、方位角、俯仰角测量误差确定。
量测方程的雅克比矩阵为:

在确定了上述状态方程与量测方程及其相应的雅可比矩阵后,即可应用EKF进行滤波。
3 比例导引制导
假定在上述滤波过程中已获得来袭目标的运动规律且拦截弹的速度变化规律已知,如何将导弹引向目标便是制导规律所要完成的任务。比例导引法是一种最常用的、制导精度较高的制导规律。追踪法、前置角法、平行接近法都可以看作是比例导引法的特殊情况。
比例导引法是指拦截弹飞行过程中速度矢量Vm的转动角速度dθm/dt与导弹、目标连线的旋转角速度dq/dt成比例的导引方法[9]。图4与图5分别为导弹与目标相对位置和比例导引示意图。

图4 导弹、目标相对位置
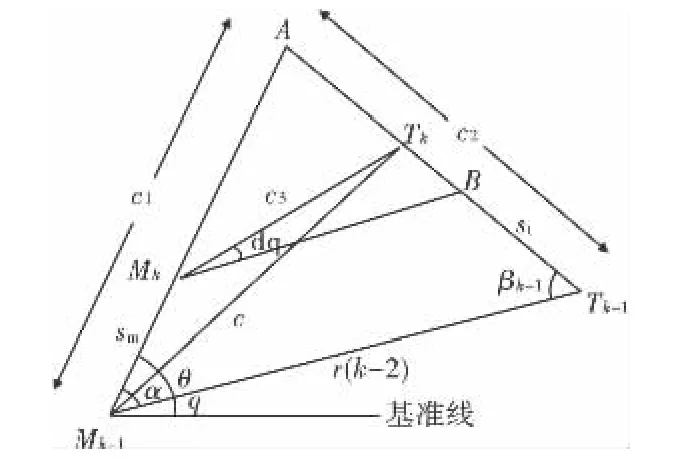
图5 比例导引示意图
图中 Mk-1、Mk、Tk-1、Tk分别为 k - 1时刻、k时刻导弹位置和k-1时刻、k时刻目标位置。A为Mk-1Mk与 Tk-1Tk交点,MkB 平行于 Mk-1Tk-1。
设 xt、yt、zt表示目标坐标,任意时刻的 xt、yt、zt已知。算法流程如下:
k-1时刻导弹与目标的距离:

k-1时刻目标速度矢量与导弹、目标连线的夹角:


k时刻导弹、目标连线与基准线夹角增量:为k-1时刻导弹与k时刻目标之间距离,st=vt(k-1)·Δt,即在Δt内将目标视为做匀速直线运动。
比例导引法的差分方程为:

利用余弦定理求得:


设xA、yA、zA表示A点坐标,xm、ym、zm表示导弹坐标,由几何关系知:

其中sm=vm(k-1)·Δt,即在Δt内将导弹视为做匀速直线运动。在获得k时刻的导弹坐标后即可更新r(k)进行下一次循环。必要时还要利用c3对dq进行校正。
4 仿真分析
4.1 跟踪滤波结果
假定雷达在跟踪再入段时的量测标准差为:σR=10m,σA= σE=1mrad。跟踪数据率设定为100Hz。采用两点法初始化状态变量,初始协方差可以参考文献[10]。在滤波过程中,状态噪声为设计参数,文中采用分段噪声,先利用较大噪声使算法快速收敛,再采用较小噪声降低滤波误差。对目标的跟踪精度采用均方根误差(RMSE)作为判别标准[11],设X^n( )k|k为k时刻第n次蒙特卡罗的状态估计值,则:
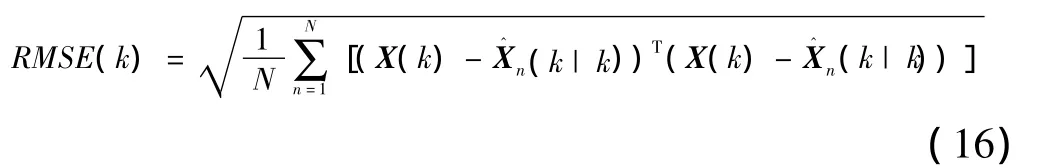
对量测数据进行一次滤波,得到真实轨迹、量测点迹与滤波轨迹的结果见图6。蒙特卡罗仿真500次得到均方根误差结果如图7。

图6 导弹再入段的真实、量测、滤波轨迹
为方便对比,图7中给出了针对上述相同轨迹应用CV模型的滤波结果。由图可以看出算法滤波收敛速度较快,误差较小且收敛后基本稳定。较CV模型滤波精度有较大提升。合理改变跟踪数据率或雷达量测误差,在不同的弹道模型下进行多次仿真比较,结果类似。

图7 再入段滤波的位置RMSE误差
4.2 制导结果
设定比例系数为K=5,导弹初始位置为坐标原点,速度恒定为 3000m/s,时间间隔 Δt=0.01s,导弹与目标之间相对距离小于60m时认为制导成功。获得三维理想拦截弹弹道仿真图见图8,图9为拦截弹的法向过载。

图8 理想三维弹道仿真

图9 拦截弹法向过载
5 结束语
文中针对再入大气层的来袭导弹目标受力情况推导了ENU坐标系下目标运动加速度表达式,建立了混合坐标系下的目标状态方程与量测方程,通过受力分析采用基于其特性的弹道模型进行滤波,给出了状态估计与协方差矩阵的初始值计算方法,采用EKF滤波算法对目标进行跟踪,为制导过程提供了来袭导弹的速度位置信息。利用比例导引制导律进行仿真得到三维制导图。仿真结果表明,算法可以有效的对再入类导弹进行稳定的跟踪和精确的制导。
[1]高尚.比例导引理想弹道仿真[J].计算机工程与设计,2003,24(8):66-68.
[2]陈宇强,赵育善.导弹最优制导律弹道仿真分析[J].指挥控制与仿真,2007,29(3):92-105.
[3]周纪元,童幼堂,张磊,等.典型导引规律三维弹道仿真分析[J].舰船电子工程,2008,28(2):110-112.
[4]张毅,肖龙旭,王顺宏.弹道导弹弹道学[M].长沙:国防科技大学出版社,2005.
[5]杨炳尉.标准大气参数的公式表示[J].宇航学报,1983(1):83-86.
[6]何子述,夏威.现代数字信号处理及其应用[M].北京:清华大学出版社,2009.
[7]易令,吕明.使用交互多模型算法的高速高机动目标跟踪[J].雷达科学与技术,2006,4(3):143-147.
[8]辛召强,沈晓峰.利用CUDA快速实现IMM目标跟踪[J].雷达科学与技术,2012,10(6):656-659.
[9]梁慜.弹道导弹拦截仿真建模技术研究[J].中国电子科学研究院学报,2013,8(1):56-59.
[10]何友,修建娟,张晶炜.雷达数据处理及应用[M].北京:电子工业出版社,2006.
[11]张丕旭,石章松,刘忠.一种基于弹道模型的机动目标跟踪算法[J].弹箭与制导学报,2009,29(4):55-57.
