一种用于复合轴系统的机动目标跟踪算法*
2014-09-20尹小杰
袁 佳,尹小杰,柯 芳,吴 斌,樊 键,程 川
(1西南技术物理研究所,成都 610041;2空军驻川西军事代表室,成都 610041)
0 引言
复合轴ATP系统,通过分别控制主轴工作范围大,但带宽较窄、精度较低的大口径望远镜与子轴工作范围较小,但频率宽、响应快、精度高快速反射镜(fast steering mirror,FSM)同时工作,以实现大范围的快速高精度跟踪。其原理如图1所示。

图1 双探测器型结构原理图
根据复合轴ATP系统的特点,可构建一个垂直于望远镜所在水平面的y、z二维平面,并可推算出目标航迹位于y、z平面上投影的状态观测量。这里,主系统观测量中只考虑粗探测器测得的脱靶量,而子系统观测量则是在前者的基础上引入了的精探测器测得的脱靶量后的重构结果。借助子系统的特点,第二套观测量将更加精确,从而提升跟踪精度。
而文中目标跟踪算法的任务,就是要通过对上述两组主、子系统观测量的数据处理,以实现对目标运动状态的实时估计与辨识。使得主系统的控制得到直接改善,进而使子系统的控制精度也随之提高,从而达到优化复合轴系统整体控制性能的目的;且当探测器观测信号被动中断时,使系统仍能根据目标航迹辨识结果保持一段时间的记忆跟踪,等待信号恢复,以减小目标丢失的概率。
1 跟踪算法发展现状
建立合适的运动模型和选用简单有效的滤波器,是解决机动目标跟踪问题的核心内容。目前,比较典型的运动描述模型如:匀速CV模型、匀加速CA模型、R.A.singer提出的 Singer模型[1]、周宏仁等提出的“当前”统计模型[2]、F.Berg提出的 Berg模型[3]、T.L.Song提出的 Song模型[4]及由 Mehrotra K 和Mahapatra P R提出的高度机动目标 (Jerk)模型[5]等;滤波算法方面,在经典算法维纳滤波、α-β-γ滤波、卡尔曼滤波等的基础上,又出现了一些新的自适应滤波算法,如文献[6]采用的变维滤波、文献[7]中强跟踪滤波器、文献[8]中粒子滤波、文献[9]中模糊自适应算法等。
为了应对机动目标的运动特征,于是出现了多模型混合系统。典型的如Blom和Bar-Shalom提出了一种交互式的多模型滤波器(IMM),目标状态由多个滤波器交互作用得到[10]。IMM算法是满足模型完备性与互斥性条件下的最优估计,有非线性滤波优势,目前是比较适用于高机动目标的跟踪算法。

图2 IMM算法示意图
2 机动目标跟踪算法的提出
2.1 算法思路
在IMM模型集构建时,若取得过于简单,则不能覆盖机动运动;若模型集中的运动模型种类过于复杂,将导致计算量加大及模型间多余竞争,使跟踪性能下降。于是文中提出如下思路:在主、子系统中采用各自的IMM运动模型集,对两组系统观测量进行独立滤波估计;然后把两组估计量通过分布式数据融合以实现主、子系统估计的优化组合,并将融合后的估计量作为主、子系统脱靶量计算及记忆跟踪航迹预测的依据。
2.2 算法方案的展开
首先设定:机动目标加速度范围为[-amax,amax],转弯速率范围为;主、子系统位于 y、z平面上目标状态观测量已经推算得出,且所涉及的系统噪声及观测噪声都为零均值高斯白噪声。
2.2.1 主、子系统独立滤波阶段
1)主系统IMM-CT方案:CT模型使用于目标在平面中做匀速圆周运动模式。现将均分成n1-1段,以端点及节点值为转弯速率构建n1个CT模型组成主系统IMM模型集。各模型通过独立卡尔曼滤波,再进行实时交互计算,得出主系统状态估计向量,同时提出用于数据融合的判别矩阵。设n时刻,主系统状态估计向量(元素依次表示目标y方向位置、速度、z方向位置、速度)为:

模型概率向量及n1个模型卡尔曼估计误差自相关矩阵分别为 μΙ(n)、PΙm(n)(m=1,2,…,n1,分别表示模型集中n1个模型),取:

则n时刻,主系统y、z方向的判别矩阵取为:

2)子系统IMM-CA方案:子系统中采用两块相互独立的快速反射镜,实现对激光光束在方位和俯仰方向上的控制,于是将目标的运动航迹分解到y轴和z轴上独立分析。这里选用适于描述匀加速直线运动的CA模型构建模型集,于是现将[-amax,amax]均分成n2-1段,以端点及节点值为加速度构建n2个CA模型组成子系统IMM模型集,同样选用卡尔曼滤波器对目标状态做出关于y、z方向的实时估计。
设n时刻,子系统状态估计向量(元素依次表示两个坐标轴方向的位置、速度、加速度)为:



则n时刻,子系统y、z方向的判别矩阵取为:

2.2.2 主、子系统数据融合阶段
文中采用分布式融合系统的思想,即各传感器独立滤波,而融合单元输出的最终估计量为主、子系统各自估计量的线性优化组合,若n时刻某传感器的估计精度差,则它对最终估计的贡献就比较小。取自估计误差自相关矩阵的判别矩阵 My、Mz、Ny、Nz也正是为了体现估计精度。文中在主系统模型集中引入了CT模型,以应对目标蛇形运动,但此模型对目标做加速运动时的状态估计效果不理想。于是,引入了自适应的调节系数,把状态最终估计误差控制在一定范围内。这里:
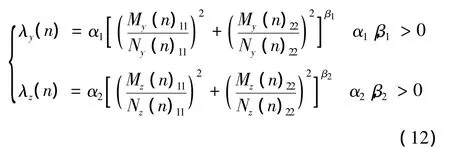
式中 α1、β1、α2、β2的取值应根据具体的观测噪声及系统噪声特性来选定,经过调试,使系统处于较优状态。则改进后的数据融合结果可为:
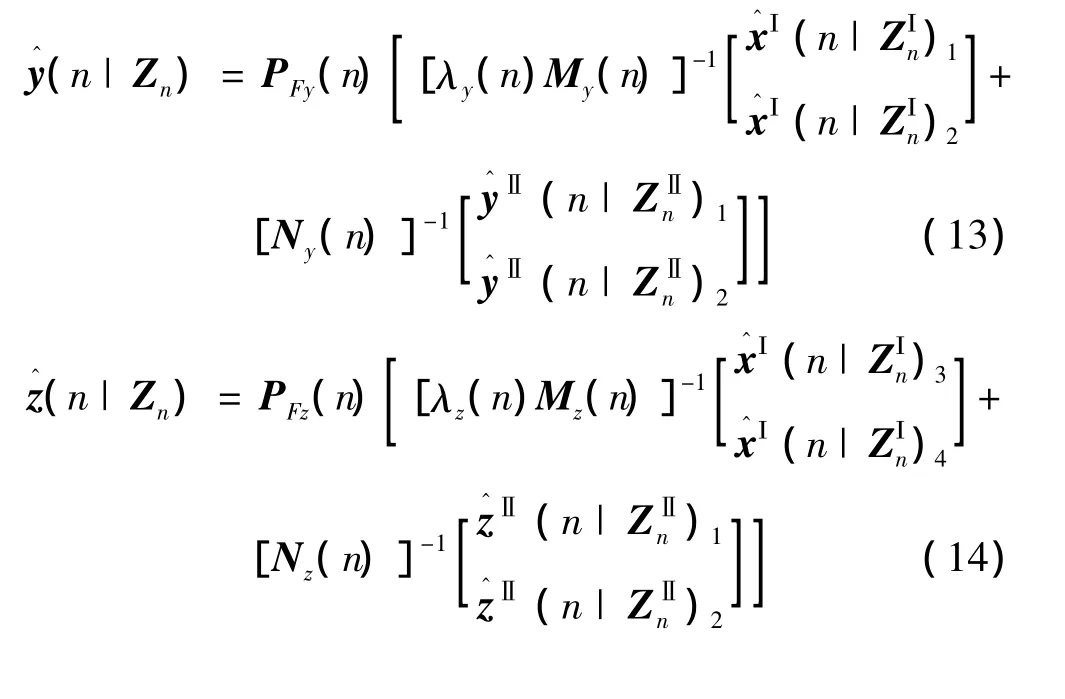
2.2.3 目标运动模式综合辨识阶段
此阶段、将根据状态最终估计量辨识出y、z轴上的加速度、转弯速率等运动特性。用于观测信号被动中断时,推测目标的运动模式以实现记忆跟踪。
3 MATLAB算法仿真
设定一个以望远镜所在位置为原点,初始位置为[4000m 6000m 4000m]的随机机动目标,其航迹在y、z平面投影如下:以[-172m/s 346m/s]的初速度,1~55s匀速直线运动,56~150s以1g(g=9.8m/s2)转弯速率匀速转弯,151~181s以ax=-5m/s2、ay=-18m/s2匀加速运动,182~ 255s以-2.7g转弯速率匀速转弯,256~284s匀速直线运动,285~324s以3g转弯速率匀速转弯,325~344s以ax=8m/s2、ay=4m/s2匀加速运动,345~379s以-1.8g转弯速率匀速转弯,380~400s匀速直线运动,如图3所示。主系统两方向观测噪声方差为25m2,CT模型匀速直线模式和匀速转弯模式时的系统噪声方差分别为3.5m2和6.5m2,子系统两方向观测噪声方差为16m2,CA模型匀速直线模式和匀加速直线模式时的系统噪声方差分别为3m2和9m2,主、子系统采样周期都为1s。

图3 机动目标航迹在y、z平面的投影
1)图4~图6为相同边界条件下,文中算法与经典“当前”模型算法分别做100次蒙特卡罗状态估计仿真结果的比较。

图4 经典“当前”模型下y轴方向位置跟踪
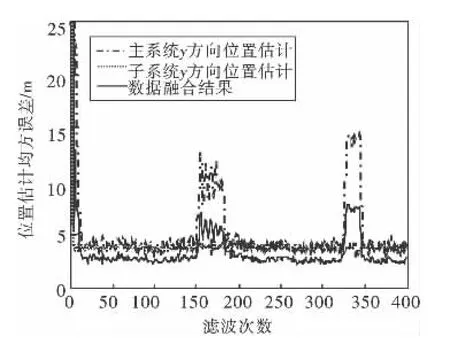
图5 文中算法y轴方向位置跟踪

图6 改进后的算法y轴方向位置跟踪
2)本算法1次试验对运动模式特性辨识举例(见图7)。

图7 文中的算法1次试验对运动模式特性辨识
比较图5和图6可见:通过基础分布式数据融合后的估计量,误差量较主、子系统都有所减小,但当特定情况下某分系统误差陡增时,其应对能力欠佳。引用改进的数据融合方法后,一定程度上抑制了上述不良情况,使最终估计结果更加准确。
通过MATLAB仿真可见:文中算法与采用“当前”统计模型的典型算法相比,其跟踪精度更优,且误差收敛速度相当;从用于记忆跟踪的角度分析,文中算法可以较准确地辨识出机动目标的位置、速度及转弯速率信息,为航迹预测提供依据。而“当前”模型只能估计出目标航迹切线方向上的速度及加速度,应对目标蛇形运动模式下的记忆跟踪比较困难;从计算量的角度分析,由于采用了数据融合,计算量将大于“当前”模型,但通过文中方案的处理使得各运动模型的转移矩阵得以固定,只需事先写入程序而不用在每次滤波时重新计算,从而在不影响精度的情况下将运算量控制在适中范围。
4 结论
文中提出的用于复合轴系统的目标跟踪算法方案,采用不同的IMM模型集的估计结果做数据融合,从而实现以相对少的运动模型种类覆盖更复杂的运动模式同时优化估计结果的目的。本算法易于计算机编程实现,且可根据系统要求调整n1、n2的取值,以调节跟踪精度。
值得注意的是:本方案引用的卡尔曼滤波器,是根据系统噪声方差和量测噪声方差实时修正滤波增益阵的,所以需要预先得到具体情况下系统噪声和观测噪声的统计特性,这是保证算法准确的前提之一;同时,对被跟踪目标的运动特性有一定程度的了解,也将有助于提高算法的精确度。
[1]R A Singer.Estimating optimal tracking filter performance for manned maneuvering targets[J].IEEE Transactions on Aerospace and Electronic Systems,1970,6(4):473-483.
[2]周宏仁,敬忠良,王培德.机动目标跟踪[M].北京:国防工业出版社,1991.
[3]F Berg.Estimation and prediction for maneuvering target trajectories[J].IEEE Transactions on Automation Control,1983,28(3):294-304.
[4]T L Song.Suboptimal filter design with pseudo measure for target tracking[J].IEEE Transactions on Aerospace and Electronic Systems,1988,24(1):28-39.
[5]Mehrotra K,Mahapatra P R.A jerk model for tracking highly maneuvering targets[J].IEEE Transactions on Aerospace and Electronics Systems,1997,33(4):1094-1105.
[6]钱琼芬,徐毓,金宏斌.变维交互作用多模型滤波方法[J].计算机测量与控制,2005,13(8):830-832.
[7]Yang Liu,Ma Zhao,Qinzhang Wu.A new hybrid grid multiple model estimation based on STF[J].Journal of Computers,2012,7(7):1607-1614.
[8]Yuan L,Zheng Y F,Zhu J,et al.Object tracking with particle filtering in fluorescence microscopy images:Application to the motion of neurofilaments in axons[J].IEEE Transactions on Medical Imaging,2011,31(1):117-130.
[9]唐磊,赵春霞,唐振民.基于模糊自适应Kalman滤波的GPS/DR数据融合[J].控制理论与应用,2007,24(6):891-894.
[10]Mazor E,Averbuch A,Bar-Shalom Y,et a1.Interacting multiple model methods in target tracking:A survey[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):103-123.
