一种基于分割法的无人机路径规划新方法*

单提晓，蒋 蓁

（上海大学机械工程与自动化学院，上海 200072）

0 引言

无人机的路径规划是无人机研究的一个重要领域，其目的是根据任务目标在有障碍环境中规划出一条满足约束条件的最优无碰撞飞行轨迹。文中提出的无人机路径规划方法基于Voronoi图法和Dijkstra算法。Voronoi图，又叫泰森多边形或Dirichlet图，是获取无人机安全飞行路径的一种常用方法，并且在计算机中容易实现，但是通过Voronoi图得到的路径往往比较曲折，并不是最优路径，很多情况下还存在多条可选路径。Dijksta算法解决的是有向图中单个源点到其他顶点的最短路径问题。结合Voronoi图法生成的可选路径，可以大大减少Dijkstra算法中需要计算的节点数量，从而提高算法执行效率。

1 问题描述

在无人机的路径规划过程中，存在的威胁主要有影响飞行安全的雷达、山峰、建筑等。在实际的路径规划中，为了减少计算量，需要对这些威胁进行简化。假设在10 km×10 km的飞行区域内分布有11个位置已知的敌方探测雷达，雷达的作用方式完全相同且相互独立，每部雷达的探测范围均为半径1 km。如图1所示为雷达分布图，其中圆圈表示每个探测雷达所能探测的最大范围，圆圈中点表示探测雷达所在位置。无人机在某一固定飞行高度相对于雷达做等速规避运动。无人机安全飞行区为图中所示圆圈以外的区域。

图1中左下方坐标为（0，2）的点为无人机飞行路径的起点，右上方坐标为（10，9）的点为飞行路径的终点。路径规划的目的就是在雷达探测范围以外的区域找到一条连接起点和终点并且满足约束条件、距离最短的路径。

图1 雷达分布图

2 路径规划方法

文中提出的路径规划方法基于Matlab软件平台，首先建立关于飞行区域内雷达点的Voronoi图以获取安全飞行路径。利用Dijkstra算法结合Voronoi图法获得的飞行路径计算出一条可连通并且长度最短的安全路径。若无法获得此路径，则算法结束。若可得到此路径，则使用文中提出的分割法对经Dijkstra算法得到的路径进行优化得到拐点数量更少的飞行路径。最后使用spcrv函数对所得路径进行最终优化得到平滑的最终安全飞行路径。如图2所示为文中路径规划算法工作流程图。

图2 路径规划算法工作流程图

2.1 建立关于雷达点的Voronoi图

在Matlab中利用Voronoi函数可以很方便的生成关于雷达点的Voronoi图，并返回相应节点的坐标位置［1］。

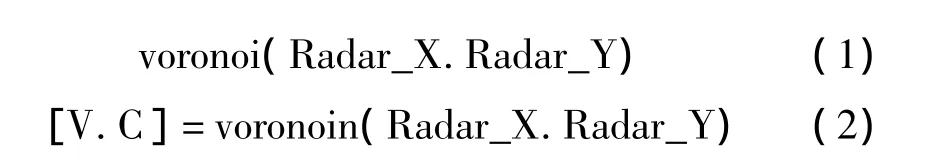
其中voronoi函数可作出Voronoi图，voronoin函数返回相应数据;Radar_X为11×1维矩阵，代表雷达点在该区域中位置的横坐标;Radar_Y为11×1维矩阵，代表雷达点在该区域中位置的纵坐标;返回值V为n×2维矩阵，代表Voronoi图垂直平分线交点在图中的坐标位置，n值由雷达的数量和雷达的位置决定;C为11×1维矩阵，代表相应雷达点对应的V向量中的节点下标。

图3 Voronoi图

图3为voronoi函数生成的Voronoi图，从图中可以看出每条线段即相邻两个雷达点的垂直平分线。无人机按照此线飞行即可以安全执行飞行任务。因此，采用Voronoi图生成的初始飞行路径就能够很好的回避危险区域，为之后的进一步路径优化提供了便利［2］。

2.2 利用Dijkstra算法筛选最短路径

要在 Matlab中实现 Dijkstra算法需要求得Voronoi图中节点对应的距离矩阵Distance_M［3］。对于无人机飞行路径的起点、终点与节点的连接方法，文中选择起点与终点分别和与此两点可连通的距离最近的节点对应的两雷达点的中点连接，利用式（2）中得到的矩阵C可以求得距离矩阵，如表1所示为所得距离矩阵部分数据。表中数值为inf表示两点不可连通，如Distance_M（1，3）=inf表示节点1和节点3无法连通，数值不为inf表示两点可连通，如Distance_M（1，2）=2.304 9表示节点1和节点2可连通并且其相距 2.304 9 km［4－5］。

表1 距离矩阵部分数据

利用距离矩阵Distance_M并结合Dijkstra算法即可求得基于Voronoi图所得节点的最短路径:

其中:distance表示返回经Dijkstra算法计算得到的最短路径长度;path为1×m维矩阵，表示最短路径从起点到终点的节点下标。所得路径如图4粗实线所示。

图4 利用Dijkstra算法得到的最短路径

2.3 利用分割法优化最短路径

由图4可以看出经过Voronoi图法和Dijkstra算法得到的路径在拐点处的曲率变化非常大，这就要求无人机在经过每个拐点时都要急剧改变控制角以改变飞行路径，这对于无人机来说是难以从技术上实现的。

文中提出采用分割法将图3中路径的每条线段进行等长分割，分割段数用section表示，定义Min_D为航迹到雷达点的最小距离，显然有:

依次连接起点与之后的分割点成一条直线，直到直线（无人机飞行路径）与圆（雷达扫描范围）的最小距离小于Min_D，即最短飞行路径所能达到的极限位置。此时记录下上一分割点，并以此分割点为新的起点依次连接此点以后的分割点。重复以上过程直到最后连接点为终点。如图5所示，图中虚线即section=50时，经过分割法得到的无人机飞行路径（考虑到无人机飞行的安全性，在此取Min_D=1.2）。

2.4 平滑优化路径

虽然经过分割法优化后得到的路径拐点减少，但是仍存在前后曲率变化过大的拐点。采用B样条函数对路径进行平滑可以很好的解决所得路径在曲率及保持原路径的一致性之间的矛盾。Matlab中的spcrv函数为生成均匀划分的B样条函数，利用spcrv函数对Dijkstra算法生成的路径进行均匀划分，即可得到平滑的飞行路径。如图6中曲线所示为经spcrv函数计算所得的路径，不仅能够保证偏离原路径的幅度较小，而且能够满足无人机安全飞行的要求。

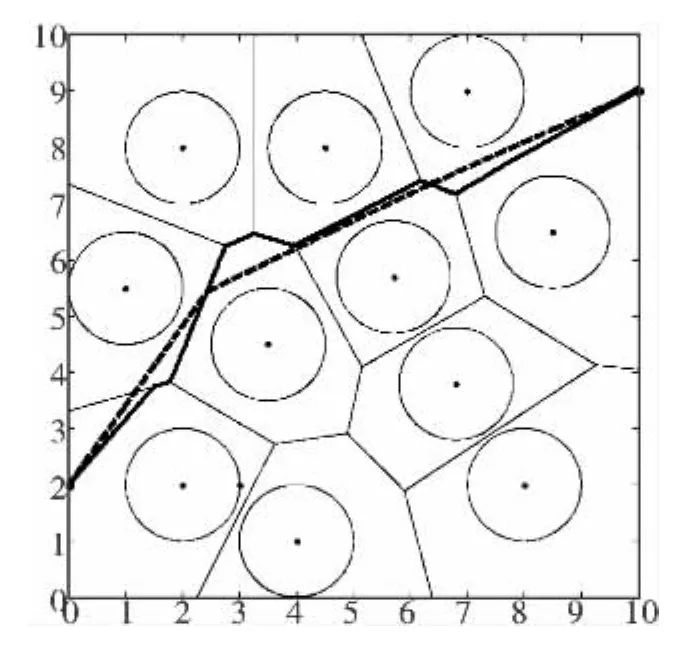
图5 利用分割法得到的优化路径

3 仿真结果

文中基于Voronoi图和Dijkstra算法得到无人机飞行的初始路径，利用分割法对所得路径进行优化以减少拐点，最后对所得路径进行平滑，得到满足约束条件的最优飞行路径。

3.1 section取值对所得路径影响

为了获知采用分割法时section的取值对所得无人机路径的影响，文中分别对section不同取值进行仿真实验。如图7中a、b、c、d依次为section取值为5，10，50，500时得到的路径。实验结果表明，当 section＜50时，随着section取值的增大，所得最优路径逐渐趋于平滑，改变明显。当section≥50时，所得的最优路径的改变不再明显。

图8所示为本次仿真section不同取值情况下所得路径的总路程，从图中可以看出，当section取值小于50时，所得最优路径的路程长度优化效果明显;当section取值大于500时，随着section的增大并不能明显降低最优路径的路程长度。

3.2 各阶段路程长度对比

如图9所示为某次仿真实验section取值为50时，所得路径长度依次经Dijkstra算法、分割法、spcrv平滑后所得数据，由图可以看出采用文中提出的分割法对经Dijkstra算法得到的路径进行优化，可以有效缩短飞行路径，经spcrv函数对路径进行平滑后，可进一步缩短飞行路径。

图7 section取值不同时的路径

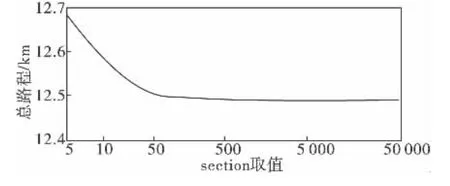
图8 总路程对比

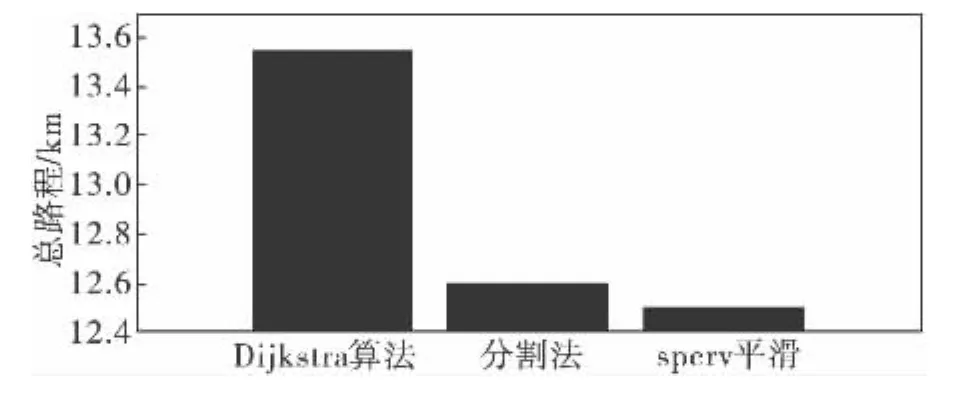
图9 各阶段总路程对比

3.3 计算时间对比

图10所示为section依次取值为5，10，50，500，5 000，50 000时，程序执行所需的时间。为了减少其他随机性因素对程序执行时间的影响，将section每种取值的情况都仿真10次并取平均值。从图中可以看出，当section取值小于50时，程序执行时间变化不大，均在0.379 3 s以内。当section取值大于5 000时，程序执行时间呈指数式增长。当section=50 000时，程序执行时间为14.718 5 s。

图10 计算时间对比

综合以上实验结果表明，当section取值在50左右时，所得最优路径的路程长度就可达到满意效果，并且计算所需时间非常短。在实际应用中，可根据需要在50左右对section取值。

4 结论

为解决无人机路径规划问题，文中在Matlab软件平台下，基于Voronoi图并结合Dijkstra算法得到初始飞行路径。利用文中提出的分割法对初始飞行路径进行优化可进一步减少初始路径中的拐点并缩短路径路程，最后利用spcrv函数对路径进行平滑得到能够满足无人机安全飞行要求的最优路径。仿真结果证明了文中算法的可行性，并且验证了其时间性能。在下一步的工作中，仍需对获取最优路径的算法做进一步的改良。

［1］张志涌。Matlab教程［M］.北京:北京航空航天大学出版社，2010.

［2］许松清，吴海彬，林宜，等.基于Voronoi图法的移动机器人路径规划［J］.中国工程机械学报，2005，3（3）:336－340.

［3］陈理荣.数学建模导论［M］.北京:北京邮电学院出版社，1999.

［4］DongKai Fan，Ping Shi.Improvement of Dijktra’s algorithm and its application in route planning［C］//2010 Seventh International Conference on Fuzzy Systems and Knowledge Discovery Vol.4，2010，4:1901 －1904.

［5］Yin Chao，Wang Hongxia.Developed Dijkstra shortest path search algorithm and simulation［C］//2010 International Conference on Computer Design and Applications Vol.1，2010:116－119.